NCERT Solutions for Class 9 Maths Chapter 4 Lines and Angles Ex 4.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 4 Lines and Angles Ex 4.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | Lines and Angles |
| Exercise | Ex 4.1 |
| Number of Questions Solved | 6 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 4 Lines and Angles Ex 4.1
Question 1.
In figure, lines AB and CD intersect at 0. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
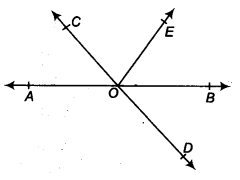
Solution:
Here, ∠AOC and ∠BOD are vertically opposite angles.
∴ ∠AOC = ∠BOD
⇒ ∠AOC = 40° [∵ ∠BOD = 40°(Given)] …(i)
We have, ∠AOC + ∠ BOE = 70° (Given)
40°+ ∠BOE = 70° [From Eq. (i)]
⇒ ∠BOE = 30°
Also, ∠AOC + ∠COE + ∠BOE = 180° (Linear pair axiom)
⇒ 40° + ∠COE + 30° = 180°
⇒ ∠COE = 110°
Now, ∠COE + reflex ∠COE = 360° (Angles at a point)
110°+reflex ∠COE = 360°
⇒ Reflex ∠COE = 250°
Question 2.
In figure, lines XY and MN intersect at 0. If ∠POY = 90° , and a : b = 2 : 3. find c.
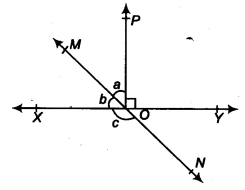
Solution:
We have, ∠POY = 90°
⇒ ∠POY + ∠POX = 180° (Linear pair axiom)
⇒ ∠POX = 90°
⇒ a+b = 90°
Also, a : b = 2 : 3 (Given)
⇒ Let a = 2k,b = 3k
Now, from Eq. (j), we get
2k + 3k = 90°
⇒ 5k = 90°
⇒ k = 18°
∴ a = 2 x 18°=36°
and b=3 x 18°=54°
Now, ∠MOX + ∠XON = 1800 (Linear pair axiom)
b+ c = 180°
⇒ 540 + c= 180°
⇒ c = 126°
Question 3.
In figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
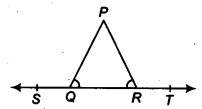
Solution:
∵ ∠PQS+ ∠PQR = 180° (Linear pair axiom) ,..(i)
and ∠PRT + ∠PRQ = 180° (Linear pair axiom).. .(ii)
From Eqs. (i) and (ii), we get
∠PQS + ∠PQR =∠PRT + ∠PRQ
∠PQS + ∠PRQ =∠PRT + ∠PRQ
[Given, ∠PQR = ∠PRQ]
⇒ ∠PQS = ∠PRT
Question 4.
In figure, if x + y = w + z, then prove that AOB is a line.
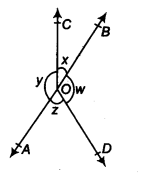
Solution:
∵ x+ y+w+ z = 360° (Angle at a point)
x + y = w + z (Given)…(i)
∴ x+ y+ x+ y = 360° [From Eq. (i)]
2(x + y) = 360°
⇒ x + y = 180° (Linear pair axiom)
Hence, AOB is a straight line.
Question 5.
In figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
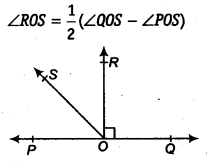
Solution:
We have,
∠POR = ∠ROQ = 90° (∵ Given that, OR is perpendicular to PQ)
∴ ∠POS + ∠ROS = 90°
⇒ ∠ROS = 90° – ∠POS
On adding ∠ROS both sides, we get
2 ∠ROS = 90° – ∠POS + ∠ROS
⇒ 2 ∠ROS = (90° + ∠ROS) – ∠POS
⇒ 2∠ROS = ∠QOS – ∠POS (∵ ∠QOS = ∠ROQ + ∠ROS = 90° + ∠ROS)
⇒ ∠ROS = \(\frac { 1 }{ 2 }\) (∠QOS – ∠POS)
Hence proved.
Question 6.
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
Solution:
Here, YQ bisects ∠ZYP.
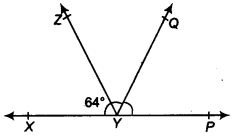
Hence, ∠ZYQ = ∠QYP = \(\frac { 1 }{ 2 }\) ∠ZYP ……..(i)
Given, ∠XYZ = 64° ….(ii)
∵ ∠XYZ + ∠ZYQ + ZQYP = 180° (Linear pair axiom)
⇒ 64° + ∠ZYQ + ∠ZYQ = 180° [From Eqs. (i) and (ii)]
⇒ 2 ∠ZYQ = 180° – 64°
⇒ ∠ZYQ = \(\frac { 1 }{ 2 }\) x 116°
⇒ ∠ZYQ = 58°
∴ ∠XYQ = ∠XYZ + ∠ZYQ = 64° + 58° = 122°
Now, ∠QYP + reflex ∠QYP = 360°
58° + reflex ∠QYP = 360°
⇒ reflex ∠ QYP = 302°
We hope the NCERT Solutions for Class 9 Maths Chapter 4 Lines and Angles Ex 4.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 4 Lines and Angles Ex 4.1, drop a comment below and we will get back to you at the earliest.