Tag: Reflection of Light

Reflection of Light

Light is a form of electromagnetic radiation that causes in us a sensation of sight. It also provides us means of communication through optical fiber cables. Several phenomena taking place in nature can be explained by understanding the nature and properties of light.

Reflection of light is the bouncing back of light rays in the same medium on striking a smooth and polished surface.

Laws of Reflection

The reflection of light from mirrors takes place according to the following laws of reflection:

1. The angle of incidence (i) is equal to the angle of reflection (r).
2. The incident ray, the reflected ray, and the normal to the mirror at the point of incidence, all lie on the same plane.

Types of Images

Real image: The image formed by the actual intersection of rays after reflection from the object and which can be obtained on a screen is called a real image.

Virtual image: The image formed if the rays of light after reflection from the object do not actually meet but appear to meet when produced backward and which cannot be obtained on a screen is called a virtual image.

Characteristics of Image Formed by a Plane Mirror

• Image formed by a plane mirror is virtual and erect.
• The image is of the same size as the object.
• It is formed as far behind the mirror as the object is in front of it.
• The image is laterally inverted (inverted sideways).

Spherical Mirror

A spherical mirror is a mirror whose reflecting surface is the part of a hollow sphere of glass. A concave mirror is the spherical mirror in which the reflecting surface is the concave or bent-in surface.
A convex mirror is a spherical mirror in which the reflecting surface is the convex or bulging-out surface.

Centre of curvature (C): It is the centre of the hollow sphere of glass of which the mirror is a part. It lies in front of a concave mirror and behind a convex mirror.

Radius of curvature(R): It is the radius of the hollow sphere of glass of which the mirror is part.

Pole (P): The centre of reflection surface of a spherical mirror.

Principal axis: It is the straight line passing through the centre of curvature and pole of a spherical mirror.

Aperture: It is the portion of a mirror from which the reflection of light actually takes place. It represents the size of the mirror. It is the diameter of the reflecting surface of spherical mirror.

Principal focus: The point on the principal axis of the mirror at which the rays of light incident on the mirror in a direction parallel to the principal axis meet after reflection (in case of concave mirror) or appear to diverge after reflection (in case of convex mirror). It is represented by the letter F.

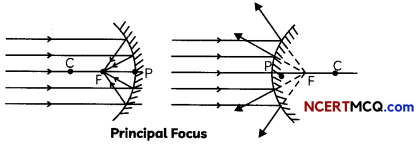
Relation between radius of curvature and focal length: The focal length of a spherical mirror is equal to half of its radius of curvature, i.e., f = R/2.

Image Formation by Spherical Mirrors

1. The ray parallel to the principal axis after reflec-tion passes through the principal focus F of a concave mirror or appears to pass through the principal focus of a convex mirror.

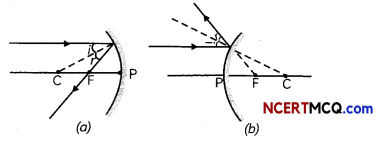
2. A ray passing through the principal focus of a con¬cave mirror or a ray which is directed towards the principal focus of convex mirror becomes parallel to the principal axis after reflection.

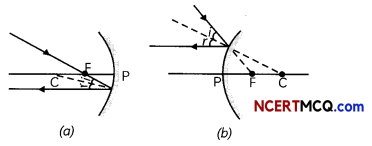
3. A ray passing through the centre of curvature of a concave mirror or directed towards the centre of curvature of convex mirror is reflected back along its own path. The light rays come back along the same path because the incident rays fall on the mirror along the normal to the reflecting surface.

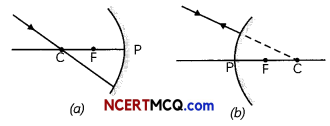
4. A ray incident obliquely to the principal axis at or a convex mirror reflected

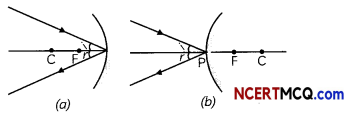
The image formed by a concave mirror: The nature, position and size of the image formed by a plane mirror depends on the position of the object in relation to points P, F and C.

Example 1.
We wish to obtain an erect image of an object, using a concave mirror of focal length 15 cm. What should be the range of distance of the object from the mirror? What is the nature of the image? Is the image larger or smaller than the object? Draw a ray diagram to show the image formation in this case.
Answer:
A concave mirror forms an erect image of an object when the object lies between the pole and focus of the mirror. As the focal length of the concave mirror = 15 cm, therefore, range of distance of the object from the mirror = 0 to less than 15 cm in front of the mirror.

The image formed will be virtual and larger than the object.

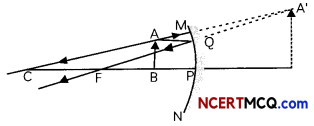
Uses of concave mirrors:

1. Concave mirror is used as a shaving mirror when the face is placed close to it so that it is within its focus and we get an erect and magnified image of the face.
2. Doctors use concave mirror as a head-mirror to concentrate parallel rays of light on its focus which enables them to examine such body parts as eye, throat etc.
3. Large concave mirrors are used to concentrate sunlight to produce heat in solar furnaces.
4. Concave mirrors are used in torches, search-lights and vehicles’ headlights to get powerful parallel beams of light.

Example 2.
Case Based:
In the first activity, take a convex mirror. Hold it in one hand. Hold a pencil in the upright position in the other hand. Observe the image of the pencil in the mirror. Now, move the pencil away from the mirror slowly and repeat this activity carefully.
In the second activity, observe the image of a distant object, say a distant tree, in a plane mirror. Try with plane mirrors of different sizes. Repeat this Activity with a concave mirror. Now try using a convex mirror.
(A) In the first activity, the image of the pencil in the mirror is:
(a) Erect and enlarged
(b) Erect and diminished
(c) Inverted and diminished
(d) Inverted and enlarged.
Answer:
(b) Erect and diminished

Explanation: The image of pencil obtained in the convex mirror is erect and diminished. This is because a convex mirror always forms a virtual, erect and diminished image of an object.

(B) Select the incorrect observation when the pencil is moved away from the mirror slowly:
(I) The image becomes smaller
(II) The image becomes larger
(III) The image moves from the pole towards the focus.
(IV) The image moves farther away from the focus.
(a) Both (I) and (III)
(b) Both (I) and (IV)
(c) Both (II) and (III)
(d) Both (II) and (IV)
Answer:
(d) Both (II) and (IV)

Explanation: As the object is moved slowly away from the convex mirror, the distance of the image of the pencil from the mirror increases i.e., the image shifts from the pole towards the focus and the size of image gradually decreases. When the object is at infinity (very far), the image is at its focus.

(C) Can full length image of a distant object be seen in a plane mirror?
Answer:
No, full length image of a distant object cannot be seen in a plane mirror.

Explanation: Image formed in a plane mirror is of the same size as the object and hence full length image of distant object, such as a tree, cannot be seen in a plane mirror.

(D) Can full length image of a distant object be obtained in a concave mirror?
Answer:
No, full length image of a distant object cannot be seen in a concave mirror.

Explanation: Image formed of a distant object in a concave mirror is diminished due to which we cannot see the full length image of a distant object in a concave mirror.

You can see a full-length image of a tall building/ tree in a small convex mirror. One such mirror is fitted in a wall of Agra Fort. If you visit the Agra Fort, try to observe the full-length image of a distant, tall building/tomb in the wall mirror. To view the tomb distinctly, you should stand suitably at the terrace adjoining the wall.

(E) Assertion (A): Full-length image of a distant object, such as a tall building, can be seen in a convex mir¬ror.
Reason (R): A convex mirror has a greater focal length than a concave mirror of the same aperture.
(a) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the (A).
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(c) (A) is true, but (R) is false.

Explanation: We can obtain Full Length image of a distant object, such as a tall building, can be seen in a convex mirror since a convex mirror always form a virtual and diminished image of an object. Moreover, convex mirror has a wider field of view due to which it is used as rear or side view mirrors in vehicles as distant objects in the backdrop can be seen clearly with much larger field of view.

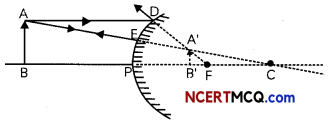
Image formed by a convex mirror: A convex mirror always forms virtual and diminished image of objects. The image formed by a convex mirror is much smaller than the object which gives the convex mirror a wider field of view.
The image formed by a convex mirror becomes smaller and smaller and will move closer to the focus as the object is moved away from the convex mirror.

Uses of convex mirrors:

1. Convex mirrors are used as rear-view mirrors in vehicles. These mirrors are fitted on the sides of the vehicles enabling the driver to see traffic behind him to facilitate safe driving as they give an erect and diminished image.
2. They have a wider field of view as they are curved outside and hence enable the driver to view much larger area.

Example 3.
No matter how far you stand from a mirror, your image appears erect. The mirror is likely to be
(a) plane.
(b) concave.
(c) convex.
(d) either plane or convex.
Answer:
(d) either plane or convex.

Explanation: Only plane mirror and convex mirror always form virtual and erect image of object, no matter what the position of the object is.

Reflection from a Concave Mirror

1. As the position of object shifts from infinity to focus F, the position of image shifts from focus F to Infinity and size of image increases from highly diminished to highly enlarged.

2. When the object is that the focus, the image is at infinity. As the object moves towards the mirror within the focal point the image becomes virtual and upright behind the mirror. Initially the virtual image is much larger than the object and really far away, but as the object approaches the mirror the virtual image also approaches the mirror and decreases in size.

Reflection from Convex Mirror

When the object is far away from the mirror the image is upright and located at the focal point. As the object approaches the mirror the image also approaches the mirror and grows until its height equals that of the object.

New Cartesian Sign Conventions for Reflection by Spherical Mirrors

1. The object is on the left of the mirror i.e., light is incident on the mirror from the left of the mirror.
2. All distances are measured from the pole of the mirror as the origin.
3. The distances measured in the direction of the incident light are taken as positive and distances measured in the direction opposite to the direction of incident light are taken as negative.
4. Distances measured upwards (above X-axis) and perpendicular to the principal axis is taken as positive and all distances measured downwards are taken as negative.

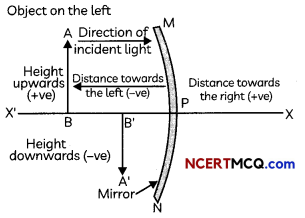
Important

• The object distance, u, is always negative.
• The image distance, v, is positive if the image is formed behind a concave mirror and negative if the image is formed in front of the mirror.
• The image distance, v, is always positive for a convex mirror.
• The focal length of a concave mirror is always negative and that of a convex mirror always positive.
• The height of an object is always positive.
• If the image is erect the height is taken as positive and if the image is inverted, the height is taken as negative.

Mirror Formula

The mirror formula gives a relation between the object distance (u), the image distance (v) and focal length (f) of a spherical mirror.
Mirror formula: \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)

Example 4.
The magnification produced by a plane mirror is +1. What does this mean?
Answer:
Magnification has two components: the sign denotes whether image is real (minus sign) or virtual (plus sign) and magnitude denotes the relative size of image as compared to the object.

As plane mirror always produces a virtual image, sign is plus. As size of image = size of object, magnitude is 1.
Therefore, magnification produced by a plane mirror is +1 indicates that image formed by a plane mirror is virtual and of same size as object.

Important

• The magnification in case of a convex mirror is always positive as it always forms a virtual image.
• The magnification in case of a concave mirror is positive for a virtual image and negative for a real image.

Example 5.
A concave mirror produces three times magnified (enlarged) real image of an object placed at 10 cm in front of it. Where is the image located?
Answer:
Magnification produced by a spherical mirror is
defined as m = \(\frac{\text { height of image }}{\text { height of object }}=-\frac{v}{u}\)
Here, m = – 3 (as image is three times magnified and real image).
u = -10 cm.
Therefore, m = \(-\frac{v}{u} \Rightarrow-3=-\frac{v}{-10} \Rightarrow\) v = -30 cm. u = -10
So, the image is located 30 cm in front of the concave mirror.

Class 10 Science Notes