Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.
The Integrated Rate Equation
We have just learnt that the rate of change of concentration of the reactant is directly proportional to that of concentration of the reactant. For a general reaction, A → product. The rate law is Rate = \(\frac{-d[A]}{dt}\) = k[A]x
Where k is the rate constant, and x is the order of the reaction. The above equation is a differential equation, \(\frac{-d[A]}{dt}\), so it gives rate at any instant. However, using the above expression, we cannot answer questions such as how long will it take for a specific concentration of A to be used up in the reaction? What will be the concentration of reactant after a time ‘t’?. To answer such questions, we need the integrated form of the above rate law which contains time as a variable.
Integrated Rate Law for a First Order Reaction
A reaction whose rate depends on the reactant concentration raised to the first power is called a first order reaction. Let us consider the following first order reaction,
A → Product
Rate law can be expressed as
Rate = k[A]1
Where, k is the fist order rate constant.
\(\frac{-d[A]}{dt}\) = k[A]1
⇒ \(\frac{-d[A]}{[A]}\) = k dt …………… (1)
Integrate the above equation between the limits of time t = 0 and time equal to t, while the concentration varies from the initial concentration [A0] to [A] at the later time.
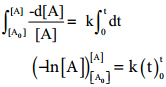
– ln[A] – (- In[A0]) = k (t-0)
– ln[A] + In[A0] = kt
ln(\(\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}\)) = kt ……….. (2)
This equation is in natural logarithm. To convert it into usual logarithm with base 10, we have to multiply the term by 2.303. 2.303 log (\(\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}\)) = kt
k = \(\frac{2.303}{t}\)log(\(\frac{\left[\mathrm{A}_{0}\right]}{[\mathrm{A}]}\)) ………… (3)
Equation (2) can be written in the form y = mx + c as below
ln[A0]-ln[A] = kt
ln[A] = ln[A0]-kt
⇒ y = c + mx
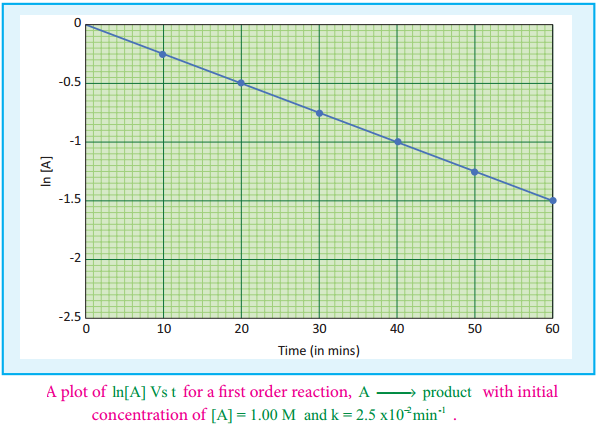
If we follow the reaction by measuring the concentration of the reactants at regular time interval ‘t’, a plot of ln[A] against ‘t’ yields a straight line with a negative slope. From this, the rate constant is calculated. Examples for the first order reaction
(i) Decomposition of Dinitrogen Pentoxide
N2O5(g) → 2NO2(g) + \(\frac{1}{2}\)O2(g)
(ii) Decomposition of Sulphurylchloride
SO2Cl2(l) → SO2(g) + Cl2(g)
(iii) Decomposition of the H2O2 in aqueous solution; H2O2 → H2O(l) + \(\frac{1}{2}\)O2(g)
(iv) Isomerisation of Cyclopropane to Propene.
Pseudo First Order Reaction:
Kinetic study of a higher order reaction is difficult to follow, for example, in a study of a second order reaction involving two different reactants; the simultaneous measurement of change in the concentration of both the reactants is very difficult.
To overcome such difficulties, A second order reaction can be altered to a first order reaction by taking one of the reactant in large excess, such reaction is called pseudo first order reaction. Let us consider the acid hydrolysis of an ester,
![]()
Rate = k [CH3COOCH3] [H2O]
If the reaction is carried out with the large excess of water, there is no significant change in the concentration of water during hydrolysis. i.e.,concentration of water remains almost a constant.
Now, we can define k [H2O] = k’; Therefore the above rate equation becomes
Rate = k'[CH3COOCH3]
Thus it follows first order kinetics.
Integrated Rate law for a Zero Order Reaction:
A reaction in which the rate is independent of the concentration of the reactant over a wide range of concentrations is called as zero order reactions. Such reactions are rare. Let us consider the following hypothetical zero order reaction.
A → product
The rate law can be written as,
Rate = k[A]°
\(\frac{-d[A]}{dt}\) = k(1) (∴[A]° = 1)
⇒ -d[A] = k dt
Integrate the above equation between the limits of [A°] at zero time and [A] at some later time ‘t’,
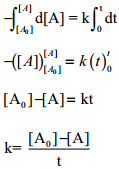
Equation (2) is in the form of a straight line y = mx + c
i.e., [A] = – kt + [A°]
⇒ y = c + mx
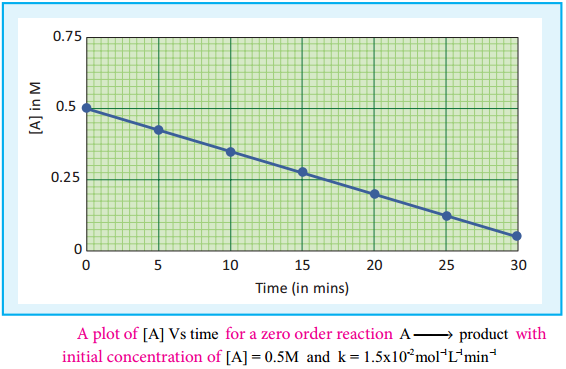
A plot of [A] Vs time gives a straight line with a slope of – k and y – intercept of [A°].
Fig 7.4: A plot of [A] Vs time for a zero order reaction A → product with initial concentration of [A] = 0.5M and k = 1.5 × 10-2mol-1L-1min-1
Examples for a Zero Order Reaction:
1. Photochemical reaction between H2 and I2
![]()
2. Decomposition of N2O on hot Platinum Surface
N2O(g) ⇄ N2(g) + \(\frac{1}{2}\)O2(g)
3. Iodination of Acetone in Acid Medium is Zero Order With Respect to Iodine.
![]()
Rate = k [CH3COCH3][H+]