Three Dimensional Geometry Class 12 Notes Maths Chapter 11

By going through these CBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry, students can recall all the concepts quickly.

Three Dimensional Geometry Notes Class 12 Maths Chapter 11

1. Direction cosines of a line:
Let AB be a line in space.
Through O, draw a line OP parallel to AB. Let OP makes angles α, β, and γ with OX, OY, and OZ respectively.

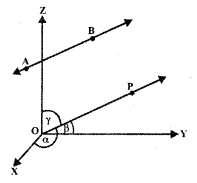
Cosines of the angles α, β, and γ,
i.e., cos α, cos β, and cos γ are known as the direction cosines of line AB.
Let l = cos α, m = cos β, n = cos γ
⇒ l, m, n are the direction cosines of the line AB Let us consider the ray BA. OQ is drawn parallel to BA. Now, OQ makes angles n – α, n – β, and n – γ with coordinates axes OX, OY, and OZ respectively.

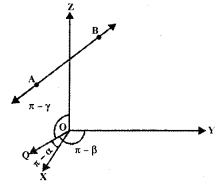
∴ Direction cosines of BA are cos(π – α), cos (π – β) and cos (π – γ),
i.e., – cos α, – cos β, – cos γ or -l, -m, -n.

→ Relation between l, m, and n
AB is any ray having direction cosines l, m, n. Now OP is drawn parallel to AB, where P is the point (x, y, z). Let PM be drawn perpendicular to OY.

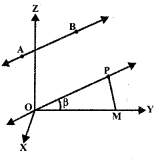
In ΔOPM OP = r (say). PM⊥OY.
∴ ∠PMO = 90°
Also, ∠POM = β.
∴ \(\frac{\mathrm{OM}}{\mathrm{OP}}\) = β
∴ \(\frac{y}{r}\) = m,
∴ y = rm

Similarly, x = rl and z = rn.
Now, OP² = x² + y² + z²
r² = (rl)² + (rm)² + (rn)²
or
r² = r²(l² + m² + n²)
⇒ l² + m² + n² = 1.

→ Direction Ratios of a line
Definition: The numbers which are proportional to the direction cosines of a line are known as direction ratios of the line.

Let Z, m, n be the direction cosines of a line.
Multiplying each by r, we ger rl, rm, rn the direction ratios.
Let rl = a,rm = b and rn – c.
Squaring and adding
r²l² + r²m² + r²n² = a² + b² + c²
∴ r²(l² + m² + n²) = a² + b² + c²
∵ l² + m² + n² = 1
∴ l = \(\frac{a}{r}=\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

Similarly, m = \(\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}\) and n = \(\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

Thus, if a, b and c are the direction ratios of a line, the direction cosines are \(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}\), \(\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}\) and \(\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\).

→ Direction cosines of the line passing through the points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂)
Direction ratios of the line PQ are x₂ – x₁, y₂ – y_1, z₂ – z₁
∴ PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)
∴Direction cosines of PQ are \(\frac{x_{2}-x_{1}}{\mathrm{PQ}}\), \(\frac{y_{2}-y_{1}}{\mathrm{PQ}}\), \(\frac{z_{2}-z_{1}}{P Q}\)

2. Angle between the two lines
1. Let l_1, m₁, n₁, and l₂, m₂, n₂ be the direction cosines of the lines OP and OQ.

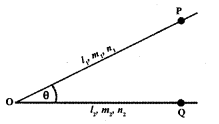
The angle θ between these lines is given by
cos θ = l₁l₂ + m₁m₂ + n₁n₂
and sin θ = \(\sqrt{\left(m_{1} n_{2}-m_{2} n_{1}\right)^{2}+\left(n_{1} l_{2}-n_{2} l_{1}\right)^{2}+\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}\)

2. If a₁, b₁, c₁ and a₂, b₂, c₂ are the direction ratios of two lines, then

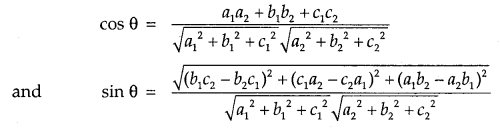
3. Two lines are perpendicular to each other,
if θ = \(\frac{π}{2}\) ⇒ cos θ = cos \(\frac{π}{2}\) = 0
⇒ l₁l₂ + m₁m₂ + n₁n₂ = 0
or
a₁a₂ + b₁b₂ + c₁c₂ = 0

4. When the lines are parallel
θ = 0 ⇒ sin θ = sin 0 = 0.

STRAIGHT LINE
3. Equation of a line through a given point:
(a) Let the line passes through \(\vec{a}\) and is parallel to vector \(\vec{b}\)

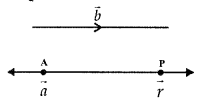
Then, the equation of the line is
\(\vec{r}\) – \(\vec{a}\) = λ\(\vec{b}\)
or
\(\vec{r}\) = \(\vec{a}\) + λ\(\vec{b}\)

(b) Let the point A be (x₁, y₁, z₁) and a, b, c are the direction ratios of the line. The equation of the line is
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)
If l, m, n are the direction cosines, then equation of the line is
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=\frac{z-z_{1}}{n}\)

4. Equation of the line passing through two points:
(a) Let \(\vec{a}_{1}\), \(\vec{a}_{2}\) be the position vectors of two points P and Q respectively.
⇒ \(\vec{b}\) = \(\vec{a}_{1}\) – \(\vec{a}_{2}\)

∴ Equation of PQ is
\(\vec{r}\) = \(\vec{a}\) + λ(\(\vec{a}_{2}\) – \(\vec{a}_{1}\))

(b) Direction ratios of the line passing through P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) are x₂ – x₁, y₂ – y₁ and z₂ – z₁
∴ Equation of the line PQ is
\(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)

5. Angle between two straight lines:

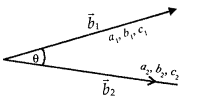
(a) Let the two lines be
\(\vec{r}\) = \(\vec{a}_{1}\) + λ\(\vec{b}_{1}\)
\(\vec{r}\) = \(\vec{a}_{2}\) + λ\(\vec{b}_{2}\)
If θ be the angle between them, then
cos θ = \(\frac{\vec{b}_{1} \vec{b}_{2}}{\left|\vec{b}_{1}\right|\left|\vec{b}_{2}\right|}\)

(b) Let the lines be
\(\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}\)
and \(\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}\)
i.e., a1, b1, c1 and a2, b2, c2 are the direction ratios of the lines.
∴ cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)
If l1, m1, n1 and l₂, m₂, n₂ are the direction cosines, then
cos θ = l₁l₂ + m1m₂ +n1n₂

6. Shortest Distance:
(a)Let \(\vec{r}\) = \(\vec{a}_{1}\) + λ\(\vec{b}_{1}\) and
\(\vec{r}\) = \(\vec{a}_{2}\) + λ\(\vec{b}_{2}\) be the two non-intersecting lines.
The shortest distance between the given lines = \(\left|\frac{\left(\vec{b}_{1} \times \vec{b}_{2}\right) \cdot\left(\vec{a}_{2}-\vec{a}_{1}\right)}{\left|\vec{b}_{1} \times \vec{b}_{2}\right|}\right|\)

(b) Let the lines be

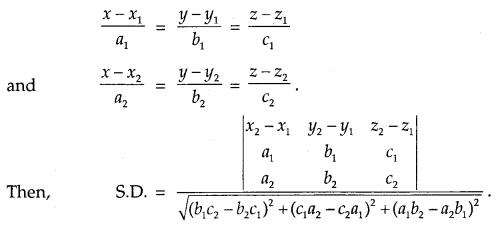
If the lines are intersecting, then lines are coplanar.
⇒ S.D. = 0
⇒ (\(\vec{b}_{1} \times \vec{b}_{2}\)) – (\(\vec{a}_{1} \times \vec{a}_{2}\)) = 0
or
\(\left|\begin{array}{ccc}
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2}
\end{array}\right|\) = 0

7. Distance between parallel lines:
Let the parallel lines be
\(\vec{r}\) = \(\vec{a}_{1}\) + λ\(\vec{b}_{1}\) and
\(\vec{r}\) = \(\vec{a}_{2}\) + μ\(\vec{b}_{2}\)

Shortest distance d between these lines is given by,
d = \(\left|\frac{\vec{b} \times\left(\vec{a}_{1}-\vec{a}_{2}\right)}{|\vec{b}|}\right|\)

PLANES
8. Different forms of equations of a plane:
1. Normal Form.
(a) Let the plane ABC be at a distance d from the origin. ON is the normal to the plane in the directon n̂. Equation of the plane is \(\vec{r}\). n̂ = d.

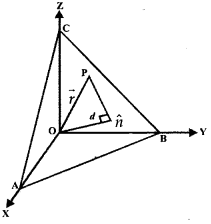
(b) If l, m, n are the direction cosines of the normal to the plane which is at distance d from the origin. The equation of the plane is lx + my + nz = d.
However, general form of the equation of a plane are \(\vec{r}\) .\(\overrightarrow{\mathrm{N}}\) = D and Ax + By + Cz + D = 0.

2. (a) Let the plane passes through a point A and let it perpendicular to the vector \(\overrightarrow{\mathrm{N}}\)
∴ Equation of the plane
(\(\vec{r}\) – \(\vec{a}\)).\(\overrightarrow{\mathrm{N}}\) = 0.

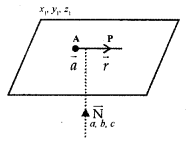
(b) If a plane passes through (x₁, y₁, z₁) and perpendicular to the line with direction ratios a, b, c the equation of the plane is
a(x – x₁) + b(y – y₁)+c(z – z₁) =0

3. Equation of the plane passing through three points.
(a) Let the three points be A, B and C whose position vectors be, \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\)
The equation of the plane is
\((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]\) = 0

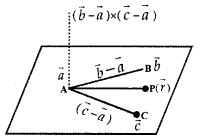
(b) Let the three points through which the plane is passing be A(x₁, y₁, z₁), B(x₂, y₂, z₂), and C(x₃, y₃, z₃).
Then, equation of the plane is
\(\left|\begin{array}{llll}
x & y & z & 1 \\
x_{1} & y_{1} & z_{1} & 1 \\
x_{2} & y_{2} & z_{2} & 1 \\
x_{3} & y_{3} & z_{3} & 1
\end{array}\right|\) = 0
or
\(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|\) = 0

4. Intercepts form of the equation of the plane
Let the plane make the intercepts a, b, and c on coordinate axes OX, OY, and OZ respectively.

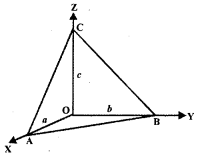
Then, the equation of the plane is
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1

9. Plane passing through the intersection of the two planes:
Let the equation of two planes be
\(\vec{r}\). \(\vec{n}_{1}\) = d1 and
\(\vec{r}\) .\(\vec{n}_{2}\) = d2

The equation of the plane passing through the line of intersection of the given planes is
(\(\vec{r}\). \(\vec{n}_{1}\) – d1) + λ(\(\vec{r}\) .\(\vec{n}_{2}\) – d2) = 0
or
\(\vec{r}\) .(\(\vec{n}_{1}\) + λ\(\vec{n}_{2}\)) = (d1 + λd2)

(b) Equation of the plane passing through the line of intersection of the planes
a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is (a₁x + b₁ y + c₁z + d₁ + λ(a₂x + b₂y + c₂z + d₂) = 0
or
(a₁ + λa₂)x + (b₁ + λb₂)y + (c₁ + λc₂)z + d₁ + λd₂ = 0,
where λ is determined according to the given condition.

10. Coplanarity of two lines:

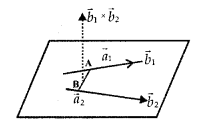
(a) The two lines
\(\vec{r}\) = \(\vec{a}_{1}\) + λ\(\vec{b}_{1}\) and
\(\vec{r}\) = \(\vec{a}_{2}\) + λ\(\vec{b}_{2}\) intersect each other, if \(\left(\vec{a}_{2}-\vec{a}_{1}\right) \cdot\left(\vec{b}_{2} \times \vec{b}_{1}\right)\) = 0

11. The angle between the planes:
Definition : The angle between the two planes is the angle between their normals. The angle 0 between the planes
\(\vec{r}\) = \(\vec{n}_{1}\) = d1 and \(\vec{r}\) = \(\vec{n}_{1}\) = d2 is given by cos θ = \(\frac{\left|\vec{n}_{1} \cdot \vec{n}_{2}\right|}{\left|\vec{n}_{1}\right|\left|\vec{n}_{2}\right|}\)

(b) If the planes are
a₁x + b₁y + C₁z + d₁ = 0
a₂x + b₂y + c₂z + d₂ = 0, then the angle θ between these planes is given by
cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)

(c) The planes are perpendicular to each other, if θ = \(\frac{π}{2}\)
∴ cos \(\frac{π}{2}\) = 0 ⇒ \(\vec{n}_{1}\).\(\vec{n}_{2}\) = 0
or
a₁a₂ + b₁b₂ + c₁c₂ = 0

(d) The planes a₁x + b₁y +c₁z + d₁ = 0
and a₂x + b₂y + c₂z + d₂ = O
are parallel, if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\).

(e) Equation of the plane parallel to
\(\vec{r} \cdot \vec{n}\) = d is \(\vec{r} \cdot \vec{n}\) = λ
Plane parallel to
ax + by + cz + d = 0 is ax + by + cz + λ = 0.

12. Distance of a point from th plane:
(a) Let the plane be \(\vec{r} \cdot \vec{n}\) = d.
∴ Perpendicular distance of the point \(\vec{a}\) from the plane
=|d – \(\vec{a} \cdot \hat{n}\)|

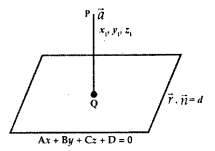
(b) Let the equation of the plane
be Ax + By + Cz + D= O.
The distance of the point (x1, y1, z1) from this plane
= \(\left|\frac{A x_{1}+B y_{1}+C z_{1}+D}{\sqrt{A^{2}+B^{2}+C^{2}}}\right|\)

13. Angle between a line and a plane:
Definition: The angle between a line and plane is said to be the complement of the angle between the line and the normal to the plane.

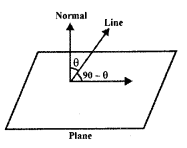
(a) Let the line and plane be
\(\vec{r}\) = \(\vec{a}\) + λ\(\vec{b}\) and \(\vec{r} \cdot \vec{n}\) = d.

If θ be the angle between the plane and the line, then
sin θ = \(\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\)

(b) ¡et the line and the plane be \(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\) and Ax + By + Cz + D = O.
The angle Φ between them is given by
sin Φ = \(\frac{a \cdot \mathrm{A}+b \cdot \mathrm{B}+c \cdot \mathrm{C}}{\sqrt{a^{2}+b^{2}+c^{2}} \sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}+\mathrm{C}^{2}}}\).

1. IMPORTANT RESULT

l² + m² + n² = 1, where < l, m, n > are direction-cosines of a st. line.

2. DIRECTION-RATIOS

The direction-ratios of the line joining of the points (x₁, y₁, z₁) and (x₂, y₂, z₂) are :
<x₂-x₁, y₂-y₁ ,z₂-z₁ >.

3. (i) Angle between two lines. The angle between two lines having direction-cosines
< l₁ m₁ n₁ > and < l₂, m₂, n₂ > is given by :
cos θ = |l₁l₂+ m₁m₂ + n₁n₂|.

(ii) The lines are:
(a) perpendicular l₁l₂+ m₁m₂ + n₁n₂ = 0.
(b) parallel iff l₁ = l_2, m₁ = m₂, + n₁ = n₂ 

4. SHORTEST DISTANCE

The shortest distance between two lines :
\(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}} \text { and } \vec{r}=\overrightarrow{a_{2}}+\mu \overrightarrow{b_{2}} \text { is }\left|\frac{\left(\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right) \cdot\left(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}\right)}{\left|\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right|}\right|\)

5. EQUATIONS OF PLANES

(i) Equation of a plane, which is at a distance ‘p’ from the origin and perpendicular to the unit
vector \(\hat{n}\) is \(\vec{r} \cdot \hat{n}=p\)

(ii) General Form. The general equation of first degree i.e.ax + by + cz + d- 0 represents a plane,

(iii) One-point Form. The equation of a plane through (*,, y,, z,) and having <a,b,c> as direction-
ratios of the normal is a (x – x₁) + b (y – y₁) + c (z – z₁) = 0.

(iv) Three-point Form. The equation of the plane through (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) is:
\(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x-x_{2} & y-y_{2} & z-z_{2} \\
x-x_{3} & y-y_{3} & z-z_{3}
\end{array}\right|=0\)

(v) Intercept Form. Equation of the plane, which cuts off intercepts a, b, c on the axes, is :
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1

6. ANGLE BETWEEN TW O PLANES
The angle between the planes :
a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is given by :
cos θ = \(\frac{\left|a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)

7. BISECTING PLANES
The equations of the planes bisecting the planes :
a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are:
\(\frac{a_{1} x+b_{1} y+c_{1} z+d_{1}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}=\pm \frac{a_{2} x+b_{2} y+c_{2} z+d_{2}}{\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)