
On this page, you will find Triangles Class 10 Notes Maths Chapter 6 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 6 Triangles will seemingly help them to revise the important concepts in less time.
CBSE Class 10 Maths Chapter 6 Notes Triangles
Triangles Class 10 Notes Understanding the Lesson
In X standard we have learnt about congruent figures.
Congruent figure: Those two geometric figures having the same shape and size are known as congruent figures.
Rules of Congruency
1. SAS (Side-Angle-Side): Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
2. ASA (Angle-Side-Angle): Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
3. AAS (Angle-Angle-Side): Two triangles are Congruent if any two pairs of angles and a pair of corresponding sides are equal.
4. SSS (Side-Side-Side): If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
5. RHS (Right angle-Hypotenuse-Side: In two right angle triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Note: All congruent figures or triangles are similar.
Similar Figure: Two figure which are of same shape (but not necessarily the same size) are called similar figures. For example,
- All line segments are similar.
- All circles are similar.
- Two or more squares are similar.
- Two or more equilateral triangles are similar.
Note:
- All rectangles are not similar.
- All triangles are not similar.
Similar Polygons: Two polygons with the same number of sides are similar, if (1) their corresponding angles are equal. (2) their corresponding sides in the same ratio.
Similarity of Triangles
Two triangles are similar if
- Their corresponding angles are equal; and
- Their corresponding sides are in the same ratio
Famous Greek mathematician Militus Thales gives the relation to the two equiangular triangle is known as BPT or Thales theorem.
Equiangular triangles: If corresponding angles of two triangles are equal then they are equiangular triangles
Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Given: A AABC in which a line DE || BC intersects the other two sides AB and AC at D and E respectively.
To Prove that \(\frac{A D}{D B}=\frac{A E}{E C}\)
Construction: Join BE and CD and draw DM ⊥ AC and EN ⊥ AB
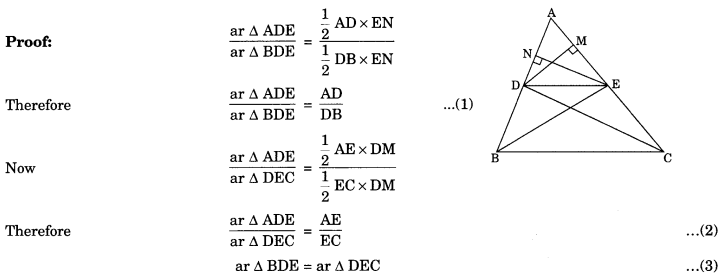
(Because both are on the same base DE and between the same parallels BC and DE) from eqn (1), (2) and (3) AD AE

Theorem 6.2: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
AD AE Given: In ΔABC, \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
To prove: DE || BC
Construction: Let us suppose that DE is not parallel to BC, so we draw a line DF || BC
Proof: DF || BC
Therefore by Basic Proportionality Theorem,

which is not possible. We come at the contradiction. So our supposition was wrong, it is only possible, if point F will coincide the point E.
Therefore DE || BC.
Criteria for Similarity of Triangles
In previous section, we have studied that two triangles are similar, if (I) their corresponding angles are similar (II) their corresponding sides are proportional (or are in the same ratio).
Theorem 6.3: AAA Criterion: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
In ΔABC and ΔDEF,

Remark : AA Similarity Creterian: If two angles of a triangle are equal to two angles of another triangle, then their corresponding angles are equal and the triangles are similar.
In ΔABC and ΔDEF
∠A =∠D, ∠C = ∠F then ΔABC ~ ΔDEF (by AA similarity)
Theorem 6.4: SSS Similarity Criterion: If the corresponding sides of two triangles are proportional (i.e. in the same ratio), then their corresponding angles are equal and the triangles are similar.
In ΔABC and ΔDEF
\(\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F} DF \)then ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
Hence ΔABC ~ ΔDEF
Theorem 6.5: SAS Similarity Criterion: If one angle of a triangle is equal to one angle of the other and the sides including these angles are proportional, the triangles are similar.
In ΔABC and ΔDEF
∠BAC = ∠EDF
\(\frac{A B}{D E}=\frac{A C}{D F}\)
Hence ΔABC ~ ΔDEF
Areas of Similar Triangles
We have study in two similar triangles. Ratio of the corresponding sides of two similar triangles is same.
Theorem 6.6: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given: ΔABC ~ ΔPQR
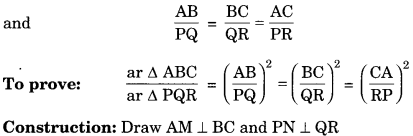
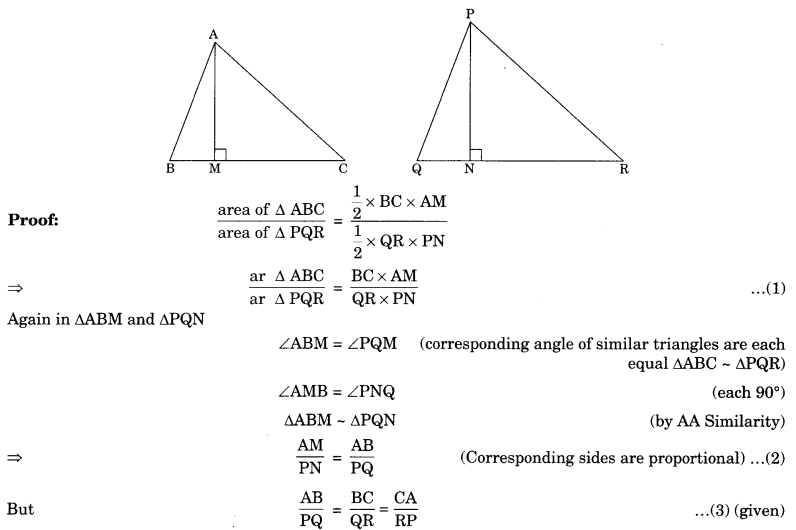

Theorem 6.7: If a perpendicular is drawn from the verities of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
- ΔADB ~ ΔABC
- ΔBDC ~ ΔABC
- ΔADB ~ ΔBDC
Theorem 6.8: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: ABC is a right angle triangle which is right angled at B.
To prove: AC2 = AB2 + BC2
Construction: Draw BD ⊥ AC
Proof: ΔADB ~ ΔABC
(If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other)
From equation (2) and (3)
Adding eqn (1) and (2)
(If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse than triangles on both sides of the perpendicular are similar to the whole triangle and to each other)
AB2 + BC2 = AD . AC + CD . AC
⇒ AB2 + BC2 = AC (AD + CD)
⇒ AB2 + BC2 = AC x AC
⇒ AB2 + BC2 = AC2
⇒ AC2 = AB2 + BC2
Theorem 6.9: In a triangle, if square of one side is equal to the sum of the squares of the other two sides. Then the angle opposite the first side is a right angle.
Given: We have ΔABC in which
AC2 = AB2 + BC2
To prove: ∠ABC = 90°
Construction: Construct a ΔDEF right angled at E such that EF = BC and DE = AB
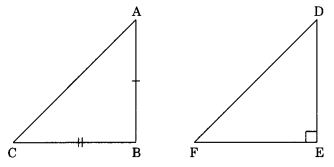
Proof: In ΔDEF
DF2 = EF2 + DE2 (Pythagoras theorem) (given)
DF2 = BC2 + AB2…(1) (by construction)
But AC2 = BC2 + AB2…(2)
From eqn (1) and (2)
AC2 = DF2
⇒ AC = DF… (3)
In ΔABC and ΔDEF
AB = DE(by construction)
BC = EF(by construction)
AC = DF(proved above in eqn (3))
ΔABC ≅ ΔDEF(by SSS congruence)
⇒ ∠ABC = ∠DEF (by CPCT)
Therefore ∠ABC = 90°