Here we are providing Triangles Class 9 Extra Questions Maths Chapter 7 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-9-maths/
Extra Questions for Class 9 Maths Triangles with Answers Solutions
Extra Questions for Class 9 Maths Chapter 7 Triangles with Solutions Answers
Triangles Class 9 Extra Questions Very Short Answer Type
Triangles Class 9 Extra Questions Question 1.
Find the measure of each exterior angle of an equilateral triangle.
Solution:
We know that each interior angle of an equilateral triangle is 60°.
∴ Each exterior angle = 180° – 60° = 120°
Class 9 Triangles Extra Questions Question 2.
If in ∆ABC, ∠A = ∠B + ∠C, then write the shape of the given triangle.
Solution:
Here, ∠A = ∠B + ∠C
And in ∆ABC, by angle sum property, we have
∠A + ∠B + C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
Hence, the given triangle is a right triangle.
Triangles Extra Questions Class 9 Question 3.
In ∆PQR, PQ = QR and ∠R = 50°, then find the measure of ∠Q.
Solution:
Here, in ∆PQR, PQ = QR
⇒ ∠R = ∠P = 50° (given)
Now, ∠P + ∠Q + ∠R = 180°
50° + ∠Q + 50° = 180°
⇒ ∠Q = 180° – 50° – 50°
= 80°
Class 9 Maths Chapter 7 Extra Questions With Solutions Question 4.
If ∆SKY ≅ ∆MON by SSS congruence rule, then write three equalities of corresponding angles.
Solution:
Since ∆SKY ≅ ∆MON by SSS congruence rule, then three equalities of corresponding angles
are ∠S = ∠M, ∠K = ∠O and ∠Y = ∠N.
Triangles Class 9 Extra Questions With Solutions Pdf Question 5.
Is ∆ABC possible, if AB = 6 cm, BC = 4 cm and AC = 1.5 cm ?
Solution:
Since 4 + 1.5 = 5.5 ≠ 6
Thus, triangle is not possible.
Triangle Class 9 Extra Questions Question 6.
In ∆MNO, if ∠N = 90°, then write the longest side.
Solution:
We know that, side opposite to the largest angle is longest.
∴ Longest side = MO.
Extra Questions On Triangles Class 9 Question 7.
In ∆ABC, if AB = AC and ∠B = 70°, find ∠A.
Solution:
Here, in ∆ABC AB = AC ∠C = ∠B [∠s opp. to equal sides of a ∆)
Now, ∠A + ∠B + ∠C = 180°
⇒ ∠A + 70° + 70° = 180° [∵ ∠B = 70°]
⇒ ∠A = 180° – 70° – 70° = 40°
Class 9 Maths Triangles Extra Questions Question 8.
In ∆ABC, if AD is a median, then show that AB + AC > 2AD.
Solution:
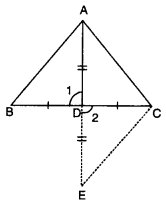
Produce AD to E, such that AD = DE.
In ∆ADB and ∆EDC, we have
BD = CD, AD = DE and ∠1 = ∠2
∆ADB ≅ ∆EDC
AB = CE
Now, in ∆AEC, we have
AC + CE > AE
AC + AB > AD + DE
AB + AC > 2AD [∵ AD = DE]
Triangles Class 9 Extra Questions Short Answer Type 1
Extra Questions On Congruence Of Triangles Class 9 Question 1.
In the given figure, AD = BC and BD = AC, prove that ∠DAB = ∠CBA.
Solution:
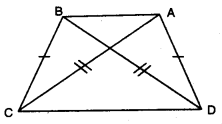
In ∆DAB and ∆CBA, we have
AD = BC [given]
BD = AC [given]
AB = AB [common]
∴ ∆DAB ≅ ∆CBA [by SSS congruence axiom]
Thus, ∠DAB =∠CBA [c.p.c.t.]
Extra Questions Of Triangles Class 9 Question 2.
In the given figure, ∆ABD and ABCD are isosceles triangles on the same base BD. Prove that ∠ABC = ∠ADC.
Solution:
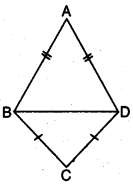
In ∆ABD, we have
AB = AD (given)
∠ABD = ∠ADB [angles opposite to equal sides are equal] …(i)
In ∆BCD, we have
CB = CD
⇒ ∠CBD = ∠CDB [angles opposite to equal sides are equal] … (ii)
Adding (i) and (ii), we have
∠ABD + ∠CBD = ∠ADB + ∠CDB
⇒ ∠ABC = ∠ADC
Extra Questions For Class 9 Maths Triangles Question 3.
In the given figure, if ∠1 = ∠2 and ∠3 = ∠4, then prove that BC = CD.
Solution:
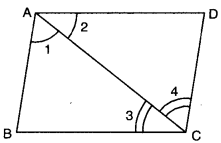
In ∆ABC and ACDA, we have
∠1 = ∠2 (given)
AC = AC [common]
∠3 = ∠4 [given]
So, by using ASA congruence axiom
∆ABC ≅ ∆CDA
Since corresponding parts of congruent triangles are equal
∴ BC = CD
Class 9 Maths Chapter 7 Extra Questions Question 4.
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.
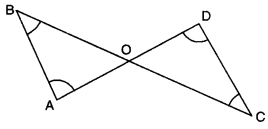
Solution:
Here, ∠B < ∠A
⇒ AO < BO …..(i)
and ∠C < ∠D
⇒ OD < CO …..(ii)
[∴ side opposite to greater angle is longer]
Adding (i) and (ii), we obtain
AO + OD < BO + CO
AD < BC
Triangles Class 9 Important Questions With Solutions Question 5.
In the given figure, AC > AB and D is a point on AC such that AB = AD. Show that BC > CD.
Solution:
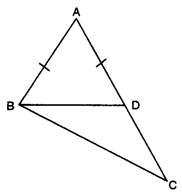
Here, in ∆ABD, AB = AD
∠ABD = ∠ADB
[∠s opp. to equal sides of a ∆]
In ∆BAD
ext. ∠BDC = ∠BAD + ∠ABD
⇒ ∠BDC > ∠ABD ….(ii)
Also, in ∆BDC .
ext. ∠ADB > ∠CBD …(iii)
From (ii) and (iii), we have
∠BDC > CD [∵ sides opp. to greater angle is larger]
Class 9 Maths Ch 7 Extra Questions Question 6.
In a triangle ABC, D is the mid-point of side AC such that BD = \(\frac{1}{2}\) AC. Show that ∠ABC is a right angle.
Solution:
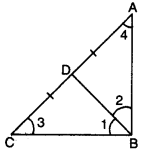
Here, in ∆ABC, D is the mid-point of AC.
⇒ AD = CD = \(\frac{1}{2}\)AC …(i)
Also, BD = \(\frac{1}{2}\)AC… (ii) [given]
From (i) and (ii), we obtain
AD = BD and CD = BD
⇒ ∠2 = ∠4 and ∠1 = ∠3 …..(iii)
In ∆ABC, we have
∠ABC + ∠ACB + ∠CAB = 180°
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180°
⇒ ∠1 + ∠2 + ∠1 + ∠2 = 180° [using (iii)]
⇒ 2(∠1 + ∠2) = 180°
⇒ ∠1 + ∠2 = 90°
Hence, ∠ABC = 90°
Triangles Class 9 Extra Questions Short Answer Type 2
Chapter 7 Maths Class 9 Extra Questions Question 1.
ABC is an isosceles triangle with AB = AC. P and Q are points on AB and AC respectively such that AP = AQ. Prove that CP = BQ.
Solution:
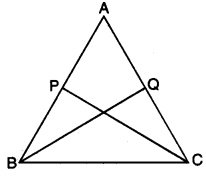
In ∆ABQ and ∆ACP, we have
AB = AC (given)
∠BAQ = ∠CAP [common]
AQ = AP (given)
∴ By SAS congruence criteria, we have
∆ABQ ≅ ∆ACP
CP = BQ
Questions On Triangles For Class 9 Question 2.
In the given figure, ∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC, AD is extended to intersect BC at P. Show that : (i) ∆ABD ≅ ∆ACD (ii) ∆ABP ≅ ∆ACP
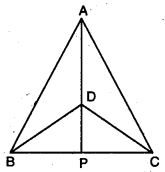
Solution:
(i) In ∆ABD and ∆ACD
AB = AC [given]
BD = CD [given]
AD = AD [common)]
∴ By SSS congruence axiom, we have
∆ABD ≅ ∆ACD
(ii) In ∆ABP and ∆ACP
AB = AC [given]
∠BAP = ∠CAP [c.p.cit. as ∆ABD ≅ ∆ACD]
AP = AP [common]
∴ By SAS congruence axiom, we have
∆ABP ≅ ∆ACP
Ch 7 Maths Class 9 Extra Questions Question 3.
In the given figure, it is given that AE = AD and BD = CE. Prove that ∆AEB ≅ ∆ADC.
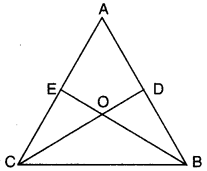
Solution:
We have AE = AD … (i)
and CE = BD … (ii)
On adding (i) and (ii),
we have AE + CE = AD + BD
⇒ AC = AB
Now, in ∆AEB and ∆ADC,
we have AE = AD [given]
AB = AC [proved above]
∠A = ∠A [common]
∴ By SAS congruence axiom, we have
∆AEB = ∆ADC
Triangles Class 9 Extra Questions With Solutions Question 4.
In the given figure, in ∆ABC, ∠B = 30°, ∠C = 65° and the bisector of ∠A meets BC in X. Arrange AX, BX and CX in ascending order of magnitude.
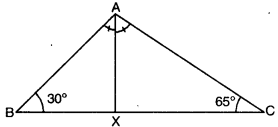
Solution:
Here, AX bisects ∠BAC.
∴ ∠BAX = ∠CAX = x (say)
Now, ∠A + ∠B + C = 180° [angle sum property of a triangle]
⇒ 2x + 30° + 65° = 180°
⇒ 2x + 95 = 180°
⇒ 2x = 180° – 95°
⇒ 2x = 85°
⇒ x = \(\frac{85^{\circ}}{2}\) = 42.59
In ∆ABX, we have x > 30°
BAX > ∠ABX
⇒ BX > AX (side opp. to larger angle is greater)
⇒ AX < BX
Also, in ∆ACX, we have 65° > x
⇒ ∠ACX > ∠CAX
⇒ AX > CX [side opp. to larger angle is greater]
⇒ CX > AX … (ii)
Hence, from (i) and (ii), we have
CX < AX < BX
Question 5.
In figure, ‘S’ is any point on the side QR of APQR. Prove that PQ + QR + RP > 2PS.
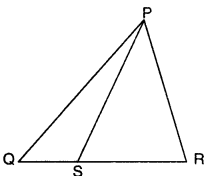
Solution:
In ∆PQS, we have
PQ + QS > PS …(i)
[∵ sum of any two sides of a triangle is greater than the third side]
In ∆PRS, we have
RP + RS > PS …(ii)
Adding (i) and (ii), we have
PQ + (QS + RS) + RP > 2PS
Hence, PQ + QR + RP > 2PS. [∵ QS + RS = QR]
Question 6.
If two isosceles triangles have a common base, prove that the line joining their vertices bisects them at right angles.
Solution:
Here, two triangles ABC and BDC having the common
base BC, such that AB = AC and DB = DC.
Now, in ∆ABD and ∆ACD
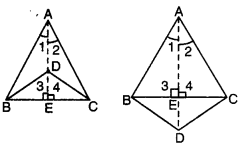
AB = AC [given]
BD = CD [given]
AD = AD [common]
∴ ΔABD ≅ ΔΑCD [by SSS congruence axiom]
⇒ ∠1 = ∠2 [c.p.c.t.]
Again, in ∆ABE and ∆ACE, we have
AB = AC [given]
∠1 = ∠2 [proved above]
AE = AE [common]
∆ABE = ∆ACE [by SAS congruence axiom]
BE = CE [c.p.c.t.]
and ∠3 = ∠4 [c.p.c.t.]
But ∠3 + ∠4 = 180° [a linear pair]
⇒ ∠3 = ∠4 = 90°
Hence, AD bisects BC at right angles.
Triangles Class 9 Extra Questions Long Answer Type
Question 1.
In the given figure, AP and DP are bisectors of two adjacent angles A and D of quadrilateral ABCD. Prove that 2 ∠APD = ∠B + 2C.
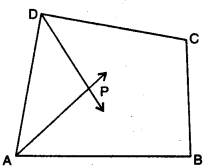
Solution:
Here, AP and DP are angle bisectors of ∠A and ∠D
∴ ∠DAP = \(\frac{1}{2}\)∠DAB and ∠ADP = \(\frac{1}{2}\)∠ADC ……(i)
In ∆APD, ∠APD + ∠DAP + ∠ADP = 180°
⇒ ∠APD + \(\frac{1}{2}\) ∠DAB + \(\frac{1}{2}\)∠ADC = 180°
⇒ ∠APD = 180° – \(\frac{1}{2}\)(∠DAB + ∠ADC)
⇒ 2∠APD = 360° – (∠DAB + ∠ADC) ……(ii)
Also, ∠A + ∠B + C + ∠D = 360°
∠B + 2C = 360° – (∠A + ∠D)
∠B + C = 360° – (∠DAB + ∠ADC) ……(iii)
From (ii) and (iii), we obtain
2∠APD = ∠B + ∠C
Question 2.
In figure, ABCD is a square and EF is parallel to diagonal BD and EM = FM. Prove that
(i) DF = BE (i) AM bisects ∠BAD.
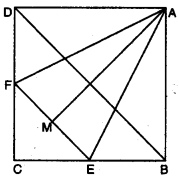
Solution:
(i) EF || BD = ∠1 = ∠2 and ∠3 = ∠4 [corresponding ∠s]
Also, ∠2 = ∠4
⇒ ∠1 = ∠3
⇒ CE = CF (sides opp. to equals ∠s of a ∆]
∴ DF = BE [∵ BC – CE = CD – CF)
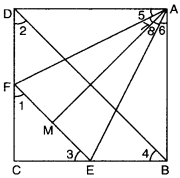
(ii) In ∆ADF and ∆ABE, we have
AD = AB [sides of a square]
DF = BE [proved above]
∠D = ∠B = 90°
⇒ ∆ADF ≅ ∆ABE [by SAS congruence axiom]
⇒ AF = AE and ∠5 = ∠6 … (i) [c.p.c.t.]
In ∆AMF and ∆AME
AF = AE [proved above]
AM = AM [common]
FM = EM (given)
∴ ∆AMF ≅ ∆AME [by SSS congruence axiom]
∴ ∠7 = ∠8 …(ii) [c.p.c.t.]
Adding (i) and (ii), we have
∠5 + ∠7 = ∠6 + ∠8
∠DAM = ∠BAM
∴ AM bisects ∠BAD.
Question 3.
In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that : (i) ∆AMC ≅ ∆BMD (ii) ∠DBC = 90° (ii) ∆DBC ≅ ∆ACB (iv) CM = \(\frac{1}{2}\)AB
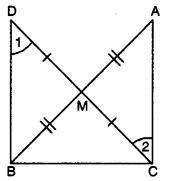
Solution:
Given : ∆ACB in which 4C = 90° and M is the mid-point of AB.
To Prove :
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC = 90°
(iii) ∆DBC ≅ ∆ACB
(iv) CM = \(\frac{1}{2}\)AB
Proof : Consider ∆AMC and ∆BMD,
we have AM = BM [given]
CM = DM [by construction]
∠AMC = ∠BMD [vertically opposite angles]
∴ ∆AMC ≅ ∆BMD [by SAS congruence axiom]
⇒ AC = DB …(i) [by c.p.c.t.]
and ∠1 = ∠2 [by c.p.c.t.]
But ∠1 and ∠2 are alternate angles.
⇒ BD || CA
Now, BD || CA and BC is transversal.
∴ ∠ACB + ∠CBD = 180°
⇒ 90° + CBD = 180°
⇒ ∠CBD = 90°
In ∆DBC and ∆ACB,
we have CB = BC [common]
DB = AC [using (i)]
∠CBD = ∠BCA
∴ ∆DBC ≅ ∆ACB
⇒ DC = AB
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)DC
⇒ \(\frac{1}{2}\)AB = CM or CM = \(\frac{1}{2}\)AB (∵ CM = \(\frac{1}{2}\)DC)
Question 4.
In figure, ABC is an isosceles triangle with AB = AC. D is a point in the interior of ∆ABC such that ∠BCD = ∠CBD. Prove that AD bisects ∠BAC of ∆ABC.
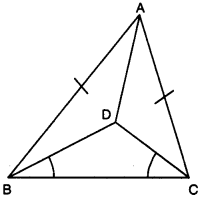
Solution:
In ∆BDC, we have ∠DBC = ∠DCB (given).
⇒ CD = BD (sides opp. to equal ∠s of ∆DBC)
Now, in ∆ABD and ∆ACD,
we have AB = AC [given]
BD = CD [proved above]
AD = AD [common]
∴ By using SSS congruence axiom, we obtain
∆ABD ≅ ∆ACD
⇒ ∠BAD = ∠CAD [c.p.ç.t.]
Hence, AD bisects ∠BAC of ∆ABC.
Question 5.
Prove that two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side of the other triangle.
Solution:
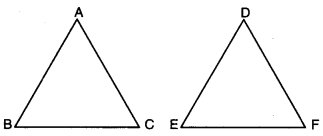
Given : Two As ABC and DEF in which
∠B = ∠E,
∠C = ∠F and BC = EF
To Prove : ∆ABC = ∆DEF
Proof : We have three possibilities
Case I. If AB = DE,
we have AB = DE,
∠B = ∠E and BC = EF.
So, by SAS congruence axiom, we have ∆ABC ≅ ∆DEF
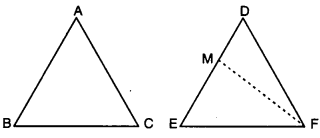
Case II. If AB < ED, then take a point Mon ED
such that EM = AB.
Join MF.
Now, in ∆ABC and ∆MEF,
we have
AB = ME, ∠B = ∠E and BC = EF.
So, by SAS congruence axiom,
we have ΔΑΒC ≅ ΔΜEF
⇒ ∠ACB = ∠MFE
But ∠ACB = ∠DFE
∴ ∠MFE = ∠DFE
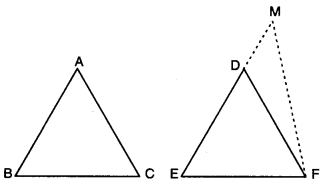
Which is possible only when FM coincides with B FD i.e., M coincides with D.
Thus, AB = DE
∴ In ∆ABC and ∆DEF, we have
AB = DE,
∠B = ∠E and BC = EF
So, by SAS congruence axiom, we have
∆ABC ≅ ∆DEF
Case III. When AB > ED
Take a point M on ED produced
such that EM = AB.
Join MF
Proceeding as in Case II, we can prove that
∆ABC = ∆DEF
Hence, in all cases, we have
∆ABC = ∆DEF.
Question 6.
In the given figure, side QR is produced to the point S. If the bisectors of ∠PQR and ∠PRS meet at T,
prove that ∠QTR = \(\frac{1}{2}\) ∠QPR.
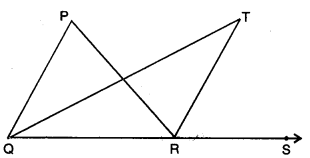
Solution:
Here, QT is angle bisector of ∠PQR
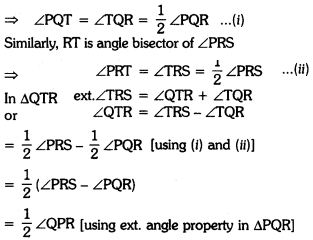
Triangles Class 9 Extra Questions HOTS
Question 1.
Show that the difference of any two sides of a triangle is less than the third side.
Solution:
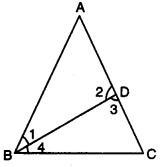
Consider a triangle ABC
To Prove :
(i) AC – AB < BC
(ii) BC – AC < AB
(iii) BC – AB < AC
Construction : Take a point D on AC
such that AD = AB.
Join BD.
Proof : In ∆ABD, we have ∠3 > ∠1 …(i)
[∵ exterior ∠ is greater than each of interior opposite angle in a ∆]
Similarly, in ∆BCD, we have
∠2 > ∠4 …..(ii) [∵ ext. ∠ is greater then interior opp. angle in a ∆]
In ∆ABD, we have
AD = AB [by construction]
∠1 = ∠2 …(iii) [angles opp. to equal sides are equal in a triangle]
From (i), (ii) and (iii), we have
⇒ ∠3 > ∠4 =
⇒ BC > CD
⇒ CD < BC
AC – AD < BC
AC – AB < BC [∵ AD = AB]
Hence, AC – AB < BC
Similarly, we can prove
BC – AC < AB
and BC – AB < AC
Question 2.
In the figure, O is the interior point of ∆ABC. BO meets AC at D. Show that OB + OC < AB + AC.
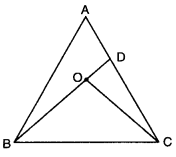
Solution:
In ∆ABD, AB + AD > BD …(i)
∵ The sum of any two sides of a triangle is greater than the third side. Also, we have
BD = BO + OD
AB + AD > BO + OD ….(ii)
Similarly, in ∆COD, we have
OD + DC > OC … (iii)
On adding (ii) and (iii), we have
AB + AD + OD + DC > BO + OD + OC
⇒ AB + AD + DC > BO + OC
⇒ AB + AC > OB + OC
or OB + OC < AB + AC
Hence, proved.
Triangles Class 9 Extra Questions Value Based (VBQs)
Question 1.
A campaign is started by volunteers of mathematical club to boost school and its surrounding under Swachh Bharat Abhiyan. They made their own logo for this campaign. What values are acquired by mathematical club ?
If it is given that ∆ABC ≅ ∆ECD, BC = AE.
Prove that ∆ABC ≅ ∆CEA.
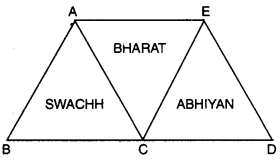
Solution:
Here, it is given that
∆ABC ≅ ∆ECD
AB = CE [c.p.c.t.]
BC = CD [c.p.c.t.]
AC = ED [c.p.c.t.]
Now, in ∆ABC and ∆CEA
BC = AE [given]
AB = EC [proved above]
AC = AC [common]
∴ By using SSS congruence axiom, we have
∆ABC ≅ ∆CEA
Value : Cleanliness and social concerning.
Question 2.
Rajiv, a good student and actively involved in applying knowledge A of mathematics in daily life. He asked his classmate Rahul to make triangle as shown by choosing one of the vertex as common. Rahul tried but not correctly. After sometime Rajiv hinted Rahul about congruency of triangle. Now, Rahul fixed vertex C as common vertex and locate point D, E such that AC = CD and BC = CE. Was the triangle made by Rahul is congruent ? Write the condition satisfying congruence.
What value is depicted by Rajiv’s action?
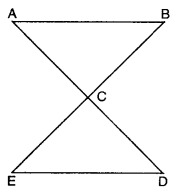
Solution:
In ∆ABC and ∆DEC, we have
AC = DC [by construction]
BC = EC [by construction]
∠ACB = ∠ECD [vert. opp. ∠s]
By using SAS congruence axiom, we have
∆ABC ≅ ∆DEC
Value : Cooperative learning, use of concept and friendly nature.
