Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity (With Applications to Maps and Models) Ex 15E

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E

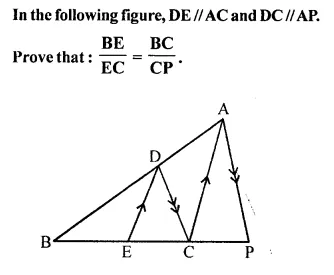
Question 1.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

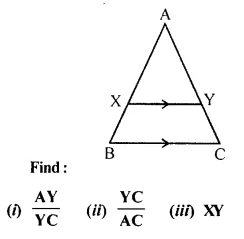
Solution:
In the given figure,

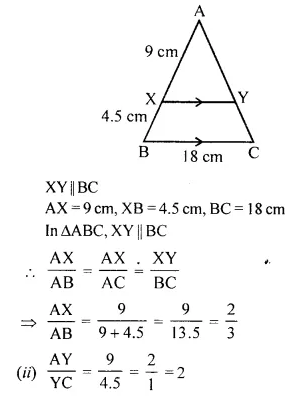
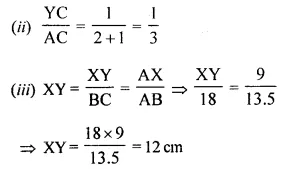
Question 2.
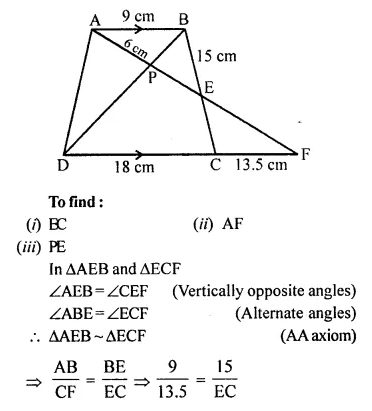
In the following figure, ABCD to a trapezium with AB // DC. If AB = 9 cm, DC = 18 cm, CF= 13.5 cm, AP = 6 cm and BE = 15 cm. Calculate:
(i) EC
(ii) AF
(iii) PE

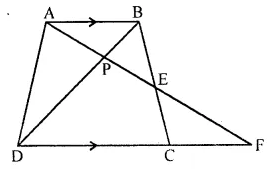
Solution:
In the figure,
ABCD is a trapezium
AB || DC
AB = 9 cm, DC = 18 cm, CF = 13.5 cm AP = 6 cm and BE = 15 cm

Question 3.
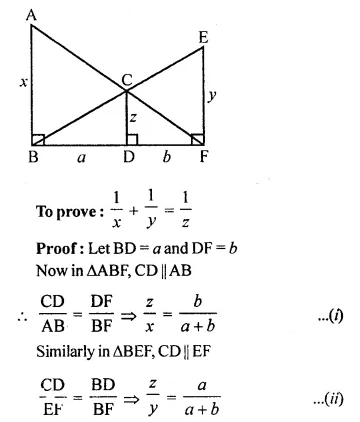
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.

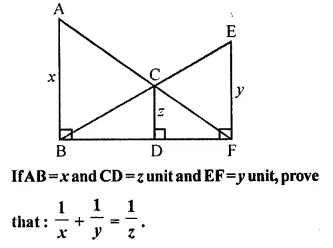
Solution:
In the given figure,
AB, CD and EF are perpendicular to the line BDF
AB = x, CD = z, EF = y

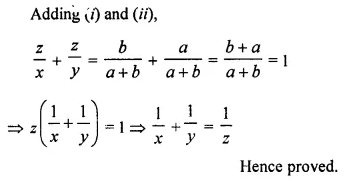
Question 4.
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that:
\(\frac { AB }{ PQ }\) = \(\frac { AD }{ PM }\)
Solution:
∆ABC ~ ∆PQR
AD and PM are the medians of ∆ABC and ∆PQR respectively.

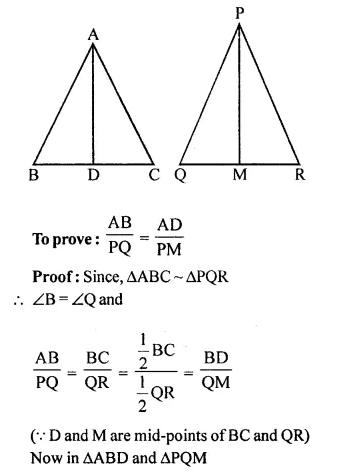
Question 5.
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that: \(\frac { AB }{ PQ }\) = \(\frac { AD }{ PM }\).
Solution:
Given, ∆ABC ~ ∆PQR
AD and PM are altitude of these two triangles

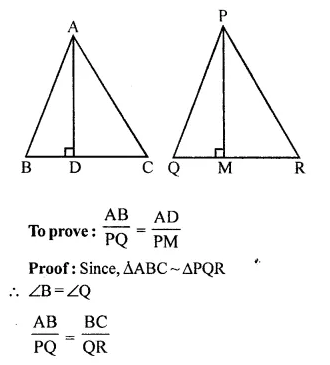
Question 6.
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that: \(\frac { AB }{ PQ }\) = \(\frac { AD }{ PM }\)
Solution:
Given, ∆ABC ~ ∆PQR
AD and PM are the angle bisectors of ∠A and ∠P respectively.

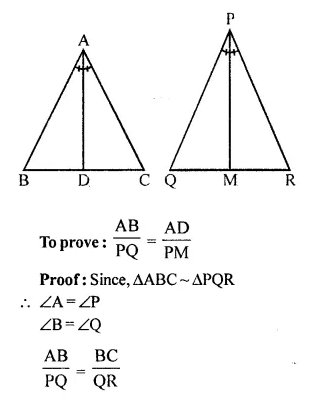
Question 7.

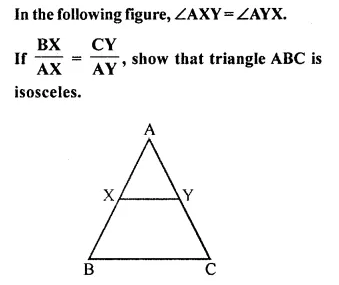
Solution:


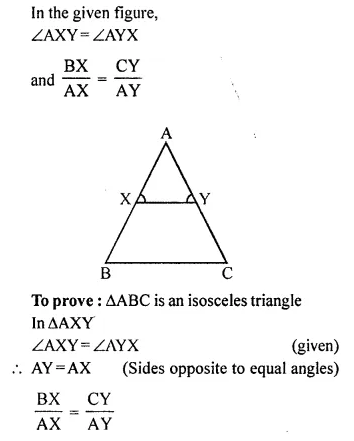
But ∠AXY = ∠AYX is given
∠B = ∠C
AC = AB (Side opposite to equal angles)
∆ABC is an isosceles triangle.

Question 8.
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.

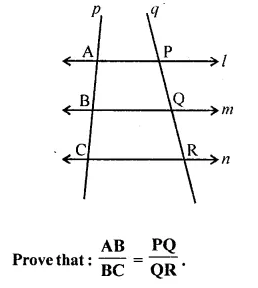
Solution:
In the given figure,
l || m || n
Transversal p and q intersects them at A, B, C and P, Q, R respectively as shown in the given figure.

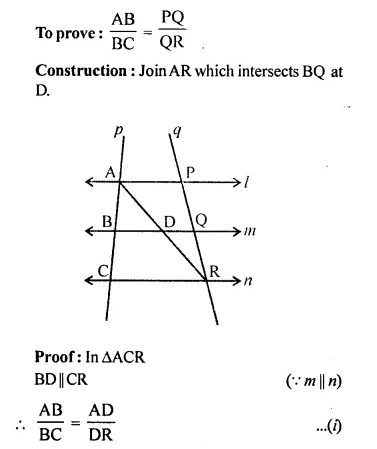
Question 9.

Solution:

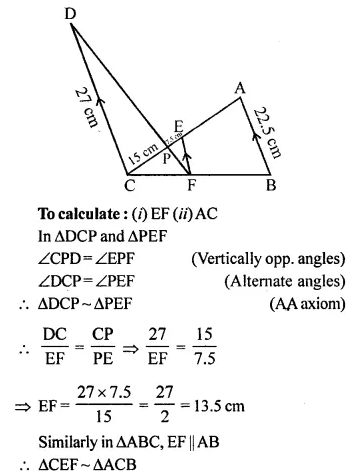
Question 10.
In the figure given below, AB // EF // CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate:
(i) EF
(ii) AC

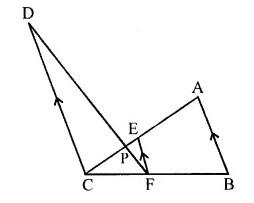
Solution:
In the given figure,
AB || EF || CD
AB = 22.5 cm, EP = 7.5 cm
PC = 15 cm and DC = 27 cm

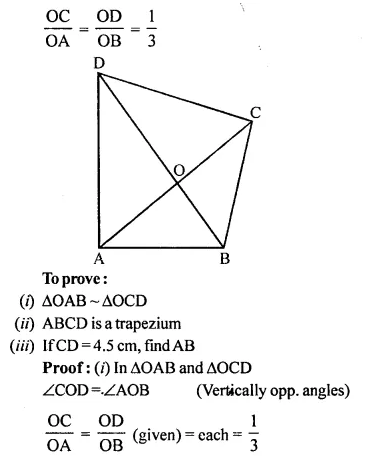
Question 11.
In quadrilateral ABCD, its diagonals AC and BD intersect at point O such that
\(\frac { OC }{ OA }\) = \(\frac { OD }{ OB }\) = \(\frac { 1 }{ 3 }\)
Prove that:
(i) ∆OAB ~ ∆OCD
(ii) ABCD is a trapezium.
Further if CD = 4.5 cm; find the length of AB.
Solution:
In quadrilateral ABCD, diagonals AC and BD intersect each other at O and

Question 12.
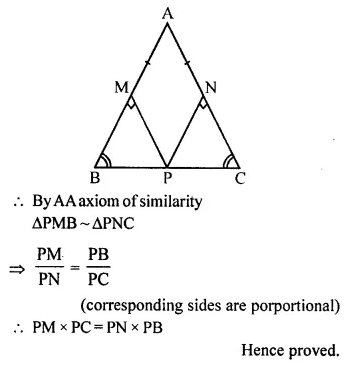
In triangle ABC, angle A is obtuse and AB = AC. P is any point in side BC. PM ⊥ AB and PN x AC.
Prove that: PM x PC = PN x PB
Solution:
Given, AB = AC
Since equal sides has equal angle opposite to it
∠B = ∠C …(i)
In ∆PMB and ∆PNC, we have
∠B = ∠C [using (i)]
∠PMB = ∠PNC (each 90°)

Question 13.
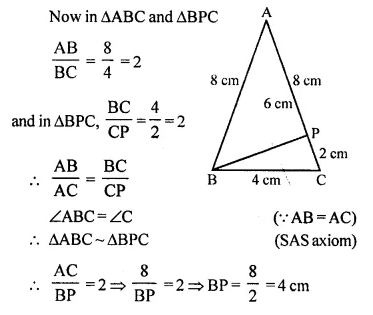
In triangle ABC, AB = AC = 8 cm, BC = 4 cm and P is a point in side AC such that AP = 6 cm. Prove that ∆BPC is similar to ∆ABC. Also, find the length of BP.
Solution:
In ∆ABC,
AB = AC = 8 cm
BC = 4cm
P is a point on AC such that AP = 6 cm
PB and PC are joined
To prove: ∆BPC ~ ∆ABC
and find length of BP
Proof: AC = 8 cm and AP = 6 cm
PC = AC – AP = 8 – 6 = 2 cm

Question 14.
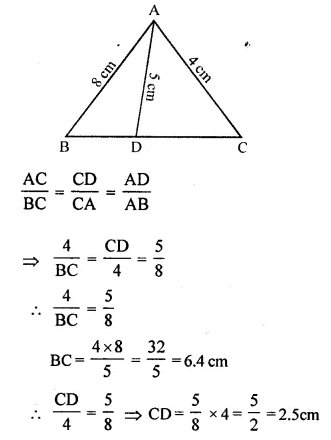
In ∆ABC, ∠ABC = ∠DAC. AB = 8 cm, AC = 4 cm, AD = 5 cm.
(i) Prove that ∆ACD is similar to ∆BCA.
(ii) Find BC and CD.
(iii) Find area of ∆ACD : area of ∆ABC. (2014)
Solution:
In ∆ACD and ∆BCA
∠C = ∠C (common)
∠ABC = ∠CAD (Given)
∆ACD = ∆BCA (by AA axiom)

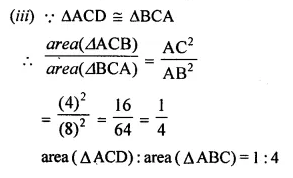
Question 15.
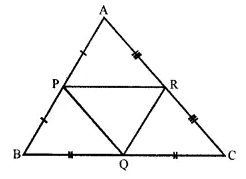
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

Solution:
Given : P and R the mid points of AB and AC respectively.
PR || BC and PR = \(\frac { 1 }{ 2 }\) BC = BQ.
PRQB is a || gm.
∠B = ∠PRQ ….(i)
Similarly, Q and R are the mid points of sides. BC and AC respectively
RQ || AB and QR = \(\frac { 1 }{ 2 }\) AB = AP
APQR is a ||gm.
∠A = ∠PQR ….(ii)
Similarly, we can prove that ∠C = ∠RPQ.
Now in ∆PQR and ∆ABC,
∠PQR = ∠A , ∠PRQ = ∠B and ∠RPQ = ∠C
(i) In ∆BCE
D is mid-point of BC and DF || CE
∆PQR ~ ∆ABC (AAA criterion of similarity)

Question 16.
In the following figure, AD and CE are medians of A ABC. DF is drawn parallel to CE. Prove that:
(i) EF = FB
(ii) AG : GD = 2 : 1

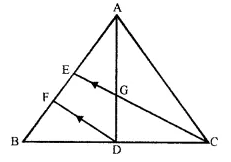
Solution:
Proof:
(i) In ∆BCE
D is the mid point of BC and DF || CE
E is mid-point of BE and EF = FB
(ii) AE = EB (E is mid point of AB)
and EF = FB (Proved)

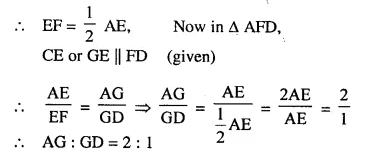
Question 17.
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.

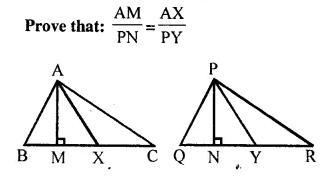
Solution:

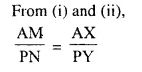
Question 18.
The two similar triangles are equal in area. Prove that the triangles are congruent.
Solution:
Given : ∆ABC ~ ∆PQR and are equal in area

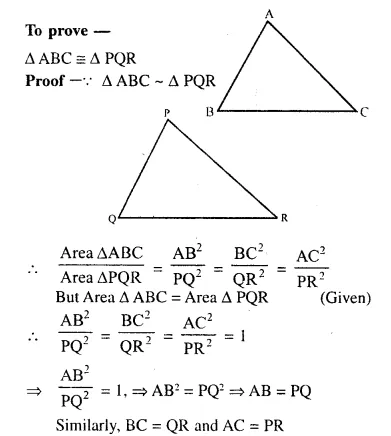
Question 19.
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their:
(i) medians
(ii) perimeters
(iii) areas
Solution:
∆ABC ~ ∆PQR
AL ⊥ BC and PM ⊥ QR

Question 20.
The ratio between the areas of two similar triangles is 16 : 25. Find the ratio between their:
(i) perimeters
(ii) altitudes
(iii) medians.
Solution:
∆ABC ~ ∆DEF,
AL ⊥ BC and DM ⊥ EF
and AP and DQ are the medians and also
area ∆ABC : area ∆DEF = 16 : 25

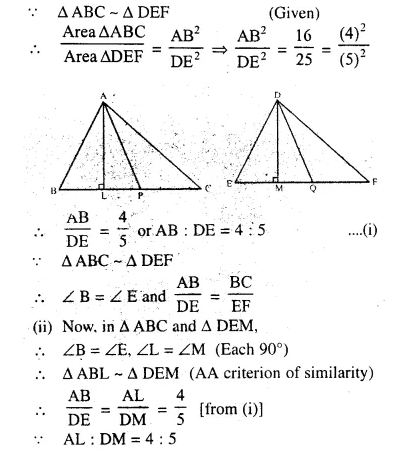
Question 21.
The following figure shows a triangle PQR in which XY is parallel to QR. If PX : XQ = 1 : 3 and QR = 9 cm, find the length of XY. Further, if the area of ∆PXY = x cm²; find in terms of x, the area of :
(i) triangle PQR.
(ii) trapezium XQRY.

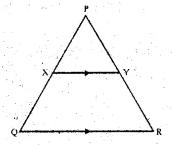
Solution:
In ∆PQR, XY || QR and PX : XQ = 1 : 3, QR = 9 cm.

Question 22.
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm, and BC = 32 cm. Calculate :
(i) The diagonal distance of the plot in kilometre
(ii) The area of the plot in sq. km.
Solution:

Question 23.
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50,. find the actual dimensions of the building. Also, find :
(i) the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq cm.
(ii) the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
Solution:
The scale factor is 1 : 50 or k = \(\frac { 1 }{ 50 }\)
Dimension of the building = 100 cm x 60 cm x 120 cm.
k x actual dimensions of the building = Dimension of the model.

Question 24.
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:
(i) ∆PQL ~ ∆RPM
(ii) QL x RM = PL x PM
(iii) PQ² = QR x QL [2003]

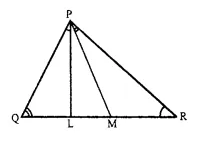
Solution:
(i) In ∆PQL and ∆RPM
∠PQL = ∠RPM (Given)
∠LPQ = ∠MRP (Given)
∆PQL ~ ∆RPM (AA criterion of similarity)
(ii) ∆PQL ~ ∆RPM (Proved)

Question 25.

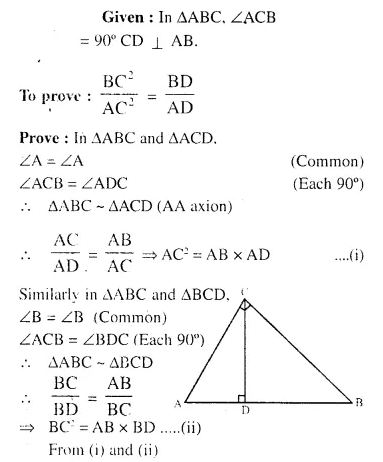
Solution:

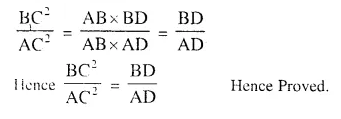
Question 26.
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ∆DEF such that the longest side of ∆DEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ∆DEF.
Solution:
In ∆ABC.
AB = 3 cm. BC = 6 cm and AC = 4 cm
In ∆DEF,
Longest side EF = 9 cm
and longest side in ∆ABC is BC = 6 cm

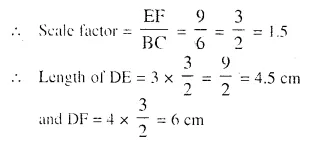
Question 27.
Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
Solution:
Let in two ∆ABC and ∆DEF
The vertical angles of two isosceles triangles are equal i.e. ∠A = ∠D
But AB = DE and AC = DF (isosceles ∆s)
Then base angles are also equal (Angles opposite to equal sides)
The two triangles are similar.
∆ABC ~ ∆DEF
Let AL ⊥ BC and DM ⊥ EF

Question 28.
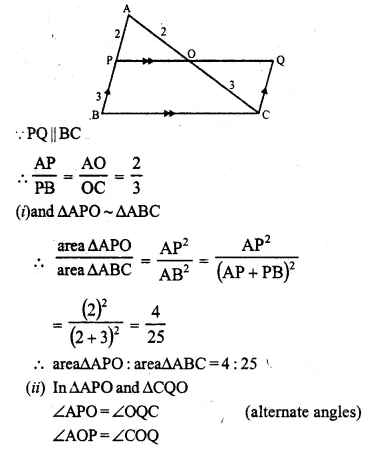
In ∆ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA.

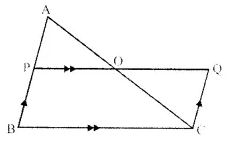
Find: (i) area ∆APO : area ∆ABC.
(ii) area ∆APO : area ∆CQO.
Solution:
In ∆ABC,
AP : PB = 2 : 3
PQ || BC and CQ || BA

Question 29.
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.

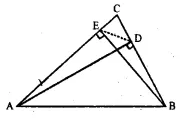
Show that:
(i) ∆ADC ~ ∆BEG
(ii) CA x CE = CB x CD
(iii) ∆ABC ~ ∆DEC
(iv) CD x AB = CA x DE
Solution:
In ∆ABC, AD ⊥ BC and BE ⊥ AC, DE is joined
To prove:
(i) ∆ADC ~ ∆BEG
(ii) CA x CE = CB x CD
(iii) ∆ABC ~ ∆DEC
(iv) CD x AB = CA x DE
Proof:
(i) In ∆ADC and ∆BEC,
∠C = ∠C (common)
∠ABE = ∠BEC (each 90°)
∆ADC ~ ∆BEC (AA axiom)

Question 30.
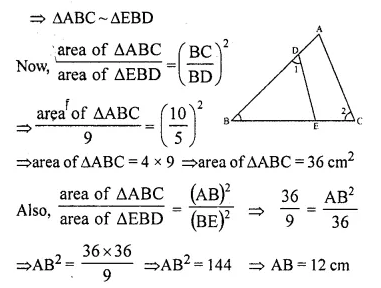
In the given figure, ABC is a triangle-with ∠EDB = ∠ACB. Prove that ∆ABC ~ ∆EBD.
If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ∆BED = 9 cm². Calculate the
(i) length of AB
(ii) area of ∆ABC

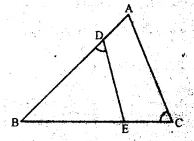
Solution:
In ∆ABC and ∆EBD
∠1 = ∠2 (given)
∠B = ∠B (common)

Question 31.
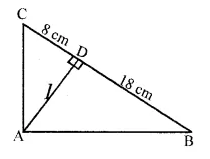
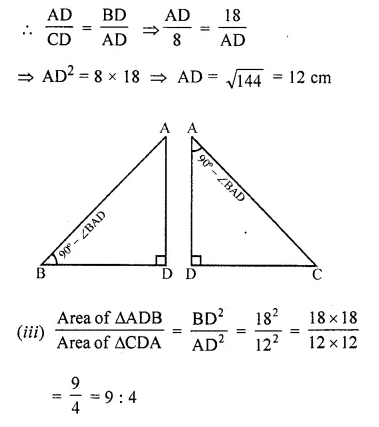
In the given figure, ABC is a right-angled triangle with ∠BAC = 90°.
(i) Prove ∆ADB ~ ∆CDA.
(ii) If BD = 18 cm, CD = 8 cm, find AD.
(iii) Find the ratio of the area of ∆ADB is to area of ∆CDA.

Solution:
(i) In ∆ADB and ∆CDA :
∠ADB = ∠ADC [each = 90°]
∠ABD = ∠CAD [each = 90° – ∠BAD]
∆ADB ~ ∆CDA [by AA similarity axiom]
(ii) Since, ∆ADB ~ ∆CDA

Question 32.
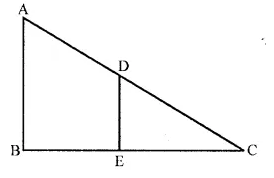
In the given figure, AB and DE are perpendicular to BC.
(i) Prove that ∆ABC ~ ∆DEC
(ii) If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
(iii) Find the ratio of the area of ∆ABC : area of ∆DEC.

Solution:
(i) To prove : ∆ABC ~ ∆DEC
In ∆ABC and ∆DEC
∠ABC = ∠DEC = 90°
∠C = ∠C (common)
∆ABC ~ ∆DEC (by AA axiom)

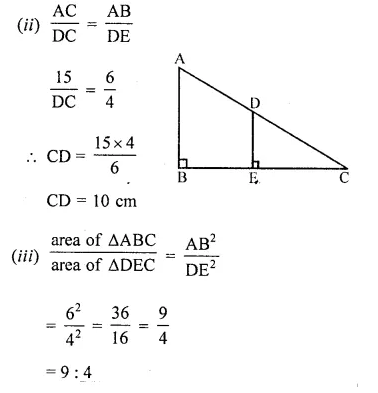
Question 33.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that:

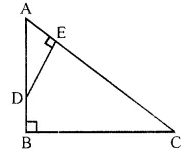
(i) ∆ADE ~ ∆ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of ∆ADE : area of quadrilateral BCED. (2015)
Solution:
In the given figure,
∆ABC is right angled triangle right angle at B.
D is any point on AB and DE ⊥ AC
To prove:
(i) ∆ADE ~ ∆ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm.Find DE and AD.
(iii) Find, area of ∆ADE : area of quadrilateral BCED
Proof:
(i) In ∆ADE and ∆ACB
∠A = ∠A (common)
∠E = ∠B (each = 90°)
∆ADE ~ ∆ACB. (AAaxiom)
(ii) AC = 13 cm, BC = 5 cm, AE = 4 cm
∆ADE ~ ∆ACB.

Question 34.

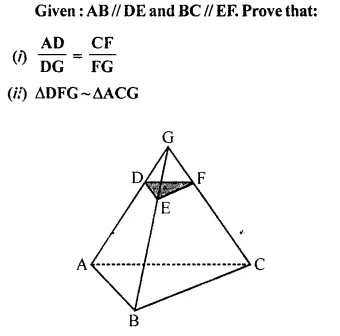
Solution:
In the given figure, AB || DE, BC || EF

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.