ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test
Solve the following equations (1 to 24) by factorization
Question 1.
(i) 4x² = 3x
(ii) \(\frac { { x }^{ 2 }-5x }{ 2 } =0\)
Solution:
(i) 4x² = 3x
x(4x – 3) = 0
Either x = 0,
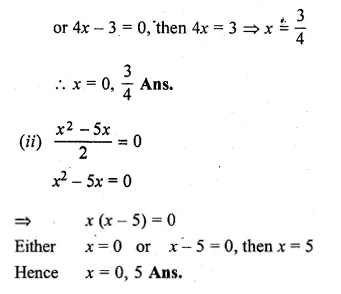
Question 2.
(i) (x – 3) (2x + 5) = 0
(ii) x (2x + 1) = 6
Solution:
(i) (x – 3) (2x + 5) = 0
Either x – 3 = 0,
Then x = 3
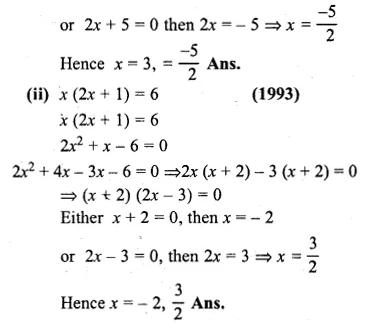
Question 3.
(i) x² – 3x – 10 = 0
(ii) x(2x + 5) = 3
Solution:
(i) x² – 3x – 10 = 0
⇒ x² – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0
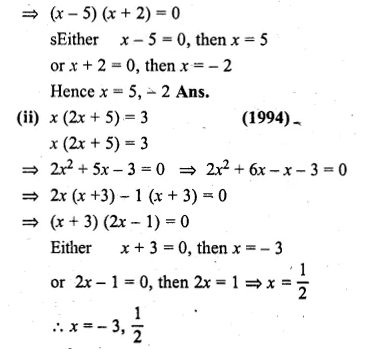
Question 4.
(i) 3x² – 5x – 12 = 0
(ii) 21x² – 8x – 4 = 0
Solution:
(i) 3x² – 5x – 12 = 0
⇒ 3x² – 9x + 4x – 12 = 0
⇒ 3x (x – 3) + 4(x – 3) = 0
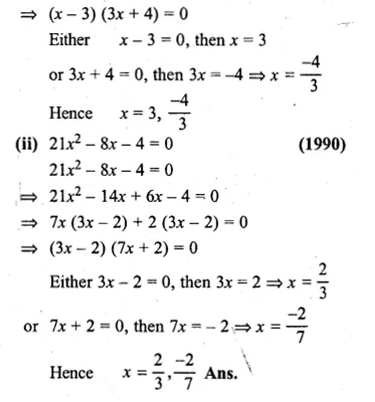
Question 5.
(i) 3x² = x + 4
(ii) x(6x – 1) = 35
Solution:
(i) 3x² = x + 4
⇒ 3x² – x – 4 = 0
⇒ 3x² – 4x + 3x – 4 = 0
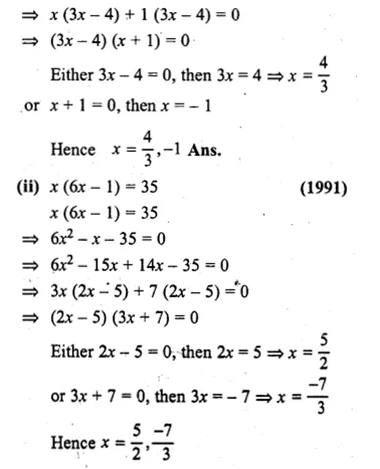
Question 6.
(i) 6p² + 11p – 10 = 0
(ii) \(\frac { 2 }{ 3 } { x }^{ 2 }-\frac { 1 }{ 3 } x=1 \)
Solution:
(i) 6p² + 11p – 10 = 0
⇒ 6p² + 15p – 4p – 10 = 0
⇒ 3p(2p + 5) – 2(2p + 5) = 0
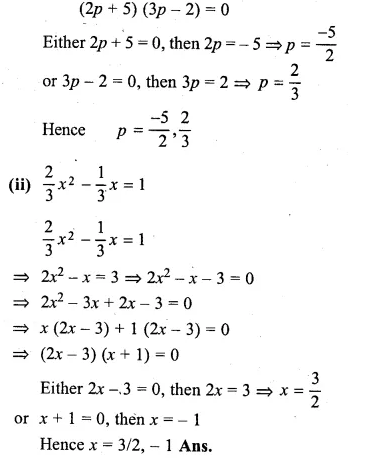
Question 7.
(i) (x – 4)² + 5² = 13²
(ii) 3(x – 2)² = 147
Solution:
(i) (x – 4)² + 5² = 13²
x² – 8x + 16 + 25 = 169
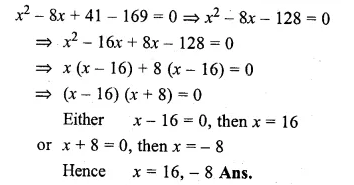
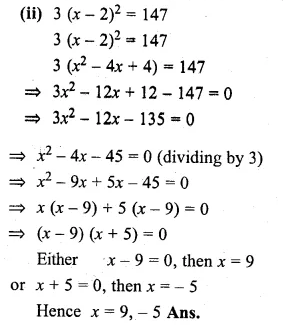
Question 8.
(i) \(\\ \frac { 1 }{ 7 } \)(3x – 5)² = 28
(ii) 3(y² – 6) = y(y + 7) – 3
Solution:
(i) \(\\ \frac { 1 }{ 7 } \)(3x – 5)² = 28
(3x – 5)² = 28 × 7
⇒ 9x² – 30x + 25 = 196
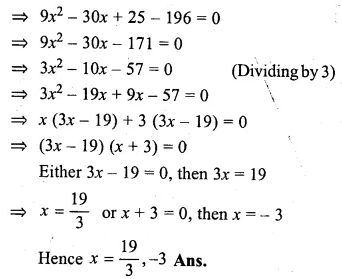
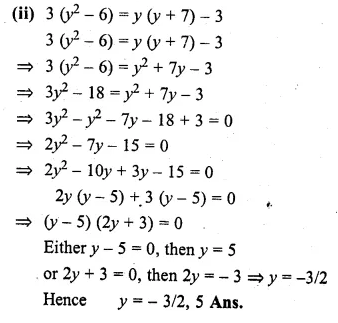
Question 9.
x² – 4x – 12 = 0,when x∈N
Solution:
x² – 4x – 12 = 0
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6) = 0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then x = 6
or x + 2 = 0, then x = -2
But -2 is not a natural number
∴ x = 6
Question 10.
2x² – 8x – 24 = 0 when x∈I
Solution:
2x² – 8x – 24 = 0
⇒ x² – 4x – 12 = 0 (Dividing by 2)
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6) = 0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then, x = 6
or x + 2 = 0, then x = – 2
Hence x = 6, – 2
Question 11.
5x² – 8x – 4 = 0 when x∈Q
Solution:
5x² – 8x – 4 = 0
∵ 5 × ( – 4) = – 20
-20 = – 10 + 2
-8 = – 10 + 2
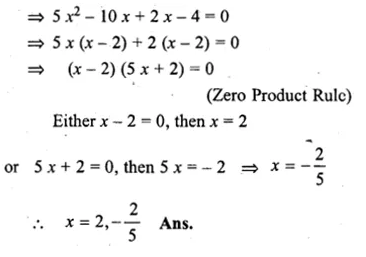
Question 12.
2x² – 9x + 10 = 0,when
(i)x∈N
(ii)x∈Q
Solution:
2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x(x – 2) – 5(x – 2) = 0
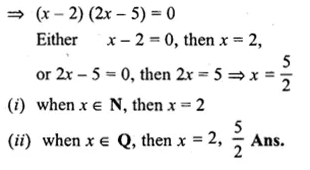
Question 13.
(i) a²x² + 2ax + 1 = 0, a≠0
(ii) x² – (p + q)x + pq = 0
Solution:
(i) a²x² + 2ax + 1 = 0
⇒ a²x² + ax + ax + 1 = 0
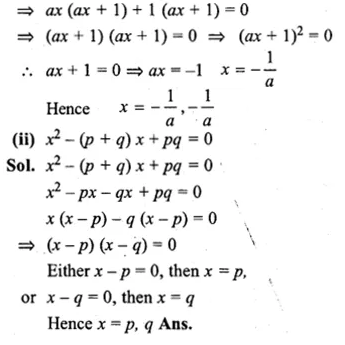
Question 14.
a²x² + (a² + b²)x + b² = 0, a≠0
Solution:
a²x² + (a² + b²)x + b² = 0
⇒ a²x(x + 1) + b²(x + 1) = 0
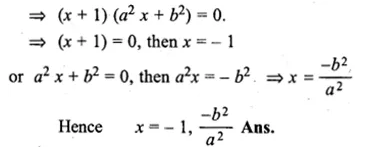
Question 15.
(i) √3x² + 10x + 7√3 = 0
(ii) 4√3x² + 5x – 2√3 = 0
Solution:
(i) √3x² + 10x + 7√3 = 0
[ ∵ √3 x 7√3 = 7 x 3 = 21]
⇒ √3x(x + √3) + 7(x + √3) = 0
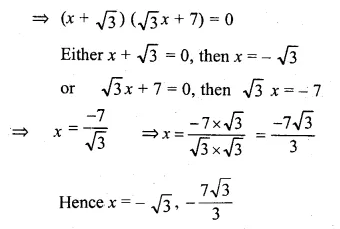
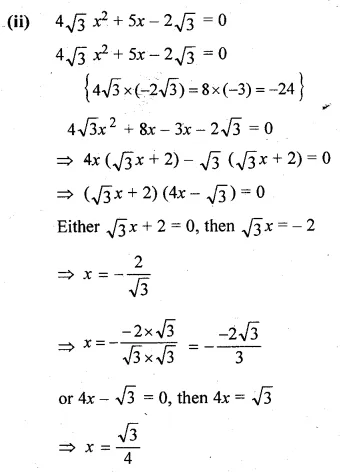
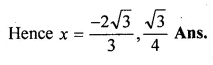
Question 16.
(i) x² – (1 + √2)x + √2 = 0
(ii) \(x+ \frac { 1 }{ x } \) = \(2 \frac { 1 }{ 20 } \)
Solution:
(i) x² – (1 + √2)x + √2 = 0
⇒ x² – x – √2x + √2 = 0
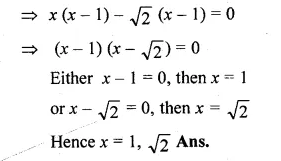
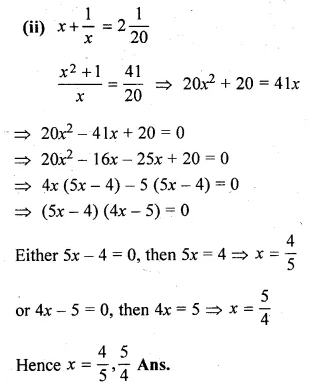
Question 17.
(i) \(\frac { 2 }{ { x }^{ 2 } } -\frac { 5 }{ x } +2=0,x\neq 0 \)
(ii)\(\frac { { x }^{ 2 } }{ 15 } -\frac { x }{ 3 } -10=0 \)
Solution:
(i) \(\frac { 2 }{ { x }^{ 2 } } -\frac { 5 }{ x } +2=0,x\neq 0 \)
⇒ 2 – 5x + 2x² = 0
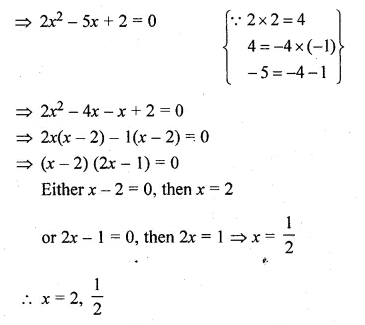
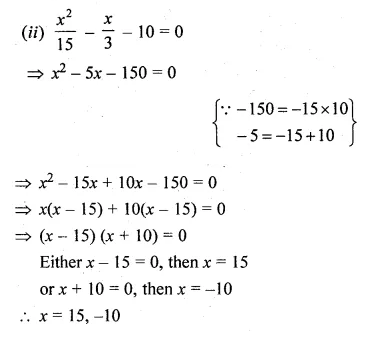
Question 18.
(i) \(3x-\frac { 8 }{ x } =2 \)
(ii) \(\frac { x+2 }{ x+3 } =\frac { 2x-3 }{ 3x-7 } \)
Solution:
(i) \(3x-\frac { 8 }{ x } =2 \)
\(\frac { { 3x }^{ 2 }-8 }{ x } =2 \)
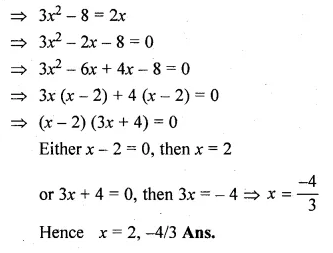
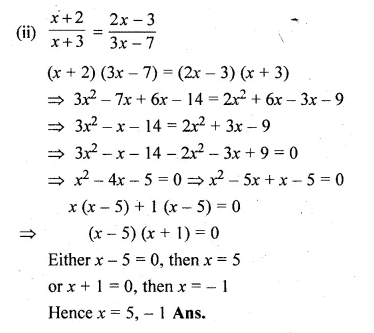
Question 19.
(i) \(\frac { 8 }{ x+3 } -\frac { 3 }{ 2-x } =2 \)
(ii) \(\frac { x }{ x-1 } +\frac { x-1 }{ x } =2\frac { 1 }{ 2 } \)
Solution:
(i) \(\frac { 8 }{ x+3 } -\frac { 3 }{ 2-x } =2 \)
\(\frac { 16-8x-3x-9 }{ (x+3)(2-x) } =2 \)
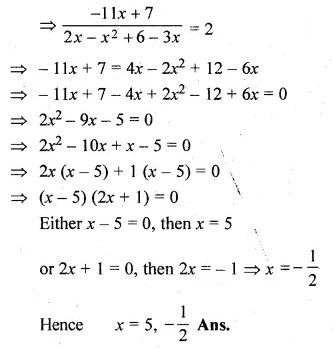
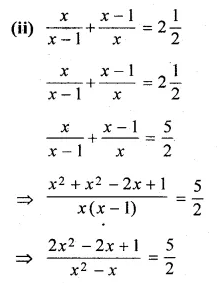
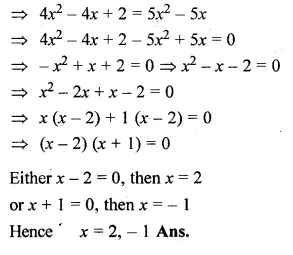
Question 20.
(i) \(\frac { x }{ x+1 } +\frac { x+1 }{ x } =\frac { 34 }{ 15 } \)
(ii) \(\frac { x+1 }{ x-1 } +\frac { x-2 }{ x+2 } =3 \)
Solution:
(i) \(\frac { x }{ x+1 } +\frac { x+1 }{ x } =\frac { 34 }{ 15 } \)
\(\frac { { x }^{ 2 }+{ x }^{ 2 }+2x+1 }{ x(x+1) } =\frac { 34 }{ 15 } \)
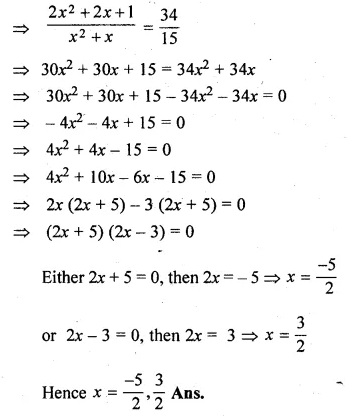
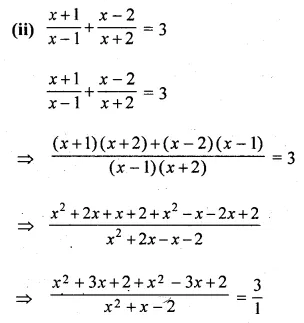
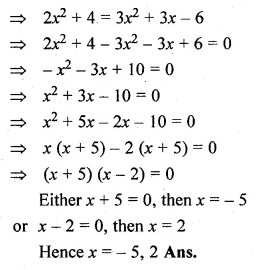
Question 21.
(i) \(\frac { 1 }{ x-3 } -\frac { 1 }{ x+5 } =\frac { 1 }{ 6 } \)
(ii) \(\frac { x-3 }{ x+3 } +\frac { x+3 }{ x-3 } =2\frac { 1 }{ 2 } \)
Solution:
(i) \(\frac { 1 }{ x-3 } -\frac { 1 }{ x+5 } =\frac { 1 }{ 6 } \)
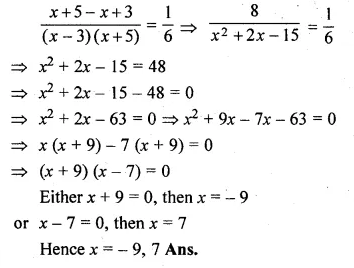
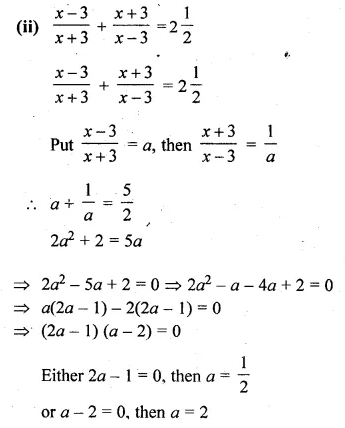
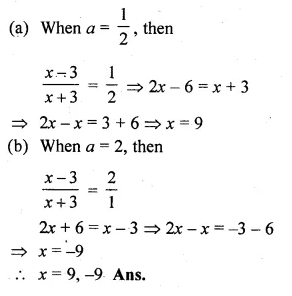
Question 22.
(i) \(\frac { a }{ ax-1 } +\frac { b }{ bx-1 } =a+b,a+b\neq 0,ab\neq 0\)
(ii) \(\frac { 1 }{ 2a+b+2x } =\frac { 1 }{ 2a } +\frac { 1 }{ b } +\frac { 1 }{ 2x } \)
Solution:
(i) \(\frac { a }{ ax-1 } +\frac { b }{ bx-1 } =a+b\)
⇒ \(\left( \frac { a }{ ax-1 } -b \right) +\left( \frac { b }{ bx-1 } -a \right) =0\)
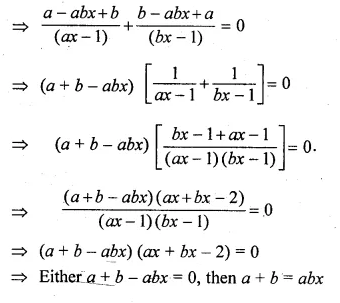
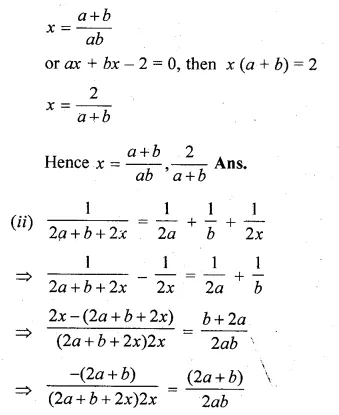
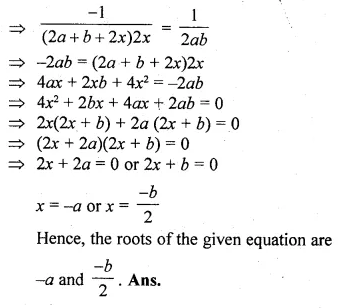
Question 23.
\(\frac { 1 }{ x+6 } +\frac { 1 }{ x-10 } =\frac { 3 }{ x-4 } \)
Solution:
\(\frac { 1 }{ x+6 } +\frac { 1 }{ x-10 } =\frac { 3 }{ x-4 } \)
⇒ \(\frac { x-10+x+6 }{ (x+6)(x-10) } =\frac { 3 }{ x-4 } \)
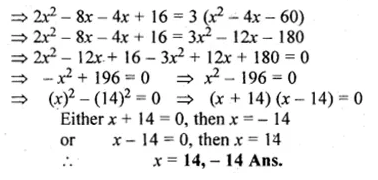
Question 24.
(i) \(\sqrt { 3x+4 } =x\)
(ii) \(\sqrt { x(x-7) } =3\sqrt { 2 } \)
Solution:
(i) \(\sqrt { 3x+4 } =x\)
Squaring on both sides
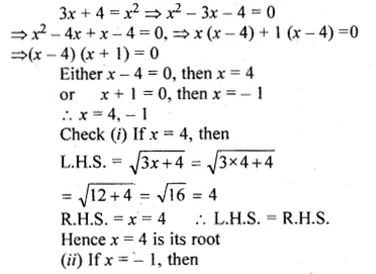

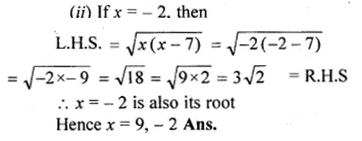
Question 25.
Use the substitution y = 3x + 1 to solve for x : 5(3x + 1 )² + 6(3x + 1) – 8 = 0
Solution:
y = 3x + 1
Now, 5(3x + 1)² + 6(3x + 1) – 8 = 0
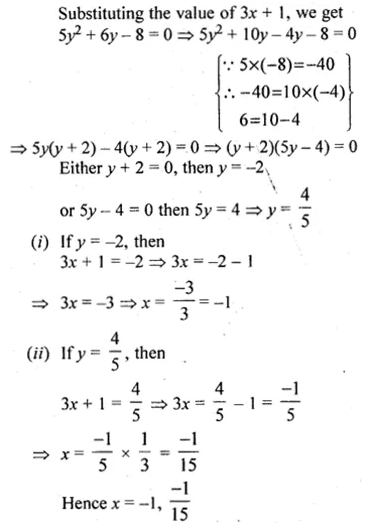
Question 26.
Find the values of x if p + 1 =0 and x² + px – 6 = 0
Solution:
p + 1 = 0, then p = – 1
Substituting the value of p in the given quadratic equation
x² + ( – 1)x – 6 = 0
⇒ x² – x – 6 = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x (x – 3) + 2 (x – 3) = 0
⇒ (x – 3) (x + 2) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = – 2
Hence x = 3, -2
Question 27.
Find the values of x if p + 7 = 0, q – 12 = 0 and x² + px + q = 0,
Solution:
p + 7 = 0, then p = – 7
and q – 12 = 0, then q = 12
Substituting the values of p and q in the given quadratic equation,
x² – 7x + 12 = 0
⇒ x² – 3x – 4x + 12 = 0
⇒ x (x – 3) – 4 (x – 3) = 0
⇒ (x – 3) (x – 4) = 0
Either x – 3 = 0, then x = 3
or x – 4 = 0, then x = 4
Hence x = 3, 4
Question 28.
If x = p is a solution of the equation x(2x + 5) = 3, then find the value of p.
Solution:
Given, x = p and x(2x + 5) = 3
Substituting the value of p, we get
p(2p + 5) = 3
⇒ 2p² + 5p – 3 = 0
⇒ 2p² + 6p – p – 3 = 0
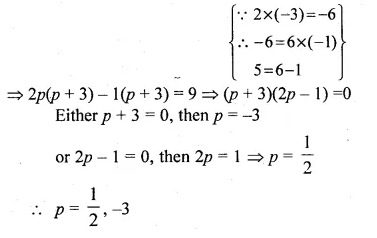
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.