RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5

RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Question 1.
Show that the following numbers are irrational
(i) \(\frac { 1 }{ \surd 2 }\)
(ii) 7 √5
(iii) 6 + √2
(iv) 3 – √5
Solution:



But it contradics that because √5 is irrational
3 – √5 is irrational

Question 2.
Prove that following numbers are irrationals :
(i) \(\frac { 2 }{ \surd 7 }\)
(ii) \(\frac { 3 }{ 2\surd 5 }\)
(iii) 4 + √2
(iv) 5 √2
Solution:




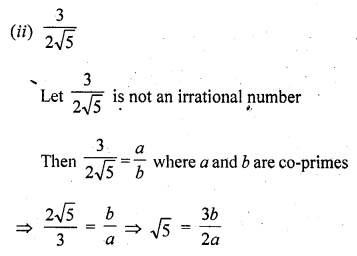
5 √2 is an irrational number

Question 3.
Show that 2 – √3 is an irrational number. [C.B.S.E. 2008]
Solution:
Let 2 – √3 is not an irrational number

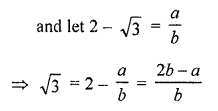
√3 is a rational number
But it contradicts because √3 is an irrational number
2 – √3 is an irrational number
Hence proved.

Question 4.
Show that 3 + √2 is an irrational number.
Solution:
Let 3 + √2 is a rational number

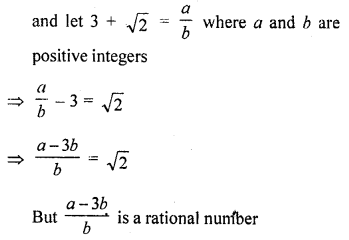
and √2 is irrational
But our suppositon is wrong
3 + √2 is an irrational number

Question 5.
Prove that 4 – 5√2 is an irrational number. [CBSE 2010]
Solution:
Let 4 – 5 √2 is not are irrational number
and let 4 – 5 √2 is a rational number
and 4 – 5 √2 = \(\frac { a }{ b }\) where a and b are positive prime integers

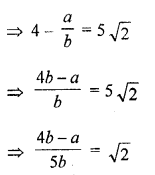
√2 is a rational number
But √2 is an irrational number
Our supposition is wrong
4 – 5 √2 is an irrational number

Question 6.
Show that 5 – 2 √3 is an irrational number.
Solution:
Let 5 – 2 √3 is a rational number
Let 5 – 2 √3 = \(\frac { a }{ b }\) where a and b are positive integers

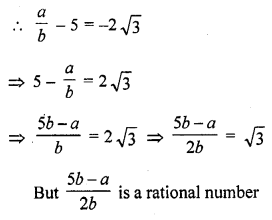
and √3 is a rational number
Our supposition is wrong
5 – 2 √3 is a rational number

Question 7.
Prove that 2 √3 – 1 is an irrational number. [CBSE 2010]
Solution:
Let 2 √3 – 1 is not an irrational number
and let 2 √3 – 1 a ration number
and then 2 √3 – 1 = \(\frac { a }{ b }\) where a, b positive prime integers

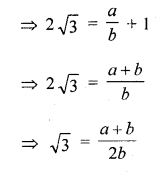
√3 is a rational number
But √3 is an irrational number
Our supposition is wrong
2 √3 – 1 is an irrational number

Question 8.
Prove that 2 – 3 √5 is an irrational number. [CBSE 2010]
Solution:
Let 2 – 3 √5 is not an irrational number and let 2 – 3 √5 is a rational number
Let 2 – 3 √5 = \(\frac { a }{ b }\) where a and b are positive prime integers

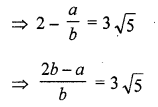
\(\Longrightarrow \frac { 2b-a }{ 3b } =\surd 5\)
√5 is a rational
But √5 is an irrational number
Our supposition is wrong
2 – 3 √5 is an irrational

Question 9.
Prove that √5 + √3 is irrational.
Solution:
Let √5 + √3 is a rational number
and let √5 + √3 = \(\frac { a }{ b }\) where a and b are co-primes

√3 is a rational number
But it contradics as √3 is irrational number
√5 + √3 is irrational

Question 10.
Prove that √2 + √3 is an irrational number.
Solution:
Let us suppose that √2 + √3 is rational.
Let √2 + √3 = a, where a is rational.
Therefore, √2 = a – √3
Squaring on both sides, we get

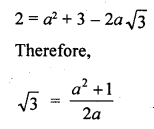
which is a contradiction as the right hand side is a rational number while √3 is irrational.
Hence, √2 + √3 is irrational.

Question 11.
Prove that for any prime positive integer p, √p is an irrational number.
Solution:
Suppose √p is not a rational number
Let √p be a rational number
and let √p = \(\frac { a }{ b }\)
Where a and b are co-prime number


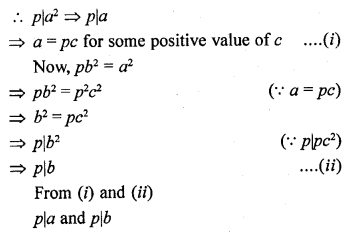
But it contradicts that a and b are co-primes
Hence our supposition is wrong
√p is an irrational

Question 12.
If p, q are prime positive integers, prove that √p + √q is an irrational number
Solution:


Hence proved.

Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.