RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Question 1.
The exponent of 2 in the prime factorisation of 144, is
(a) 4
(b) 5
(c) 6
(d) 3
Solution:
(a)

Question 2.
The LCM of two numbersls 1200. Which of the following cannot be their HCF ?
(a) 600
(b) 500
(c) 400
(d) 200
Solution:
(b) LCM of two number = 1200
Their HCF of these two numbers will be the factor of 1200
500 cannot be its HCF

Question 3.
If n = 2³ x 3⁴ x 4⁴ x 7, then the number of consecutive zeroes in n, where n is a natural number, is
(a) 2
(b) 3
(c) 4
(d) 7
Solution:
(c) Because it has four factors n = 2³ x 3⁴ x 4⁴ x 7
It has 4 zeroes

Question 4.
The sum of the exponents of the prime factors in the prime factorisation of 196, is
(a) 1
(b) 2
(c) 4
(d) 6
Solution:
(c)

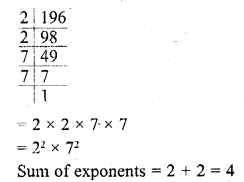
Question 5.
The number of decimal places after which the decimal expansion of the rational number \(\frac { 23 }{ { 2 }^{ 2 }\times 5 }\) will terminate, is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b)

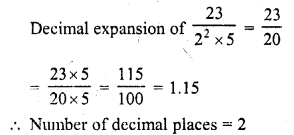
Question 6.

(a) an even number
(b) an odd number
(c) an odd prime number
(d) a prime number
Solution:
(a)

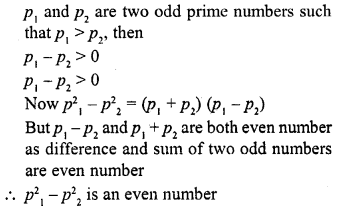
Question 7.
If two positive integers a and b are expressible in the form a = pq² and b = p²q ; p, q being prime numbers, then LCM (a, b) is
(a) pq
(b) p³q³
(c) p³q²
(d) p²q²
Solution:
(c) a and b are two positive integers and a =pq² and b = p³q, where p and q are prime numbers, then LCM=p³q²

Question 8.
In Q. No. 7, HCF (a, b) is
(a) pq
(b) p³q³
(c) p³q²
(d) p²q²
Solution:
(a) a = pq² and b =p³q where a and b are positive integers and p, q are prime numbers, then HCF =pq

Question 9.
If two positive integers tn and n arc expressible in the form m = pq³ and n = p³q², where p, q are prime numbers, then HCF (m, n) =
(a) pq
(b) pq²
(c) p³q³
(d) p²q³
Solution:
(b) m and n are two positive integers and m = pq³ and n = pq², where p and q are prime numbers, then HCF = pq²

Question 10.
If the LCM of a and 18 is 36 and the HCF of a and 18 is 2, then a =
(a) 2
(b) 3
(c) 4
(d) 1
Solution:
(c) LCM of a and 18 = 36
and HCF of a and 18 = 2
Product of LCM and HCF = product of numbers
36 x 2 = a x 18
a = \(\frac { 36\times 2 }{ 18 }\) = 4

Question 11.
The HCF of 95 and 152, is
(a) 57
(b) 1
(c) 19
(d) 38
Solution:
(c) HCF of 95 and 152 = 19

Question 12.
If HCF (26, 169) = 13, then LCM (26, 169) =
(a) 26
(b) 52
(f) 338
(d) 13
Solution:
(c) HCF (26, 169) = 13
LCM (26, 169) = \(\frac { 26\times 169 }{ 13 }\) = 338

Question 13.

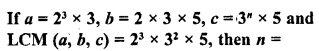
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b)

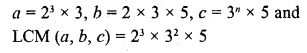
Question 14.
The decimal expansion of the rational \(\frac { 14587 }{ 1250 }\) number will terminate after
(a) one decimal place
(b) two decimal place
(c) three decimal place
(d) four decimal place
Solution:
(d)

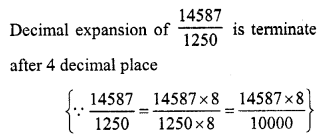
Question 15.
If p and q are co-prime numbers, then p² and q² are
(a) co prime
(b) not co prime
(c) even
(d) odd
Solution:
(a) p and q are co-prime, then
p² and q² will also be coprime

Question 16.
Which of the following rational numbers have terminating decimal ?

(a) (i) and (ii)
(b) (ii) and (iii)
(c) (i) and (iii)
(d) (i) and (iv)
Solution:
(d) We know that a rational number has terminating decimal if the prime factors of its denominator are in the form 2^m x 5ⁿ
\(\frac { 16 }{ 225 }\) and \(\frac { 7 }{ 250 }\) has terminating decimals

Question 17.
If 3 is the least prime factor of number a and 7 is the least prime factor of number b, then the least prime factor of a + b, is
(a) 2
(b) 3
(c) 5
(d) 10
Solution:
(a) 3 is the least prime factor of a
7 is the least prime factor of b, then
Sum of a a and b will be divisible by 2
2 is the least prime factor of a + b

Question 18.
\(3.\bar { 27 }\) is
(a) an integer
(b) a rational number
(c) a natural number
(d) an irrational number
Solution:
(b) \(3.\bar { 27 }\) is a rational number

Question 19.
The smallest number by which √27 should be multiplied so as to get a rational number is
(a) √27
(b) 3√3
(c) √3
(d) 3
Solution:
(c)

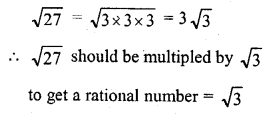
Question 20.
The smallest rational number by which \(\frac { 1 }{ 3 }\) should be multiplied so that its decimal expansion terminates after one place of decimal, is
(a) \(\frac { 3 }{ 10 }\)
(b) \(\frac { 1 }{ 10 }\)
(c) 3
(d) \(\frac { 3 }{ 100 }\)
Solution:
(a) The smallest rational number which should be multiplied by \(\frac { 1 }{ 3 }\) to get a terminating

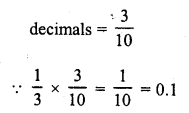
Question 21.
If n is a natural number, then 9²ⁿ – 4²ⁿ is always divisible by
(a) 5
(b) 13
(c) both 5 and 13
(d) None of these
Solution:
(c)

Question 22.
If n is any natural number, then 6ⁿ – 5ⁿ always ends with
(a) 1
(b) 3
(c) 5
(d) 7
Solution:
(a) n is any natural number and 6ⁿ – 5ⁿ
We know that 6ⁿ ends with 6 and 5ⁿ ends with 5
6ⁿ – 5ⁿ will end with 6 – 5 = 1

Question 23.
The LCM and HCF of two rational numbers are equal, then the numbers must be
(a) prime
(b) co-prime
(c) composite
(d) equal
Solution:
(d) LCM and HCF of two rational numbers are equal Then those must be equal

Question 24.
If the sum of LCM and HCF of two numbers is 1260 and their LCM is 900 more than their HCF, then the product of two numbers is
(a) 203400
(b) 194400
(c) 198400
(d) 205400
Solution:
(b) Sum of LCM and HCF of two numbers = 1260
LCM = 900 more than HCF
LCM = 900 +HCF
But LCM = HCF = 1260
900 + HCF + HCF = 1260
=> 2HCF = 1260 – 900 = 360
=> HCF = 180
and LCM = 1260 – 180 = 1080
Product = LCM x HCF = 1080 x 180 = 194400
Product of numbers = 194400

Question 25.
The remainder when the square of any prime number greater than 3 is divided by 6, is
(a) 1
(b) 3
(c) 2
(d) 4
Solution:
(a)

Question 26.
For some integer m, every even integer is of the form
(a) m
(b) m + 1
(c) 2m
(d) 2m + 1
Solution:
(c) We know that, even integers are 2, 4, 6, …
So, it can be written in the form of 2m Where, m = Integer = Z
[Since, integer is represented by Z]
or m = …, -1, 0, 1, 2, 3, …
2m = …, -2, 0, 2, 4, 6, …
Alternate Method
Let ‘a’ be a positive integer.
On dividing ‘a’ by 2, let m be the quotient and r be the remainder.
Then, by Euclid’s division algorithm, we have
a – 2m + r, where a ≤ r < 2 i.e., r = 0 and r = 1
=> a = 2 m or a = 2m + 1
When, a = 2m for some integer m, then clearly a is even.

Question 27.
For some integer q, every odd integer is of the form
(a) q
(b) q + 1
(c) 2q
(d) 2q + 1
Solution:
(d) We know that, odd integers are 1, 3, 5,…
So, it can be written in the form of 2q + 1 Where, q = integer = Z
or q = …, -1, 0, 1, 2, 3, …
2q + 1 = …, -3, -1, 1, 3, 5, …
Alternate Method
Let ‘a’ be given positive integer.
On dividing ‘a’ by 2, let q be the quotient and r be the remainder.
Then, by Euclid’s division algorithm, we have
a = 2q + r, where 0 ≤ r < 2
=> a = 2q + r, where r = 0 or r = 1
=> a = 2q or 2q + 1
When a = 2q + 1 for some integer q, then clearly a is odd.

Question 28.
n² – 1 is divisible by 8, if n is
(a) an integer
(b) a natural number
(c) an odd integer
(d) an even integer
Solution:
(c)


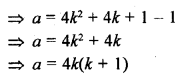
At k = -1, a = 4(-1)(-1 + 1) = 0 which is divisible by 8.
At k = 0, a = 4(0)(0 + 1) = 4 which is divisible by 8.
At k = 1, a = 4(1)(1 + 1) = 8 which is divisible by 8.
Hence, we can conclude from above two cases, if n is odd, then n² – 1 is divisible by 8.

Question 29.
The decimal expansion of the rational number \(\frac { 33 }{ { 2 }^{ 2 }\times 5 }\) will terminate after
(a) one decimal place
(b) two decimal places .
(c) three decimal places
(d) more than 3 decimal places
Solution:
(b)

Question 30.
If two positive integers a and b are written as a = x³y² and b = xy³ ; x, y are prime numbers, then HCF (a, b) is
(a) xy
(b) xy²
(c) x³y³
(d) x²y²
Solution:
(b)

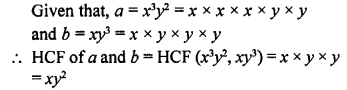
[Since, HCF is the product of the smallest power of each common prime factor involved in the numbers]

Question 31.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(a) 10
(b) 100
(c) 504
(d) 2520
Solution:
(d) Factors of 1 to 10 numbers
1 = 1
2 = 1 x 2
3 = 1 x 3
4 = 1 x 2 x 2
5 = 1 x 5
6 = 1 x 2 x 3
7 = 1 x 7
8 = 1 x 2 x 2 x 2
9 = 1 x 3 x 3
10 = 1 x 2 x 5
LCM of number 1 to 10 = LCM (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
= 1 x 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Question 32.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is
(a) 13
(b) 65
(c) 875
(d) 1750
Solution:
(a) Since, 5 and 8 are the remainders of 70 and 125, respectively. Thus, after subtracting these remainders from the numbers, we have the numbers 65 = (70 – 5), 117 = (125 – 8), which is divisible by the required number.
Now, required number = HCF of 65, 117
[For the largest number]
For this, 117 = 65 x 1 + 52 [Dividend = divisor x quotient + remainder]
=> 65 = 52 x 1 + 13
=> 52 = 13 x 4 + 0
HCF = 13
Hence, 13 is the largest number which divides 70 and 125, leaving remainders 5 and 8.

Question 33.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is
(a) 4
(b) 2
(c) 1
(d) 3
Solution:
(b) By Euclid’s division algorithm,
b = aq + r, 0 ≤ r < a [dividend = divisor x quotient + remainder]
=> 117 = 65 x 1 + 52
=> 65 = 52 x 1 + 13
=> 52 = 13 x 4 + 0
HCF (65, 117)= 13 …(i)
Also, given that HCF (65, 117) = 65m – 117 …..(ii)
From equations (i) and (ii),
65m – 117 = 13
=> 65m = 130
=> m = 2

Question 34.
The decimal expansion of the rational number \(\frac { 14587 }{ 1250 }\) will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Solution:
(d)

Hence, given rational number will terminate after four decimal places.

Question 35.
Euclid’s division lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy
(a) 1 < r < b
(b) 0 < r ≤ b
(c) 0 ≤ r < b
(d) 0 < r < b
Solution:
(c) According to Euclid’s Division lemma, for a positive pair of integers there exists unique integers q and r, such that
a = bq + r, where 0 ≤ r < b

Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQSare helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

You can also download MCQ Questions For Class 10 Maths With Answers to help you to revise complete syllabus and score more marks in your examinations.