NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2.
- Practical Geometry Class 6 Ex 14.1
- Practical Geometry Class 6 Ex 14.3
- Practical Geometry Class 6 Ex 14.4
- Practical Geometry Class 6 Ex 14.5
- Practical Geometry Class 6 Ex 14.6
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 6 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | Practical Geometry |
| Exercise | Ex 14.2 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2
Question 1.
Draw a line segment of length 7.3 cm. using a ruler.
Solution :
Using ruler, we mark two points A and B which are 7.3 cm apart. Join A and B and get AB. \(\overline { AB }\) is a line segment of length 7.3 cm.
![]()
Question 2.
Construct a line segment of length 5.6 cm using ruler and compasses.
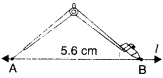
Solution :
Step 1. Draw a line l. Mak a point A on line l.
Step 2. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto the 5.6 cm mark.
Step 3. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at B.
Step 4. AB is a line segment of required length.
Question 3.
Construct \(\overline { AB }\) of length 7.8 cm. From this cut off \(\overline { AC }\) of length 4.7 cm. Measure \(\overline { BC }\).
Solution :
Steps of Construction
Step 1. Draw a line l. Mark a point A on line l.
Step 2. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto the 7.8 cm mark.
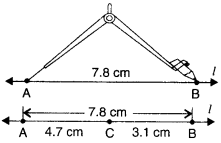
Step 3. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at B.
Step 4. \(\overline { AB }\) is a line segment of length 7.8 cm.
Step 5. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto 4.7 cm mark.
Step 6. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at C.
Step 7. \(\overline { AC }\) is a line segment of length 4.7 cm. On measurement. \(\overline { BC }\) =3.1 cm.
Question 4.
Given \(\overline { AB }\) of length 3.9 cm, construct \(\overline { PQ }\) such that the length of \(\overline { PQ }\) is twice that of AB Verify by measurement.
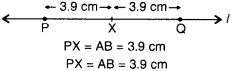
(Hint : Construct \(\overline { PX }\) such that length of PX = length of \(\overline { AB }\); then cut off \(\overline { XQ }\) such that \(\overline { XQ }\) also has the length of \(\overline { AB }\)).
Solution :
Steps of Construction
Step 1. Draw a line I. Mark a point P on line l.
Step 2. Place the compasses pointer on the A mark of the given line segment \(\overline { AB }\) . Open it to place the pencil point upto B mark of the given line segment \(\overline { AB }\).
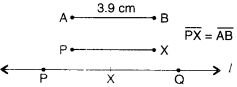
Step 3. Without changing the opening of the compasses, place the pointer on P and swing an arc to cut l at X.
Step 4. Again without changing the opening of the compasses place the compasses pointer on the X mark of line / and swing an arc to cut / at Q.
Step 5. \(\overline { PQ }\) is a line segment of length twice that of \(\overline { AB }\). Please verify yourself by measurement.
Question 5.
Given \(\overline { AB }\) of length 7.3 cm and \(\overline { CD }\) of length 3.4 cm, construct a line segment \(\overline { XY }\) such that the length of \(\overline { XY }\) is equal to the difference between the lengths of \(\overline { AB }\) and \(\overline { CD }\) . Verify by measurement.
Solution :
Steps of Construction
Step 1. Draw a line l. Mark a point X on line l.
Step 2. Place the compasses pointer on the A mark of the given line segment \(\overline { AB }\). Open it to place the pencil point upto B mark of the given line segment \(\overline { AB }\).
Step 3. Without changing the opening of the compasses, place the pointer of compasses on X and swing an arc to cut / at ∠.
Step 4. Place the compasses pointer on the C mark of the given line segment \(\overline { CD }\). Open it to place the pencil point upto D mark of the given line segment \(\overline { CD }\).
Step 5. Without changing the opening of the compasses, place the pointer of compasses on ∠ and swing an arc towards X to cut l at Y.
Step 6. \(\overline { XY }\) is a required line segment of length = the difference between the lengths of \(\overline { AB }\) and \(\overline { CD }\).
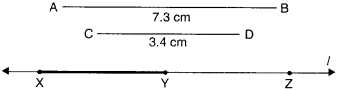
Please verify yourself by measurement.
We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2, drop a comment below and we will get back to you at the earliest.