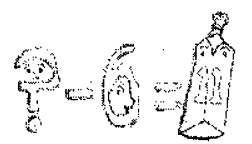Tag: NCERT Solutions for Class 6 Maths

NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9.

• Understanding Elementary Shapes Class 6 Ex 5.1
• Understanding Elementary Shapes Class 6 Ex 5.2
• Understanding Elementary Shapes Class 6 Ex 5.3
• Understanding Elementary Shapes Class 6 Ex 5.4
• Understanding Elementary Shapes Class 6 Ex 5.5
• Understanding Elementary Shapes Class 6 Ex 5.6
• Understanding Elementary Shapes Class 6 Ex 5.7
• Understanding Elementary Shapes Class 6 Ex 5.8

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 5
Chapter Name	Understanding Elementary Shapes
Exercise	Ex 5.9
Number of Questions Solved	2
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9

Chapter 5 Understanding Elementary Shapes Ex 5.9

Question 1.
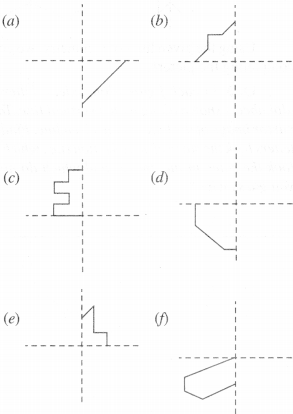
Match the following :
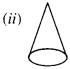
(a) Cone

(b) Sphere

(c) Cylinder

(d) Cuboid

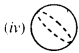
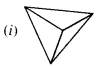
(e) Pyramid

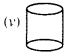
Give two new examples of each shape.
Solution :
(a) ↔ (ii)
(b) ↔ (iv)
(c) ↔ (v)
(d) ↔ (iii)
(e) ↔ (i).
(i) Birthday cap, ice-cream cone
(ii) Tennis Ball, laddu
(iii) Road-roller, gas cylinder
(iv) Brick, book
(v) Pyramids of Egypt, right pyramid.

Question 2.
What shape is
(a) Your installments box?
(b) A brick?
(c) A matchbox?
(d) A road-roller?
(e) A sweet laddu?
Solution :
(a) Cuboid
(b) Cuboid
(c) Cuboid
(d) Cylinder
(e) Sphere.

We hope the NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6.

• Practical Geometry Class 6 Ex 14.1
• Practical Geometry Class 6 Ex 14.2
• Practical Geometry Class 6 Ex 14.3
• Practical Geometry Class 6 Ex 14.4
• Practical Geometry Class 6 Ex 14.5

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 14
Chapter Name	Practical Geometry
Exercise	Ex 14.6
Number of Questions Solved	9
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6

Question 1.
Draw ∠POQ of measure 75° and find its line of symmetry.
Solution :

Step 1. Draw a ray \(\overline { OQ }\).
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark point P at 75°
Step 4. Join \(\overline { OP }\). Then, ∠POQ = 75°.
Step 5. With O as center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q’.
Step 6. With Q’ as center, draw (in the interior of ∠POQ) an arc whose radius is more than half the length Q’F.
Step 7. With the same radius and with F as center, draw another arc in the interior of ∠POQ. Let
the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ which is also the line of symmetry of ∠POQ as ∠POR = ∠ROQ.

Question 2.
Draw an angle of measure 147° and construct its bisector.
Solution :

Step 1. Draw \(\overline { OQ }\) of any length.
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark a point P at 147°.
Step 4. Join OP. Then, ∠POQ = 147°.
Step 5. With O as center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q’.
Step 6. With Q’ as center, draw (in the interior of ∠POQ) an arc whose radius is more than half the length Q’F.
Step 7. With the same radius and with F as center, draw another arc in the interior of ∠POQ. Let the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ.

Question 3.
Draw a right angle and construct its bisector.
Solution :
Step 1. Draw a ray OQ.
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark point P at 90°.
Step 4. Join \(\overline { OP }\). Then, ∠POQ = 90°.
Step 5. With O as center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q’.
Step 6. With Q’ as center, draw (in the interior of ∠POQ) an arc whose radius is more than half th length Q’F.
Step 7. With the same radius and with P center, draw another arc in the interior of ∠POQ the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ.

Question 4.
Draw an angle of measure 153° and divide it into four equal parts.
Solution :
Step 1. Draw a ray \(\overline { OQ }\).
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark a point P at 153°.
Step 4. Join OP. Then, ∠POQ = 153°.
Step 5. With O as the center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q.
Step 6. With Q’ as the center, draw (in the interior of ∠POQ) an arc whose radius is more than half the length Q’F.
Step 7. With the same radius and with F as a center, draw another arc in the interior of ∠POQ. Let the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ.

Step 8. With O as a center and using compasses, draw an arc that cuts both rays of ∠ROQ. Label the points of intersection as B and A.
Step 9. With A as a center, draw (in the interior of ∠ROQ) an arc whose radius is more than half the length AB.
Step 10. With the same radius and with B as a center, draw another arc in the interior of ∠ROQ. Let the two arcs intersect at S. Then, \(\overline { OS }\) is the bisector of ∠ROQ.
Step 11. With O as a center and using compasses, draw an arc that cuts both rays of ∠POR. Label the points of intersection as D and C.
Step 12. With C as a center, draw (in the interior of ∠POR) an arc whose radius is more than half the length CD.
Step 13. With the same radius and with D as centre, draw another arc in the interior of ∠POR. Let the two arcs intersect at T. Then, \(\overline { OT }\) is the bisector of ∠POR. Thus, \(\overline { OS }\), \(\overline { OR }\) and \(\overline { OT }\) divide ∠POQ = 153° into four equal parts.

Question 5.
Construct with ruler and compasses, angles of following measures:
(a) 60°
(b) 30°
(c) 90°
(d) 120°
(e) 45°
(f) 135°.
Solution :
(a) Construction of an angle of measure 60°

Step 1. Draw a line PQ and mark a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line PQ at a point say A.
Step 3. With the pointer at A (as center), now draw an arc that passes through O.
Step 4. Let the two arcs intersect at B. Join OB. We get ∠BOA whose measure is 60°.

(b) Construction of an angle of measure 30°

Step 1. Draw a line PQ and mark a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line PQ at a point say A.
Step 3. With the pointer at A (as center), now draw an arc that passes through O.
Step 4. Let the two arcs intersect at B. Join OB. We get ∠BOA whose measure is 60°.
Step 5. With O as a center and using compasses, draw an arc that cuts both rays of ∠BOA. Label the points of intersection as D and C.
Step 6. With C as a center, draw (in the interior of ∠BOA) an arc whose radius is more than half the length CD.
Step 7. With the same radius and with D as a center, draw another arc in the interior of ∠BOA. Let the two arcs intersect at E. Then, \(\overline { OE }\) is the bisector of ∠BOA, i.e., ∠BOE = ∠EOA = 30°.

(c) Construction of an angle of measure 90°

Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc where the radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COL. Let
the two arcs intersect at F. Join \(\overline { OF }\). Then, \(\overline { OF }\) is the bisector of ∠COB, i.e., ∠COF = ∠FOB. Now, ∠ FOQ = 90°.

(d) Construction of an angle of measure 120°

Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compass es at O and draw an arc of convenient radius which puts the line at A. • ‘
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the i alius > on the compasses and with B as a center, draw an arc which cuts the first arc at C. .
Step 5. Join OC. Then, ∠COA is the required angle whose measure is 120°.

(e) Construction of an angle of measure 45°

Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COB. Let the two arcs intersect at F. Join OF. Then, ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays to ∠FOQ. Label the points of the intersection as G and H.
Step 10. With H as a center, draw (in the interior of. ∠FOQ) an arc whose radius is more than half the length HG.
Step 11. With the same radius and with G as a center, draw another arc in the interior of ∠FOQ. Let the two arcs intersect at I. Join OI. Then, OI is the bisector of ∠FOH, i.e., ∠FOI = ∠IOH. Now,
∠FOI = ∠IOH = 45°.

(f) Construction of an angle of measure 135° it.

Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as the center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as the center, draw another arc in the interior of ∠COB. Let the two arcs intersect at F. Join \(\overline { OF }\). Then, \(\overline { OF }\) is the bisector of ∠COB, i.e., ∠COF = ∠FOB. Now, ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays of ∠POF. Label the points of intersection as G and H.
Step 10. With H as center draw (in the interior of ∠POF) an arc whose radius is more than half the length HG.
Step 11. With the same radius and with G as a center, draw another arc in the interior of ∠POF. Let
the two arcs intersect at I. Join 01. Then, \(\overline { OI }\) is the bisector of ∠POF, i.e., ∠GOI = ∠IOF. Now, ∠IOQ = 135°.

Question 6.
Draw an angle of measure 45° and bisect it.
Solution :

Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A. ’
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COB. Let
the two arcs intersect at F. Join OF. Then ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays of ∠FOQ. Label the points of intersection on G and H.
Step 10. With G as a center, draw in the interior of ∠FOQ) an arc whose radius is more than half the length HG.
Step 11. With the same radius and with G as a center, draw another arc in the interior of ∠FOQ. Let the two arcs intersect at I. Join OI. Then OI is the bisector of ∠FOQ, i.e., ∠FOI = ∠IOH. Now, ∠FOI = ∠IOH = 45°.
Step 12. With O as a center and using compasses, draw an arc that cuts both rays of ∠IOH. Label the points of intersection as J and K.
Step 13. With K as a center, draw (in the interior of ∠IOH) an arc whose radius is more than half the length KJ.
Step 14. With the same radius and with J as a center, draw another arc in the interior of ∠IOH. Let the two arcs intersect at L. Join OL. Then OL is the bisector of ∠IOH, i.e., ∠IOL = ∠LOK \(22\frac { 1^{ \circ } }{ 2 }\) .

Question 7.
Draw an angle of measure 135° and bisect it.
Solution :

Step 1. Draw any line PQ and take a point O on.
Step 2. Place the pointer of the compasses at’ and draw an arc of convenient radius which cul line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COB. Let
the two arcs intersect at F. Join \(\overline { OF }\). Then \(\overline { OF }\) is the bisector of ∠COB, i.e., ∠COF = ∠FOB. Now, ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays of ∠POF. Label the points of intersection as G and H.
Step 10. With G as a center, draw in the interior of ∠POF an arc whose radius is more than half the length HG.
Step 11. With the same radius and with H as a centre, draw another arc in the interior of ∠POF. Let
the two arcs intersect at I. Join \(\overline { OI }\). Then \(\overline { OI }\) is the bisector of ∠POF, i.e., ∠POI = ∠IOF. Now, ∠IOQ = 135°. .
Step 12. With O as centre and using compasses, draw an arc that cuts both rays of ∠IOQ. Label the points of intersection as J and K.
Step 13. With K as centre, draw (in the interior of ∠IOQ) an arc whose radius is more than half the length KJ.
Step 14. With the same radius and with J as centre, draw another arc in the interior of ∠IOQ. Let the two arcs intersect at L. Join \(\overline { OL }\). Then \(\overline { OL }\) is the bisector of ∠IOQ, i.e., ∠IOL = ∠LOQ.

Question 8.
Draw an angle of 70°. Make a copy of it using only a straight edge and compasses.
Solution :
Steps of construction
1. Construct an angle ABC = 70°.
2. Take a line z and mark a point D on it.
3. Fix the compasses pointer on B and draw an arc which cuts the sides of ∠ABC at D and E.
4. Without changing the compasses setting, place the pointer on P and draw an arc which cuts ∠ at Q.
5. Open the compasses equal to length DE.


6. Without disturbing the radius on compasses, place its pointer at Q and draw an arc which cuts the previous arc at R.
7. Join PR and draw ray PR. It gives ∠RPQ which is the required angle whose measure is equal to the measure of ∠ABC.

Question 9.
Draw an angle of 40°. Copy its supplementary angle.
Solution :
Steps of construction


1. Draw ∠CAB = 40°.
2. Draw a line I and mark a point P on it.
3. Place the pointer of the compasses on A and draw an arc which cuts extended BA at E and AC at F.
4. Without changing the radius on compasses, place its pointer at P and draw an arc which cuts l at Q.
5. Open the length of compasses equal to EF.
6. Without disturbing the radius on compasses, place its pointer at Q and draw an arc which cuts the previous arc at R.
7. Join QR and draw ray QR. It gives ∠RQS which is the required angle whose measure

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5.

• Practical Geometry Class 6 Ex 14.1
• Practical Geometry Class 6 Ex 14.2
• Practical Geometry Class 6 Ex 14.3
• Practical Geometry Class 6 Ex 14.4
• Practical Geometry Class 6 Ex 14.6

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 14
Chapter Name	Practical Geometry
Exercise	Ex 14.5
Number of Questions Solved	9
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5

Question 1.
Draw \(\overline { AB }\) of length 7.3 cm and find its axis of symmetry.
Solution :
Step 1. Draw a line segment \(\overline { AB }\) of length 7.3 cm.
Step 2. With A ascentere, using compasses, drawthe circle. The radius of this circle should be more than half of the length of \(\overline { AB }\).

Step 3. With the same radius and with B as a centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 4. Join CD. Then, \(\overline { CD }\) is the axis of symmetry of \(\overline { AB }\).

Question 2.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solution :
Step 1. Draw a line segment \(\overline { AB }\) of length 9.5 cm.

Step 2. With A as a centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { AB }\).
Step 3. With the same radius and with B as a centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 4. Join CD. Then \(\overline { CD }\) is the perpendicular bisector of the line segment \(\overline { AB }\).

Question 3.
Draw the perpendicular bisector of \(\overline { XY }\) whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the midpoint of \(\overline { XY }\), what can you say about the lengths MX and XY ?
Solution :
Step 1. Draw a line segment \(\overline { XY }\) of length 10.3 cm.
Step 2. With X as a centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { XY }\).

Step 3. With the same radius and with Y as a centre, draw another circle using compasses. Let it cuts the previous circle at A and B.
Step 4. Join AB. Then \(\overline { AB }\) is the perpendicular bisector of the line segment \(\overline { XY }\).
(a) On examination, we find that PX = PY.
(b) We can say that the lengths of MX is half of the length of XY.

Question 4.
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.

Solution :
Step 1. Draw a line segment \(\overline { AB }\) of length 12.8 cm.
Step 2. With A as centre, using compasses, draw two arcs on either side of AB. The radius of this arc should be more than fialf of the length of \(\overline { AB }\).
Step 3. With the same radius and with B as centre, draw another arcs using compasses. Let it cut the previous arcs at C and D.
Step 4. Join \(\overline { CD }\). It cuts \(\overline { AB }\) at E. Then \(\overline { CD }\) is the perpendicular bisector of the line segment \(\overline { AB }\).
Step 5. With A as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of AE.
Step 6. With the same radius and with E as centre, draw another circle using compasses; Let it cut the previous circle at F and G.
Step 7. Join \(\overline { FG }\). It cuts \(\overline { AE }\) at H. Then \(\overline { FG }\) is the perpendicular bisector of the line segment \(\overline { AE }\).
Step 8. With E as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of EB.
Step 9. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at I and J.
Step 10. Join \(\overline { IJ }\). It cuts \(\overline { EB }\) at K. Then \(\overline { IJ }\) is the perpendicular bisector of the line segment \(\overline { EB }\). Now, the points H, E and K divide AB into four equal parts, i.e., \(\overline { AH }\) = \(\overline { HE }\) = \(\overline { EK }\) = \(\overline { KB }\) By measurement, \(\overline { AH }\) = \(\overline { HE }\) = \(\overline { EK }\) = \(\overline { KB }\) = 3.2 cm.

Question 5.
With \(\overline { PQ }\) of length 6.1 cm as diameter draw a circle.
Solution :
Step 1. Draw a line segment \(\overline { PQ }\) of length 6.1 cm.

Step 2. With P as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { PQ }\).
Step 3. With the same radius and with Q as centre, draw another circle using compasses. Let it cut the previous circle at A and B.
Step 4. Join \(\overline { AB }\). It cuts \(\overline { PQ }\) at C. Then \(\overline { AB }\) is
the perpendicular bisector of the line segment PQ .
Step 5. Place the pointer of the compasses at C and open the pencil upto P.
Step 6. Turn the compasses slowly to draw the circle.

Question 6.
Draw a circle with centre C and radius, 3.4 cm. Draw any chord \(\overline { AB }\). Construct the perpendicular bisector of \(\overline { AB }\) and examine if it passes through C.
Solution :

Step 1. Draw a point with a sharp pencil and mark it as C.
Step 2. Open the compasses for the required radius 3.4 cm, by putting the pointer on 0 and opening the pencil upto 3.4 cm.
Step 3. Place the pointer of the compasses at C. Step 4. Turn the compasses slowly to draw the
circle.
Step 5. Draw any chord \(\overline { AB }\) of this circle.
Step 6. With A as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { AB }\).
Step 7. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at D and E.
Step 8. Join \(\overline { DE }\) . Then \(\overline { DE }\) is the perpendicular bisector of the line segment \(\overline { AB }\). On examination, we find that it passes through C.

Question 7.
Repeat Question 6, if \(\overline { AB }\) happens to be a diameter.
Solution :
Step 1. Draw a point with a sharp pencil and mark it as C.
Step 2. Open the compasses for the required radius 3.4 cm, by putting the pdinter of compasses on 0 of the scale and opening the pencil upto 3.4 cm.
Step 3. Place the pointer of the compasses at C.
Step 4. Turn the compasses slowly to draw the circle.
Step 5. Draw any diameter \(\overline { AB }\).

Step 6. With A as centre, using compasses, draw arcs on either side. The radius of this arc should be more than half of the length of \(\overline { AB }\).
Step 7. With the same radius and with B as centre, draw another arcs using compasses. Let it cut the previous arcs at D and E.
Step 8. Join \(\overline { DE }\) . Then \(\overline { DE }\) is the perpendicular bisector of the line segment \(\overline { AB }\). On examination, we find that it passes through C.

Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution :

Step 1. Draw a point with a sharp pencil and mark it as O.
Step 2. Open the compasses for the required radius of 4 cm. by putting the pointer on 0 and opening the pencil upto 4 cm.
Step 3. Place the pointer of the compasses at O.
Step 4. Turn the compasses slowly to draw the circle.
Step 5. Draw any two chords \(\overline { AB }\) and \(\overline { CD }\) of this circle.
Step 6. With A as centre, using compasses, draw two arcs on either side of AB. The radius of this arc should be more than half of the length of \(\overline { AB }\).
Step 7. With the same radius and with B as centre, draw another two arcs using compasses. Let it cut the previous circle at E and F.
Step 8. Join \(\overline { EF }\). Then \(\overline { EF }\) is the perpendicular bisector of the chord \(\overline { AB }\).
Step 9. With C a< centre, using compasses, draw two arcs on either side of CD. The radius of this arc should be more than half of the length of \(\overline { CD }\).
Step 10. With the same radius and with D as centre, draw another two arcs using compasses. Let it cut the previous circle at G and H.
Step 11. Join \(\overline { GH }\). Then \(\overline { GH }\) is the perpendi¬cular bisector of the chord \(\overline { CD }\). We find that the perpendicular bisectors \(\overline { EF }\) and \(\overline { GH }\) meet at O, the centre of the circle.

Question 9.
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA- OB. Draw the perpendicular bisectors of \(\overline { OA }\) and \(\overline { OB }\). Let them meet at P. Is PA = PB?
Solution :
Step 1. Draw any angle POQ with vertex O.
Step 2. Take a point A on the arm OQ and another point B on the arm OP such that \(\overline { OA }\) = \(\overline { OB }\).
Step 3. With O as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { OA }\).

Step 4. With the same radius and with A as centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 5. Join \(\overline { CD }\). Then \(\overline { CD }\) is the perpendicular bisector of the line segment \(\overline { OA }\).
Step 6. With O as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { OB }\).
Step 7. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at E and F.
Step 8. Join \(\overline { EF }\). Then \(\overline { EF }\) is the perpendicular bisector of the line segment OB. The two perpendicu¬lar bisectors meet at P.
Step 9. Join \(\overline { PA }\) and \(\overline { PB }\). We find that \(\overline { PA }\) = \(\overline { PB }\).

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4.

• Practical Geometry Class 6 Ex 14.1
• Practical Geometry Class 6 Ex 14.2
• Practical Geometry Class 6 Ex 14.3
• Practical Geometry Class 6 Ex 14.5
• Practical Geometry Class 6 Ex 14.6

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 14
Chapter Name	Practical Geometry
Exercise	Ex 14.4
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4

Question 1.
Draw any line segment \(\overline { AB }\) . Mark any point M on it. Through M draw a perpendicular to \(\overline { AB }\). (use ruler and compasses).
Solution :
Step 1. Given a point M on any line \(\overline { AB }\).

Step 2. With M as centre and a convenient radius, construct a part circle (arc) intersecting the line segment \(\overline { AB }\) at two points C and D.
Step 3. With C and D as centres and a radius greater than CM, construct two arcs which cut each other at N.
Step 4. Join \(\overline { MN }\). Then \(\overline { MN }\) is perpendicular to \(\overline { AB }\) at M, i.e., \(\overline { MN }\) \(\overline { AB }\).

Question 2.
Draw any’line segment \(\overline { PQ }\). Take any point R not on it. Through R draw a perpendicular to \(\overline { PQ }\). (use ruler and set-square).
Solution :
Step 1. Let \(\overline { PQ }\) be the given line segment and R be a point not on it.

Step 2. Place a set-square on \(\overline { PQ }\) such that one arm of the right angle aligns along \(\overline { PQ }\).
Step 3. Place a ruler along the edge opposite of the right angle.
Step 4. Hold the ruler fixed. Slide the set-square along the ruler all the point R touches the arm of the set-square.
Step 5. Join RS along the edge through R, meeting \(\overline { PQ }\) at S. Now \(\overline { RS }\) \(\overline { PQ }\).

Question 3.
Draw a line l and a point X on it. Through X, draw a line segment \(\overline { XY }\) perpendicular to l. Now draw a perpendicular to XY at Y. (use ruler and compasses)
Solution :
Step 1. Given a point X on a line l.
Step 2. With X as centre and a convenient radius, construct a part circle (arc) intersecting the line l at two points A and B.
Step 3. With A and B as centres and a radius greater than AX, construct two arcs which cut each other at Y.

Step 4. Join \(\overline { XY }\). Then \(\overline { XY }\) is perpendicular to l atX, i.e., \(\overline { XY }\) l.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3.

• Practical Geometry Class 6 Ex 14.1
• Practical Geometry Class 6 Ex 14.2
• Practical Geometry Class 6 Ex 14.4
• Practical Geometry Class 6 Ex 14.5
• Practical Geometry Class 6 Ex 14.6

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 14
Chapter Name	Practical Geometry
Exercise	Ex 14.3
Number of Questions Solved	2
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3

Question 1.
Draw any line segment \(\overline { PQ }\). Without measuring \(\overline { PQ }\) . construct a copy of \(\overline { PQ }\).
Solution :
Step 1. Given \(\overline { PQ }\) whose length is not known.
Step 2. Fix the compasses pointer on P and the pencil end on Q. The opening of the instrument now
gives the length of \(\overline { PQ }\).
Step 3. Draw any line l. Choose a point A on /. Without changing the compasses setting, place the pointer on A.
Step 4. Swing an arc that cuts l at a point, say, B. Now \(\overline { AB }\) is a copy of \(\overline { PQ }\).

Question 2.
Given some line segment \(\overline { AB }\), whose length you do not know, construct \(\overline { PQ }\) such that the length of \(\overline { PQ }\) is twice that of \(\overline { AB }\).
Solution :
Step 1. Given \(\overline { AB }\) whose length is not known.
Step 2. Fix the compasses pointer on A and the pencil end on B. The opening of the instrument now gives the length of \(\overline { AB }\).
Step 3. Draw any line l. Choose a point P on l. Without changing the compasses setting, place the pointer on P.
Step 4. Strike an arc that cuts l at a point, say, X.
Step 5. Now fix the compasses pointer on X. Strike an arc away from P that cuts l at a point, say, Q. Now, the length of \(\overline { PQ }\) is twice that of \(\overline { AB }\).

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2.

• Practical Geometry Class 6 Ex 14.1
• Practical Geometry Class 6 Ex 14.3
• Practical Geometry Class 6 Ex 14.4
• Practical Geometry Class 6 Ex 14.5
• Practical Geometry Class 6 Ex 14.6

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 14
Chapter Name	Practical Geometry
Exercise	Ex 14.2
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2

Question 1.
Draw a line segment of length 7.3 cm. using a ruler.
Solution :
Using ruler, we mark two points A and B which are 7.3 cm apart. Join A and B and get AB. \(\overline { AB }\) is a line segment of length 7.3 cm.

Question 2.
Construct a line segment of length 5.6 cm using ruler and compasses.

Solution :
Step 1. Draw a line l. Mak a point A on line l.
Step 2. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto the 5.6 cm mark.
Step 3. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at B.
Step 4. AB is a line segment of required length.

Question 3.
Construct \(\overline { AB }\) of length 7.8 cm. From this cut off \(\overline { AC }\) of length 4.7 cm. Measure \(\overline { BC }\).
Solution :
Steps of Construction
Step 1. Draw a line l. Mark a point A on line l.
Step 2. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto the 7.8 cm mark.

Step 3. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at B.
Step 4. \(\overline { AB }\) is a line segment of length 7.8 cm.
Step 5. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto 4.7 cm mark.
Step 6. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at C.
Step 7. \(\overline { AC }\) is a line segment of length 4.7 cm. On measurement. \(\overline { BC }\) =3.1 cm.

Question 4.
Given \(\overline { AB }\) of length 3.9 cm, construct \(\overline { PQ }\) such that the length of \(\overline { PQ }\) is twice that of AB Verify by measurement.

(Hint : Construct \(\overline { PX }\) such that length of PX = length of \(\overline { AB }\); then cut off \(\overline { XQ }\) such that \(\overline { XQ }\) also has the length of \(\overline { AB }\)).
Solution :
Steps of Construction
Step 1. Draw a line I. Mark a point P on line l.
Step 2. Place the compasses pointer on the A mark of the given line segment \(\overline { AB }\) . Open it to place the pencil point upto B mark of the given line segment \(\overline { AB }\).

Step 3. Without changing the opening of the compasses, place the pointer on P and swing an arc to cut l at X.
Step 4. Again without changing the opening of the compasses place the compasses pointer on the X mark of line / and swing an arc to cut / at Q.
Step 5. \(\overline { PQ }\) is a line segment of length twice that of \(\overline { AB }\). Please verify yourself by measurement.

Question 5.
Given \(\overline { AB }\) of length 7.3 cm and \(\overline { CD }\) of length 3.4 cm, construct a line segment \(\overline { XY }\) such that the length of \(\overline { XY }\) is equal to the difference between the lengths of \(\overline { AB }\) and \(\overline { CD }\) . Verify by measurement.
Solution :
Steps of Construction
Step 1. Draw a line l. Mark a point X on line l.
Step 2. Place the compasses pointer on the A mark of the given line segment \(\overline { AB }\). Open it to place the pencil point upto B mark of the given line segment \(\overline { AB }\).
Step 3. Without changing the opening of the compasses, place the pointer of compasses on X and swing an arc to cut / at ∠.
Step 4. Place the compasses pointer on the C mark of the given line segment \(\overline { CD }\). Open it to place the pencil point upto D mark of the given line segment \(\overline { CD }\).
Step 5. Without changing the opening of the compasses, place the pointer of compasses on ∠ and swing an arc towards X to cut l at Y.
Step 6. \(\overline { XY }\) is a required line segment of length = the difference between the lengths of \(\overline { AB }\) and \(\overline { CD }\).

Please verify yourself by measurement.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3.

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 13
Chapter Name	Symmetry
Exercise	Ex 13.3
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3

Question 1.
Find the number of lines of symmetry in each of the following shapes. How will you check your answers?


Solution :
(a)

Number of lines of symmetry = 4
(b)

Number of lines of symmetry = 1
(c)

Number of lines of symmetry = 2
(d)

Number of lines of symmetry = 2
(e)

Number of lines of symmetry = 1
(f)

Number of lines of symmetry = 2

Question 2.
Copy the following drawing on squared paper. Complete each one of them such that the resulting figure has the two dotted lines as two lines of symmetry :

How did you go about completing the picture?
Solution :




Using the given lines of symmetry, we go about completing the picture.

Question 3.
In each figure alongside, a letter of the alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e., which letters look the same in the image) and which do not. Can you guess why?

Solution :
The letter A looks the same after reflection but not the letter B. The reason is that in reflection, the sense of direction changes. In the given letters, the letters O, M, N, H, T, V, and X look the same after reflections because these letters have a vertical line of symmetry.

We hope the NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2.

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 13
Chapter Name	Symmetry
Exercise	Ex 13.2
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2

Question 1.
Find the number of lines of symmetry for each of the following shapes :

Solution :

Question 2.
Copy the triangle in each of the following figures, on squared paper. In each case, draw the line(s) of symmetry if any and identify the type of triangle. (Some of you may like to trace the figures and try paper-folding first!)

Solution :

Question 3.
Complete the following table :

Solution :

Question 4.
Can you draw a triangle which has
(a) exactly one line of symmetry?
(b) exactly two lines of symmetry?
(c) exactly three lines of symmetry?
(d) no lines of symmetry?
Sketch a rough figure in each case.
Solution :
(a) Yes; an isosceles triangle

(b) No
(c) Yes; an equilateral triangle

(d) Yes, an equilateral triangle

Question 5.
On a squared paper, sketch the following:
(a) A triangle with a horizontal line of symmetry’ but no vertical line of symmetry.
(b) A quadrilateral with both horizontal and vertical lines of symmetry.
(c) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.
(d) A hexagon with exactly two lines of symmetry.
(e) A hexagon with six lines of symmetry.
(Hint: It will be helpful if you first draw the lines of symmetry and then complete the figures.)
Solution :


Question 6.
Trace each figure and draw the lines of symmetry, if any :



Solution :

no line symmetry


Question 7.
Consider the letters of English alphabets A to Z. List among them the letters which have
(a) vertical lines of symmetry (like A)
(b) horizontal lines of symmetry (like B)
(c) no lines of symmetry (like Q)

Solution :
(a) A, H, I, M, O, T, U, V, W, X, Y
(b) B, C, D, E, H, I, K, O, X
(c) F, G, J, L, N, P, Q, R, S, Z

Question 8.
Given here are figures of a few folded sheets and designs drawn about the fold. In each case, draw a rough diagram of the complete figure that would be seen when the design is cut off.

Solution :

 

We hope the NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2.

• Ratio and Proportion Class 6 Ex 12.1
• Ratio and Proportion Class 6 Ex 12.3

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 12
Chapter Name	Ratio and Proportion
Exercise	Ex 12.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2

Question 1.
Determine if the following are in proportion:
(a) 15, 45, 40, 120
(b) 33, 121, 9, 96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
Solution :





Question 2.
Write True (T) or False (F) against each of the following statements :
(a) 16: 24: : 20: 30
(b) 21: 6: 35: 10
(c) 12: 18: 28: 12
(d) 8: 9: : 24: 27
(e) 5.2: 3.9: : 3: 4
(f) 0.9: 0.36: : 10: 4
Solution :




Question 3.
Are the following statements true₹ I
(a) 40 Persons : 200 Persons =₹ 15: ₹75 ;
(b) 7.5 litre : 15 litre = 5 kg : 10 kg 1
(c) 99 kg : 45 kg = f 44 : ₹20
(d) 32 m : 64 m = 6 sec: 12 sec
(e) 45 km: 60 km = 12 hours : 15 hours.
Solution :


Since the two ratios are equal, therefore, the given statement is true.

Since the two ratios are equal, therefore, the given statement is true.

Since, the two ratios are equal, therefore, the given statement is true.


Since the two ratios are equal, therefore the given statement is true.

Since the two ratios are not equal, therefore the given statement is false.

Question 4.
Determine if the following ratios form a proportion. Also, write the middle terms and extreme terms where the ratios form a proportion.
(a) 25 cm: 1 m and 7 40 : 7160
(b) 39 litre : 65 litre and 6 bottle : 10 bottle
(c) 2 kg : 80 kg and 25 g : 625 g
(d) 200 ml: 2.5 litre and ₹4 ; ₹ 50.
Solution :
(a)
∴ 1 m= 100 cm

Since the two ratios are equal, therefore, the given ratios are in proportion. Middle terms are 1 m and ₹ 40. Extreme terms are 25 cm and ₹ 160.

Since the two ratios are equal, therefore, the given ratios are in proportion. Middle terms are 65 liters and 6 bottles. Extreme terms are 39 liters and 10 bottles.


Since the two ratios are not equal, therefore, the given ratios are not in proportion.

Since the two ratios are equal, therefore, the given ratios are in proportion. Middle terms are 2.5 litres and ₹ 4. Extreme terms are 200 ml and ₹ 50.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5.

• Algebra Class 6 Ex 11.1
• Algebra Class 6 Ex 11.2
• Algebra Class 6 Ex 11.3
• Algebra Class 6 Ex 11.4

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 11
Chapter Name	Algebra
Exercise	Ex 11.5
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5

Question 1.
State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.
(a) 17 = x + 7
(b) (t-7)> 5
(c) \(\frac { 4 }{ 2 } \) =2
(d) (7 x 3)-19 = 8
(e) 5 x 4 – 8 =2x
(f) x – 2 =0
(g) 2m<30
(h) 2n+1=11
(i) 7=(11 x 5) -(12x 4)
(j) 7=(11×2)+p
(k) 20=5y
(l) latex]\frac { 3q }{ 2 } [/latex]<5
(m) z+12>24
(n) 20-(10-5)=3×5
(o) 7-x =5
Solution.

Question 2.
Complete the entries in the third column of the table.


Solution.
(a) Yes
(b) Yes
(c) No
(d) No
(e) No
(f) Yes
(g) No
(h) No
(i)  Yes
(j) Yes
(k) No
(l) No
(m) No
(n) No
(o) No
(p) No
(q) Yes

Question 3.
Pick out the solution from the values given bracket next to each equation. Show that the values do not satisfy the equation.
(a) 5m – 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p-5 = 5 (0, 10, 5,-5)
(d) \(\frac { q }{ 2 } \) = 7 (7, 2, 10, 14)
(e) r-4- 0 (4, – 4. 8, 0)
(f) x + 4 – . y (-2, 0, 2. 4)
Solution.
(a) Solution is 12
For m = 10
L.H.S. = 5 x 10 = 50 which is not equal to R.H.S.
For m = 5
L.H.S. = 5 x 5 = 25 which is not equal to R.H.S.
For m = 15
L.H.S. = 5 x 15 = 75 which is not equal to R.H.S.

(b) Solution is 8
For n = 12
L.H.S. = 12+12
= 24 which is not equal to R.H.S.
For n = 20
L.H.S. = 20+12
= 32 which is not equal to R.H.S.
For n =0
L.H.S. = 0+12
= 12 which is not equal to R.H.S.

(c) Solution is 10
For p = 0
L.H.S. = 0 – 5 = – 5 which is not equal to R.H.S.
For p = 5
L.H.S. = 5-5 = 0 which is not equal to R.H.S.
For p = – 5
L.H.S. = – 5 – 5 = – 10 which is not equal to R.H.S.

(d) Solution is 14
For g = 7
L.H.S. = \(\frac { q }{ 2 } \) which is not equal to R.H.S.
For q = 2
L.H.S. = \(\frac { 2 }{ 2 } \) = 1 which is not equal to R.H.S.
For q = 10
L.H.S. = \(\frac { 10 }{ 2 } \) = 5 which is not equal to R.H.S.

(e) Solution is 4
For r = – 4
L.H.S. = -4-4
= – 8 which is not equal to R.H.S.
For r = 8
L.H.S. = 8-4 = 4 which is not equal to R.H.S.
For r = 0
L.H.S. = 0 – 4 = – 4 which is not equal to R.H.S.

(f) Solution is – 2
For x = 0
L.H.S. = 0 + 4 = 4 which is not equal to R.H.S. For x = 2
L.H.S. = 2 + 4 = 6 which is not equal to R.H.S.
For x : = 4
L.H.S. = 4 + 4 = 8 which is not equal to R.H.S.

Question 4.
(a) Complete the table and by inspection of the table find the solution to the equation m + 10 = 16

(b) Complete the table and by inspection of the table find the solution to the equation 5t = 35

(c) Complete the table and find using the table the solution of the equation z/3 = 4

(d) Complete the table and find the solution to the equation m-7=3

Solution.

Question 5.
Solve the following riddles, you may yourself construct such riddles.
Who am I?
(i) Go round a square
Counting every corner
Thrice and no more!
Add the count to me
To get exactly thirty four!

(ii) For each day of the week
Make an account from me
If you make no mistake
You will get twenty three!

(iii) I am a special number
Take away from me a six!
A whole cricket team
You will still be able to fix!

(iv) Tell me who I am
I shall give a pretty clue!
You will get me back
If you take me out of twenty-two!
Solution.
(i) Let the required number be x.
Number of corners of the square = 4
Number obtained on counting every comer thrice = 4 x 3=12
According to the question, x + 12 = 34 ⇒ x = 34 -12 = 22
Hence, I am 22.

(ii) Let the required number be x.
Number of players in a cricket team = 11
According to the question.
x – 6 = 11  ⇒ x =11+6=17
Hence, lam 17.

(iii) Let the required number be v.
Number of days of a week = 7
According to the question.
x + 7 = 23    ⇒ x = 23-7 =16
Hence, lam 16.

(iv) Let the required number be x.
According to the question.
22 – x = x ⇒ x + x = 22
2x = 22    ⇒ x = \(\frac { 10 }{ 2 } \) = 11
Hence, lam 11.

We hope the NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5 help you. If you have any query regarding. NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4.

• Algebra Class 6 Ex 11.1
• Algebra Class 6 Ex 11.2
• Algebra Class 6 Ex 11.3
• Algebra Class 6 Ex 11.5

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 11
Chapter Name	Algebra
Exercise	Ex 11.4
Number of Questions Solved	2
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4

Question 1.
Answer the following :
(a) Take Sarita’s present age to he y years
(i) What will be her age 5 years from now?
(ii) What was her age 3 years back?
(iii) Sarita ‘s grandfather is 6 times her age. What is the age of her grandfather?
(iv) Grandmother is 2 years younger than grandfather. What is grandmother’s age?
(v) Sarita’sfather’s age is 5years more than 3 times Sarita’s age. What is her father’s age?
(b) The length of a rectangular hall is 4 meters less than 3 times the breadth of the hall. What is the length, if the breadth is b meters?
(c) A rectangular box has height h cm. Its length is 5 times the height and breadth is 10 cm less than the length. Express the length and the breadth of the box in terms of the height.
(d) Meena, Beena, and Leena are climbing the steps to the hilltop. Meena is at step s, Beena is 8 steps ahead and Leena7 steps behind. Where are Beena and Leena? The total number of steps to the hilltop is 10 less than 4 times what Meena has reached. Express the total number of steps using.
(e) A bus travels at v km per hour. It is going from Daspur to Beespur. After the bus has traveled 5 hours,
Beespur is still 20 km away. What is the distance from Daspur to Beespur? Express it using.

Solution.
(a) (y + 5) years
(ii) (y – 3) years
(iii) 6y years
(iv) (6y – 2) years
(v) (3y + 5) years
(b) Length (l) = (3b – 4) meters
(c) Length of the box = 5h cm
Breadth of the box = (5h – 10) cm
(d) Beena is at step (s + 8)
Leena is at step (s – 7)
Total number of steps = 4s – 10.
(e) Speed of the bus = v km/hr
Distance travelled in 5 hours = 5v km.
∴Total distance = (5v + 20) km

Question 2.
Change the following statements using expressions into statements in the ordinary language.
(For example, Given Salim scores r runs in a cricket match, Nalin scores (r+ 15) runs. In ordinary language—Nalin scores 15 runs more than Salim.)
(a) A notebook costs Rs p. A book costs Rs 3 p.
(b) Tony puts q marbles on the table. He has 8 q marbles in his box.
(c) Our class has n students. The school has 20n students.
(d) Jaggu is z years old. His uncle is 4z years old and his aunt is (4z- 3) years old.
(e) In an arrangement of dots, there are r rows. Each row contains 5 dots.
Solution.
(a) A book costs three times the cost of a notebook.
(b) Tony’s box contains 8 times the marbles on the table.
(c) The total number of students in the school in 20 times that of our class.
(d) Jaggu’s uncle is 4 times older than Jaggu and Jaggu’s aunt is 3 years younger than his uncle.
(e) The total number of dots in an arrangement is 5 times the number of rows.

Question 3.
(a) Given Munnu ’s age to be x years, can you guess what (x – 2) may show?
(Hint: Think of Munnu’s younger brother.) Can you guess what (x + 4) may show? What (3x + 7) may show?
(b) Given Sara’s age today to be y years. Think of her age in the future or in the past. What will the
following expression indicate? y + 7, y-3, y + 4\(\frac { 1 }{ 2 } \) ,y-2\(\frac { 1 }{ 2 } \).
(c) Given n students in the class like football, what may 2n show? What may — show?(Hint: Think of games other than football).
Solution.
(a) (x – 2) may show the age is Munnu’s younger brother. (a + 4) may show the age of Munnu’s elder brother. (3a+ 7) may show the age of Munnu’s grand mother.
(b) y + l indicates her age 7 years from now.
y – 3 indicates her age 3 years back.
y+ 4\(\frac { 1 }{ 2 } \) indicates her age 4\(\frac { 1 }{ 2 } \) years from now
y-2\(\frac { 1 }{ 2 } \) indicates her age 2\(\frac { 1 }{ 2 } \) years back.
(c) 2n may show the number of students who like cricket.
\(\frac { n }{ 2 } \)may show the number of students who like hockey.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4 help you. If you have any query regarding. NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4, drop a comment below and we will get back to you at the earliest.