RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20A

RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C

Question 1.
Solution:
(i)

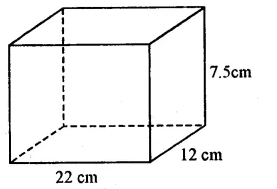
Length of cuboid (l) = 22 cm.
Breadth (b) = 12 cm
and height (h) = 7.5 cm.

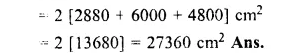
Question 2.
Solution:
Length of water tank (l) = 2 m
75cm = 2.75 m
breadth (b) = 1 m 80cm = 1.80 m
and height (h) = 1 m 40 cm = 1.40 m
Volume of water filled in it = l.b.h = 2.75 x 1.80 x 1.40 m³
= 6.93 m³
Water in litres = 6.93 x 1000
= 6930 litres (1 m³ = 1000 litres) Ans.

Question 3.
Solution:
Length of iron (l) = 1.05 m
= 105 cm
breadth (b) = 70 cm and height (h) = 1.5 cm
volume of iron = l x b x h = 105 x 70 x 1.5 cm³
= 11025 cm³
weight of 1cm³ iron = 8 gram
Total weight = 11025 x g = 88200 g
= \(\\ \frac { 88200 }{ 1000 } \) kg
= 88.2 kg Ans.

Question 4.
Solution:
Area of courtyard = 3750 m²
Height of gravel = 1 cm.
Volume of gravel = 3750 x \(\\ \frac { 1 }{ 100 } \) m³
= 37.50 m³
Cost of 1 m³ gravel = Rs. 6.40
Total cost = Rs. 6.40 x 37.50
= Rs. 240 Ans.

Question 5.
Solution:
Length of hall (l) = 16 m
Breadth (b) = 12.5 m
height (h) = 4.5 m
Volume of air in it = l x b x h
= 16 x 12.5 x 4.5 m3
= 900 m³
Air for one person is required = 3.6 m³
Number of person which can be accommodated in the hall = 900 ÷ 3.6
= \(\\ \frac { 900\times 10 }{ 36 } \)
= 250

Question 6.
Solution:
Length of cardboard box (l)
= 1.2 m = 120 cm.
breadth (b) = 72 cm.
Height (h) = 54 cm.
Volume of box = l x b x h
= 120 x 72 x 54 cm³
= 466560 cm³
Volume of one soap bar = 6 x 4.5 x 4 cm³
= 108 cm³
No. of bars to be kept in it = \(\\ \frac { 466560 }{ 108 } \)
= 4320 Ans.

Question 7.
Solution:
Volume of one match box = 4 x 2.5 x 1.5 cm³ = 15 cm³
Volume of 144 matchboxes = 15 x 144 cm³
or volume of one packet = 2160 cm³
Length of carton (l) = 1.5 m = 150 cm
Breadth (b) = 84 cm
and height (h) = 60 cm.
Volume of one carton = l x b x h
= 150 x 84 x 60 cm³
= 756000 cm³
No. of packets = 756000 ÷ 2160
= 350 Ans.

Question 8.
Solution:
Length of one plank = 2m
= 200 cm
Breadth (b) = 25 cm

Question 9.
Solution:
Length of wall (l) = 8m = 800 cm
Height (h) = 5.4 m = 540 cm
Width (b) = 33 cm

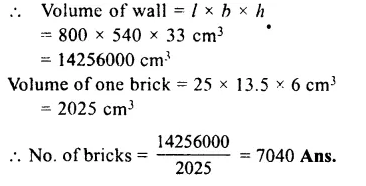
Question 10.
Solution:
Length of wall (l) = 15 m
Width (b) = 30 cm = 0.3 m
Height (h) = 4 m

Question 11.
Solution:
Length of rectangular cistern (l) = 11.2 m
Breadth (b) = 6 m
Height (h) = 5.8 m

Question 12.
Solution:
Volume of block of gold = 0.5 m³
= 0.5 x 1000000 cm³
= 500000 cm³

Question 13.
Solution:
Area of field = 2 hectare
= 20000 m²
Rainfall = 5 cm. = 0.05 m
Volume of water of rainfall
= Area of field x height of rainfall water
= 20000 x 0.05 m³
= 1000 m³ Ans.

Question 14.
Solution:
Speed of water = 3 km/h
Length of water flow in 1 minute
= \(\\ \frac { 3km }{ 60m } \)
= \(\\ \frac { 3000 }{ 60 } \)
= 50 m
Width of river = 45 m
Depth of river = 2 m
Volume of water in 1 minute
= 45 x 2 x 50 m³
= 4500 m³ Ans.

Question 15.
Solution:
Length of pit (l) = 5m
Width (b) = 3.5 m
Let depth of pit = h
then volume of earth dug out
= l.b.h = 5 x 3.5 x h = 17.5 h m³
But volume of earth = 14 m³
17.5 h = 14
h = \(\\ \frac { 14 }{ 17.5 } \) = \(\\ \frac { 140 }{ 175 } \)
=> h = \(\\ \frac { 4 }{ 5 } \) m
= \(\\ \frac { 4 }{ 5 } \) x 100
= 80 cm Ans.

Question 16.
Solution:
Width of tank = 90 cm = \(\\ \frac { 90 }{ 100 } \) m
Depth = 40 cm = \(\\ \frac { 40 }{ 100 } \) m
Water = 576 litre

Question 17.
Solution:
Volume of wood = 1.35 m³
Length of beam = 5m
Thickness = 36 cm = \(\\ \frac { 36 }{ 100 } \) m.
Width = \(\\ \frac { Volume }{ length\times thickness } \)

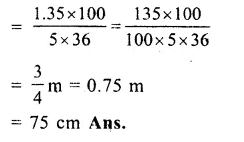
Question 18.
Solution:
Volume of a room = 378 m³
Area of its floor = 84 m²
Height = \(\\ \frac { Volume }{ Area } \)
= \(\\ \frac { 378 }{ 84 } \) m
= 4.5 m Ans.

Question 19.
Solution:
Length of pool = 260 m
and width = 140 m.
Volume of water = 54600 m³

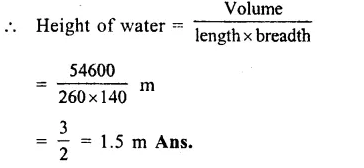
Question 20.
Solution:
Outer length of wooden box (L) = 60 cm
Width (B) = 45 cm
and height (H) = 32 cm.
Thickness of wood used = 2.5 cm.
Inner length (l) = 60 – 2 x 2.5
= 60 – 5
= 55 cm

Question 21.
Solution:
Outer length of open box = 36 cm
breadth = 25 cm
and height = 16.5 cm
thickness of iron = 1.5 cm.
∴ Inner length = 36 – 2 x 1.5
= 36 – 3
= 33 cm
breadth = 25 – 2 x 1.5
= 25 – 3
= 22 cm
and height = 16.5 – 1.5
= 15 cm .
∴ Volume of iron used in it = Outer volume – Inner volume
= 36 x 25 x 16.5 cm3 – 33 x 22 x 15 cm³
= 14850 – 10890
= 3960 cm³
weight of 1 cm³ = 8.5 gram
∴ Total weight = 3960 x 8.5 g
= 33660 g
= 33.660 kg
= 33.66 kg Ans.

Question 22.
Solution:
Outer length of the box = 56 cm
Width = 39 cm
and height = 30 cm
Volume = 56 x 39 x 30
= 65520 cm³
Thickness of wood used = 3cm.
∴ Inner length = 56 – 2 x 3
= 56 – 6
= 50 cm
Width = 39 – 2 x 3
= 39 – 6
= 33 cm
and height = 30 – 2 x 3
= 30 – 6
= 24 cm
∴ Inner volume of the box = 50 x 33 x 24 cm³
= 39600 cm³
and volume of wood used = Outer volume – Inner volume
= (65520 – 39600)cm³
= 25920 cm³ Ans.

Question 23.
Solution:
Outer length of box = 62 cm.
Outer width = 30 cm.
Outer height = 18 cm.
Thickness of wood = 2 cm.
∴ Internal length = 62 – 2 x 2
= 58 cm.
Internal width = 30 – 2 x 2
= 26 cm.
Internal height =18 – 2 x 2
= 14 cm.
Capacity of the box = lbh
= 58 x 26 x 14 cm³
= 21112 cm³ Ans.

Question 24.
Solution:
Outer length = 80 cm.
Outer width = 65 cm.
Outer height = 45 cm.
Total volume = 80 x 65 x 45 cm³
= 234000 cm³
Thickness of wood = 2.5 cm.
∴ Inner length = 80 – 2 x 2.5 = 75 cm.
Inner width = 65 – 2 x 2.5 = 60 cm.
Inner height = 45 – 2 x 2.5 = 40 cm.

Question 25.
Solution:
(i) Edge of cube (a) = 7 m

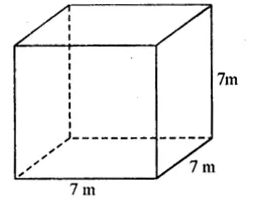
(a) Volume = a³ = (7)³
= 7 x 7 x 7 m³
= 343 m³ Ans.

Question 26.
Solution:
Surface area of a cube = 1176 cm²
Let edge of the cube = a

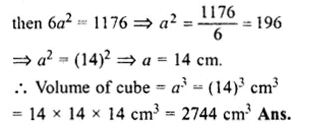
Question 27.
Solution:
Volume of a cube = 729 cm³
Let edge of cube = a
then a³ = 729 = (9)³
a = 9 cm.
Hence surface area = 6a² = 6 (9)² cm²
= 6 x 81
= 486 cm² Ans.

Question 28.
Solution:
Length of metal block (l) = 2.25 m = 225 cm
Width (b) = 1.5 m = 150 cm
and height (h) = 27 cm
Volume of block = l x b x h
= 225 x 150 x 27 cm³
= 911250 cm³
Side of each cube = 45 cm.
Volume of each cube = a³
= 45 x 45 x 45
= 94125 cm³
Number of cubes = \(\\ \frac { 911250 }{ 91125 } \)
= 10 Ans.

Question 29.
Solution:
Let edge of given cube = a
Volume = a³
and surface area = 6a²
By doubling the edge of cube3 the side of new cube = a x 2 = 2a
Volume (2a)³ = 8a³
and surface area = 6 (2a)² = 6 x 4a²
= 24a² = 4 x 6a²
It is clear from the above that
Volume is increased 8 times and surface area is 4 times. Ans.

Question 30.
Solution:
Total cost of wood = Rs. 256
Rate = Rs.,500 per m³
Volume of wood = \(\\ \frac { 256 }{ 500 } \) = 0.512 m³
= 0.512 x 100 x 100 x 100 cm³
= 512000 cm³
Let length of each side = a
then a³ = 512000 = (80)³
a = 80
Hence length of each side = 80 cm. Ans.

 

Hope given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.