RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20B

RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C

Question 1.
Solution:
(i) Radius of the base of the cylinder (r) = 7 cm.
Height (h) = 50 cm.

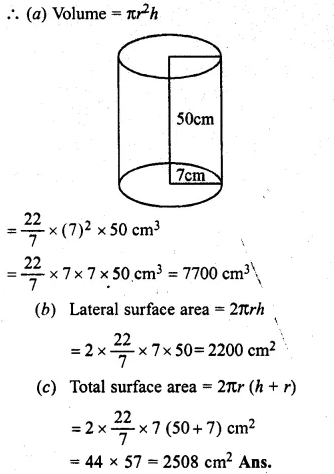
Question 2.
Solution:
Radius of cylindrical tank (r) = 1.5 m
and height (h) = 10.5 m

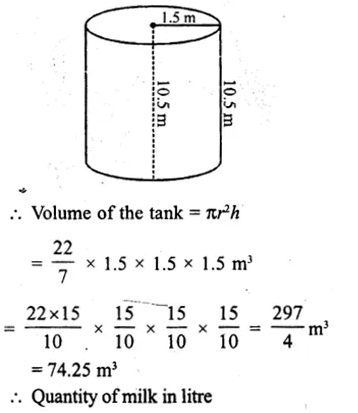
= 74.25 x 1000l
= 74250 l

Question 3.
Solution:
Radius of the base of pole (r)
= 10 dm
= \(\\ \frac { 10 }{ 100 } \) m
= \(\\ \frac { 1 }{ 10 } \) m

Question 4.
Solution:
Volume of cylinder = 1.54 m³
= 1540000 cm³
Diameter of its base = 140 cm
Radius (r) = 70 cm

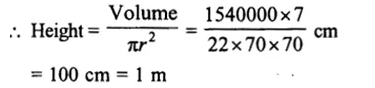
Question 5.
Solution:
Volume of cylindrical rod = 3850 cm³
Length of rod (h) = 1 m = 100 cm
Let radius of the base of the rod = r

Question 6.
Solution:
Diameter of closed cylinder = 14 m
Radius = \(\\ \frac { 14 }{ 2 } \)
= 7 m
Height = 5

Question 7.
Solution:
Circumference of the base of cylinder = 88 cm.

Question 8.
Solution:
Lateral surface of cylinder = 220 m²
Height (h) = 14 m
Let radius of cylinder = r

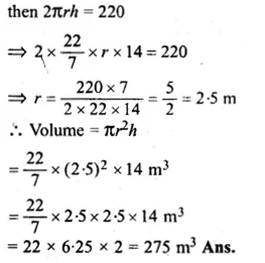
Question 9.
Solution:
Volume of cylinder = 1232 cm³
height (h) = 8cm
Let r be the radius, then

Question 10.
Solution:
Ratio in radius and height of a cylinder = 7 : 2
Let radius = 7x
then height = 2x

Question 11.
Solution:
Curved surface area = 4400 cm²
circumference of base = 110 cm
Let r be the radius

Question 12.
Solution:
In first case,
Side of square base (a) = 5 cm.
and height (h) = 14 cm.
Volume = 5 x 5 x 14 = 350 cm³
In second case,
Radius of the circular base (r) = 3.5 cm.
Height (h) = 12 cm.
Volume = πr²h
= \(\\ \frac { 22 }{ 7 } \) x 3.5 x 3.5 x 12 cm³
= 462 cm²
Hence second type of circular plastic can has greater capacity.
Difference = 462 – 350
= 112 cm³

Question 13.
Solution:
Diameter of a cylindrical pillar = 48 cm.
Radius (r) = \(\\ \frac { 48 }{ 2 } \) = 24 cm.
\(\\ \frac { 24 }{ 100 } \) m

Question 14.
Solution:
Length of rectangular vessel (l) = 22 cm.
Breadth (A) = 16 cm.
and height (A) = 14 cm.

Question 15.
Solution:
Diameter of cylindrical metal = 1 cm.
Radius (r) = \(\\ \frac { 1 }{ 2 } \) cm.
Length. (A) = 11 cm.
Volume = πr²h

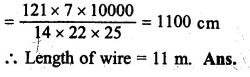
Question 16.
Solution:
Side of a solid cube = 2.2 cm
Volume = (side)³
= (2.2)³
= 10.648 cm³

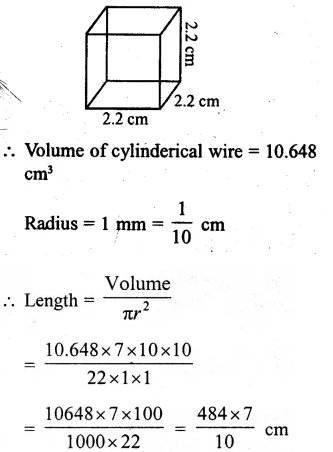
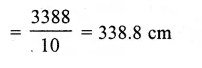
Question 17.
Solution:
Diameter of a well = 7 m
Radius (r) = \(\\ \frac { 7 }{ 2 } \) m

Question 18.
Solution:
Inner diameter of well = 14 m
Inner radius = \(\\ \frac { 14 }{ 2 } \) = 7 m
Depth (h) = 12 m

Question 19.
Solution:
No. of revolutions = 750
Diameter of road roller = 84 cm
Length (h) = 1 m

Question 20.
Solution:
Thickness of the metal = 1.5 cm.
External diameter = 12 cm.

Question 21.
Solution:
Inner diameter of tube = 12 cm.
Inner radius (r) = \(\\ \frac { 12 }{ 2 } \) = 6 cm.
Thickness of metal = 1 m.

Hope given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.