RD Sharma Class 8 Solutions Chapter 20 Mensuration I (Area of a Trapezium and a Polygon) Ex 20.2
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2
Other Exercises
- RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1
- RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2
- RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3
Question 1.
Find the area, in square metres, of the trapezium whose bases and altitude are as under:
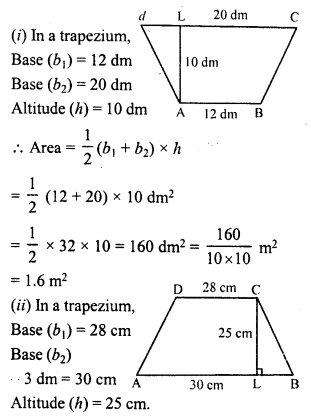
(i) bases = 12 dm and 20 dm, altitude =10 dm
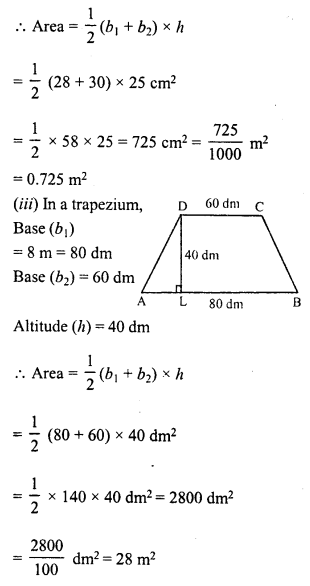
(ii) bases = 28 cm and 3 dm, altitude = 25 cm
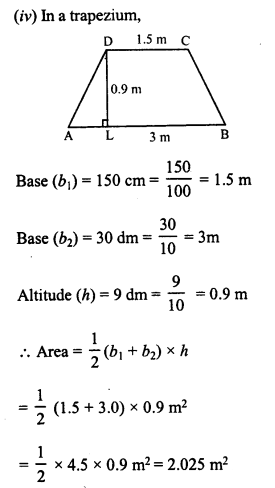
(iii) bases = 8 m and 60 dm, altitude = 40 dm
(iv) bases = 150 cm and 30 dm, altitude = 9 dm
Solution:
Question 2.
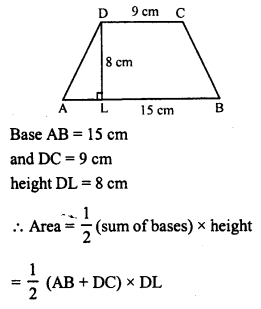
Find the area of trapezium with base 15 cm and height 8 cm. If the side parallel to the given base is 9 cm long.
Solution:
In the trapezium ABCD,
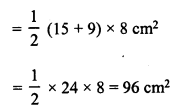
Question 3.
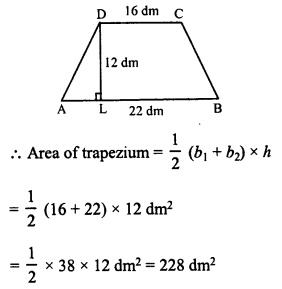
Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
Solution:
Length of parallel sides of a trapezium are 16 dm and 22 dm i.e.
b1 = 16 dm, b2 = 22 dm
and height (h) = 12 dm
Question 4.
Find the height of a trapezium, the sum of lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm²
Solution:
Sum of parallel sides (b1 + b2) = 60 cm
Area of trapezium = 600 cm²

Question 5.
Find the altitude of a trapezium whose area is 65 cm² and whose bases are 13 cm and 26 cm.
Solution:
Area of a trapezium = 65 cm²
Bases are 13 cm and 26 cm
i.e. b1 = 13 cm, b2 = 26 cm.

Question 6.
Find the sum of the lengths of the bases of trapezium whose area is 4.2 m² and whose height is 280 cm.
Solution:
Area of trapezium = 4.2 m²
Height (h) = 280 cm = 2.8 m.

Question 7.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate the area as
(i) the sum of the areas of two triangles and one rectangle.
(ii) the difference of the area of a rectangle id the sum of the areas of two triangles.
Solution:
In trapezium ABCD, parallel sides or bases are 10 cm and 15 cm and height = 6 cm
Area of trapezium
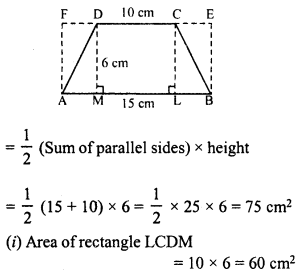

Area of trapezium = 90 – 15 = 75 cm²
= area of rectangle – areas of two triangles.
Question 8.
The area of a trapezium is 960 cm². If the parallel sides are 34 cm and 46 cm, find the distance between them:
Solution:
Area of trapezium = 960 cm²
Parallel sides are 34 cm and 46 cm
b1 + b2 = 34 + 46 = 80 cm
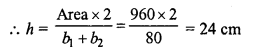
Distance between parallel sides = 24 cm
Question 9.
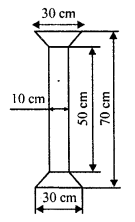
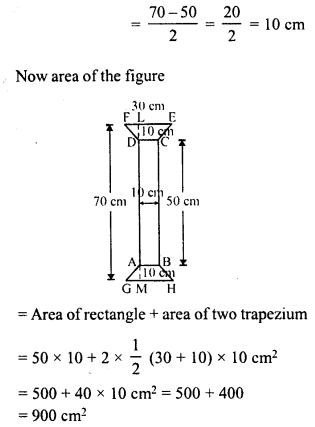
Find the area of the figure as the sum of the areas of two trapezium and a rectangle.
Solution:
In the figure,
One rectangle is ABCD whose sides are 50 cm and 10 cm.
Two trapezium of equal size in which parallel sides are 30 cm and 10 cm and height
Question 10.
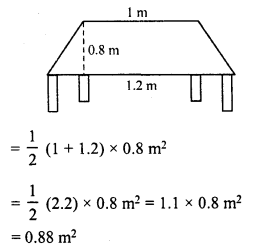
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
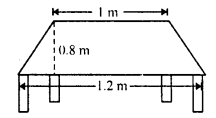
Solution:
Top of a table is of trapezium in shape whose parallel sides are 1 m and 1.2 m and distance between them (h) = 0.8 m
Area of trapezium = \(\frac { 1 }{ 2 }\) (Sum of parallel sides) x height
Question 11.
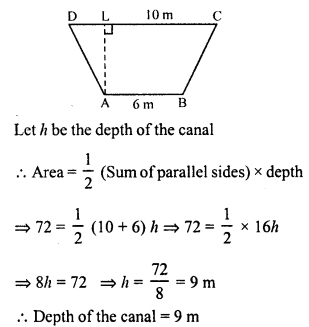
The cross-section of a canal is a trapezium in shape. If the canal is 10 m wide at the top 6 m wide at the bottom, and the area of the cross-section is 72 m², determine its depth.
Solution:
Area of cross-section = 72 m²
Parallel sides of the trapezium = 10 m and 6 m
Question 12.
The area of a trapezium is 91 cm² and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
Solution:
Area of trapezium = 91 cm²
Height (h) = 7 cm.
Sum of parallel sides
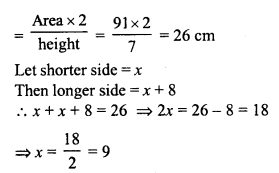
One parallel side = 9 cm
and second side = 9 + 8 = 17 cm
Hence parallel sides are 17 cm, 9 cm
Question 13.
The area of a trapezium is 384 cm². Its parallel sides are in the ratio 3 : 5 and the perpendicular distance between them is 12 cm. Find the length of each one of the parallel sides.
Solution:
Area of trapezium = 384 cm²
Perpendicular distance (h) = 12 cm
Sum of parallel sides

First parallel side = 8 x 3 = 24 cm
Second side = 8 x 5 = 40 cm
Question 14.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel and twice the side along the road. If the area of this field is 10500 m² and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
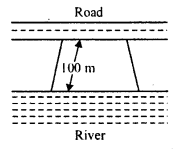
Solution:
Area of the trapezium shaped field = 10500 m²
and perpendicular distance between them (h) = 100 m.

Question 15.
The area of trapezium is 1586 cm² and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
Solution:
Area of a trapezium = 1586 cm²
and distance between the parallel sides (h) = 26

Question 16.
The parallel sides of a trapezium are 25 cm and 13 cm ; Its nonparallel sides are equal each being 10 cm, find the area of the trapezium.
Solution:
Parallel sides of a trapezium ABCD are 25 cm and 13 cm
i.e. AB = 25 cm, CD = 13 cm
and each non-parallel side = 10 cm
i.e., AD = BC = 10 cm
From C, draw CE || DA and draw CL ⊥ AB
CE = DA = CB = 10 cm
and EB = AB – AE = AB – DC = 25 – 13 = 12 cm
Perpendicular CL bisects base EB of an isosceles ∆CED

Question 17.
Find the area of a trapezium whose parallel sides are 25 cm, 13 cm and other sides are 15 cm each.
Solution:
In trapezium ABCD, parallel sides are AB and DC.
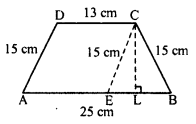
AB = 25 cm, CD = 13 cm
and other sides are 15 cm each i.e. AD = CB = 15 cm
From C, draw CE || DA and CL ⊥ AB
AE = DC = 13 cm
and EB = AB – AE = 25 – 13 = 12 cm
Perpendicular CL bisects the base EB of the isosceles triangle CEB

Question 18.
If the area of a trapezium is 28 cm² and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
Solution:
Area of trapezium = 28 cm²
Altitude (h) = 4 cm.

One of the parallel side = 6 cm
Second parallel side = 14 – 6 = 8 cm
Question 19.
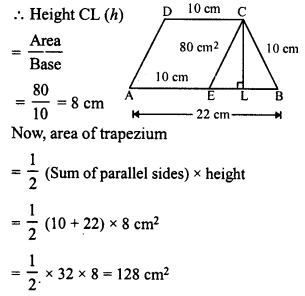
In the figure, a parallelogram is drawn in a trapezium the area of the parallelogram is 80 cm², find the area of the trapezium.
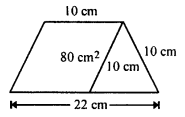
Solution:
Area of parallelogram (AECD) = 80 cm²
Side AE (b) = 10 cm
Question 20.
Find the area of the field shown in the figure by dividing it into a square rectangle and a trapezium.
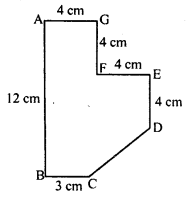
Solution:
Produce EF to H to meet AB at H and draw DK || EH
HF = 4 cm, KD = HE = 4 + 4 = 8 cm
HK = ED = 4 cm,
KB = 12 – (8) = 4 cm
Now, area of square AGFH = 4 x 4 = 16 cm²
area of rectangle KDEH = l x b = 8 x 4 = 32 cm²
and area of trapezium BCDK.
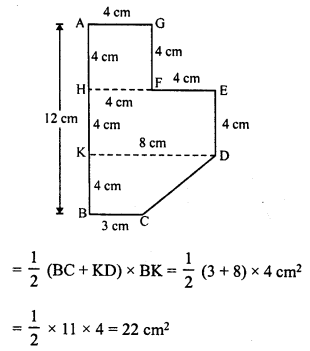
Total area of the figure = 16 + 32 + 22 = 70 cm²
Hope given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.