RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1

RD Sharma Class 8 Solutions Chapter 20 Mensuration I (Area of a Trapezium and a Polygon) Ex 20.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3

Question 1.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m² ?
Solution:
Area of floor = 1080 m²
Base of parallelogram shaped tile (b) = 24 cm
and corresponding height (h) = 10 cm
Area of one tile = b x h = 24 x 10 = 240 cm²

Question 2.
A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Fig. If AB = 60 m and BC = 28 m, find the area of the plot.

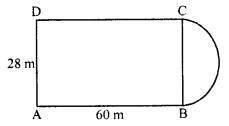
Solution:
Length of rectangular portion (l) = 60 m
and breadth (b) = 28 m
Area of the rectangular plot = l x b = 60 x 28 m² = 1680 m²
Radius of semicircular portion (r) = \(\frac { b }{ 2 }\) = \(\frac { 28 }{ 2 }\) = 14 m
Area = \(\frac { 1 }{ 2 }\) πr²
= \(\frac { 1 }{ 2 }\) x \(\frac { 22 }{ 7 }\) x 14 x 14 m²
= 308 m²
Total area of the plot = 1680 + 308 = 1988 m²

Question 3.
A playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π = \(\frac { 22 }{ 7 }\)).
Solution:
Length of rectangular portion (l) = 36 m
and breadth (b) = 24.5 m

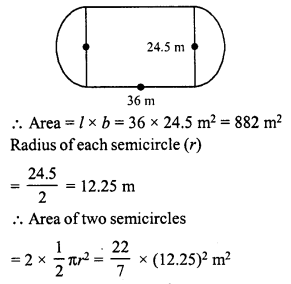
= \(\frac { 22 }{ 7 }\) x 150.0625 m²
= 471.625 m²
Total area of the playground = 471.625 + 882 = 1353.625 m²

Question 4.
A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 have been cut. Find the area of the remaining part.
Solution:
Length of rectangular piece (l) = 20 m
breadth (b) = 15 m

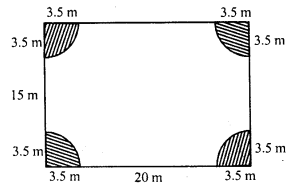
Area of rectangular piece = l x b = 20 x 15 = 300 m²
Radius of each quadrant (r) = 3.5 m
Total area of 4 quadrants

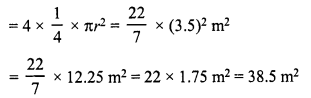
Area of the remaining portion = 300 – 38.5 m² = 261.5 m²

Question 5.
The inside perimeter of a running track (shown in Fig.) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

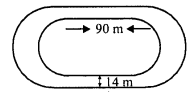
Solution:
Inner perimeter = 400 m.
Length (l) = 90 m.
Perimeter of two semicircles = 400 – 2 x 90 = 400 – 180 = 220 m

Question 6.
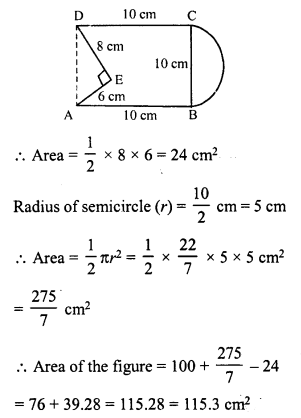
Find the area of the Figure in square cm, correct to one place of decimal. (Take π = \(\frac { 22 }{ 7 }\))

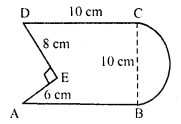
Solution:
Length of square (a) = 10 cm.
Area = a² = (10)² = 100 cm²
Base of the right triangle AED = 8 cm
and height = 6 cm

Question 7.
The diameter of a wheel of a bus is 90 cm which makes 315 revolutions per minute. Determine its speed in kilometres per hour. (Take π = \(\frac { 22 }{ 7 }\))
Solution:
Diameter of the wheel (d) = 90 cm.

Question 8.
The area of a rhombus is 240 cm² and one of the diagonal is 16 cm. Find another diagonal.
Solution:
Area of rhombus = 240 cm²
Length of one diagonal (d₁) = 16 cm
Second diagonal (d₂)

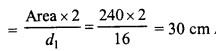
Question 9.
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution:
In rhombus, diagonal (d₁) = 7.5 cm
and diagonal (d₂) = 12 cm

Question 10.
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Solution:
In quadrilateral shaped field ABCD,
diagonal AC = 24 m

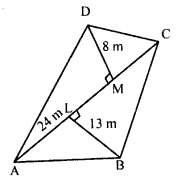
and perpendicular BL = 13 m
and perpendicular DM on AC = 8 m
Area of the field ABED = \(\frac { 1 }{ 2 }\) x AC x (BL + DM)
= \(\frac { 1 }{ 2 }\) x 24 x (13 + 8) m²
= 12 x 21 = 252 m²

Question 11.
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Solution:
Side of rhombus (b) = 6 cm
Altitude (h) = 4 cm

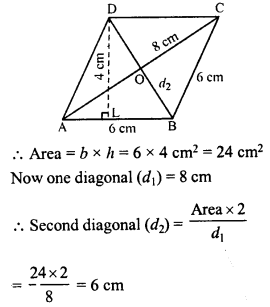
Question 12.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is Rs 4.
Solution:
Number of rhombus shaped tiles = 300
Diagonals of each tile = 45 cm and 130 cm

Rate of polishing the tiles = Rs 4 per m²
Total cost = 202.5 x 4 = Rs 810

Question 13.
A rectangular grassy plot is 112 m long and 78 broad. It has a gravel path 2.5 m wide all around it on the side. Find the area of the path and the cost of constructing it at Rs 4.50 per square metre.
Solution:
Length of rectangular plot (l) = 112 m
and breadth (b) = 78 m
Width of path = 2.5 m

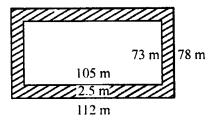
Inner length = 112 – 2 x 2.5 = 112 – 5 = 107 m
and inner breadth = 78 – 2 x 2.5 = 78 – 5 = 73 m
Area of path = outer area – inner area
= (112 x 78 – 107 x 73) m² = 8736 – 7811 = 925 m²
Rate of constructing = Rs 4.50 per m²
Total cost = 925 x Rs 4.50 = Rs 4162.50

Question 14.
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
Solution:
Side of rhombus = 20 cm.
One diagonal (d₁) = 24 cm

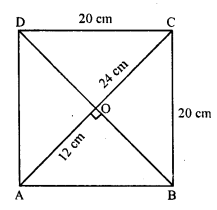
Diagonals of a rhombus bisect each other at right angle
AB = 20 cm
and OA = \(\frac { 1 }{ 2 }\) AC = \(\frac { 1 }{ 2 }\) x 24 cm = 12 cm
In right-angled ∆AOB,
AB² = AO² + BO² (Pythagoras theorem)
⇒ (20)² = (12)² + BO²
⇒ 400 = 144 + BO²
⇒ BO² = 400 – 144 = 256 = (16)²
⇒ BO = 16 cm
and diagonal BD = 2 x BO = 2 x 16 = 32 cm
Now area of rhombus ABCD

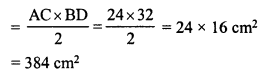
Question 15.
The length of a side of a square field is 4 m. What will be the altitude of the rhombus if the area of the rhombus is equal to the square field and one of its diagonal is L m ?
Solution:
Side of square = 4 m
Area of square = (a)² = 4 x 4 =16 m²

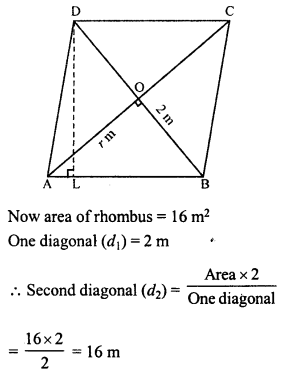
Diagonals of a rhombus bisect each other at right angles.
In right ∆AOB
AB² = QA² + BO² (Pythagoras theorem)
= (8)² + (1)² = 64 + 1 = 65
AB = √65 m.
Now, length of perpendicular AL (h)

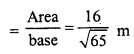
Question 16.
Find the area of the field in the form of a rhombus, if the length of each side be 14 cm and the altitude be 16 cm.
Solution:
Length of each side of rhombus = 14 cm.
Length of altitude = 16 cm
Area = Base x altitude = 14 x 16 cm² = 224 cm²

Question 17.
The cost of fencing a square field at 60 paise per metre is Rs 1,200. Find the cost of reaping the field at the rate of 50 paise per 100 sq. metres.
Solution:
Cost of fencing the square field = Rs 1,200
Rate = 60 paise per m.

Question 18.
In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.
Solution:
Side of a square plot = 84 m
Area = (a)² = (84)² = 84 x 84 m² = 7056 m²
Area of rectangular field = 7056 m²
Length (l) = 144 m

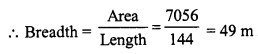
Question 19.
The area of a rhombus is 84 m². If its perimeter is 40 m, then find its altitude.
Solution:
Area of rhombus = 84 m²
Perimeter = 40 m

Question 20.
A garden is in the form of a rhombus whose side is 30 metres and the corresponding altitude is 16 m. Find the cost of levelling the garden at the rate of Rs 2 per m².
Solution:
Side of rhombus garden (b) = 30 m.
Altitude (h) = 16 m
Area = Base x altitude = 30 x 16 = 480 m²
Rate of levelling the garden = Rs 2 per m²
Total cost = Rs 480 x 2 = Rs 960

Question 21.
A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus ?
Solution:
Length of side of rhombus (b) = 64 m
and altitude (h) = 16 m
Area = b x h = 64 x 16 m² = 1024 m²
Now area of square = 1024 m²
Side of the square = √Area = √1024 m = 32 m

Question 22.
The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are 24.8 cm and 16.5 cm respectively. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.
Solution:
Base of triangle (b) = 24.8 cm
and altitude (h) = 16.5 cm
Area of triangle = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x bh= \(\frac { 1 }{ 2 }\) x 24.8 x 16.5 cm² = 204.6 cm²
Area of rhombus = 204.6 cm²
Length of one diagonal (d₁ = 22 cm
Second diagonal (d₂)

 

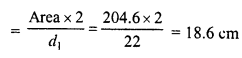
Hope given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.