Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

Solve equations, number 1 to number 20, given below, using factorisation method :
Question 1.
x² – 10x – 24 = 0
Solution:
x² – 12x + 2x – 24 = 0
⇒ x (x – 12) + 2 (x – 12) = 0
⇒ (x – 12) (x + 2) = 0
Either x – 12 = 0, then x = 12
or x + 2 = 0, then x = – 2
x = 12, – 2

Question 2.
x² – 16 = 0
Solution:
⇒ x² – (4)² = 0
⇒ (x + 4) (x – 4) = 0
Either x + 4 = 0, then x = – 4
or x – 4 = 0, then x = 4
x = 4, – 4

Question 3.
2x² – \(\frac { 1 }{ 2 }\) x = 0
Solution:
⇒ 4x² – x = 0
⇒ x (4x – 1) = 0
Either x = 0,
or 4x – 1 = 0, then 4x = 1 ⇒ x = \(\frac { 1 }{ 4 }\)
x = 0, \(\frac { 1 }{ 4 }\)

Question 4.
x (x – 5) = 24
Solution:
⇒ x² – 5x – 24 = 0
⇒ x² – 8x + 3x – 24 = 0
⇒ x (x – 8) + 3 (x – 8) = 0
⇒ (x – 8) (x + 3) = 0
Either x – 8 = 0, then x = 8
or x + 3 = 0, then x = – 3
x = 8, – 3

Question 5.
\(\frac { 9 }{ 2 }\) x = 5 + x²
Solution:
⇒ 9x = 10 + 2x²
⇒ 2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2x – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
x = 2, \(\frac { 5 }{ 2 }\)

Question 6.
\(\frac { 6 }{ x }\) = 1 + x
Solution:
⇒ 6 = x + x²
⇒ x² + x – 6 = 0
⇒ x² + 3x – 2x – 6 = 0
⇒ x (x + 3) – 2 (x + 3) = 0
⇒ (x + 3) (x – 2) = 0
Either x + 3 = 0, then x = – 3
or x – 2 = 0, then x = 2
x = 2, – 3

Question 7.
x = \(\frac { 3x + 1 }{ 4x }\)
Solution:
⇒ 4x² = 3x + 1
⇒ 4x² – 3x – 1 = 0
⇒ 4x² – 4x + x – 1 = 0
⇒ 4x (x – 1) + 1 (x – 1) = 0
⇒ (x – 1) (4x + 1) = 0
Either x – 1 = 0, then x = 1
or 4x + 1 = 0, then 4x = -1 ⇒ x = \(\frac { -1 }{ 4 }\)
x = 1, \(\frac { -1 }{ 4 }\)

Question 8.
x + \(\frac { 1 }{ x }\) = 2.5
Solution:

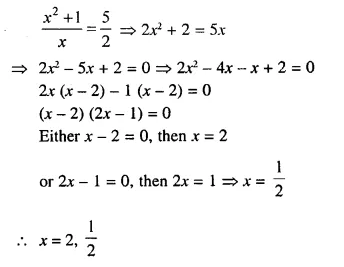
Question 9.
(2x – 3)² = 49
Solution:
⇒ 4x² – 12x + 9 = 49
⇒ 4x² – 12x + 9 – 49 = 0
⇒ 4x² – 12x – 40 = 0
⇒ x² – 3x – 10 = 0 (Dividing by 4)
⇒ x² – 5x + 2x – 10 = 0
⇒ x (x – 5) + 2 (x – 5) = 0
⇒ (x – 5) (x + 2) = 0
Either x – 5 = 0, then x = 5
or x + 2 = 0, then x = – 2
x = 5, – 2

Question 10.
2 (x² – 6) = 3 (x – 4)
Solution:
⇒ 2x² – 12 = 3x- 12
⇒ 2x² – 3x – 12 + 12 = 0
⇒ 2x² – 3x = 0
⇒ x (2x – 3) = 0
Either A = 0,
or 2x – 3 = 0, then 2x = 3 ⇒ x = \(\frac { 3 }{ 2 }\)
x = 0, \(\frac { 3 }{ 2 }\)

Question 11.
(x + 1) (2x + 8) = (x + 7) (x + 3)
Solution:

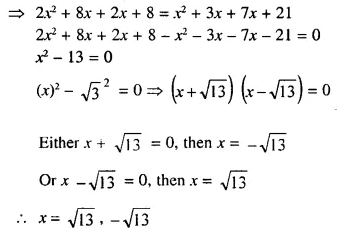
Question 12.
x² – (a + b) x + ab = 0
Solution:
⇒ x² – ax – bx + ab = 0
⇒ x (x – a) – b (x – a) = 0
⇒ (x – a) (x – b) = 0
Either x – a = 0, then x = a
or x – b = 0, then x = b
x = a, b

Question 13.
(x + 3)² – 4 (x + 3) – 5 = 0
Solution:
Let x + 3 = y, then
⇒ y² – 4y – 5 = 0
⇒y² – 5y + y – 5 = 0
⇒ y (y – 5) + 1 (y – 5) = 0
⇒ (y – 5) (y + 1) = 0
Substituting the value of y,
⇒ (x + 3 – 5) (x + 3 + 1) = 0
⇒ (x – 2) (x + 4) = 0
Either x – 2 = 0, then x = 2
or x + 4 = 0, then x = – 4
x = 2, -4

Question 14.
4 (2x – 3)² – (2x – 3) – 14 = 0
Solution:
Let 2x – 3 = y, then
⇒ 4y² – y – 14 = 0
⇒ 4y² – 8y + 7y – 14 = 0
⇒ 4y (y – 2) + 7 (y – 2) = 0
⇒ (y – 2) (4y + 7) = 0
Substituting the value of y,
⇒ (2x – 3 – 2) (8x – 12 + 7) = 0
⇒ (2x – 5) (8x – 5) = 0
Either 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
or 8x – 5 = 0, then 8x = 5 ⇒ x = \(\frac { 5 }{ 8 }\)
x = \(\frac { 5 }{ 2 }\) , \(\frac { 5 }{ 8 }\)

Question 15.

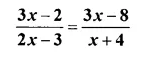
Solution:
⇒ (3x – 2) (x + 4) = (3x – 8) (2x – 3)
⇒ 3x² + 12x – 2x – 8 = 6x² – 9x – 16x + 24
⇒ 3x² + 12x – 2x – 8 – 6x² + 9x + 16x – 24 = 0
⇒ – 3x² + 35x – 32 = 0
⇒ 3x² – 35x + 32 = 0
⇒ 3x² – 3x – 32x + 32 = 0
⇒ 3x (x – 1) – 32 (x – 1) = 0
⇒ (x – 1) (3x – 32) = 0
⇒ 3x (x – 1) – 32 (x – 1) = 0
⇒ (x – 1) (3x – 32) – 0
Either x – 1 = 0, then x = 1
or 3x – 32 = 0, then 3x = 32 ⇒ x = \(\frac { 32 }{ 3 }\)
x = 1, \(\frac { 32 }{ 3 }\) or 1, 10\(\frac { 2 }{ 3 }\)

Question 16.
2x² – 9x + 10 = 0, when :
(i) x ∈ N
(ii) x ∈ Q.
Solution:
2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2 – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
(i) When x ∈ N, then x = 2
(ii) When x ∈ Q, then x = 2 , \(\frac { 5 }{ 2 }\)

Question 17.

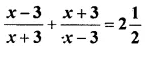
Solution:

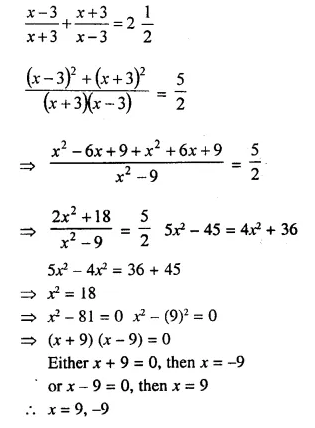
Question 18.

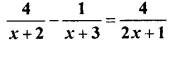
Solution:

Question 19.

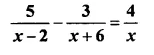
Solution:

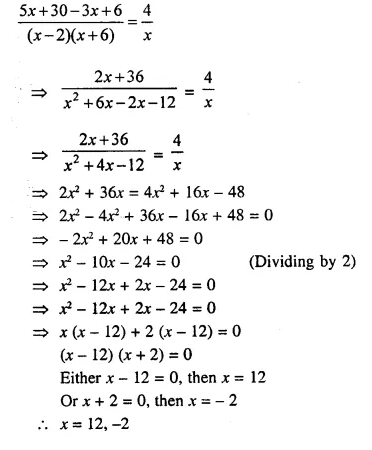
Question 20.

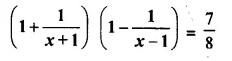
Solution:

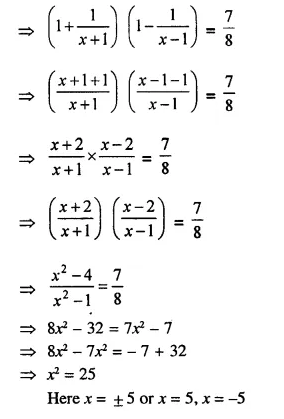
Question 21.
Find the quadratic equation, whose solution set is :
(i) {3, 5}
(ii) {-2, 3}
Solution:
(i) Solution set is {3, 5} or x = 3 and x = 5
Equation will be
(x – 3) (x – 5) = 0
⇒ x² – 5x – 3x + 15 = 0
⇒ x² – 8x + 15 = 0
(ii) Solution set is {-2, 3} or x = -2, x = 3
Equation will be
(x + 2) (x – 3) = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x² – x – 6 = 0

Question 22.

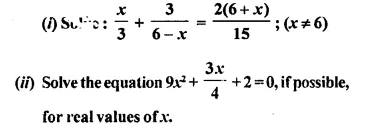
Solution:


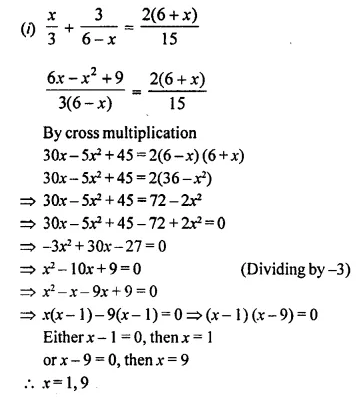
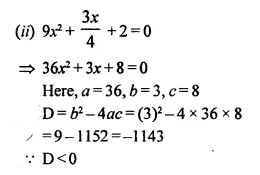
Roots are not real.
Hence there is no possible real value of x.

Question 23.
Find the value of x, if a + 1 = 0 and x² + ax – 6 = 0.
Solution:
a + 1 = 0 ⇒ a = -1
Now the equation x² + ax – 6 = 0 will be x² + (-1) x – 6 = 0
⇒ x² – x – 6 = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x (x – 3) + 2 (x – 3) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = – 2
x = 3, – 2

Question 24.
Find the value of x, if a + 7 = 0; b + 10 = 0 and 12x² = ax – b.
Solution:
a + 7 = 0, then a = -7
and b + 10 = 0, then b = -10
Now, substituting the value of a and b in
12x² = ax – b
⇒ 12x² = – 7x – (-10)
⇒ 12x² = – 7x + 10
⇒ 12x² + 7x – 10 = 0
⇒ 12x² + 15x – 8x – 10 = 0
⇒ 3x (4x + 5) – 2 (4x + 5) = 0
⇒ (4x + 5) (3x – 2) = 0
Either 4x + 5 = 0, then 4x = -5 ⇒ x = \(\frac { 5 }{ 4 }\)
or 3x – 2 = 0, then 3x = 2 ⇒ x = \(\frac { 2 }{ 3 }\)
x = \(\frac { 5 }{ 4 }\), \(\frac { 2 }{ 3 }\)

Question 25.
Use the substitution y = 2x + 3 to solve for x, if 4 (2x + 3)² – (2x + 3) – 14 = 0.
Solution:
y = 2x + 3, then equation
4 (2x + 3)² – (2x + 3) – 14 = 0 will be 4y² – y – 14 = 0
⇒ 4y² – 8y + 7y – 14 = 0
⇒ 4y (y – 2) + 7 (y – 2) = 0
⇒ (y – 2) (4y + 7) = 0
Either y – 2 = 0, then y = 2

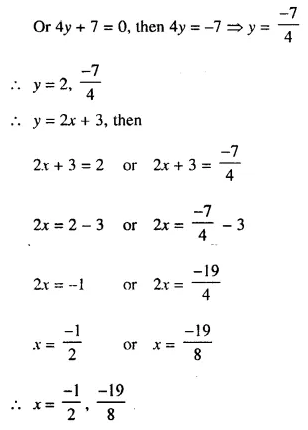
Question 26.
Without solving the quadratic equation 6x² – x – 2 = 0, find whether x = \(\frac { 2 }{ 3 }\) is a solution of this equation or not.
Solution:

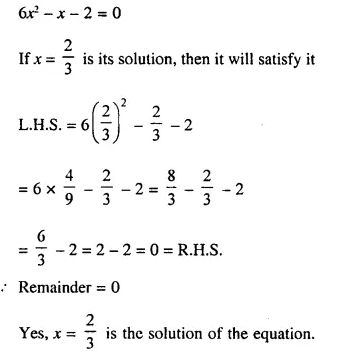
Question 27.
Determine whether x = -1 is a root of the equation x² – 3x + 2 = 0 or not.
Solution:
x² – 3x + 2 = 0
x = -1
Substituting the value of x = -1, in the quadratic equation
L.H.S. = x² – 3x + 2 = (-1)² – 3(-1) + 2 = 1 + 3 + 2 = 6 ≠ 0
Remainder is not equal to zero
x = -1 is not its root.

Question 28.
If x = \(\frac { 2 }{ 3 }\) is a solution of the quadratic equation 7x² + mx – 3 = 0; find the value of m.
Solution:

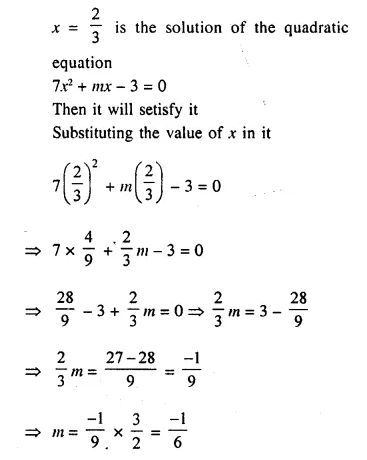
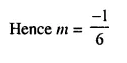
Question 29.
If x = -3 and x = \(\frac { 2 }{ 3 }\) are solutions of quadratic equation mx² + 7x + n = 0, find the values of m and n.
Solution:
x = -3, x = \(\frac { 2 }{ 3 }\) are the solution of the quadratic equation, mx² + 7x + n = 0
Then these values of x will satisfy it
(i) If x = -3, then mx² + 7x + n = 0
⇒ m(-3)² + 7(-3) + n = 0
⇒ 9m – 21 + n = 0
⇒ n = 21 – 9m ……(i)

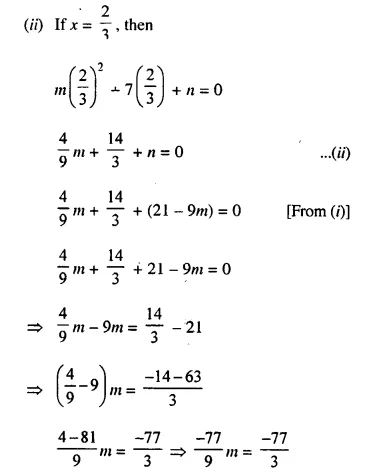
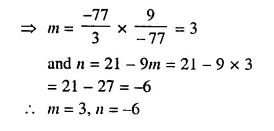
Question 30.
If quadratic equation x² – (m + 1) x + 6 = 0 has one root as x = 3; find the value of m and the other root of the equation.
Solution:
In equation, x² – (m + 1) x + 6 = 0
x = 3 is its root, then it will satisfy it
⇒ (3)² – (m + 1) x 3 + 6 = 0
⇒ 9 – 3m – 3 + 6 = 0
⇒ -3m + 12 = 0

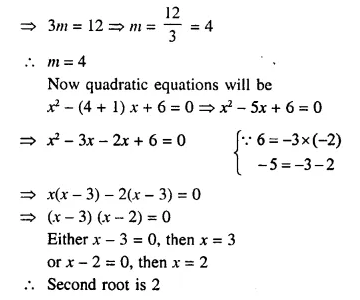
Question 31.
Give that 2 is a root of the equation 3x² – p (x + 1) = 0 and that the equation px² – qx + 9 = 0 has equal roots, find the values of p and q.
Solution:
3x² – p (x + 1) = 0
⇒ 3x² – px – p = 0
2 is a root of the equal It will satisfy it
3(2)² – p(2) – p = 0
⇒ 3 x 4 – 2p – p = 0
⇒ 12 – 3p = 0
⇒ 3p = 12
⇒ p = 4
px² – qx + 9 = 0
Here, a = p, b = -q, c = 9
D = b² – 4ac = (-q)² – 4 x p x 9 = q² – 36p
Roots are equal.
D = 0
⇒ q² – 36p = 0
⇒ q² – 36 x 4 = 0
⇒ q² = 144
⇒ q² = (±12)²
⇒ q = ± 12
Hence, p = 4 and q = ±12

Question 32.

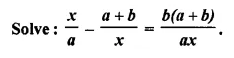
Solution:

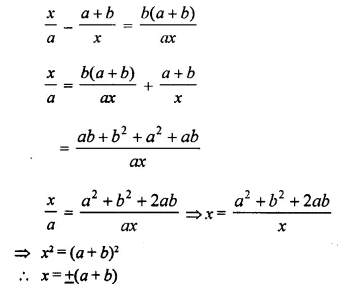
Question 33.
Solve: ( \(\frac { 1200 }{ x }\) + 2 ) (x – 10) – 1200 = 60
Solution:

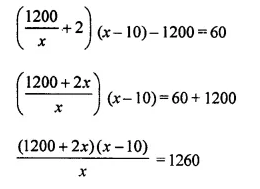
By cross multiplication,
⇒ 1200x – 12000 + 2x² – 20x – 1260x = 0
⇒ 2x² + 1200x – 20x – 1260x – 12000 = 0
⇒ 2x² – 80x – 12000 = 0
⇒ x² – 40x – 6000 = 0
⇒ x² – 100x + 60x – 6000 = 0
⇒ x (x – 100) + 60 (x – 100) = 0
⇒ (x – 100) (x + 60) = 0
Either x – 100 = 0, then x = 100
or x + 60 = 0, then x = -60
x = 100, -60

Question 34.
If -1 and 3 are the roots of x² + px + q = 0, find the values of p and q.
Solution:
-1 and 3 are the roots of the equation
x² + px + q = 0
Substituting the value of x = -1 and also x = 3, then
(-1 )² + p(-1) + q = 0
⇒ 1 – p + q = 0
⇒ p – q = 1
⇒ p = 1 + q …(i)
and (3)² + p x 3 + q = 0
⇒ 9 + 3p + q = 0
⇒ 9 + 3 (1 + q) + q = 0 [From(i)]
⇒ 9 + 3 + 3q + q = 0
⇒ 12 + 4q = 0
⇒ 4q = -12
⇒ q = -3
p = 1 + q = 1 – 3 = -2
Hence, p = -2, q = -3

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.