Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Question 1.
The 6th term of an A.P. is 16 and the 14th term is 32. Determine the 36th term.
Solution:
Let the first term and common difference of an A.P. be a and d
As, we know that,

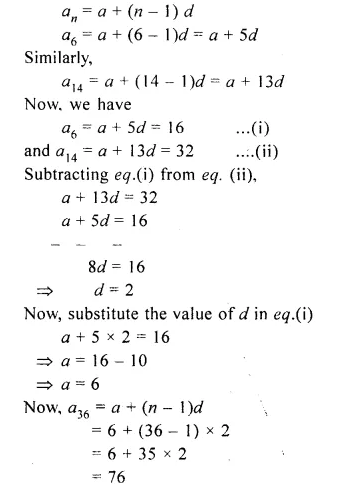
Question 2.
If the third and the 9th terms of an A.P. term is 12 and the last term is 106. Find the 29th term of the A.P.
Solution:
Let the first term and common difference of an A.P. be a and d.
As, we know that,
a_n = a + (n – 1 )d
a₃ = a + (3 – 1 )d = a + 2d
Similarly,

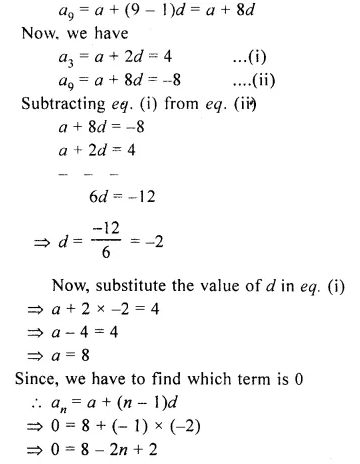
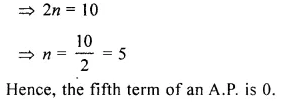
Question 3.
An A.P. consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term of the A.P.
Solution:
Number of terms in an A.P. = 50
T₃= 12, l = 106
To find T₂₉
Let a be the first term and d be the common difference
=> a + 2d = 12 …(i)

Question 4.
Find the arithmetic mean of :
(i) – 5 and 41
(ii) 3x – 2y and 3x + 2y
(iii) (m + n)² and (m – n)²
Solution:
(i) Arithmetic mean between – 5 and 41
= \(\\ \frac { -5+41 }{ 2 } \)
= \(\\ \frac { 36 }{ 2 } \)
= 18

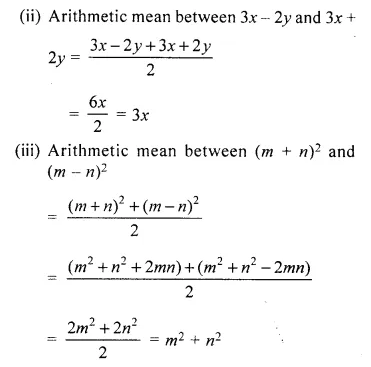
Question 5.
Find the sum of first 10 terms of the A.P. 4 + 6 + 8 +…..
Solution:
A.P. = 4 + 6 + 8 +…….
Here, a = 4, d = 6 – 4 = 2, n = 10

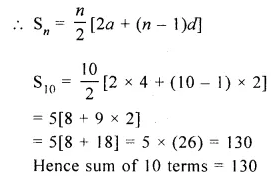
Question 6.
Find the sum of first 20 terms of an A.P. whose first term is 3 and the last term is 60.
Solution:
Sum of first 20 terms of an A.P. in which
a = 3 and a₂₀ = 60
a₂₀ = a + (20 – 1) x d
60 = 3 + 19 x d
19d = 60 – 3
d = \(\\ \frac { 57 }{ 19 } \)
= 3

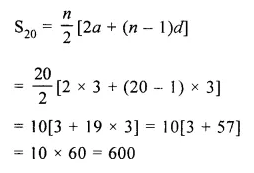
Question 7.
How many terms of the series 18 + 15 + 12 +…..when added together will give 45 ?
Solution:
A.P. is 18 + 15 + 12 +…..
Here, a = 18, d = 15 – 18 = – 3
Given : S_n = 45

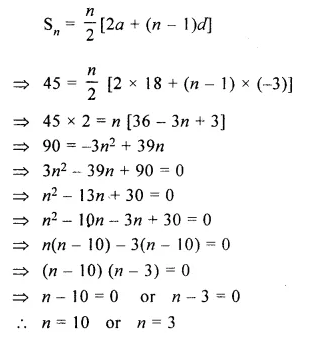
Question 8.
The nth term of a sequence is 8 – 5n. Show that the sequence is an A.P.
Solution:
Given, a_n = 8 – Sn
a₁ = 8 – 5 x (1) = 8 – 5 = 3
a₂ = 8 – 5 x (2) = 8 – 10 = – 2
a₃ = 8 – 5 x (3) = 8 – 15 = – 7
We see that

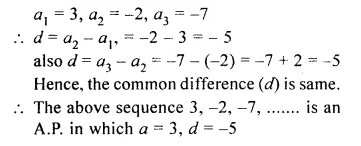
Question 9.
The the general term (nth term) and 23rd term of the sequence 3, 1, – 1, – 3,……
Solution:
The progression 3, 1, – 1, – 3,…..is A.P.
with first term (a) = 3 and common difference (d) = 1 – 3 = – 2

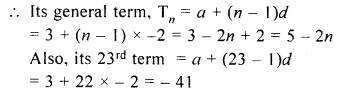
Question 10.
Which term of the sequence 3, 8, 13,…..is 78 ?
Solution:
Let 78 be the nth term
a = 3, d = 8 – 3 = 5, a_n = 78, n = ?
a + (n – 1)d = a_n

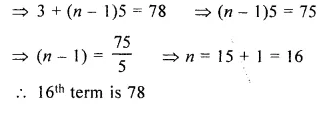
Question 11.
Is – 150 a term of 11, 8, 5, 2,….. ?
Solution:
11, 8, 5, 2,….1st term, a = 11
Common difference, d = 8 – 11 = – 3
a_n = – 150
=> a + (n – 1 )d = – 150
=> 11 + (n – 1) ( – 3) = – 150

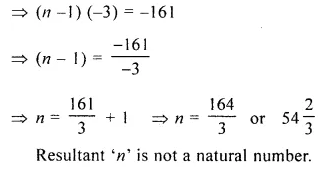
Question 12.
How many two digit numbers are divisible by 3 ?
Solution:
Numbers divisible by 3 are 3, 6, 9, 12,….
Hence, lowest two digit number divisible by 3 = 12
and highest two digit number divisible by 3 = 99

Question 13.
How many multiples of 4 lie between 10 and 250 ?
Solution:
Multiples of 4 between 10 and 250 are
12, 16, 20, 24,……, 248
Here, a = 12, d = 4, l = 248

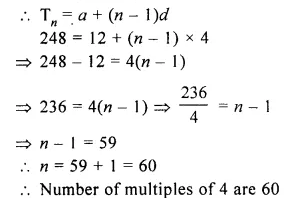
Question 14.
The sum of the 4th term and the 8th term of an A.P. is 24 and the sum of 6th term and the 10th term is 44. Find the first three terms of the A.P.
Solution:
In an A.P.
T₄ + T₈ = 24
T₆ + T₁₀ = 44
Let a be the first term and d be the common difference

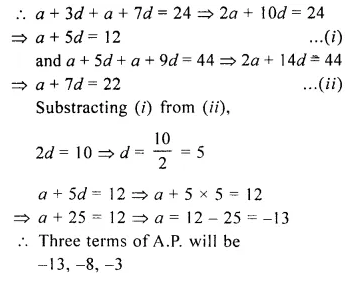
Question 15.
The sum of first 14 terms of an A.P. is 1050 and its 14th term is 140. Find the 20th term.
Solution:
Given a₁₄ = 140
we know, a_n = a + (n – 1) x d

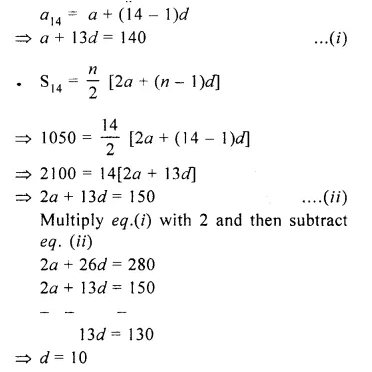
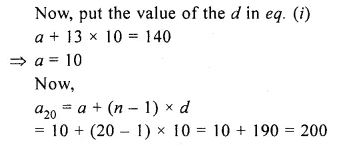
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.