Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C. https://ncertmcq.com/selina-concise-mathematics-class-10-icse-solutions/
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F
Question 1.
Find the sum of the first 22 terms of the A.P. : 8, 3, – 2,…..
Solution:
A.P. = 8, 3, – 2,…..
Here, a = 8, d = 3 – 8 = – 5, n = 22
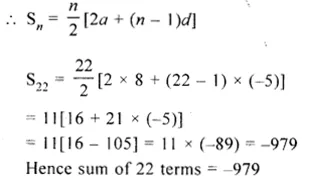
Question 2.
How many terms of the A.P. : 24, 21, 18, must be taken so that their sum is 78 ?
Solution:
Let n term of the given A.P. be taken
and A.P. = 24, 21, 18……
Let n be the number of terms.
Here, a = 24, d = 21 – 24 = – 3, Sn = 78
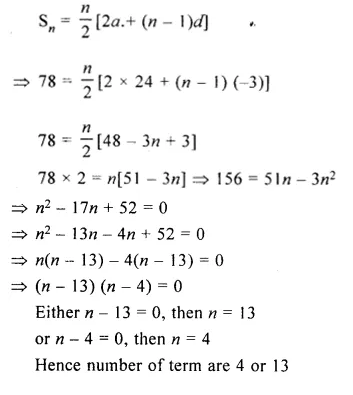
Question 3.
Find the sum of 28 terms of an A.P. whose nth term is 8n – 5.
Solution:
nth term (Tn) = 8n – 5
T1 = 8 – 5 = 3
T2 = 8 x 2 – 5 = 16 – 5 = 11
T3 = 8 x 3 – 5 = 24 – 5 = 19
A.P. is 3, 11, 19,
Here, a = 3,d = 11 – 3 = 8 and n = 28
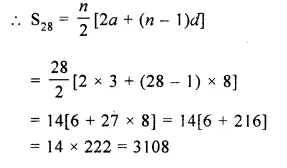
Question 4.
Find the sum of :
(i) all odd natural numbers less than 50.
(ii) first 12 natural numbers each of which is a multiple of 7.
Solution:
(i) Sum of all odd natural numbers less then 50
1 + 3 + 5 + 7 +…….+ 49
Here a = 1, d = 3 – 1 = 2
Let n be the number of term, then
49 = a + (n – 1)d
=> 49 = 1 + (n – 1) x 2
=> 49 – 1 = (n – 1) x 2
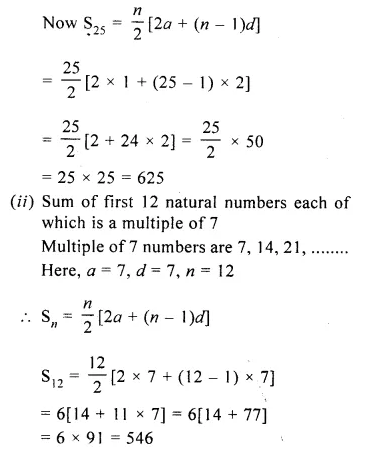
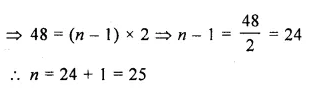
Question 5.
Find the sum of first 51 terms of an A.P. whose 2nd and 3rd terms are 14 and 18 respectively.
Solution:
Sum of first 51 terms of an A.P. in which T2 = 14 and T3 = 18
d = T3 – T2 = 18 – 14 = 4
and T2 = a + d
=> 14 = a + 4
=> a = 14 – 4 = 10
A.P. = 10, 14, 18, 22,….
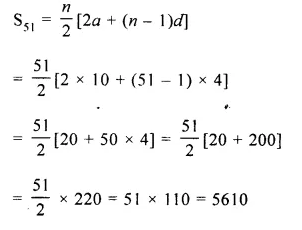
Question 6.
The sum of first 7 terms of an A.P. is 49 and that of first 17 terms of it is 289. Find the sum of first tt terms.
Solution:
S7 = 49,
S17 = 289
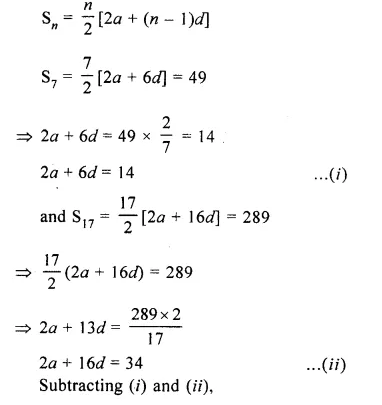
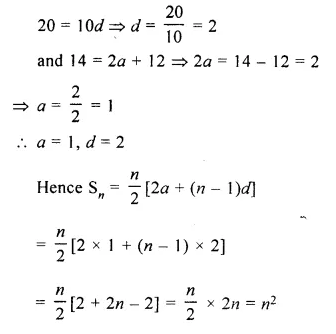
Question 7.
The first term of an A.P. is 5, the last term is 45 and the sum of its terms is 1000. Find the number of terms and the common difference of the A.P.
Solution:
First term of an AP (a) = 5
Last term = 45
and Sn = 1000

Question 8.
Find the sum of all natural numbers between 250 and 1000 which are divisible by 9.
Solution:
All natural numbers between 250 and 1000 which are divisible by 9 are
252, 261, 270……999
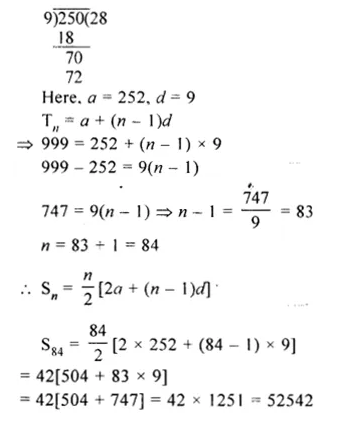
Question 9.
The first and the last terms of an A.P. are 34 and 700 respectively. If the common difference is 18, how many terms are there and what is their sum?
Solution:
In an A.P.
T1 = a = 34, l = 700, d = 18
Let n be the number of terms, then
Tn = a + (n – 1 )d
=> 700 = 34 + (n – 1) x 18
=> 700 – 34 = 18(n – 1)
=> 180 – 0 = 666

Question 10.
In an A.P. the first term is 25, nth term is – 17 and the sum of n terms is 132. Find n and the common difference.
Solution:
In an A.P.
First term (a) = 25
nth term = – 17
and Sn = 132
Let d be the common difference
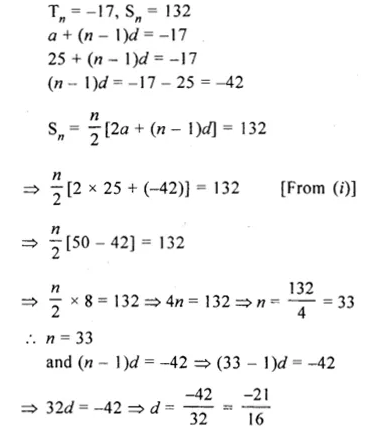
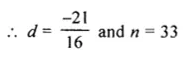
Question 11.
If the 8th term of an A.P. is 37 and the 15th term is 15 more than the 12th term, find the A.P. Also, find the sum of first 20 terms of this A.P.
Solution:
In an A.P.
8th term = 37
15th term = 12th term + 15
Let a be the first term and d be the common difference, then
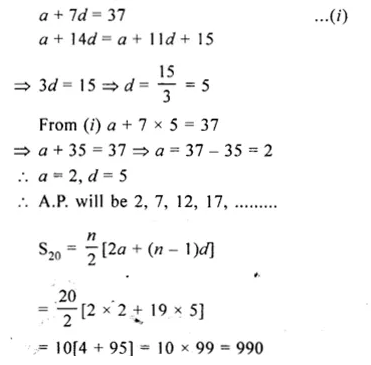
Question 12.
Find the sum of all multiples of 7 lying between 300 and 700.
Solution:
Multiples of 7 lying between 300 and 700 are 301, 308, 315, 322,…., 693
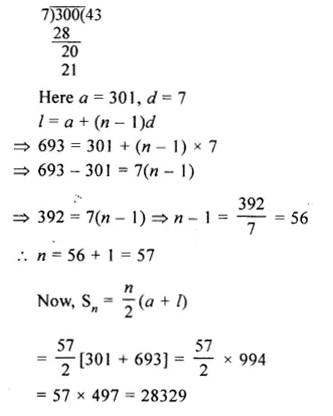
Question 13.
The sum of n natural numbers is 5n² + 4n. Find its 8th term.
Solution:
Sum of n natural number = 5n² + 4n
Sn = 5n² + 4n
S1(a) = 5 x (1)² + 4 x 1
= 5 + 4 = 9
S2 = 5(2)² + 4 x 2 = 20 + 8 = 28
S2 – S1 = T2 = 28 – 9 = 19
=> a + d = 19 => 9 + d = 19
d = 19 – 9 = 10
a = 9, d = 10
T8 = a + (n – 1 )d = 9 + (8 – 1) x 10
= 9 + 7 x 10 = 9 + 70 = 79
Question 14.
The fourth term of an A.P. is 11 and the eighth term exceeds twice the fourth term by 5. Find the A.P. and the sum of first 50 terms.
Solution:
In an A.P.
T4 = 11
T8 = 2T4 + 5
Now, a + 3d = 11
a + 7d = 2 x 11 + 5 = 22 + 5 = 27
Subtracting, 4d = 16
=> d = \(\\ \frac { 16 }{ 4 } \) = 4
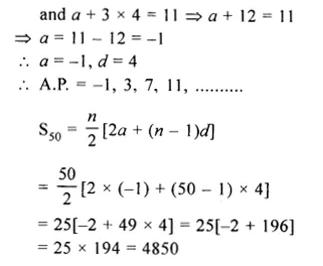
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.
