Prasanna

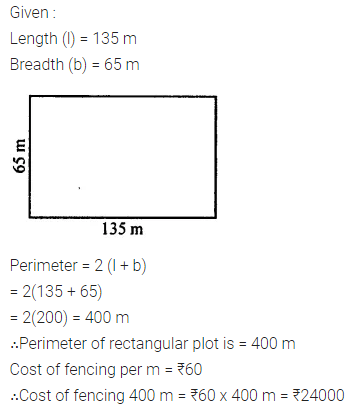
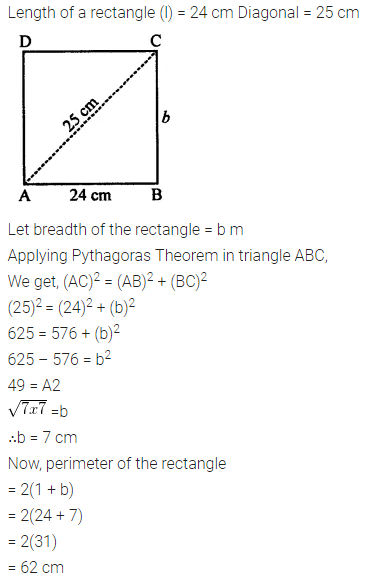
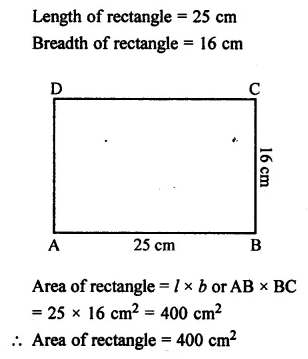
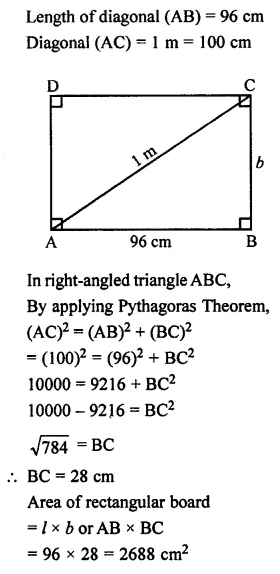
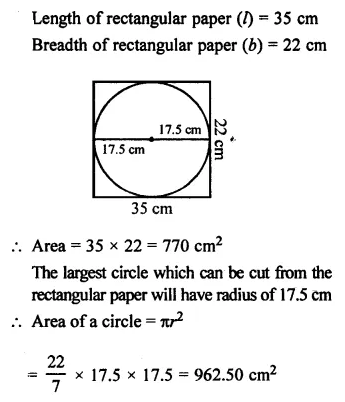
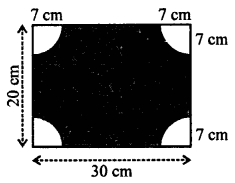
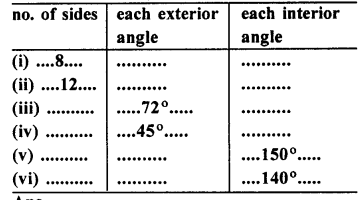
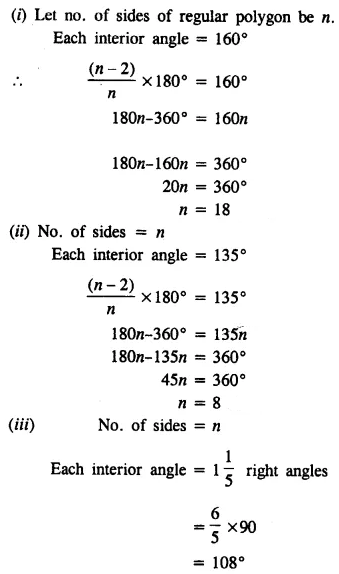
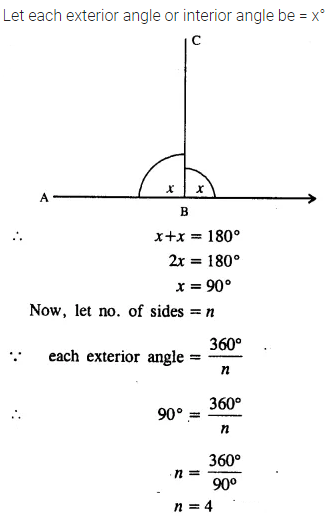
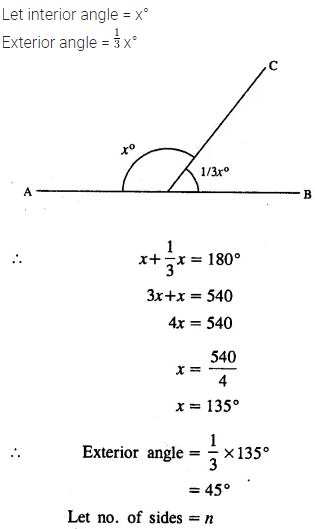
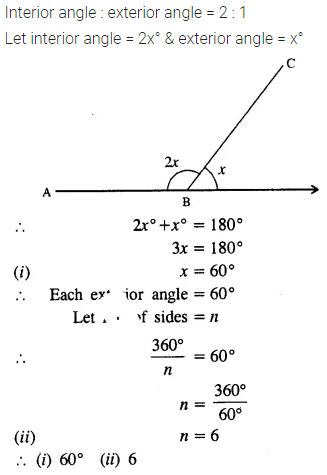
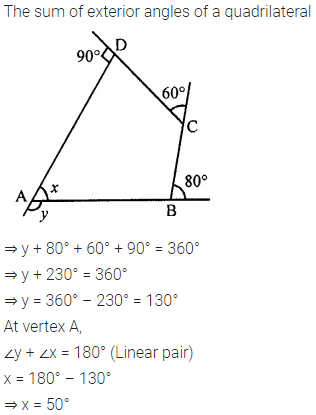
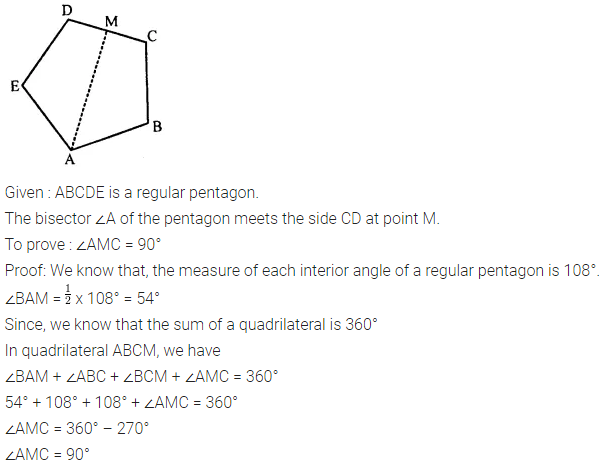
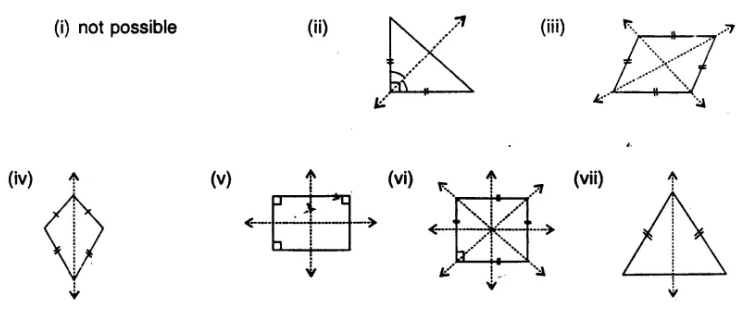
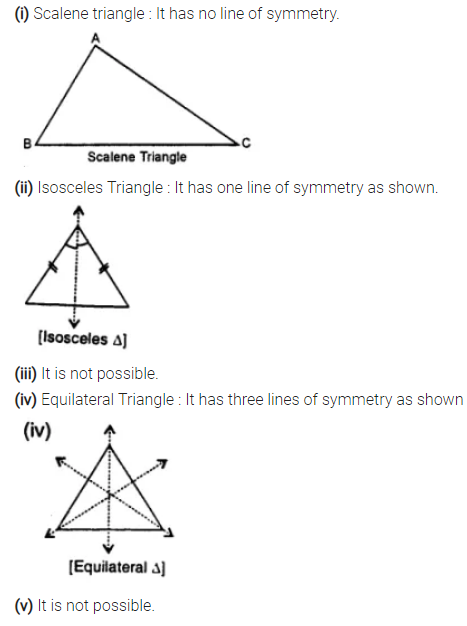
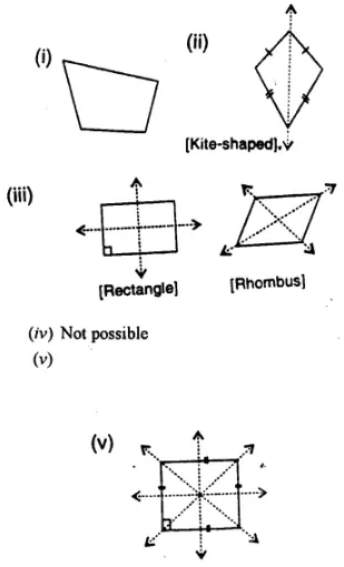
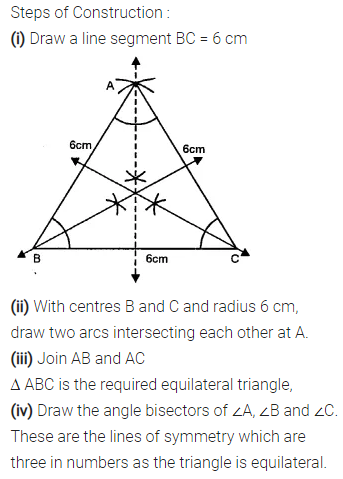
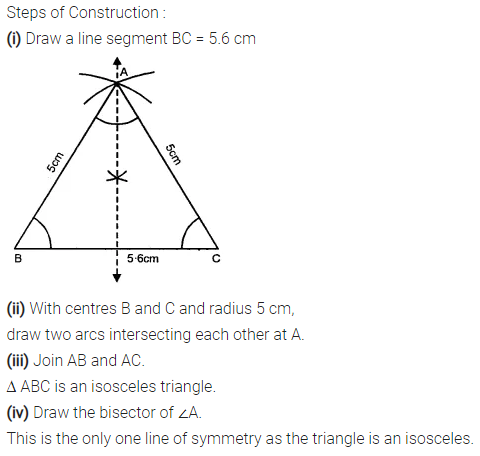
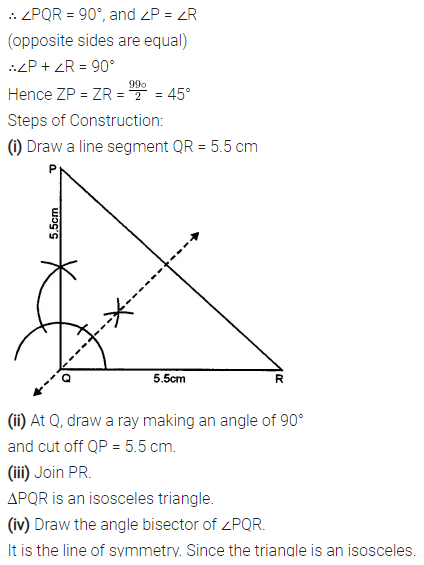
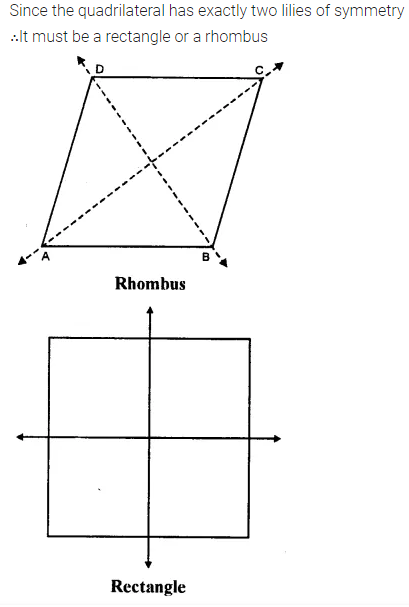
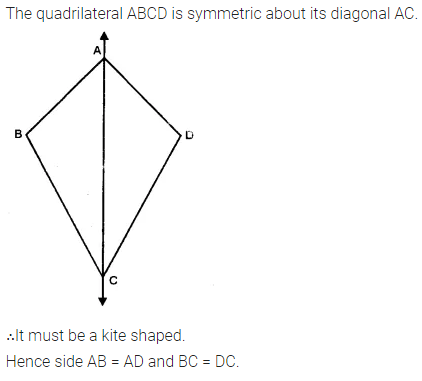
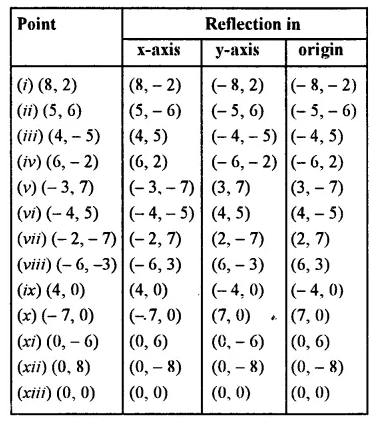
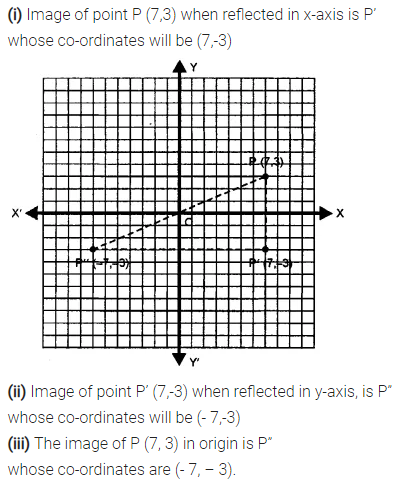
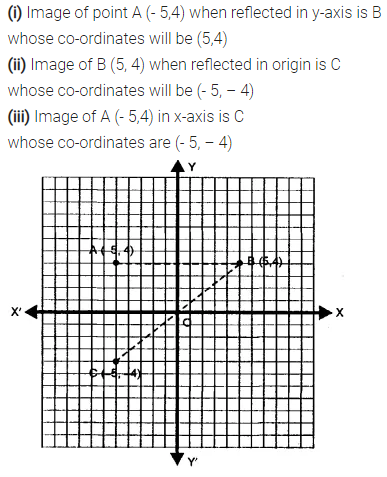
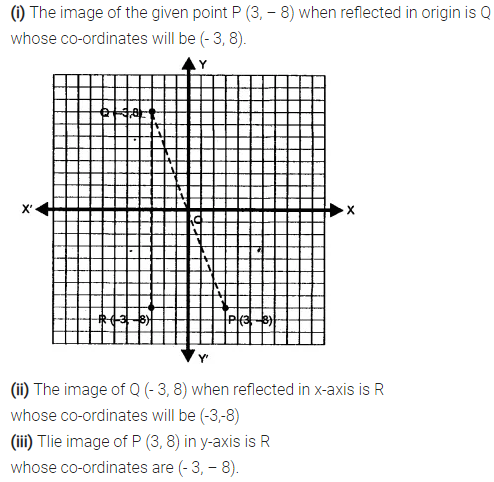
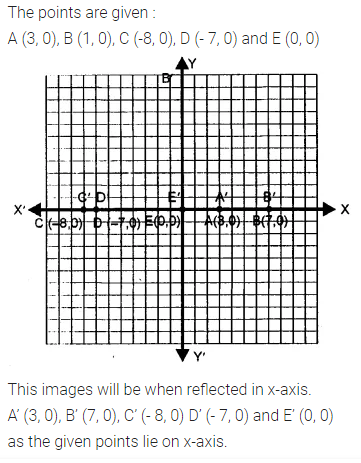
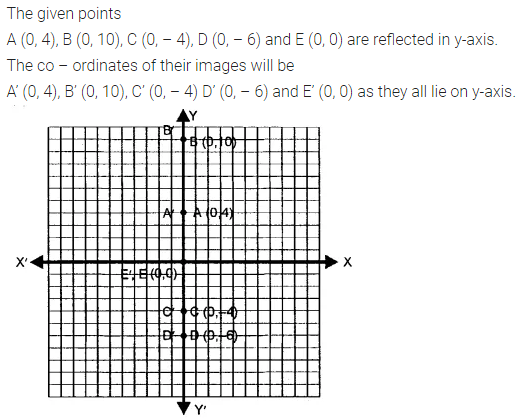
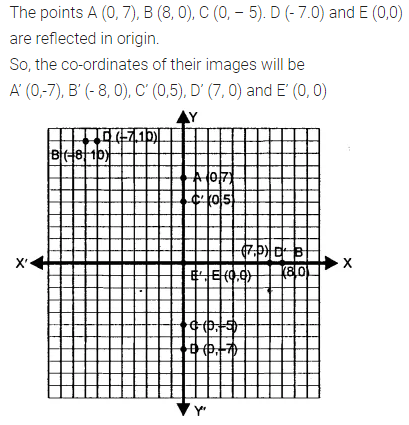
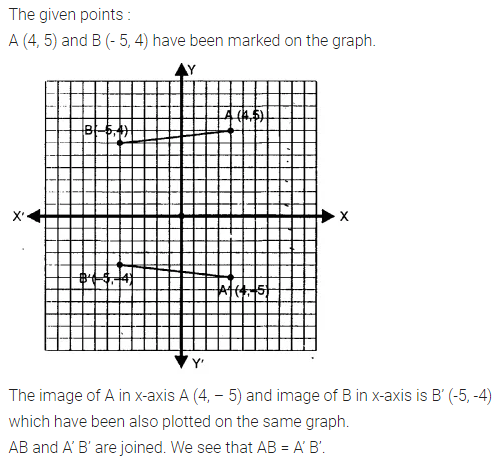
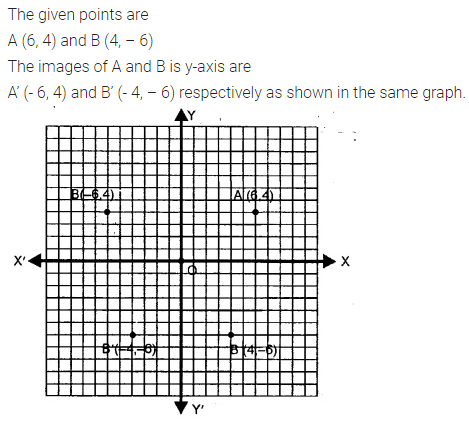
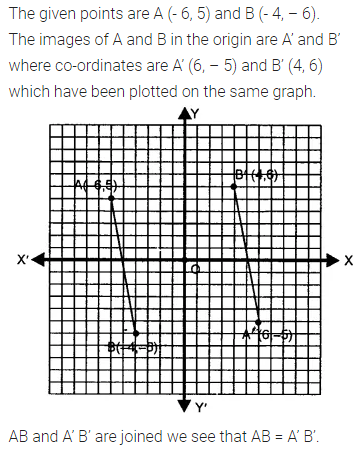
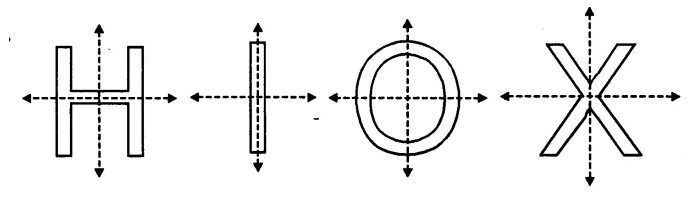
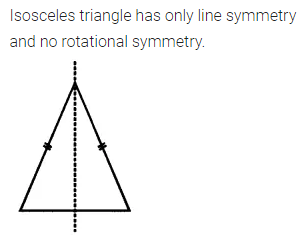
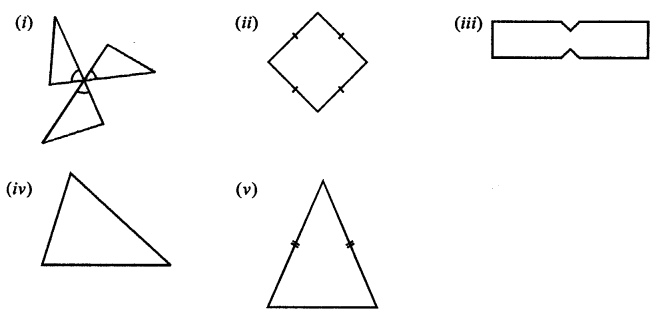
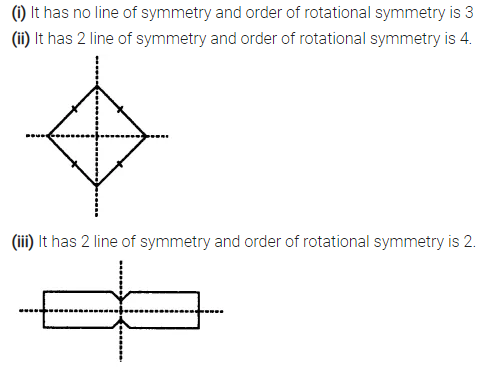
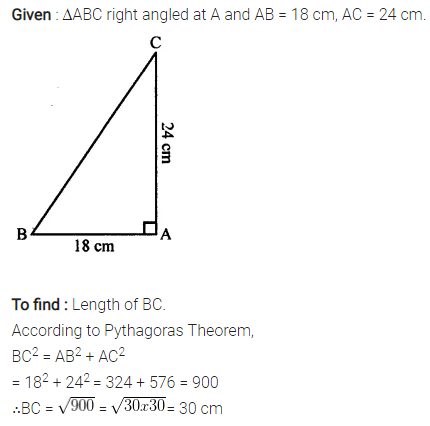
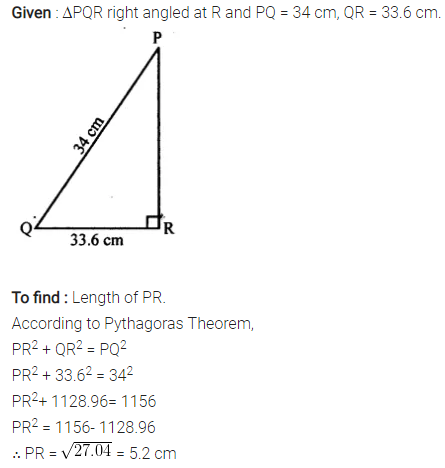
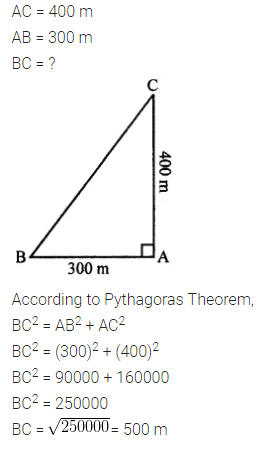
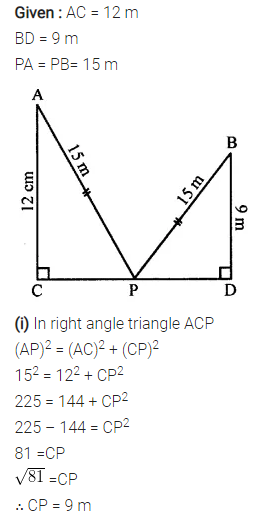
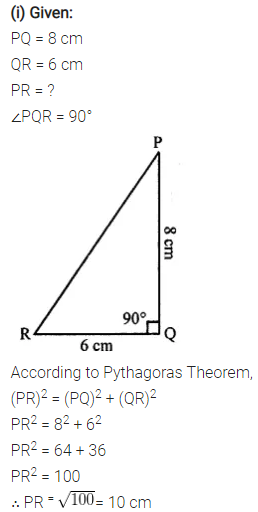
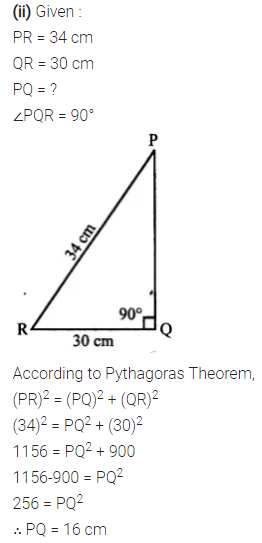
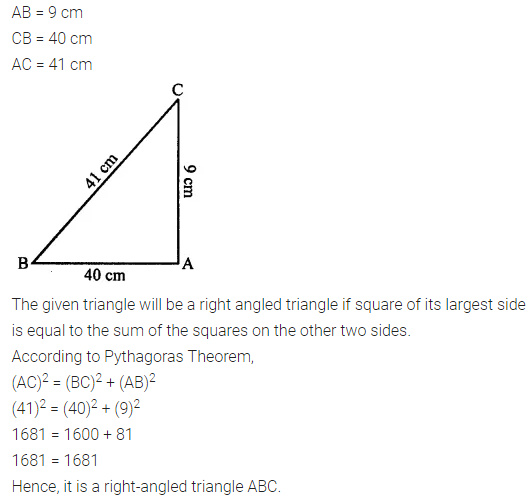
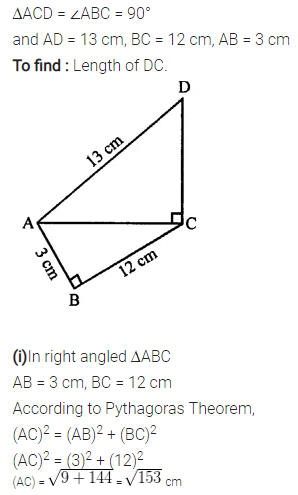
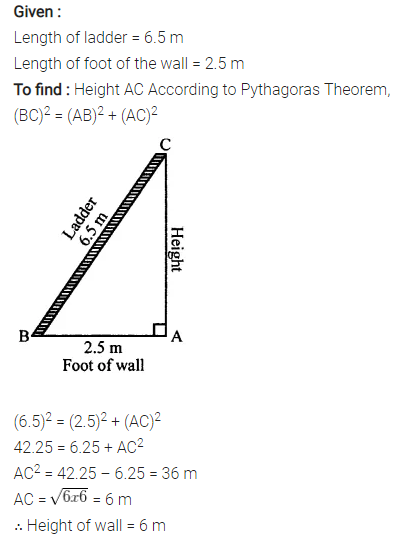
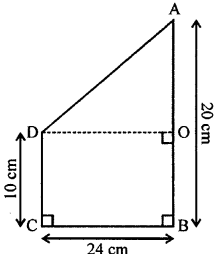
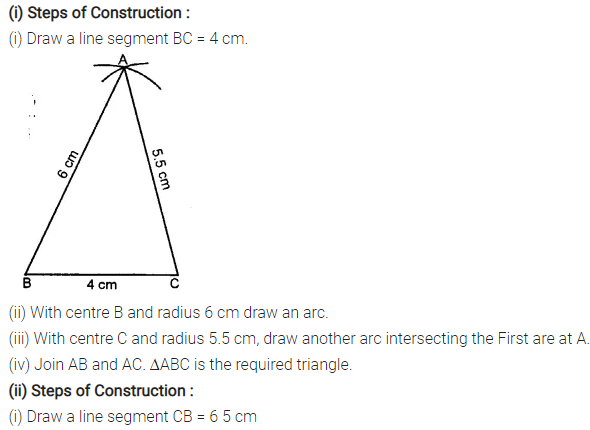
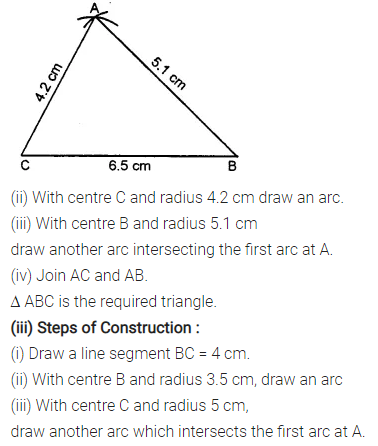
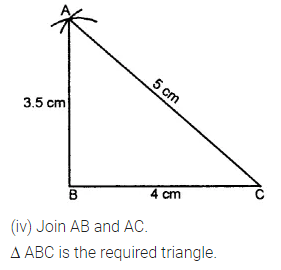
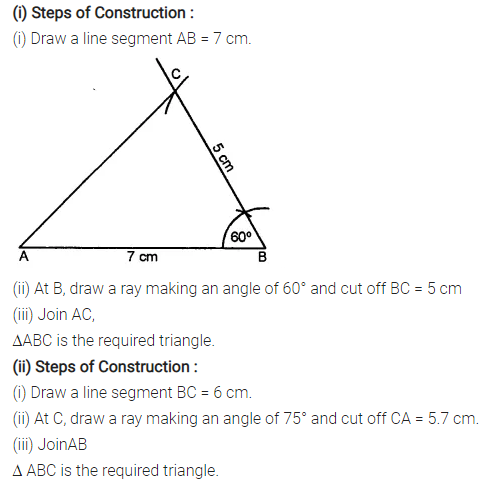
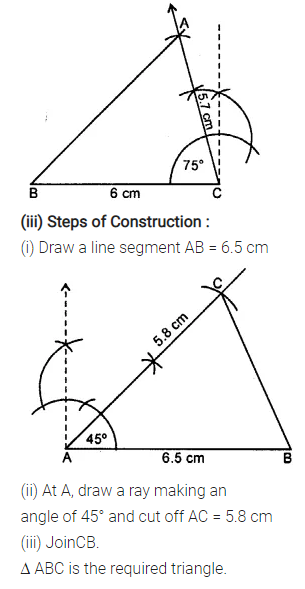
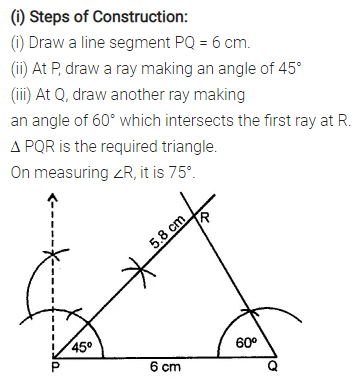
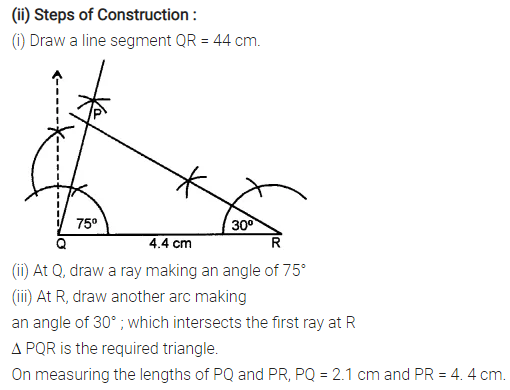
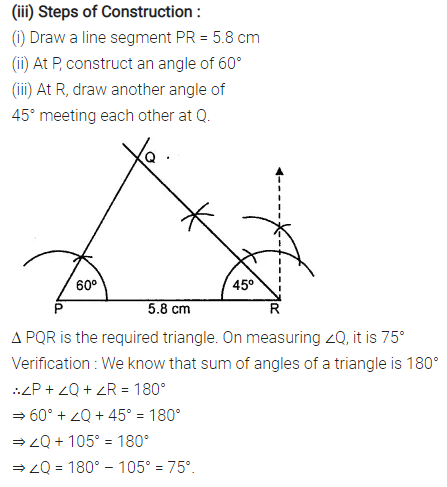
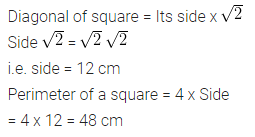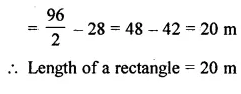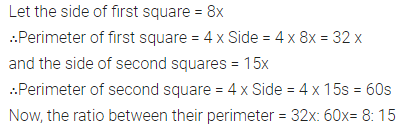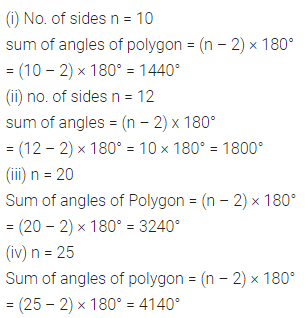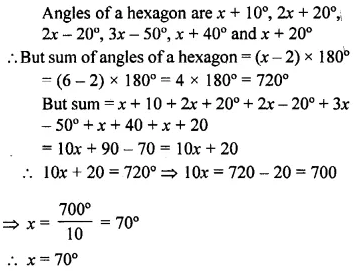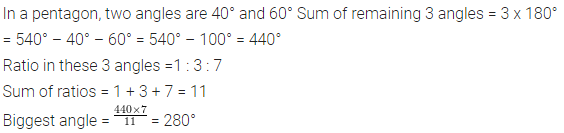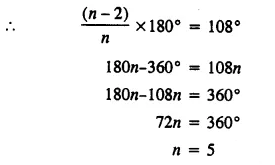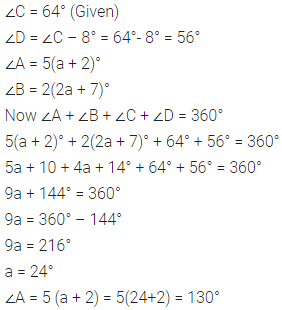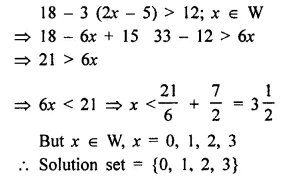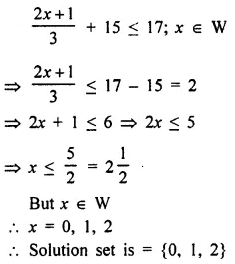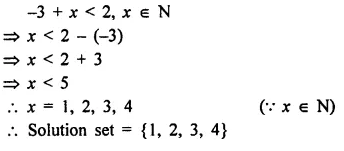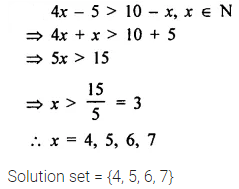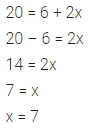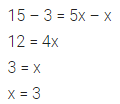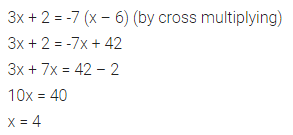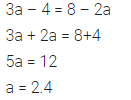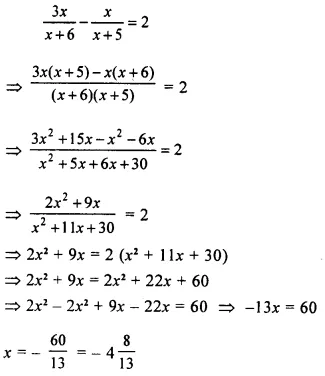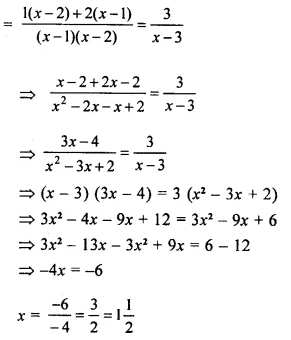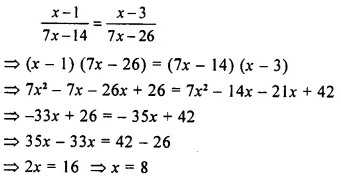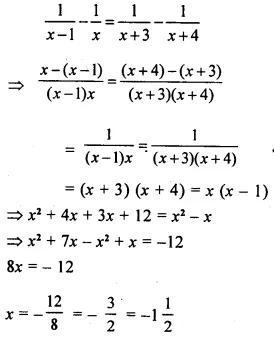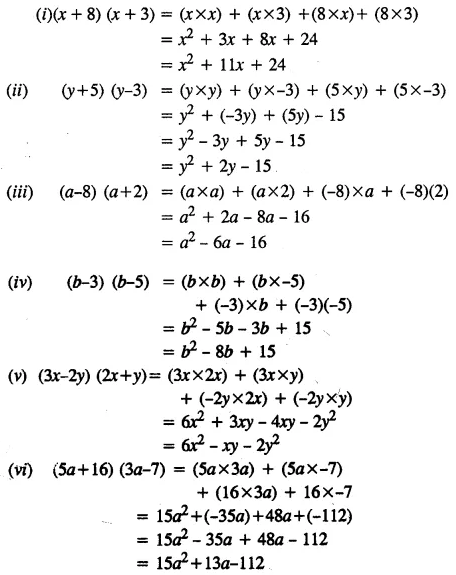Selina Concise Mathematics Class 7 ICSE Solutions Chapter 21 Data Handling

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 21 Data Handling

Data Handling Exercise 21A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Consider the following numbers :
68, 76, 63, 75, 93, 83, 70, 115, 82, 105, 90, 103, 92, 52, 99, 73, 75, 63, 77 and 71.
(i) Arrange these numbers in ascending order.
(ii) What the range of these numbers?
Solution:

Question 2.
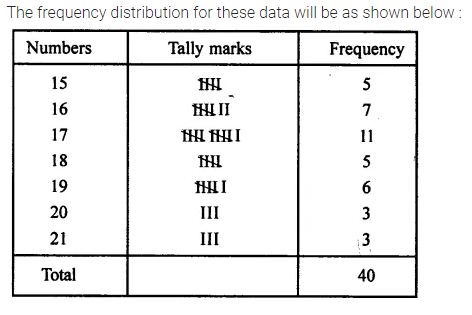
Represent the following data in the form of a frequency distribution table :
16, 17, 21, 20, 16, 20, 16, 18, 17, 21, 17, 18, 19, 17, 15, 15, 19, 19, 18, 17, 17, 15, 15, 16, 17, 17, 19, 18, 17, 16, 15, 20, 16, 17, 19, 18, 19, 16, 21 and 17.
Solution:

Question 3.
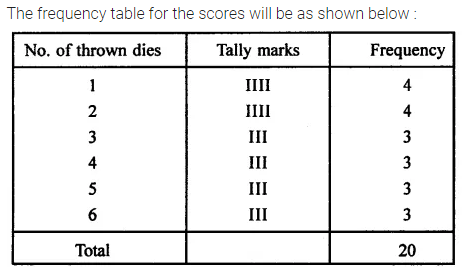
A die was thrown 20 times and following scores were recorded.
2, 1, 5, 2, 4, 3, 6, 1, 4, 2, 5, 1, 6, 2, 6, 3, 5, 4, 1 and 3.
Prepare a frequency table for the scores.
Solution:

Question 4.
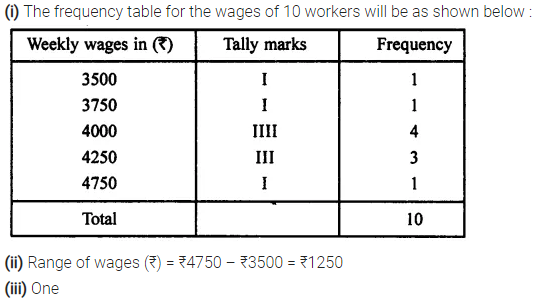
Following data shows the weekly wages (in ₹) of 10 workers in a factory.
3500, 4250, 4000, 4250, 4000, 3750, 4750, 4000, 4250 and 4000
(i) Prepare a frequency distribution table.
(ii) What is the range of wages (in ₹)?
(iii) How many workers are getting the maximum wages?
Solution:

Question 5.
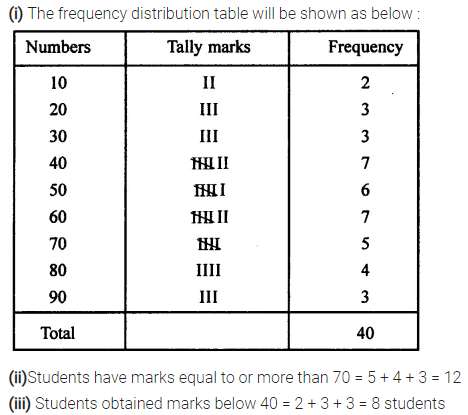
The marks obtained by 40 students of a class are given below :
80, 10, 30, 70, 60, 50, 50, 40, 40, 20, 40, 90, 50, 30, 70, 10, 60, 50, 20, 70, 70, 30, 80, 40,20, 80, 90, 50, 80, 60, 70, 40, 50, 60, 90, 60, 40, 40, 60 and 60
(i) Construct a frequency distribution table.
(ii) Find how many students have marks equal to or more than 70?
(iii) How many students obtained marks below 40?
Solution:

Question 6.
Arrange the following data in descending order:
3.3, 3.2, 3.1, 3.7, 3.6, 4.0, 3.5, 3.9, 3.8, 4.1, 3.5, 3.8, 3.7, 3.9 and 3.4.
(i) Determine the range.
(ii) How many numbers are less than 3.5?
(iii) How many numbers are 3.8 or above?
Solution:

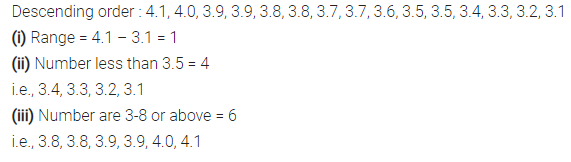
Data Handling Exercise 21B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Find the mean of 53, 61, 60, 67 and 64.
Solution:

Question 2.
Find the mean of first six natural numbers.
Solution:

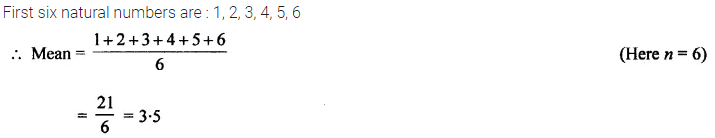
Question 3.
Find the mean of first ten odd natural numbers.
Solution:

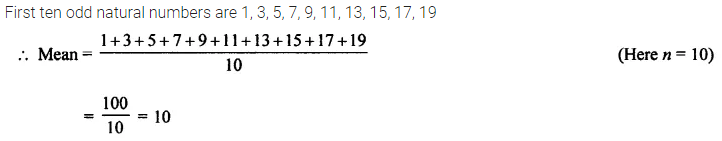
Question 4.
Find the mean of all factors of 10.
Solution:

Question 5.
Find the mean of x + 3, x + 5, x + 7, x + 9 and x + 11.
Solution:

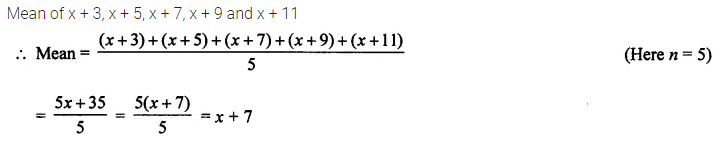
Question 6.
If different values of variable x are 19.8,15.4,13.7,11.71,11.8, 12.6,12.8,18.6,20.5 and 2.1, find the mean.
Solution:

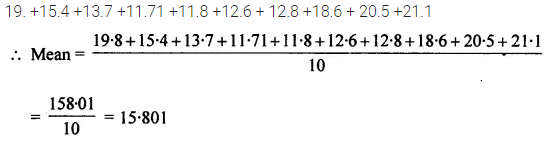
Question 7.
The mean of a certain number of observations is 32. Find the resulting mean, if each observation is,
(i) increased by 3
(ii) decreased by 7
(iii) multiplied by 2
(iv) divided by 0.5
(v) increased by 60%
(vi) decreased by 20%
Solution:

Question 8.
The pocket expenses (per day) of Anuj, during a certain week, from monday to Saturday were ₹85.40, ₹88.00, ₹86.50, ₹84.75, ₹82.60 and ₹87.25. Find the mean pocket expenses per day.
Solution:

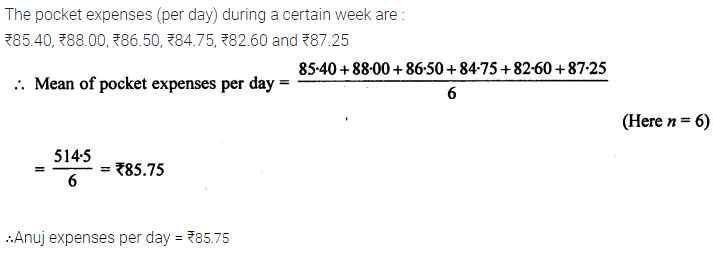
Question 9.
If the mean of 8, 10, 7, x + 2 and 6 is 9, find the value of x.
Solution:

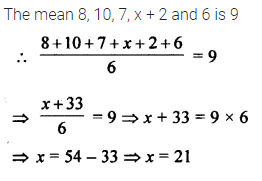
Question 10.
Find the mean of first six multiples of 3.
Solution:

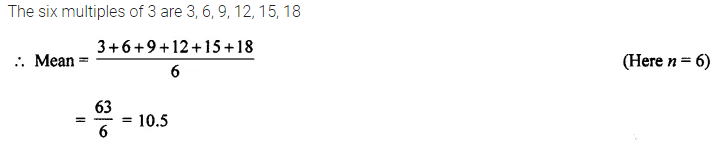
Question 11.
Find the mean of first five prime numbers.
Solution:

Question 12.
The mean of six numbers :x-5,x- 1, x, x + 2, x + 4 and x + 12 is 15. Find the mean of first four numbers.
Solution:

Question 13.
Find the mean of squares of first five whole numbers.
Solution:

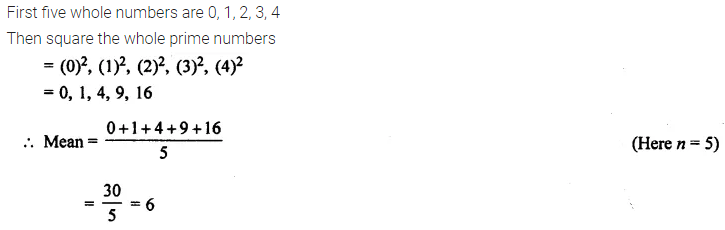
Question 14.
If the mean of 6, 4, 7, p and 10 is 8, find the value of p.
Solution:

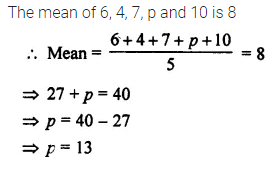
Question 15.
Find the mean of first six multiples of 5.
Solution:

Question 16.
The rainfall (in mm) in a city on 7 days of a certain week is recorded as follows

Find the total and average (mean) rainfall for the week.
Solution:

Question 17.
The mean of marks scored by 100 students was found to be 40, later on it was discovered that a score of 53 was misread as 83. Find the correct mean.
Solution:

Question 18.
The mean of five numbers is 27. If one number is excluded, the mean of remaining numbers is 25. Find the excluded number.
Solution:

Question 19.
The mean of 5 numbers is 27. If one new number is included, the new mean is 25. Find the included number.
Solution:

Question 20.
Mean of 5 numbers is 20 and mean of other 5 numbers is 30. Find the mean of all the 10 numbers taken together.
Solution:

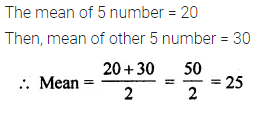
Question 21.
Find the median of:
(i) 5,7, 9, 11, 15, 17,2, 23 and 19
(ii) 9, 3, 20, 13, 0, 7 and 10
(iii) 18, 19, 20, 23, 22, 20, 17, 19, 25 and 21
(iv) 3.6, 9.4, 3.8, 5.6, 6.5, 8.9, 2.7, 10.8, 15.6, 1.9 and 7.6.
Solution:

Question 22.
Find the mean and the mode for the following data :

Solution:

Question 23.
Find the mode of:
(i) 5, 6, 9, 13, 6, 5, 6, 7, 6, 6, 3
(ii) 7, 7, 8, 10, 10, 11, 10, 13, 14
Solution:

Question 24.
Find the mode of :

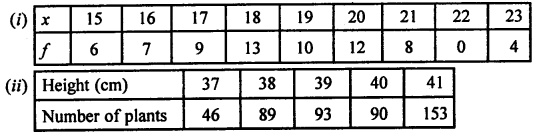
Solution:

Question 25.
The heights (in cm) of 8 girls of a class are 140,142,135,133,137,150,148 and 138 respectively. Find the mean height of these girls and their median height.
Solution:

Question 26.
Find the mean, the median and the mode of:
(i) 12, 24, 24, 12, 30 and 12
(ii) 21, 24, 21, 6, 15, 18, 21, 45, 9, 6, 27 and 15.
Solution:

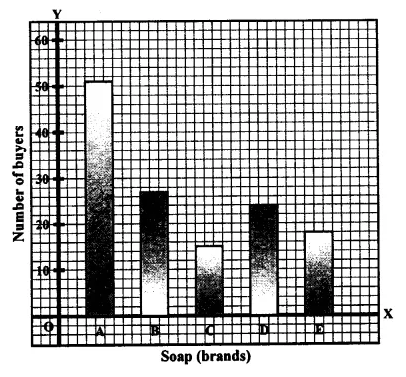
Question 27.
The following table shows the market positions of some brands of soap.
Draw a suitable bar graph :

Solution:

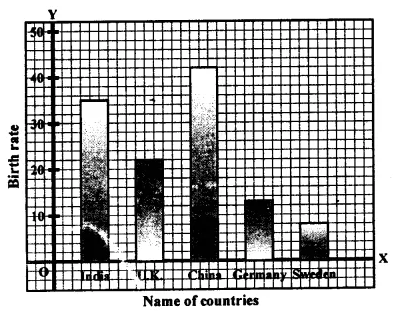
Question 28.
The birth rate per thousand of different countries over a particular period of time is shown below.

Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 20 Mensuration

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 20 Mensuration

Mensuration Exercise 20A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
The length and the breadth of a rectangular plot are 135 m and 65 m. Find, its perimeter and the cost of fencing it at the rate of ₹60 per m.
Solution:

Question 2.
The length and breadth of a rectangular field are in the ratio 7 : 4. If its perimeter is 440 m, find its length and breadth. Also, find the cost of fencing it @ ₹150 per m.
Solution:

Question 3.
The length of a rectangular field is 30 m and its diagonal is 34 m. Find the breadth of the field and its perimeter.
Solution:

Question 4.
The diagonal of a square is 12\(\sqrt { 2 } \) cm. Find its perimeter.
Solution:

Question 5.
Find the perimeter of a rectangle whose length = 22.5 m and breadth = 16 dm.
Solution:

Question 6.
Find the perimeter of a rectangle with length = 24 cm and diagonal = 25 cm
Solution:

Question 7.
The length and breadth of rectangular piece of land are in the ratio of 5 : 3. If the total cost of fencing it at the rate of ₹48 per metre is ₹19,200, find its length and breadth.
Solution:

Question 8.
A wire is in the shape of square of side 20 cm. If the wire is bent into a rectangle of length 24 cm, find its breadth.
Solution:

Question 9.
If P = perimeter of a rectangle, l= its length and b = its breadth find :
(i) P, if l = 38 cm and b = 27 cm
(ii) b, if P = 88 cm and l = 24 cm
(iii) l, if P = 96 m and b = 28 m
Solution:

Question 10.
The cost of fencing a square field at the rate of
Cost of fencing 440 m = ₹150 x 440 = ₹75 per meter is
Cost of fencing 440 m = ₹150 x 440 = ₹67,500. Find the perimeter and the side of the square field.
Solution:

Question 11.
The length and the breadth of a rectangle are 36 cm and 28 cm. If its perimeter is equal to the perimeter of a square, find the side of the square.
Solution:

Question 12.
The radius of a circle is 21 cm. Find the circumference (Take π = 3 \(\frac { 1 }{ 7 }\) ).
Solution:

Question 13.
The circumference of a circle is 440 cm. Find its radius and diameter. (Take π = \(\frac { 22 }{ 7 }\)
Solution:

Question 14.
The diameter of a circular field is 56 m. Find its circumference and cost of fencing it at the rate of ₹80 per m. (Take n = \(\frac { 22 }{ 7 }\))
Solution:

Question 15.
The radii of two circles are 20 cm and 13 cm. Find the difference between their circumferences. (Take π = \(\frac { 22 }{ 7 }\))
Solution:

Question 16.
The diameter of a circle is 42 cm, find its perimeter. If the perimeter of the circle is doubled, what will be the radius of the new circle. (Take π = \(\frac { 22 }{ 7 }\) )
Solution:

Question 17.
The perimeter of a square and the circumference of a circle are equal. If the length of each side of the square is 22 cm, find:
(i) perimeter of the square.
(ii) circumference of the circle.
(iii) radius of the circle.
Solution:

Question 18.
Find the radius of the circle whose circumference is equal to the sum of the circumferences of the circles having radii 15 cm and 8 cm.
Solution:

Question 19.
Find the diameter of a circle whose circumference is equal to the sum of circumference of circles with radii 10 cm, 12 cm and 18 cm.
Solution:

Question 20.
The circumference of a circle is eigth time the circumference of the circle with radius 12 cm. Find its diameter.
Solution:

Question 21.
The radii of two circles are in the ratio 3 : 5, find the ratio between their circumferences.
Solution:

Question 22.
The circumferences of two circles are in the ratio 5 : 7, find the ratio between their radii.
Solution:

Question 23.
The perimeters of two squares are in the ratio 8:15, find the ratio between the lengths of their sides.
Solution:

Question 24.
The lengths of the sides of two squares are in the ratio 8:15, find the ratio between their perimeters.
Solution:

Question 25.
Each side of a square is 44 cm. Find its perimeter. If this perimeter is equal to the circumference of a circle, find the radius of the circle.
Solution:

Mensuration Exercise 20B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Find the area of a rectangle whose length and breadth are 25 cm and 16 cm.
Solution:

Question 2.
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
Solution:

Question 3.
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m², find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
Solution:

Question 4.
A floor is 40 m long and 15 m broad. It is covered with tiles, each measuring 60 cm by 50 cm. Find the number of tiles required to cover the floor.
Solution:

Question 5.
The length and breadth of a rectangular piece of land are in the ratio 5 : 3. If the total cost of fencing it at the rate of ₹24 per meter is ₹9600, find its :
(i) length and breadth
(ii) area
(iii) cost of levelling at the rate of ₹60 per m².
Solution:

Question 6.
Find the area of the square whose perimeter is 56 cm.
Solution:

Question 7.
A square lawn is surrounded by a path 2.5 m wide. If the area of the path is 165 m² find the area of the lawn.
Solution:

Question 8.
For each figure, given below, find the area of shaded region : (All measurements are in cm)

Solution:

Question 9.
One side of a parallelogram is 20 cm and its distance from the opposite side is 16 cm. Find the area of the parallelogram.
Solution:

Question 10.
The base of a parallelogram is thrice it height. If its area is 768 cm², find the base and the height of the parallelogram.
Solution:

Question 11.
Find the area of the rhombus, if its diagonals are 30 cm and 24 cm.
Solution:

Question 12.
If the area of a rhombus is 112 cm² and one of its diagonals is 14 cm, find its other diagonal.
Solution:

Question 13.
One side of a parallelogram is 18 cm and its area is 153 cm². Find the distance of the given side from its opposite side.
Solution:

Question 14.
The adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between the longer sides is 6 cm, find the distance between the shorter sides.
Solution:

Question 15.
The area of a rhombus is 84 cm2 and its perimeter is 56 cm. Find its height.
Solution:

Question 16.
Find the area of a triangle whose base is 30 cm and height is 18 cm.
Solution:

Question 17.
Find the height of a triangle whose base is 18 cm and area is 270 cm².
Solution:

Question 18.
The area of a right-angled triangle is 160 cm². If its one leg is 16 cm long, find the length of the other leg.
Solution:

Question 19.
Find the area of a right-angled triangle whose hypotenuse is 13 cm long and one of its legs is 12 cm long.
Solution:

Question 20.
Find the area of an equilateral triangle whose each side is 16 cm. (Take \(\sqrt { 3 } \)= 1.73)
Solution:

Question 21.
The sides of a triangle are 21 cm, 17 cm and 10 cm. Find its area.
Solution:

Question 22.
Find the area of an isosceles triangle whose base is 16 cm and length of each of the equal sides is 10 cm.
Solution:

Question 23.
Find the base of a triangle whose area is 360 cm²and height is 24 cm.
Solution:

Question 24.
The legs of a right-angled triangle are in the ratio 4 :3 and its area is 4056 cm². Find the length of its legs.
Solution:

Question 25.
The area of an equilateral triangle is (64 x \(\sqrt { 3 } \) ) cm²– Find the length of each side of the triangle.
Solution:

Question 26.
The sides of a triangle are in the ratio 15 : 13 : 14 and its perimeter is 168 cm. Find the area of the triangle.
Solution:

Question 27.
The diameter of a circle is 20 cm. Taking π = 3.14, find the circumference and its area.
Solution:

Question 28.
The circumference of a circle exceeds its diameter by 18 cm. Find the radius of the circle.
Solution:

Question 29.
The ratio between the radii of two circles is 5 : 7. Find the ratio between their :
(i) circumference
(ii) areas
Solution:

Question 30.
The ratio between the areas of two circles is 16 : 9. Find the ratio between their :
(i) radii
(ii) diameters
(iii) circumference
Solution:

Question 31.
A circular racing track has inner circumference 528 m and outer circumference 616 m. Find the width of the track.
Solution:

Question 32.
The inner circumference of a circular track is 264 m and the width of the track is 7 m. Find:
(i) the radius of the inner track.
(ii) the radius of the outer circumference.
(iii) the length of the outer circumference.
(iv) the cost of fencing the outer circumference at the rate of ₹50 per m.
Solution:

Question 33.
The diameter of every wheel of a car is 63 cm. How much distance will the car move during 2000 revolutions of its wheel.
Solution:

Question 34.
The diameter of the wheel of a car is 70 cm. How many revolutions will it make to travel one kilometre?
Solution:

Question 35.
A metal wire, when bent in the form of a square of largest area, encloses an area of 484 cm². Find the length of the wire. If the same wire is bent to a largest circle, find:
(i) radius of the circle formed.
(ii) area of the circle.
Solution:

Question 36.
A wire is along the boundary of a circle with radius 28 cm. If the same wire is bent in the form of a square, find the area of the square formed.
Solution:

Question 37.
The length and the breadth of a rectangular paper are 35 cm and 22 cm. Find the area of the largest circle which can be cut out of this paper.
Solution:

Question 38.
From each comer of a rectangular paper (30 cm x 20 cm) a quadrant of a circle of radius 7 cm is cut. Find the area of the remaining paper i.e., shaded portion.

Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 16 Understanding Shapes (Including Polygons)

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 16 Understanding Shapes (Including Polygons)

Understanding Shapes Exercise 16A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
State which of the following are polygons :

If the given figure is a polygon, name it as convex or concave.
Solution:

Question 2.
Calculate the sum of angles of a polygon with :
(i) 10 sides
(ii) 12 sides
(iii) 20 sides
(iv) 25 sides
Solution:

Question 3.
Find the number of sides in a polygon if the sum of its interior angles is :
(i) 900°
(ii) 1620°
(iii) 16 right-angles
(iv) 32 right-angles.
Solution:

Question 4.
Is it possible to have a polygon ; whose sum of interior angles is :
(i) 870°
(ii) 2340°
(iii) 7 right-angles
(iv) 4500°
Solution:

Question 5.
(i) If all the angles of a hexagon are equal ; find the measure of each angle.
(ii) If all the angles of a 14-sided figure are equal ; find the measure of each angle.
Solution:

Question 6.
Find the sum of exterior angles obtained on producing, in order, the sides of a polygon with :
(i) 7 sides
(ii) 10 sides
(iii) 250 sides.
Solution:

Question 7.
The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are (6x – 1)°, (10x + 2)°, (8x + 2)° (9x – 3)°, (5x + 4)° and (12x + 6)° ; find each exterior angle.
Solution:

Question 8.
The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.
Solution:

Question 9.
Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.
Solution:

Question 10.
The figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5 : 6 : 7.

(i) Using formula, find the sum of interior angles of the pentagon.
(ii) Write the value of ∠A + ∠E
(iii) Find angles B, C and D.
Solution:

Question 11.
Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
Solution:

Question 12.
In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.
Solution:

Question 13.
the angles of a hexagon are x + 10°, 2x + 20°, 2x – 20°, 3x – 50°, x + 40° and x + 20°. Find x.
Solution:

Question 14.
In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.
Solution:

Understanding Shapes Exercise 16B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Fill in the blanks :
In case of regular polygon, with :

Solution:

Question 2.
Find the number of sides in a regular polygon, if its each interior angle is :
(i) 160°
(ii) 135°
(iii) \(1\frac { 1 }{ 5 }\) of a right-angle
Solution:

Question 3.
Find the number of sides in a regular polygon, if its each exterior angle is :
(i) \(\frac { 1 }{ 3 }\) of a right angle
(ii) two-fifth of a right-angle.
Solution:

Question 4.
Is it possible to have a regular polygon whose each interior angle is :
(i) 170°
(ii) 138°
Solution:

Question 5.
Is it possible to have a regular polygon whose each exterior angle is :
(i) 80°
(ii) 40% of a right angle.
Solution:
</span

Question 6.
Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
Solution:

Question 7.
The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
Solution:

Question 8.
The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
Solution:

Question 9.
The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find :
(i) each exterior angle of the polygon ;
(ii) number of sides in the polygon
Solution:

Question 10.
The ratio between the exterior angle and the interior angle of a regular polygon is 1 : 4. Find the number of sides in the polygon.
Solution:

Question 11.
The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
Solution:

Question 12.
AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20° ; find :
(i) its each interior angle,
(ii) its each exterior angle
(iii) the number of sides in the polygon.
Solution:

Question 13.
Two alternate sides of a regular polygon, when produced, meet at the right angle. Calculate the number of sides in the polygon.
Solution:

Question 14.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Solution:

Question 15.
The difference between the exterior angles of two regular polygons, having the sides equal to (n – 1) and (n + 1) is 9°. Find the value of n.
Solution:

Question 16.
If the difference between the exterior angle of a n sided regular polygon and an (n + 1) sided regular polygon is 12°, find the value of n.
Solution:

Question 17.
The ratio between the number of sides of two regular polygons is 3 : 4 and the ratio between the sum of their interior angles is 2 : 3. Find the number of sides in each polygon.
Solution:

Question 18.
Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. If each of the remaining exterior angles is x°, find the value of x.
Solution:

Question 19.
Calculate the number of sides of a regular polygon, if:
(i) its interior angle is five times its exterior angle.
(ii) the ratio between its exterior angle and interior angle is 2 : 7.
(iii) its exterior angle exceeds its interior angle by 60°.
Solution:

Question 20.
The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Solution:

Understanding Shapes Exercise 16C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Solution:

Question 2.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Solution:

Question 3.
Angles of a quadrilateral are (4x)°, 5(x + 2)°, (7x – 20)° and 6(x + 3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Solution:

Question 4.
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C

Solution:

Question 5.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
Solution:

Question 6.
From the following figure find ;
(i) x
(ii) ∠ABC
(iii) ∠ACD
Solution:

Question 7.
Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a + 2)° and ∠B = 2(2a + 7)°.
Calculate ∠A.
Solution:

Question 8.
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.

Solution:

Question 9.
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
Solution:

Question 10.
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
Solution:

Question 11.
Use the informations given in the following figure to find the value of x.

Solution:

Question 12.
The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.

Solution:

Question 13.
Use the following figure to find the value of x

Solution:

Question 14.
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Solution:

Question 15.
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = \(\frac { 1 }{ 2 }\) (∠C + ∠D)
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 18 Recognition of Solids (Representing 3-D in 2-D)

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 18 Recognition of Solids (Representing 3-D in 2-D)

Recognition of solids Exercise 18 – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Identify the nets which can be used to form cubes

Solution:

Question 2.
Draw at least three different nets for making cube.
Solution:

Question 3.
The figure, given below, shows shadows of some 3D objects, when seen under the lamp of an overhead projector :

In each case, name the object.
Solution:

Question 4.
Using Euler’s formula, find the values of a, b, c and d.

Solution:

Question 5.
Dice are cubes with dot or dots on each face. Opposite faces of a die always have a total of seven on them.
Below are given two nets to make dice (cube), the numbers inserted in each square indicate the number of dots in it.

Insert suitable numbers in each blank so that numbers in opposite faces of the die have a total of seven dots.
Solution:

Question 6.
The following figures represent nets of some solids. Name the solids

Solution:

Question 7.
Draw a map of your class room using proper scale and symbols for different objects.
Solution:

Question 8.
Draw a map of your school compound using proper scale and symbols for various features like play ground, main building, garden, etc.
Solution:

Question 9.
In the map of India, the distance between two cities is 13.8 cm.
Taking scale : 1 cm = 12 km, find the actual distance between these two cities.
Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 15 Linear Inequations (Including Number Lines)

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 15 Linear Inequations (Including Number Lines)

Linear Inequations Exercise 15A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
If the replacement set is the set of natural numbers, solve.
(i) x – 5 < 0
(ii) x + 1 < 7
(iii) 3x – 4 > 6
(iv) 4x + 1 > 17
Solution:

Question 2.
If the replacement set = {-6, -3, 0, 3, 6, 9}; find the truth set of the following:
(i) 2x – 1 > 9
(ii) 3x + 7 < 1
Solution:

Question 3.
Solve 7 > 3x – 8; x ∈ N
Solution:

Question 4.
-17 < 9y – 8 ; y ∈ Z
Solution:

Question 5.
Solve 9x – 7 ≤ 28 + 4x; x ∈ W
Solution:

Question 6.
Solve : \(\frac { 2 }{ 3 }\)x + 8 < 12 ; x ∈ W
Solution:

Question 7.
Solve -5 (x + 4) > 30 ; x ∈ Z
Solution:

Question 8.
Solve the inquation 8 – 2x > x – 5 ; x ∈ N.
Solution:

Question 9.
Solve the inequality 18 – 3 (2x – 5) > 12; x ∈ W.
Solution:

Question 10.
Solve : \(\frac { 2x+1 }{ 3 }\) + 15 < 17; x ∈ W.
Solution:

Question 11.
Solve : -3 + x < 2, x ∈ N
Solution:

Question 12.
Solve : 4x – 5 > 10 – x, x ∈ {0, 1, 2, 3, 4, 5, 6, 7}
Solution:

Question 13.
Solve : 15 – 2(2x – 1) < 15, x ∈ Z.
Solution:

Question 14.
Solve : \(\frac { 2x+3 }{ 5 }\) > \(\frac { 4x-1 }{ 2 }\) , x ∈ W.
Solution:

Linear Inequations Exercise 15B – Selina Concise Mathematics Class 8 ICSE Solutions

Solve and graph the solution set on a number line :
Question 1.
x – 5 < -2 ; x ∈ N
Solution:

Question 2.
3x – 1 > 5 ; x ∈ W
Solution:

Question 3.
-3x + 12 < -15 ; x ∈ R.
Solution:

Question 4.
7 > 3x – 8 ; x ∈ W
Solution:

Question 5.
8x – 8 < – 24 ; x ∈ Z
Solution:

Question 6.
8x – 9 > 35 – 3x ; x ∈ N
Solution:

Question 7.
5x + 4 > 8x – 11 ; x ∈ Z
Solution:

Question 8.
\(\frac { 2x }{ 5 }\) + 1 < -3 ; x ∈ R
Solution:

Question 9.
\(\frac { x }{ 2 }\) > -1 + \(\frac { 3x }{ 4 }\) ; x ∈ N
Solution:

Question 10.
\(\frac { 2 }{ 3 }\) x + 5 ≤ \(\frac { 1 }{ 2 }\) x + 6 ; x ∈ W
Solution:

Question 11.
Solve the inequation 5(x – 2) > 4 (x + 3) – 24 and represent its solution on a number line.
Given the replacement set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Solution:

Question 12.
Solve \(\frac { 2 }{ 3 }\) (x – 1) + 4 < 10 and represent its solution on a number line.
Given replacement set is {-8, -6, -4, 3, 6, 8, 12}.
Solution:

Question 13.
For each inequation, given below, represent the solution on a number line :
(i) \(\frac { 5 }{ 2 }\) – 2x ≥ \(\frac { 1 }{ 2 }\) ; x ∈ W
(ii) 3(2x – 1) ≥ 2(2x + 3), x ∈ Z
(iii) 2(4 – 3x) ≤ 4(x – 5), x ∈ W
(iv) 4(3x + 1) > 2(4x – 1), x is a negative integer
(v) \(\frac { 4 – x }{ 2 }\) < 3, x ∈ R
(vi) -2(x + 8) ≤ 8, x ∈ R
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 17 Symmetry (Including Reflection and Rotation)

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 17 Symmetry (Including Reflection and Rotation)

Symmetry Exercise 17A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
For each figure, given below, draw the line (s) of symmetry, if possible :

Solution:

Question 2.
Write capital letters A to Z of English alphabet ; and in each case, if possible, draw the largest number of lines of symmetry.
Solution:

Question 3.
By drawing a free hand sketch of each of the following, draw in each case, the line (s) of symmetry,
if any:
(i) a scalene triangle
(ii) an isosceles right angled triangle
(iii) a rhombus
(iv) a kite shaped figure triangle.
(v) a rectangle
(vi) a square
(vii) an isosceles
Solution:

Question 4.
Draw a triangle with :
(i) no line of symmetry,
(ii) only one line of symmetry,
(iii) exactly two lines of symmetry,
(iv) exactly three lines of symmetry,
(v) more than three lines of symmetry.
In each case, if possible, represent the line/ lines of symmetry by dotted lines. Also, write the special name of the triangle drawn.
Solution:

Question 5.
Draw a quadrilateral with :
(i) no line of symmetry.
(ii) only one line of symmetry.
(iii) exactly two lines of symmetry.
(iv) exactly three lines of symmetry.
(v) exactly four lines of symmetry.
(vi) more than four lines of symmetry.
In each case, if possible, represent the line/ lines of symmetry by dotted lines. Also, write the special name of the quadrilateral drawn.
Solution:

Question 6.
Construct an equilateral triangle with each side 6 cm. In the triangle drawn, draw all the possible lines of symmetry.
Solution:

Question 7.
Construct a triangle ABC in which AB = AC = 5cin and BC = 5.6 cm. If possible, draw its lines of symmetry.
Solution:

Question 8.
Construct a triangle PQR such that PQ = QR = 5 .5 cm and angle PQR = 90°. If possible, draw its lines of symmetry.
Solution:

Question 9.
If possible, draw a rough sketch of a quadrilateral which has exactly two lines of symmetry.
Solution:

Question 10.
A quadrilateral ABCD is symmetric about its diagonal AC. Name tire sides of this quadrilateral which are equal.
Solution:

Symmetry Exercise 17B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
In each figure, given below, find the image of the point P in the line AB :

Solution:

Question 2.
In each figure, given below, find the image of the line segment AB in the line PQ :

Solution:

Question 3.
Complete the following table :

Solution:

Question 4.
A point P (7,3)|is reflected in x-axis to point P’. The point P’ is further reflected in v-axis to point P” Find :
(i) the co-ordinates of P’
(ii) the co-ordinates of P”
(iii) the image of P (7, 3) in origin.
Solution:

Question 5.
A point A (- 5, 4) is reflected in y-axis to point B. The point B is further reflected in origin to point C. find :
(i) the co-ordinates of B
(ii) the co-ordinates of C
(iii) the image of A (- 5, 4) in x-axis.
Solution:

Question 6.
The point P (3, – 8) is reflected in origin to point Q. The Point Q is further reflected in x-axis to point R. Find :
(i) the co-ordinates of Q
(ii) the co-ordinates of R
(iii) the image of P (3, – 8) in y-axis.
Solution:

Question 7.
Each of the points A (3, 0), B (7, 0), C (- 8, 0), D (- 7, 0) and E (0, 0) is reflected in x-axis to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Solution:

Question 8.
Each of the points A (0, 4), B (0, 10), C (0, – 4), D (0, – 6) and E (0, 0) is reflected in y-axis to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Solution:

Question 9.
Each of the points A (0, 7), B (8. 0), C (0, -5), D (- 7, 0) and E (0, 0) are reflected in origin to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Solution:

Question 10.
Mark points A (4, 5) and B (- 5, 4) on a graph paper. Find A’, the image of A in x-axis and B’, the image of B in x-axis.
Mark A’ and B’ also on the same graph paper.
(ii) Join AB and A’ B’ and
find if AB = A’ B’ ?
Solution:

Question 11.
Mark points A (6, 4) and B (4, – 6) on a graph paper.
Find A’, the image of A in y-axis and B’, the image of B in y-axis. Mark A’ and B’ also on the same graph paper.
Solution:

Question 12.
Mark points A (- 6, 5) and B (- 4, – 6) on a graph paper. Find A’, the image of A in origin and B’, the image of B in origin. Mark A’ and B’ also on the same graph paper. Join AB and A’ B’. Is AB = A’ B’ ?
Solution:

Symmetry Exercise 17C – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
How many lines of symmetry does a rhombus have?
Solution:

Question 2.
What is the order of rotational symmetry of a rhombus?
Solution:

Question 3.
Show that each of the following figures has two lines of symmetry and a rotational.

Solution:

Question 4.
Name a figure that has a line of symmetry but does not have any roational symmetry.
Solution:

Question 5.
In each of the following figures, draw all possible lines of symmetry and also write the order of rotational symmetry:

Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 14 Linear Equations in one Variable (With Problems Based on Linear equations)

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 14 Linear Equations in one Variable (With Problems Based on Linear equations)

Linear Equations in one Variable Exercise 14A – Selina Concise Mathematics Class 8 ICSE Solutions

Solve the following equations:
Question 1.
20 = 6 + 2x
Solution:

Question 2.
15 + x = 5x + 3
Solution:

Question 3.
\(\frac { 3x+2 }{ x-6 }\) = -7
Solution:

Question 4.
3a – 4 = 2(4 – a)
Solution:

Question 5.
3(b – 4) = 2(4 – b)
Solution:

Question 6.
\(\frac { x+2 }{ 9 } =\frac { x+4 }{ 11 }\)
Solution:

Question 7.
\(\frac { x-8 }{ 5 } =\frac { x-12 }{ 9 }\)
Solution:

Question 8.
5(8x + 3) = 9(4x + 7)
Solution:

Question 9.
3(x + 1) = 12 + 4(x – 1)
Solution:

Question 10.
\(\frac { 3x }{ 4 } -\frac { 1 }{ 4 } \left( x-20 \right) =\frac { x }{ 4 } +32\)
Solution:

Question 11.
\(3a-\frac { 1 }{ 5 } =\frac { a }{ 5 } +5\frac { 2 }{ 5 }\)
Solution:

Question 12.
\(\frac { x }{ 3 } -2\frac { 1 }{ 2 } =\frac { 4x }{ 9 } -\frac { 2x }{ 3 }\)
Solution:

Question 13.
\(\frac { 4\left( y+2 \right) }{ 5 } =7+\frac { 5y }{ 13 }\)
Solution:

Question 14.
\(\frac { a+5 }{ 6 } -\frac { a+1 }{ 9 } =\frac { a+3 }{ 4 }\)
Solution:

Question 15.
\(\frac { 2x-13 }{ 5 } -\frac { x-3 }{ 11 } =\frac { x-9 }{ 5 } +1\)
Solution:

Question 16.
6(6x – 5) – 5 (7x – 8) = 12 (4 – x) + 1
Solution:

Question 17.
(x – 5) (x + 3) = (x – 7) (x + 4)
Solution:

Question 18.
(x – 5)² – (x + 2)² = -2
Solution:

Question 19.
(x – 1) (x + 6) – (x – 2) (x – 3) = 3
Solution:

Question 20.
\(\frac { 3x }{ x+6 } -\frac { x }{ x+5 } =2\)
Solution:

Question 21.
\(\frac { 1 }{ x-1 } +\frac { 2 }{ x-2 } =\frac { 3 }{ x-3 }\)
Solution:

Question 22.
\(\frac { x-1 }{ 7x-14 } =\frac { x-3 }{ 7x-26 }\)
Solution:

Question 23.
\(\frac { 1 }{ x-1 } -\frac { 1 }{ x } =\frac { 1 }{ x+3 } -\frac { 1 }{ x+4 }\)
Solution:

Question 24.
Solve: \(\frac { 2x }{ 3 } -\frac { x-1 }{ 6 } +\frac { 7x-1 }{ 4 } =2\frac { 1 }{ 6 }\)
Hence, find the value of ‘a’, if \(\frac { 1 }{ a }\) + 5x = 8.
Solution:

Question 25.
Solve: \(\frac { 4-3x }{ 5 } +\frac { 7-x }{ 3 } +4\frac { 1 }{ 3 } =0\)
Hence find the value of ‘p’ if 2p – 2x + 1 = 0
Solution:

Question 26.
Solve: \(0.25+\frac { 1.95 }{ x } =0.9\)
Solution:

Question 27.
Solve: \(5x-\left( 4x+\frac { 5x-4 }{ 7 } \right) =\frac { 4x-14 }{ 3 }\)
Solution:

Linear Equations in one Variable Exercise 14B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Fifteen less than 4 times a number is 9. Find the number.
Solution:

Question 2.
If Megha’s age is increased by three times her age, the result is 60 years. Find her age
Solution:

Question 3.
28 is 12 less than 4 times a number. Find the number.
Solution:

Question 4.
Five less than 3 times a number is -20. Find the number.
Solution:

Question 5.
Fifteen more than 3 times Neetu’s age is the same as 4 times her age. How old is she?
Solution:

Question 6.
A number decreased by 30 is the same as 14 decreased by 3 times the number; Find the number.
Solution:

Question 7.
A’s salary is same as 4 times B’s salary. If together they earn Rs.3,750 a month, find the salary of each.
Solution:

Question 8.
Separate 178 into two parts so that the first part is 8 less than twice the second part.
Solution:

Question 9.
Six more than one-fourth of a number is two-fifth of the number. Find the number.
Solution:

Question 10.
The length of a rectangle is twice its width. If its perimeter is 54 cm; find its length.
Solution:

Question 11.
A rectangle’s length is 5 cm less than twice its width. If the length is decreased by 5 cm and width is increased by 2 cm; the perimeter of the resulting rectangle will be 74 cm. Find the length and the width of the origi¬nal rectangle.
Solution:

Question 12.
The sum of three consecutive odd numbers is 57. Find the numbers.
Solution:

Question 13.
A man’s age is three times that of his son, and in twelve years he will be twice as old as his son would be. What are their present ages.
Solution:

Question 14.
A man is 42 years old and his son is 12 years old. In how many years will the age of the son be half the age of the man at that time?
Solution:

Question 15.
A man completed a trip of 136 km in 8 hours. Some part of the trip was covered at 15 km/hr and the remaining at 18 km/hr. Find the part of the trip covered at 18 km/hr.
Solution:

Question 16.
The difference of two numbers is 3 and the difference of their squares is 69. Find the numbers.
Solution:

Question 17.
Two consecutive natural numbers are such that one-fourth of the smaller exceeds one-fifth of the greater by 1. Find the numbers.
Solution:

Question 18.
Three consecutive whole numbers are such that if they are divided by 5, 3 and 4 respectively; the sum of the quotients is 40. Find the numbers.
Solution:

Question 19.
If the same number be added to the numbers 5, 11, 15 and 31, the resulting numbers are in proportion. Find the number.
Solution:

Question 20.
The present age of a man is twice that of his son. Eight years hence, their ages will be in the ratio 7 : 4. Find their present ages.
Solution:

Linear Equations in one Variable Exercise 14C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Solve:
(i) \(\frac { 1 }{ 3 } x-6=\frac { 5 }{ 2 }\)
(ii) \(\frac { 2x }{ 3 } -\frac { 3x }{ 8 } =\frac { 7 }{ 12 }\)
(iii) (x + 2)(x + 3) + (x – 3)(x – 2) – 2x(x + 1) = 0
(iv) \(\frac { 1 }{ 10 } -\frac { 7 }{ x } =35\)
(v) 13(x – 4) – 3(x – 9) – 5(x + 4) = 0
(vi) x + 7 – \(\frac { 8x }{ 3 } =\frac { 17x }{ 6 } -\frac { 5x }{ 8 }\)
(vii) \(\frac { 3x-2 }{ 4 } -\frac { 2x+3 }{ 3 } =\frac { 2 }{ 3 } -x\)
(viii) \(\frac { x+2 }{ 6 } -\left( \frac { 11-x }{ 3 } -\frac { 1 }{ 4 } \right) =\frac { 3x-4 }{ 12 }\)
(ix) \(\frac { 2 }{ 5x } -\frac { 5 }{ 3x } =\frac { 1 }{ 15 }\)
(x) \(\frac { x+2 }{ 3 } -\frac { x+1 }{ 5 } =\frac { x-3 }{ 4 } -1\)
(xi) \(\frac { 3x-2 }{ 3 } +\frac { 2x+3 }{ 2 } =x+\frac { 7 }{ 6 }\)
(xii) \(x-\frac { x-1 }{ 2 } =1-\frac { x-2 }{ 3 }\)
(xiii) \(\frac { 9x+7 }{ 2 } -\left( x-\frac { x-2 }{ 7 } \right) =36\)
(xiv) \(\frac { 6x+1 }{ 2 } +1=\frac { 7x-3 }{ 3 }\)
Solution:

Question 2.
After 12 years, I shall be 3 times as old as 1 was 4 years ago. Find my present age.
Solution:

Question 3.
A man sold an article for 7396 and gained 10% on it. Find the cost price of the article
Solution:

Question 4.
The sum of two numbers is 4500. If 10% of one number is 12.5% of the other, find the numbers.
Solution:

Question 5.
The sum of two numbers is 405 and their ratio is 8 : 7. Find the numbers.
Solution:

Question 6.
The ages of A and B are in the ratio 7 : 5. Ten years hence, the ratio of their ages will be 9 : 7. Find their present ages.
Solution:

Question 7.
Find the number whose double is 45 greater than its half.
Solution:

Question 8.
The difference between the squares of two consecutive numbers is 31. Find the numbers.
Solution:

Question 9.
Find a number such that when 5 is subtracted from 5 times the number, the result is 4 more than twice the number.
Solution:

Question 10.
The numerator of a fraction is 5 less than its denominator. If 3 is added to the numerator, and denominator both, the fraction becomes \(\frac { 2 }{ 3 }\). Find the original fraction.
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Publishers Concise Biology Class 7 ICSE Solutions Chapter 1 Plant And Animal Tissues

Selina Concise Biology Class 7 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 16 Pythagoras Theorem

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 16 Pythagoras Theorem

Pythagoras Theorem Exercise 16 – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Solution:

Question 2.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
Solution:

Question 3.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if:
PQ = 34 cm and QR = 33.6 cm.
Solution:

Question 4.
The sides of a certain triangle are given below. Find, which of them is right-triangle
(i) 16 cm, 20 cm and 12 cm
(ii) 6 m, 9 m and 13 m
Solution:

Question 5.
In the given figure, angle BAC = 90°, AC = 400 m and AB = 300 m. Find the length of BC.

Solution:

Question 6.
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD
Solution:

Question 7.
In triangle PQR, angle Q = 90°, find :
(i) PR, if PQ = 8 cm and QR = 6 cm
(ii) PQ, if PR = 34 cm and QR = 30 cm
Solution:

Question 8.
Show that the triangle ABC is a right-angled triangle; if:
AB = 9 cm, BC = 40 cm and AC = 41 cm
Solution:

Question 9.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

Solution:

Question 10.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

Solution:

Question 11.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

Solution:

Question 12.
A ladder, 6.5 m long, rests against a vertical wall. Ifthe foot of the ladcler is 2.5 m from the foot of the wall, find upto how much height does the ladder reach?
Solution:

Question 13.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Solution:

Question 14.
Use the information given in the figure to find the length AD.

Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 12 Algebraic Identities

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 12 Algebraic Identities

Algebraic Identities Exercise 12A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Use direct method to evaluate the following products :
(i) (x + 8)(x + 3)
(ii) (y + 5)(y – 3)
(iii) (a – 8)(a + 2)
(iv) (b – 3)(b – 5)
(v) (3x – 2y)(2x + y)
(vi) (5a + 16)(3a – 7)
(vii) (8 – b) (3 + b)
Solution:

Question 2.
Use direct method to evaluate :

Solution:

Question 3.
Evaluate :

Solution:

Question 4.
Use the product (a + b) (a – b) = a² – b² to evaluate:
(i) 21 × 19
(ii) 33 × 27
(iii) 103 × 97
(iv) 9.8 × 10.2
(v) 7.7 × 8.3
(vi) 4.6 × 5.4
Solution:

Question 5.
Evaluate :
(i) (6 – xy) (6 + xy)

Solution:

Algebraic Identities Exercise 12B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Expand :
(i) (2a + b)²
(ii) (a – 2b)²

Solution:

Question 2.
Find the square of :

Solution:

Question 3.
Evaluate:
Using expansion of (a + b)² or (a – b)²
(i) (208)²
(ii) (92)²
(iii)(415)²
(iv) (188)²
(v) (9.4)²
(vi) (20.7)²
Solution:

Question 4.
Expand :

Solution:

Question 5.
Find the cube of :

Solution:

Algebraic Identities Exercise 12C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
If a  +b = 5 and ab = 6; find a² + b²
Solution:

Question 2.
If a – b = 6 and ab = 16; find a² + b²
Solution:

Question 3.
If a² + b² = 29 and ab = 10 ; find :
(i) a + b
(ii) a – b
Solution:

Question 4.
If a² + b² = 10 and ab = 3; find :
(i) a – b
(ii) a + b
Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.
If a + b + c = 10 and a² + b² + c² = 38; find ab + bc + ca
Solution:

Question 10.
Find a² + b² + c² ; if a + b + c = 9 and ab + bc + ca = 24
Solution:

Question 11.
Find a + b + c; if a² + b² + c² = 83 and ab + bc + ca = 71
Solution:

Question 12.
If a + b = 6 and ab=8; find a³ + b³
Solution:

Question 13.
If a – b = 3 and ab = 10; find a³ – b³
Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.
The sum of the squares of two numbers is 13 and their product is 6. Find:
(i) the sum of the two numbers.
(ii) the difference between them.
Solution:

Algebraic Identities Exercise 12D – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Evaluate:

Solution:

Question 2.
Evaluate:

Solution:

Question 3.
Find the square of :

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.
If a² + b² = 41 and ab = 4, find :
(i) a – b
(ii) a + b
Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.
Expand :
(i) (3x – 4y + 5z)²
(ii) (2a – 5b – 4c)²
(iii) (5x + 3y)³
(iv) (6a – 7b)³
Solution:

Question 10.
If a + b + c = 9 and ab + bc + ca = 15, find: a² + b² + c².
Solution:

Question 11.
If a + b + c = 11 and a² + b² + c² = 81, find ab + bc + ca.
Solution:

Question 12.
If 3x – 4y = 5 and xy = 3, find : 27x³ – 64y³.
Solution:

Question 13.
If a + b = 8 and ab = 15, find : a³ + b³.
Solution:

Question 14.
If 3x + 2y = 9 and xy = 3, find : 27x³ + 8y³
Solution:

Question 15.
If 5x – 4y = 7 and xy = 8, find : 125x³ – 64y³
Solution:

Question 16.
The difference between two numbers is 5 and their products is 14. Find the difference between their cubes.
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 15 Triangles

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 15 Triangles

Triangles Exercise 15A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Stale, if the triangles are possible with the following angles :
(i) 20°, 70° and 90°
(ii) 40°, 130° and 20°
(iii) 60°, 60° and 50°
(iv) 125°, 40° and 15°
Solution:

Question 2.
If the angles of a triangle are equal, find its angles.
Solution:

Question 3.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
Solution:

Question 4.
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Solution:

Question 5.
Calculate the unknown marked angles in each figure :

Solution:

Question 6.
Find the value of each angle in the given figures:

Solution:

Question 7.
Find the unknown marked angles in the given figure:

Solution:

Question 8.
In the given figure, show that: ∠a = ∠b + ∠c

(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
Solution:

Question 9.
Calculate the angles of a triangle if they are in the ratio 4 : 5 : 6.
Solution:

Question 10.
One angle of a triangle is 60°. The, other two angles are in the ratio of 5 : 7. Find the two angles.
Solution:

Question 11.
One angle of a triangle is 61° and the other two angles are in the ratio 1\(\frac { 1 }{ 2 }\) : 1 \(\frac { 1 }{ 3 }\). Find these angles.
Solution:

Question 12.
Find the unknown marked angles in the given figures :

Solution:

Triangles Exercise 15B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Find the unknown angles in the given figures:

Solution:

Question 2.
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figures :

Solution:

Question 3.
The angle of vertex of an isosceles triangle is 100°. Find its base angles.
Solution:

Question 4.
One of the base angles of an isosceles triangle is 52°. Find its angle of vertex.
Solution:

Question 5.
In an isosceles triangle, each base angle is four times of its vertical angle. Find all the angles of the triangle.
Solution:

Question 6.
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
Solution:

Question 7.
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
Solution:

Question 8.
The vertical angle of an isosceles triangle is three times the sum of its base angles. Find each angle.
Solution:

Question 9.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1 : 4. Find each angle of the triangle.
Solution:

Question 10.
In the given figure, BI is the bisector of∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.

Solution:

Question 11.
In the given figure, express a in terms of b.

Solution:

Question 12.
(a) In Figure (i) BP bisects ∠ABC and AB = AC. Find x.
(b) Find x in Figure (ii) Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.

Solution:

Question 13.
In each figure, given below, ABCD is a square and ∆ BEC is an equilateral triangle.
Find, in each case : (i) ∠ABE(ii) ∠BAE

Solution:

Question 14.
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.

Solution:

Triangles Exercise 15C – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Construct a ∆ABC such that:
(i) AB = 6 cm, BC = 4 cm and CA = 5.5 cm
(ii) CB = 6.5 cm, CA = 4.2 cm and BA = 51 cm
(iii) BC = 4 cm, AC = 5 cm and AB = 3.5 cm
Solution:

Question 2.
Construct a A ABC such that:
(i) AB = 7 cm, BC = 5 cm and ∠ABC = 60°
(ii) BC = 6 cm, AC = 5.7 cm and ∠ACB = 75°
(iii) AB = 6.5 cm, AC = 5.8 cm and ∠A = 45°
Solution:

Question 3.
Construct a ∆ PQR such that :
(i) PQ = 6 cm, ∠Q = 60° and ∠P = 45°. Measure ∠R.
(ii) QR = 4.4 cm, ∠R = 30° and ∠Q = 75°. Measure PQ and PR.
(iii) PR = 5.8 cm, ∠P = 60° and ∠R = 45°.
Measure ∠Q and verify it by calculations
Solution:

Question 4.
Construct an isosceles A ABC such that:
(i) base BC = 4 cm and base angle = 30°
(ii) base AB = 6-2 cm and base angle = 45°
(iii) base AC = 5 cm and base angle = 75°.
Measure the other two sides of the triangle.
Solution:

Question 5.
Construct an isosceles ∆ABC such that:
(i) AB = AC = 6.5 cm and ∠A = 60°
(ii) One of the equal sides = 6 cm and vertex angle = 45°. Measure the base angles.
(iii) BC = AB = 5-8 cm and ZB = 30°. Measure ∠A and ∠C.
Solution:

Question 6.
Construct an equilateral A ABC such that:
(i) AB = 5 cm. Draw the perpendicular bisectors of BC and AC. Let P be the point of intersection of these two bisectors. Measure PA, PB and PC.
(ii) Each side is 6 cm.
Solution:

Question 7.
(i) Construct a ∆ ABC such that AB = 6 cm, BC = 4.5 cm and AC = 5.5 cm. Construct a circumcircle of this triangle.
(ii) Construct an isosceles ∆PQR such that PQ = PR = 6.5 cm and ∠PQR = 75°. Using ruler and compasses only construct a circumcircle to this triangle.
(iii) Construct an equilateral triangle ABC such that its one side = 5.5 cm.
Construct a circumcircle to this triangle.
Solution:

Question 8.
(i) Construct a ∆ABC such that AB = 6 cm, BC = 5.6 cm and CA = 6.5 cm. Inscribe a circle to this triangle and measure its radius.
(ii) Construct an isosceles ∆ MNP such that base MN = 5.8 cm, base angle MNP = 30°. Construct an incircle to this triangle and measure its radius.
(iii) Construct an equilateral ∆DEF whose one side is 5.5 cm. Construct an incircle to this triangle.
(iv) Construct a ∆ PQR such that PQ = 6 cm, ∠QPR = 45° and angle PQR = 60°. Locate its incentre and then draw its incircle.
Solution:

Selina Concise Mathematics Class 7 ICSE Solutions