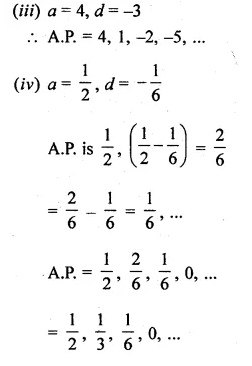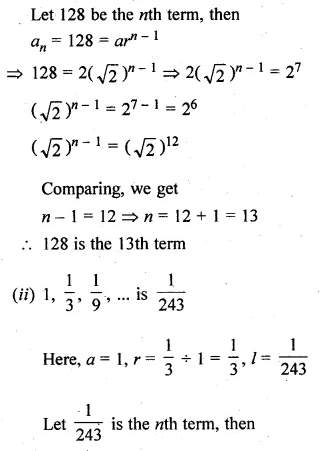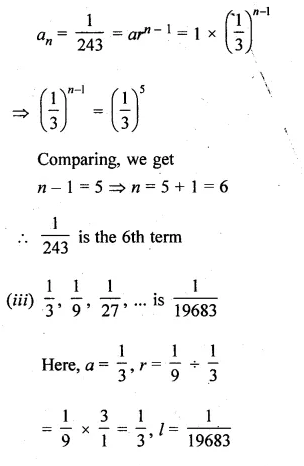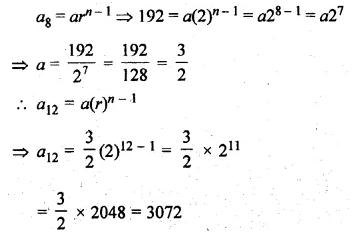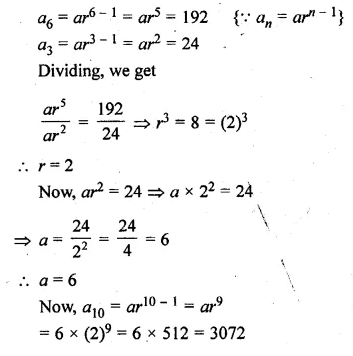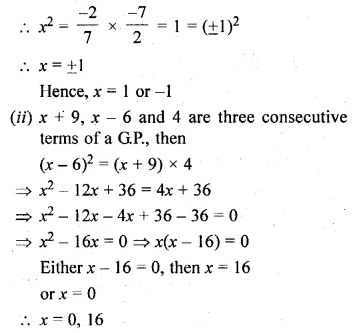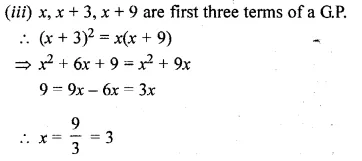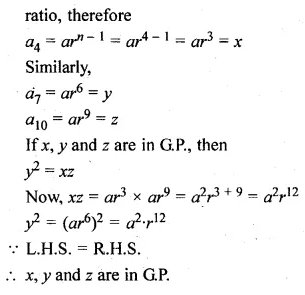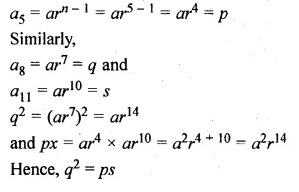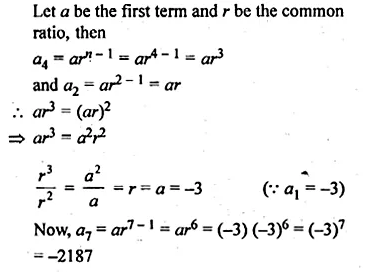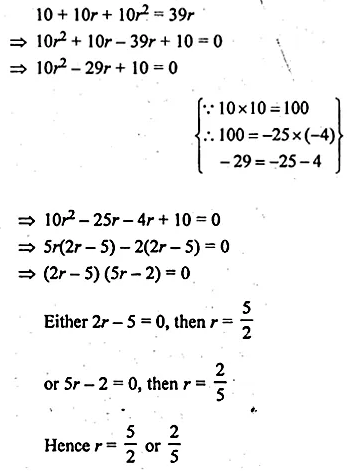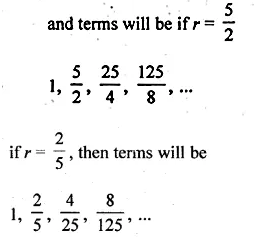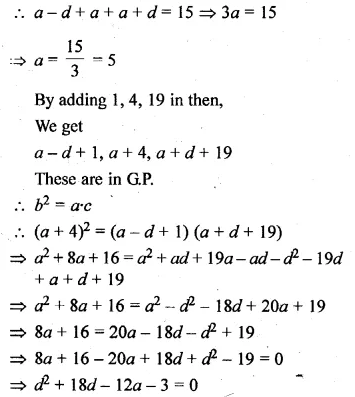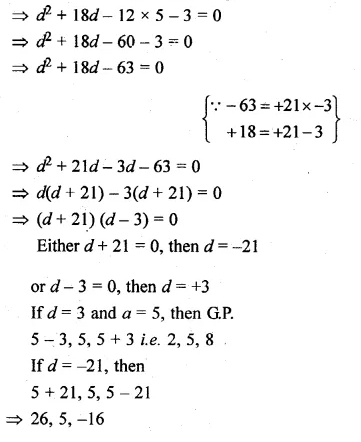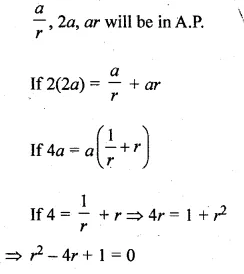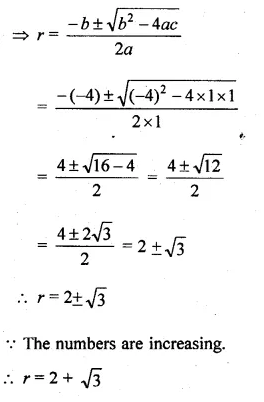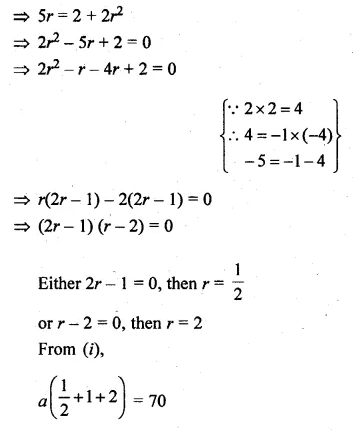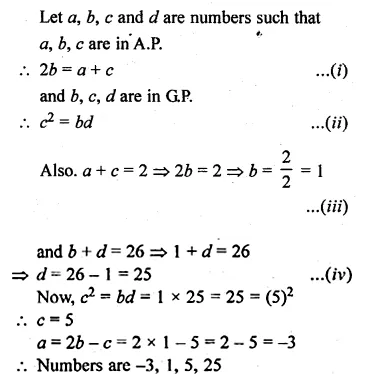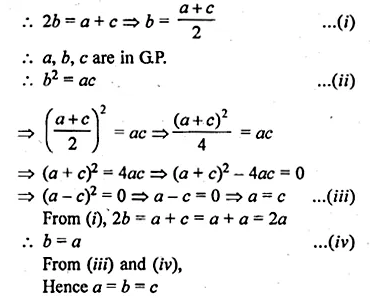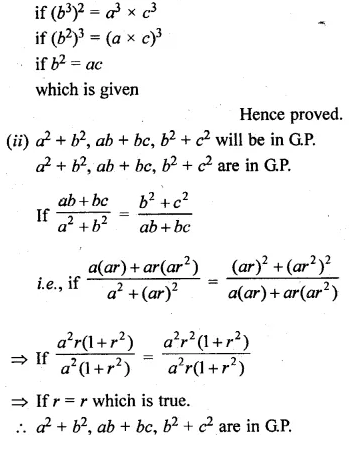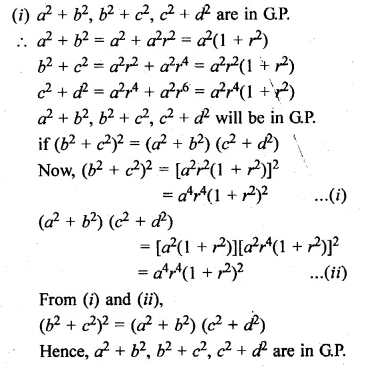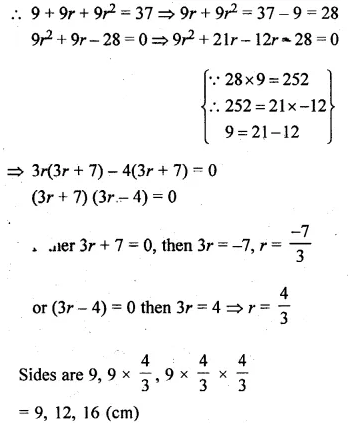Prasanna

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the A.P. whose nth term is 7 – 3K. Also find the 20th term.
Solution:
T_n = 7 – 3n
Giving values 1, 2, 3, 4, … to n, we get
T₁ = 7 – 3 x 1 = 7 – 3 = 4
T₂ = 7 – 3 x 2 = 7 – 6 = 1
T₃ = 7 – 3 x 3 = 7 – 9 = -2
T₄ = 7 – 3 x 4 = 7 – 12 = -5
T₂₀ = 7 – 3 x 20 = 7 – 60 = -53
A.P. is 4, 1, -2, -5, …
20th term = -53

Question 2.
Find the indicated terms in each of following A.P.s:
(i) 1, 6, 11, 16, …; a₂₀
(ii) – 4, – 7, – 10, – 13, …, a₂₅, a_n
Solution:
(i) 1, 6, 11, 16, …
Here, a = 1, d = 6 – 1 – 5
a₂₀ = a + (n – 1 )d
= 1 + (20 – 1) x 5
= 1 + 19 x 5
= 1 + 95
= 96

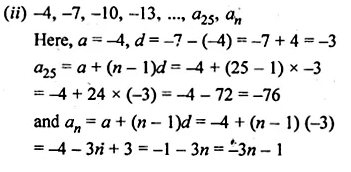
Question 3.
Find the nth term and the 12th term of the list of numbers: 5, 2, – 1, – 4, …
Solution:
5, 2, -1, -4, …
Here, a = 5 d = 2 – 5 = -3
(i) T_n = a + (n – 1)d
= 5 + (n – 1) (-3)
= 5 – 3n + 3
= 8 – 3n
(ii) T₁₂ = a + 11d
= 5 + 11(-3)
= 5 – 33
= -28

Question 4.
Find the 8th term of the A.P. whose first term is 7 and common difference is 3.
Solution:
First term (a) = 7
and common difference (d) = 3
A.P. = 7, 10, 13, 16, 19, …
T₈ = a + (n – 1)d
= 7 + (8 – 1) x 3
= 7 + 7 x 3
= 7 + 21
= 28

Question 5.
(i) If the common difference of an A.P. is – 3 and the 18th term is – 5, then find its first term.
(ii) If the first term of an A.P. is – 18 and its 10th term is zero, then find its common difference.
Solution:
(i) Common difference (d) = -3
T₁₈ = -5
a + (n – 1 )d = Tn
a + (18 – 1) (-3) = -5

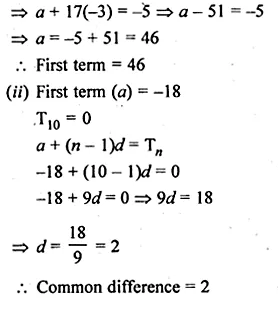
Question 6.
Which term of the A.P.
(i) 3, 8, 13, 18, … is 78?
(ii) 7, 13, 19, … is 205 ?
(iii) 18, \(15 \frac { 1 }{ 2 } \), 13, … is – 47 ?
Solution:
(i) 3, 8, 13, 18, … is 78
Let 78 is nth term
Here, a = 3, d = 8 – 3 = 5

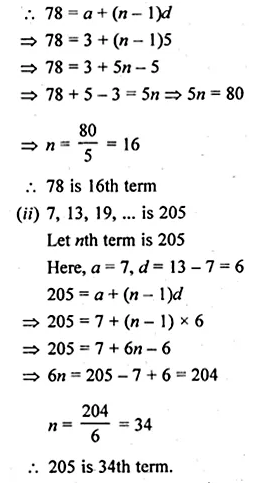
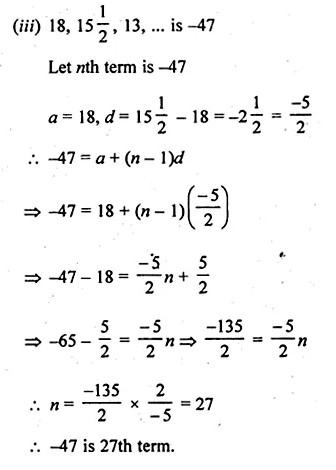
Question 7.
(i) Check whether – 150 is a term of the A.P. 11, 8, 5, 2, …
(ii) Find whether 55 is a term of the A.P. 7, 10, 13, … or not. If yes, find which term is it.
(iii) Is 0 a term of the A.P. 31,28, 25,…? Justify your answer.
Solution:
(i) A.P. is 11, 8, 5, 2, …
Here, a = 11, d = 8 – 11 = -3
Let -150 = n, then

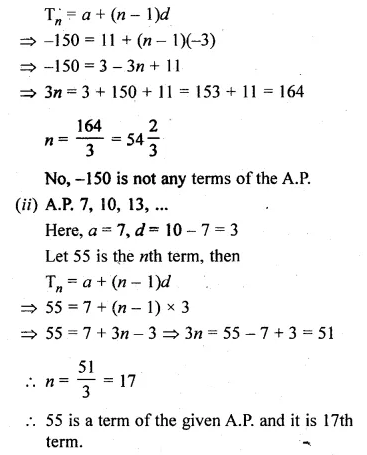
Question 8.
(i) Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.
(ii) Find the 12th from the end of the A.P. – 2, – 4, – 6, …; – 100.
Solution:
(i) A.P. is 3, 8, 13, …, 253
12th term from the end
Last term = 253
Here, a = 3, d = 8 – 3 = 5

Question 9.
Find the sum of the two middle most terms of the A.P.
\(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)
Solution:
Given
A.P. is \(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)

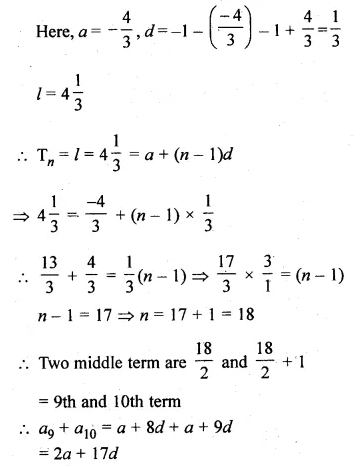
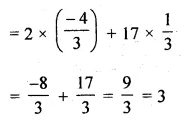
Question 10.
Which term of the A.P. 53, 48, 43,… is the first negative term ?
Solution:
Let nth term is the first negative term of the A.P. 53, 48, 43, …
Here, a = 53, d = 48 – 53 = -5
.’. T_n = a + (n – 1 )d
= 53 + (n – 1) x (-5)
= 53 – 5n + 5
= 58 – 5n
5n = 58
\(n= \frac { 58 }{ 5 } \)
= \(11 \frac { 3 }{ 5 } \)
∴ 12th term will be negative.

Question 11.
Determine the A.P. whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20.
Solution:
In an A.P.,
T₅ = 19
T₁₃ – T₈ = 20
Let a be the first term and d be the common difference

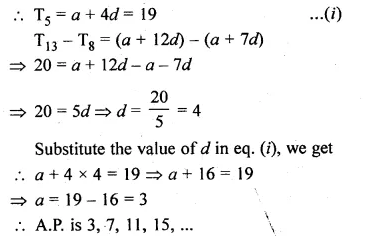
Question 12.
Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12
Solution:
T₃ = 16
T₇ – T₅ = 12
Let a be the first term and d be the common difference

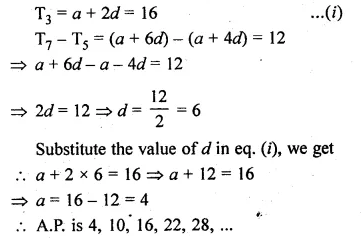
Question 13.
Find the 20th term of the A.P. whose 7th term is 24 less than the 11th term, first term being 12.
Solution:
T₁₁ – T₇ = 24
a= 12
Let a be the first term and d be the common difference, then
(a + 10d) – (a + 6d) = 24

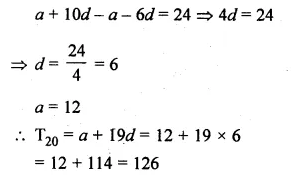
Question 14.
Find the 31st term of an A.P. whose 11th term is 38 and 6th term is 73.
Solution:
T₁₁ = 38, T₆ = 73
Let a be the first term and d be the common difference, then
a + 10d = 38..(i)
a + 5d = 73…(ii)

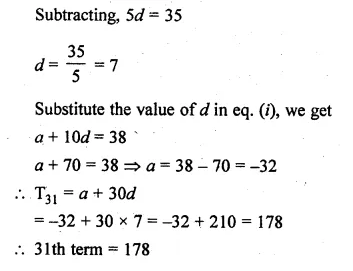
Question 15.
If the seventh term of an A.P. is \(\\ \frac { 1 }{ 9 } \) and its ninth term is \(\\ \frac { 1 }{ 7 } \), find its 63rd term.
Solution:
a₇ = \(\\ \frac { 1 }{ 9 } \)
⇒ a + 6d = \(\\ \frac { 1 }{ 9 } \) ….(i)
a₉ = \(\\ \frac { 1 }{ 7 } \)
⇒ a + 8d = \(\\ \frac { 1 }{ 7 } \)……(ii)

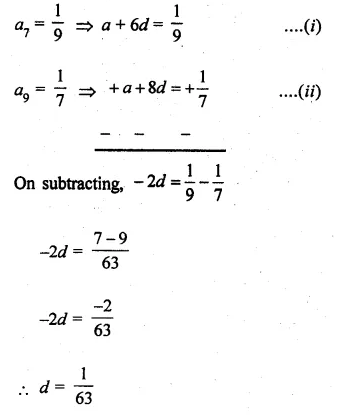
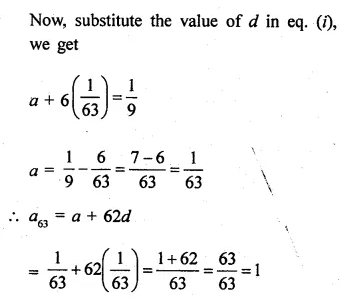
Question 16.
(i) The 15th term of an A.P. is 3 more than twice its 7th term. If the 10th term of the A.P. is 41, find its nth term.
(ii) The sum of 5th and 7th terms of an A.P. is 52 and the 10th term is 46. Find the A.P.
(iii) The sum of 2nd and 7th terms of an A.P. is 30. If its 15th term is 1 less than twice its 8th term, find the A.P.
Solution:
(i) Let a be the first term and d be a common difference.
We have,



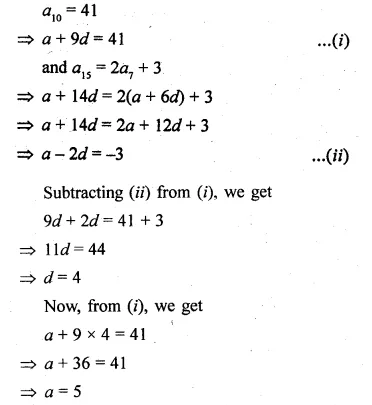
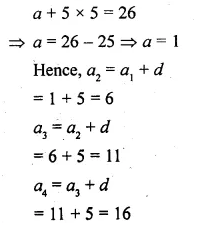
∴ The A.P formed is 1, 6, 11, 16,….

Question 17.
If 8th term of an A.P. is zero, prove that its 38th term is triple of its 18th term.
Solution:
T₈ = 0
To prove that T₃₈ = 3 x T₁₈
Let a be the first term and d be the common difference

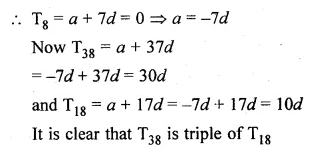
Question 18.
Which term of the A.P. 3, 10, 17,… will be 84 more than its 13th term?
Solution:
A.P. is 3, 10, 17, …
Here, a = 3, d – 10 – 3 = 7
T₁₃ = a + 12d
= 3 + 12 x 7
= 3 + 84
= 87

Question 19.
If the nth terms of the two A.g.s 9, 7, 5, … and 24, 21, 18, … are the same, find the value of n. Also, find that term
Solution:
nth term of two A.P.s 9, 7, 5,… and 24, 21, 18, … are same
In the first A.P. 9, 7, 5, …
a = 9 and d = 7 – 9 = -2
T_n = a + (n – 1)d
= 9 + (n – 1)(-2)

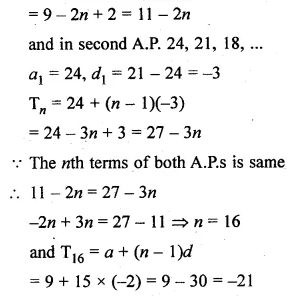
Question 20.
(i) How many two digit numbers are divisible by 3 ?
(ii) Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
(iii) How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3?
Solution:
(i) Two digits numbers divisible by 3 are
12, 15, 18, 21, …, 99
Here, a = 13, d = 15 – 12 = 3 and l = 99
Let number divisible by 3 and n

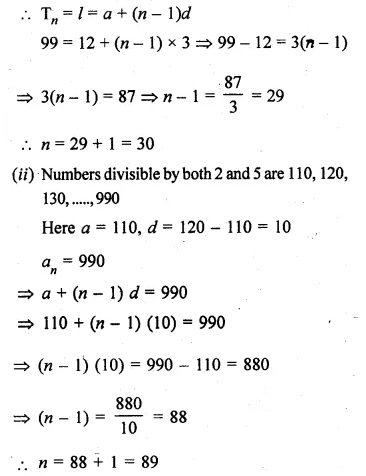
Question 21.
If the numbers n – 2, 4n – 1 and 5n + 2 are in A.P., find the value of n.
Solution:
n – 2, 4n – 1 and 5n + 2 are in A.P.
∴ 2(4n – 1) = n – 2 + 5n + 2
8n – 2 = 6n
⇒ 8n – 6n = 2
⇒ 2n = 1
⇒ \(n \frac { 2 }{ 2 } \) = 1
∴ n = 1

Question 22.
The sum of three numbers in A.P. is 3 and their product is – 35. Find the numbers.
Solution:
Sum of three numbers which are in A.P. = 3
Their product = -35
Let three numbers which are in A.P.
a – d, a, a + d
a – d + a + a + d = 3
⇒ 3a = 3 ,
⇒ a = \(\\ \frac { 3 }{ 3 } \) = 1

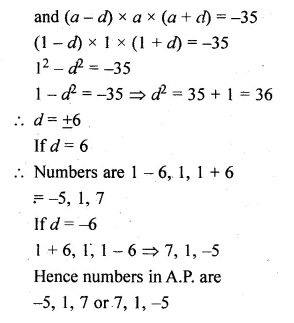
Question 23.
The sum of three numbers in A.P. is 30 and the ratio of first number to the third number is 3 : 7. Find the numbers.
Solution:
Sum of three numbers in A.P. = 30
Ratio between first and the third number = 3 : 7
Let numbers be
a – d, a, a + d, then
a – d + a + a + d = 30

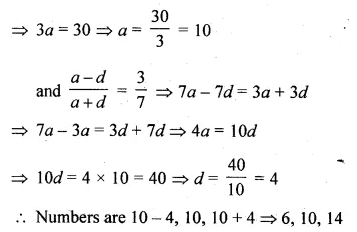
Question 24.
The sum of the first three terms of an A.P.is 33. If the product of the first and the third terms exceeds the second term by 29, find the A.P.
Solution:
Let the three numbers in A.P. are
a – d, a, a + d
Now, a – d + a + a + d = 33
⇒ 3a = 33
⇒ a = \(\\ \frac { 33 }{ 3 } \) = 11

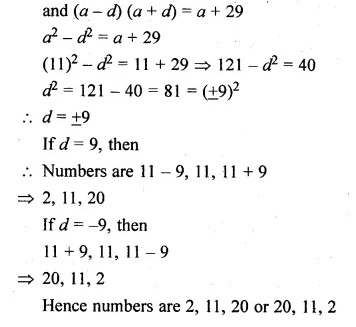
Question 25.
A man starts repaying a loan as first instalment of Rs 500. If he increases the instalment by Rs 25 every month, what,amount will he pay in the 30th instalment?
Solution:
First instalment of loan = Rs 500
Increases Rs 25 every month
Here, a = 500, d = 25
Total instalments (n) = 30
We have to find T₃₀
T₃₀ = a + (n – 1 )d = a + 29d
= 500 + 29 x 25
= 500 + 725
= Rs 1225

Question 26.
Ramkali saved Rs 5 in the first week of a year and then increased her savings by Rs 1.75. If in the rcth week, her weekly savings become Rs 20.75, find n.
Solution:
Savings in the first week = Rs 5
Increase every week = Rs 1.75
No. of weeks = n

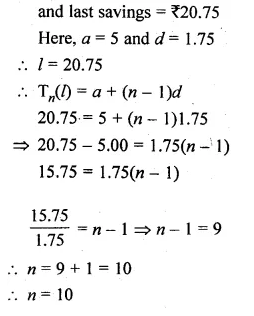
Question 27.
Justify whether it is true to say that the following are the nth terms of an A.P.
(i) 2n – 3
(ii) n² + 1
Solution:
(i) 2n – 3
Giving the some difference values to n such as 1, 2, 3, 4, … then
2 x 1 – 3 = 2 – 3 = -1
2 x 2 – 3 = 4 – 3 = 1
2 x 3 – 3 = 6 – 3 = 3
2 x 4 – 3 = 8 – 3 = 5

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
For the following A.P.s, write the first term a and the common difference d:
(i) 3, 1, – 1, – 3, …
(ii) \(\frac { 1 }{ 3 } ,\frac { 5 }{ 3 } ,\frac { 9 }{ 3 } ,\frac { 13 }{ 3 } ,…. \)
(iii) – 3.2, – 3, – 2.8, – 2.6, …
Solution:
(i) 3, 1, -1, -3, …
Here first term (a) = 3
and the common difference (d)
= 1 – 3 = -2,
– 1 – 1 = -2,…
= -2

Question 2.
Write first four terms of the A.P., when the first term a and the common difference d are given as follows :
(i) a = 10, d = 10
(ii) a = – 2, d = 0
(iii) a = 4, d = – 3
(iv) a = \(\\ \frac { 1 }{ 2 } \), d = \(– \frac { 1 }{ 2 } \)
Solution:
(i) a = 10, d = 10
∴ A.P. = 10, 20, 30, 40, …
(ii) a = -2, d = 0
∴ A.P. = -2, -2, -2, -2, ….

Question 3.
Which of the following lists of numbers form an A.P.? If they form an A.P., find the common difference d and write the next three terms :
(i) 4, 10, 16, 22,…
(ii) – 2, 2, – 2, 2,…..
(iii) 2, 4, 8, 16,….
(iv) 2, \(\\ \frac { 5 }{ 2 } \), 3, \(\\ \frac { 7 }{ 2 } \),……
(v) – 10, – 6, – 2, 2,….
(vi) 1², 3², 5², 7²,….
(vii) 1, 3, 9, 27,….
(viii) √2, √8, √18, √32,….
(ix) 3, 3 + √2, 3 + √2, 3 + 3√2,…..
(x) √3, √6, √9, √12,……
(xi) a, 2a, 3a, 4a,…….
(xii) a, 2a + 1, 3a + 2, 4a + 3,….
Solution:
(i) 4, 10, 16, 22,…
Here a = 4, d = 10 – 4 = 6, 16 – 10 = 6, 22 – 16 = 6
∵ common difference is same
∵ It is in A.P
and next three terms are 28, 34, 40

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Choose the correct answer from the given four options (1 to 33) :

Question 1.
The list of numbers – 10, – 6, – 2, 2, … is
(a) an A.P. with d = – 16
(b) an A.P with d = 4
(c) an A.P with d = – 4
(d) not an A.P
Solution:
-10, -6, -2, 2, … is
an A.P. with d = – 6 – (-10)
= -6 + 10 = 4 (b)

Question 2.
The 10th term of the A.P. 5, 8, 11, 14, … is
(a) 32
(b) 35
(c) 38
(d) 185
Solution:
10th term of A.P. 5, 8, 11, 14, …
{∵ a = 5, d = 3}
a + (n – 1)d = 5 + (10 – 1) x 3
= 5 + 9 x 3
= 5 + 27
= 32 (a)

Question 3.
The 30th term of the A.P. 10, 7, 4, … is
(a) 87
(b) 77
(c) – 77
(d) – 87
Solution:
30th term of A.P. 10, 7, 4, … is
30th term = a + (n – 1)d

Question 4.
The 11th term of the A.P. – 3, \(– \frac { 1 }{ 2 } \), 2, … is
(a) 28
(b) 22
(c) – 38
(d) – 48
Solution:
Given
-3, \(– \frac { 1 }{ 2 } \), 2, …

Question 5.
The 4th term from the end of the A.P. – 11, – 8, – 5, …, 49 is
(a) 37
(b) 40
(c) 43
(d) 58
Solution:
4th term from the end of the A.P. -11, -8, -5, …, 49 is
Here, a = -11, d = -8 – (-11) = -8 + 11 = 3 and l = 49 .

Question 6.
The 15th term from the last of the A.P. 7, 10, 13, …,130 is
(a) 49
(b) 85
(c) 88
(d) 110
Solution:
15th term from the end of A.P. 7, 10, 13,…, 130
Here, a = 7, d = 10 – 7 = 3, l = 130
15th term from the end = l – (n – 1)d
= 130 – (15 – 1) x 3
= 130 – 42
= 88 (c)

Question 7.
If the common difference of an A.P. is 5, then a₁₈ – a₁₃ is
(a) 5
(b) 20
(c) 25
(d) 30
Solution:
Common difference of an A.P. (d) = 5
a₁₈ – a₁₃ = a + 17d – a – 12d = 5d = 5 x 5 = 25 (c)

Question 8.
In an A.P., if a₁₈ – a₁₄ = 32 then the common difference is
(a) 8
(b) – 8
(c) – 4
(d) 4
Solution:
If a₁₈ – a₁₄ = 32, then d = ?
(a + 17d) – a – 13d = 32
⇒ a + 17d – a – 13d = 32
⇒ 4d = 32
⇒ \(d \frac { 32 }{ 4 } \) = 8 (a)

Question 9.
In an A.P., if d = – 4, n = 7, a_n = 4, then a is
(a) 6
(d) 7
(c) 20
(d) 28
Solution:
In an A.P., d = -4, x = 7, a_n = 4 then a = ?
a_n = a(n – 1)d = 4
a₇ = a + (7 – 1)d = 4
⇒ a + 6d = 4
⇒ a + 6 x (-4) = 4
a – 24 = 4
⇒ a = 4 + 24 = 28 (d)

Question 10.
In an A.P., if a = 3.5, d = 0, n = 101, then a_n will be
(a) 0
(b) 3.5
(c) 103.5
(d) 104.5
Solution:
In an A.P.
a = 3.5, d= 0, n = 101, then a_n = ?
a_n = a₁₀₁ = a + (101 – 1)d
= 3.5 + 100d
= 3.5 + 100 x 0
= 3.5 + 0
= 3.5 (b)

Question 11.
In an A.P., if a = – 7.2, d = 3.6, a_n = 7.2, then n is
(a) 1
(b) 3
(c) 4
(d) 5
Solution:
In an A.P.
a = – 7.2, d = 3.6, a_n = 7.2, n = ?
a_n = 7.2
a + (n – 1)d = 7.2
– 7.2 + (n – 1) 3.6 = 7.2
(n – 1) x 3.6 = 7.2 + 7.2 = 14.4
(n – 1) = \(\\ \frac { 14.4 }{ 3.6 } \) = 4
n = 4 + 1 = 5 (d)

Question 12.
Which term of the A.P. 21, 42, 63, 84,… is 210?
(a) 9th
(b) 10th
(c) 11th
(d) 12th
Solution:
Which term of an A.P. 21, 42, 63, 84, … is 210
Let 210 be nth term, then
Here, a = 21, d = 42 – 21 =21
210 = a + (n – 1)d
210 = 21 + (n – 1) x 21
⇒ 210 – 21 = 21(n – 1)
⇒ \(\\ \frac { 189 }{ 21 } \) = n – 1
⇒ 9 = n – 1
⇒ n = 9 + 1 = 10
.’. It is 10th term. (b)

Question 13.
If the last term of the A.P. 5, 3, 1, – 1,… is – 41, then the A.P. consists of
(a) 46 terms
(b) 25 terms
(c) 24 terms
(d) 23 terms
Solution:
Last term of an A.P. 5, 3, 1, -1, … is -41
Then A.P. will consist of ……. terms
Here, a = 5, d = 3 – 5 = – 2 and n =?
l = -41
l = -41
l = -41 = a + (n – 1 )d
-41 = 5 + (n – 1) (-2)
-41 – 5 = (n – 1) (-2)
⇒ \(\\ \frac { -46 }{ -2 } \) = n – 1
⇒ n – 1 = 23
⇒ n = 23 + 1 = 24
A.P. consists of 24 terms. (c)

Question 14.
If k – 1, k + 1 and 2k + 3 are in A.P., then the value of k is
(a) – 2
(b) 0
(c) 2
(d) 4
Solution:
k – 1, k + 1 and 2k + 3 are in A.P.
2(k+ 1) = (k – 1) + (2k + 3)
⇒ 2k + 2 = k – 1 + 2k + 3
⇒ 2k + 2 – 3k + 2
⇒ 3k – 2k = 2 – 2
⇒ k = 0 (b)

Question 15.
The 21st term of an A.P. whose first two terms are – 3 and 4 is
(a) 17
(b) 137
(c) 143
(d) – 143
Solution:
First two terms of an A.P. are – 3 and 4
a = -3, d = 4 – (-3) = 4 + 3 = 7
21st term = a + 20d
= -3 + 20(7)
= -3 + 140
= 137 (b)

Question 16.
If the 2nd term of an A.P. is 13 and the 5th term is 25, then its 7th term is
(a) 30
(b) 33
(c) 37
(d) 38
Solution:
In an A.P.
2nd term = 13 ⇒ a + d = 13 …(i)
5th term = 25 ⇒ a + 4d = 25 …(ii)
Subtracting (i) and (ii),
3d = 12
⇒ d = \(\\ \frac { 1 }{ 3 } \)
Substitute the value of d in eq. (i), we get
a = 13 – 4 = 9
7th term = a + 6d = 9 + 6 x 4 = 9 + 24 = 33 (b)

Question 17.
If the first term of an A.P. is – 5 and the common difference is 2, then the sum of its first 6 terms is
(a) 0
(b) 5
(c) 6
(d) 15
Solution:
First term (a) of an A.P. = -5
Common difference (d) is 2
Sum of first 6 terms = \(\frac { n }{ 2 } \left[ 2a+\left( n-1 \right) d \right] \)
= \(\frac { 6 }{ 2 } \left[ 2\times \left( -5 \right) +\left( 6-1 \right) \times 2 \right] \)
= 3[-10 + 5 x 2]
= 3 x [-10 – 10]
= 3 x 0 = 0 (a)

Question 18.
The sum of 25 terms of the A.P.\(-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } \) is
(a) 0
(b) \(– \frac { 2 }{ 3 } \)
(c) \(– \frac { 50 }{ 3 } \)
(d) – 50
Solution:
Sum of 25 terms of an A.P.
\(-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } \) is

Question 19.
In an A.P., if a = 1, a_n = 20 and S_n = 399, then n is
(a) 19
(b) 21
(c) 38
(d) 42
Solution:
In an A.P., a = 1, a_n = 20, S_n = 399, n is ?
a_n = a + (n – 1 )d = 20
1 +(n – 1)d = 20
(n – 1)d = 20 – 1 = 19 …(i)

Question 20.
In an A.P., if a = – 5, l = 21. and S_n = 200, then n is equal to
(a) 50
(b) 40
(c) 32
(d) 25
Solution:
In an A.P.
a = -5, l = 21, S_n = 200, n = ?
l = a + (n – 1)d = -5 + (n – 1 )d
21 = -5 + (n – 1)d

Question 21.
In an A.P., if a = 3 and S₈ = 192, then d is
(a) 8
(b) 7
(c) 6
(d) 4
Solution:
In an A.P.
a = 3, S₈ =192, d = ?

Question 22.
The sum of first five multiples of 3 is
(a) 45
(b) 55
(c) 65
(d) 75
Solution:
First 5 multiples of 3 :
3, 6, 9, 12, 15
Here, a = 3, d = 6 – 3 = 3

Question 23.
The number of two digit numbers which are divisible by 3 is
(a) 33
(b) 31
(c) 30
(d) 29
Solution:
Two digit number which are divisible by 3 is 12, 15, 18, 21, … 99
Here, a = 12, d = 3, l = 99
l = a_n = a + (n – 1)d
⇒ 12 + (n – 1) x 3 = 99
⇒ (n – 1)3 = 99 – 12 = 87
⇒ n – 1 = \(\\ \frac { 87 }{ 3 } \) = 29
⇒ n = 29 + 1 = 30 (c)

Question 24.
The number of multiples of 4 that lie between 10 and 250 is
(a) 62
(b) 60
(c) 59
(d) 55
Solution:
Multiples of 4 lying between 10 and 250 12, 16, 20, 24, …, 248
Here, a = 12, d = 16 – 12 = 4, l = 248

Question 25.
The sum of first 10 even whole numbers is
(a) 110
(b) 90
(c) 55
(d) 45
Solution:
Sum of first 10 even whole numbers
Even numbers are 0, 2, 4, 6, 8, 10, 12, 14, 16, 18
Here, a = 0, d = 2, n = 10

Question 26.
The list of number \(\\ \frac { 1 }{ 9 } \) , \(\\ \frac { 1 }{ 3 } \), 1, – 3,… is a
(a) GP. with r = – 3
(b) G.P. with r = \(– \frac { 1 }{ 3 } \)
(c) GP. with r = 3
(d) not a G.P.
Solution:
The given list of numbers
\(\\ \frac { 1 }{ 9 } \) , \(\\ \frac { 1 }{ 3 } \), 1, – 3,…

Question 27.
The 11th of the G.P. \(\\ \frac { 1 }{ 8 } \) , \(– \frac { 1 }{ 4 } \) , 2, – 1, … is
(a) 64
(b) – 64
(c) 128
(d) – 128
Solution:
11th of the G.P.
\(\\ \frac { 1 }{ 8 } \) , \(– \frac { 1 }{ 4 } \) , 2, -1, … is

Question 28.
The 5th term from the end of the G.P. 2, 6, 18, …, 13122 is
(a) 162
(b) 486
(c) 54
(d) 1458
Solution:
5th term from the end of the G.P. 2, 6, 18, …, 13122 is
Here, a = 2, r = \(\\ \frac { 6 }{ 2 } \) = 3, l = 13122

Question 29.
If k, 2(k + 1), 3(k + 1) are three consecutive terms of a G.P., then the value of k is
(a) – 1
(b) – 4
(c) 1
(d) 4
Solution:
k, 2(k + 1), 3(k + 1) are in G.P.
[2(k + 1)]² = k x 3(k + 1)
⇒ 4(k + 1)² = 3k(k + 1)
⇒ 4 (k + 1) = 3 k
(Dividing by k + 1 if k + 1 ≠ 0) 4
⇒ 4k + 4 = 3k
⇒ 4k – 3k = -4
⇒ k = -4 (b)

Question 30.
Which term of the G.P. 18, – 12, 8, … is \(\\ \frac { 512 }{ 729 } \) ?
(a) 12th
(b) 11th
(c) 10th
(d) 9th
Solution:
Which term of the G.P.
18, -12, 8,… \(\\ \frac { 512 }{ 729 } \)
Let it be nth term

Question 31.
The sum of the first 8 terms of the series 1 + √3 + 3 + … is
Solution:
Sum of first 8 terms of 1 + √3 + 3 + … is
Here a = 1, \(r=\frac { \sqrt { 3 } }{ 1 } =\sqrt { 3 } \) , n = 8

Question 32.
The sum of first 6 terms of the G.P. 1, \(– \frac { 2 }{ 3 } \) ,\(\\ \frac { 4 }{ 9 } \) ,… is
(a) \(– \frac { 133 }{ 243 } \)
(b) \(\\ \frac { 133 }{ 243 } \)
(c) \(\\ \frac { 793 }{ 1215 } \)
(d) none of these
Solution:
Sum of first 6 terms of G.P.
1, \(– \frac { 2 }{ 3 } \) ,\(\\ \frac { 4 }{ 9 } \) ,…

Question 33.
If the sum of the GP., 1,4, 16, … is 341, then the number of terms in the GP. is
(a) 10
(b) 8
(c) 6
(d) 5
Solution:
The sum of G.P. 1, 4, 16, … is 341
Let n be the number of terms,

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
Find the values of a and below
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
Solution:
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
comparing the corresponding elements
a + 3 = 2a + 1
⇒ 2a – a =3 – 1
⇒ a = 2
b² + 2 = 3b
⇒ b² – 3b + 2 = 0
⇒ b² – b – 2b + 2 = 0
⇒ b (b – 1) – 2 (b – 1) = 0
⇒ (b – 1) (b – 2) = 0.
Either b – 1 = 0, then b = 1
or b – 2 = 0, then b = 2
Hence a = 2, b = 2 or 1

Question 2.
Find a, b, c and d if \(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)
Solution:
Given
\(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)

Question 3.
Find X if Y = \(\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \) and 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
Solution:
Given
2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
⇒ 2X = 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \) – Y

Question 4.
Determine the matrices A and B when
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) and 2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \)
Solution:
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) …..(i)
2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \) …….(ii)
Multiplying (i) by 1 and (ii) by 2

Question 5.
(i) Find the matrix B if A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \) and A² = A + 2B
(ii) If A = \(\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix} \), B = \(\begin{bmatrix} 0 & 1 \\ -2 & 5 \end{bmatrix} \)
and C = \(\begin{bmatrix} -2 & 0 \\ -1 & 1 \end{bmatrix} \) find A(4B – 3C)
Solution:
A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \)
let B = \(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \)

Question 6.
If A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \), B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \) compute (AB)C = (CB)A ?
Solution:
Given
A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \),
B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and
C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \)

Question 7.
If A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \) find the each of the following and state it they are equal:
(i) (A + B)(A – B)
(ii)A² – B²
Solution:
Given
A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and
B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)

Question 8.
If A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \) find A² – 5A – 14I
Where I is unit matrix of order 2 x 2
Solution:
Given
A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \)

Question 9.
If A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \) and A² = 0 find p and q
Solution:
Given
A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \) and A² = I, find x,y
Solution:
Given
A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \)

Question 11.
If \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \) find a,b,c and d
Solution:
Given
\(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \)

Question 12.
Find a and b if
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)
Solution:
Given
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)
Find (i) 2A – 3B (ii) A² (iii) BA
Solution:
Given
A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and
B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the sum of:
(i) 20 terms of the series 2 + 6 + 18 + …
(ii) 10 terms of series 1 + √3 + 3 + …
(iii) 6 terms of the GP. 1, \(– \frac { 2 }{ 3 } \) , \(\\ \frac { 4 }{ 9 } \), …
(iv) 20 terms of the GP. 0.15, 0.015, 0.0015,…
(v) 100 terms of the series 0.7 + 0.07 + 0.007 +…
(vi) 5 terms and n terms of the series \(1+\frac { 2 }{ 3 } +\frac { 4 }{ 9 } +…\)
(vii) n terms of the G.P. √7, √21, 3√7, …
(viii)n terms of the G.P. 1, – a, a², – a³, … (a ≠ – 1)
(ix) n terms of the G.P. x³, x⁵ , x⁷, … (x ≠ ±1).
Solution:
(i) 2 + 6 + 18 + … 20 terms
Here, a = 2, r = 3, n = 20, r > 1

Question 2.
Find the sum of the first 10 terms of the geometric series
√2 + √6 + √18 + ….
Solution:
√2 + √6 + √18 + ….
Here, a = √2 , r = √3, r > 1

Question 3.
Find the sum of the series 81 – 27 + 9….\(– \frac { 1 }{ 27 } \)
Solution:
Given
81 – 27 + 9….\(– \frac { 1 }{ 27 } \)

Question 4.
The nth term of a G.P. is 128 and the sum of its n terms is 255. If its common ratio is 2, then find its first term.
Solution:
In a G.P.
T_n =128
S_n = 255
r = 2,
Let a be the first term, then

Question 5.
If the sum of first six terms of any G.P. is equal to 9 times the sum of the first three terms, then find the common ratio of the G.P.
Solution:
Sum of first 6 terms of a G.P. = 9 x The of first 3 terms
Let a be the first term and r be the common ratio

Question 6.
A G.P. consists of an even number of terms. If the sum of all the terms is 3 times the sum of the odd terms, then find its common ratio.
Solution:
Let the G.P. be a, ar, ar², … ar^{2n – 1}
These are 2n in number, which is an even number
A.T.Q.

Question 7.
(i) How many terms of the G.P. 3, 3², 3³, … are needed to give the sum 120?
(ii) How many terms of the G.P. 1, 4, 16, … must be taken to have their sum equal to 341?
Solution:
In G.P.
(i) 3, 3², 3³, …
Sum = 120, Here, a = 3, r = \(\frac { { 3 }^{ 2 } }{ 3 } \) = 3, r > 1

Question 8.
How many terms of the GP. 1, √2 > 2, 2 √2 , … are required to give a sum of 1023( √2 + 1)?
Solution:
GP. 1, √2 > 2, 2 √2 , …
Sum = 1023 (√2 + 1)
Here, a = 1, r = √2 . r > 1
Let number of terms be n, then

Question 9.
How many terms of the \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\) will make the sum \(\\ \frac { 55 }{ 72 } \) ?
Solution:
G.P. is \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\)
sum \(\\ \frac { 55 }{ 72 } \)

Question 10.
The 2nd and 5th terms of a geometric series are \(– \frac { 1 }{ 2 } \) and sum \(\\ \frac { 1 }{ 16 } \) respectively. Find the sum of the series upto 8 terms.
Solution:
In a G.P.
a₂ = \(– \frac { 1 }{ 2 } \) and a₅ = \(\\ \frac { 1 }{ 16 } \)
Let a be the first term and r be the common ratio

Question 11.
The first term of a G.P. is 27 and 8th term is \(\\ \frac { 1 }{ 81 } \) . Find the sum of its first 10 terms.
Solution:
In a G.P.
First term (a) = 27
a₈ = 81
Let r be the common ratio, then

Question 12.
Find the first term of the G.P. whose common ratio is 3, last term is 486 and the sum of whose terms is 728
Solution:
Common ratio of a G.P. = 3
and last term = 486
and sum of terms = 728

Question 13.
In a G.P. the first term is 7, the last term is 448, and the sum is 889. Find the common ratio.
Solution:
In a GP.
First term (a) = 7, last term (l) = 448
and sum = 889
Let r be the common ratio, then

Question 14.
Find the third term of a G.P. whose common ratio is 3 and the sum of whose first seven terms is 2186.
Solution:
In a G.P.
Common ratio = 3

Question 15.
If the first term of a G.P. is 5 and the sum of first three terms is \(\\ \frac { 31 }{ 5 } \), find the common ratio.
Solution:
In a G.P.
First term (a) = 5

Question 16.
The sum of first three terms of a GP. is to the sum of first six terms as 125 : 152. Find the common ratio of the GP.
Solution:
S₃ ÷ S₆ = 125 : 152
Let r be the common ratio and a be the first number, then

Question 17.
Find the sum of the products of the corresponding terms of the geometric progression 2, 4, 8, 16, 32 and 128, 32, 8, 2, \(\\ \frac { 1 }{ 2 } \)
Solution:
Sum of the product of corresponding terms of the G.M.s

Question 18.
Evaluate \(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Solution:
\(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Here n = 1, 2, 3,….,50

Question 19.
Find the sum of n terms of a series whose mth term is 2^m + 2m.
Solution:
a_m = 2^m + 2m
a₁ = 2¹ + 2 x 1 = 2 + 2

Question 20.
Sum the series
x(x + y) + x² (x² + y²) + x³ (x³ + y³) … to n terms.
Solution:
Given
S_n = x(x + y) + x² (x² + y²) + x³ (x³ + y³) … n terms

Question 21.
Find the sum of the series
1 + (1 + x) + (1 + x + x²) + … to n terms, x ≠ 1.
Solution:
1 + (1 + x) + (1 + x + x²) +… n terms, x ≠ 1
Multiply and divide by (1 – x)

Question 22.
Find the sum of the following series to n terms:
(i) 7 + 77 + 777 + …
(ii) 8 + 88 + 888 + …
(iii) 0.5 + 0.55 + 0.555 + …
Solution:
(i) 7 + 77 + 777 + … n terms
= 7[1 + 11 + 111 + … n terms]

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test.

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
The point P (4, – 7) on reflection in x-axis is mapped onto P’. Then P’ on reflection in the y-axis is mapped onto P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of P (4, -7) reflected in x-axis
∴ Co-ordinates of P’ are (4, 7)
Again P” is the image of P’ reflected in y-axis
∴ Co-ordinates of P” are (-4, 7)
∴ Single transformation that maps P and P” is in the origin.

Question 2.
The point P (a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (3, – 4), evaluate a, b
Solution:
The co-ordinates of image of P(a, b) reflected in origin are (-a, -b).
Again the co-ordinates of P’, image of the above point (-a, -b)
reflected in the y-axis are (a, -b).
But co-ordinates of P’ are (3, -4)
∴a = 3 and -b = -4
b = 4 Hence a = 3, b = 4.

Question 3.
A point P (a, b) becomes ( – 2, c) after reflection in the x-axis, and P becomes (d, 5) after reflection in the origin. Find the values of a, b, c and d.
Solution:
If the image of P (a, b) after reflected in the x-axis be (a, -b) but it Is given (-2, c).
a = -2, c = -b
If P is reflected in the origin, then its co-ordinates will be (-a, -b), but it is given (d, 5)
∴ -b = 5 ⇒ b = -5
d = -a = -(-2) = 2, c = -b = -(-5) = 5
Hence a = -2, b = -5, c = 5, d = 2

Question 4.
A (4, – 1), B (0, 7) and C ( – 2, 5) are the vertices of a triangle. ∆ ABC is reflected in the y-axis and then reflected in the origin. Find the co-ordinates of the final images of the vertices.
Solution:
A (4, -1), B (0, 7) and C (-2, 5) are the vertices of ∆ABC.
After reflecting in y-axis, the co-ordinates of points will be
A’ (-4, -1), B’ (0, 7), C’ (2, 5). Again reflecting in origin,
the co-ordinates of the images of the vertices will be
A” (4, 1), B” (0, -7), C” (-2, -5)

Question 5.
The points A (4, – 11), B (5, 3), C (2, 15), and D (1, 1) are the vertices of a parallelogram. If the parallelogram is reflected in the y-axis and then in the origin, find the co-ordinates of the final images. Check whether it remains a parallelogram. Write down a single transformation that brings the above change.
Solution:
The points A (4, -11), B (5, 3), C (2, 15) and D (1, 1) are the vertices of a parallelogram.
After reflecting in/-axis, the images of these points will be
A’ ( -4, 11), B’ (-5, 3), C (-2, 15) and D’ (-1, 1).
Again reflecting these points in origin, the image of these points will be
A” (4, -11), B” (5, -3), C” (2, -15), D” (0, -1)
Yes, the reflection of a single transformation is in the x-axis.

Question 6.
Use a graph paper for this question (take 2 cm = 1 unit on both x and y axes).
(i) Plot the following points:
A (0, 4), B (2, 3), C (1, 1) and D (2, 0).
(ii) Reflect points B, C, D on 7-axis and write down their coordinates. Name the images as B’, C’, D’ respectively.
(iii) Join points A, B, C, D, D’, C’, B’ and A in order, so as to form a closed figure. Write down the equation of line of symmetry of the figure formed. (2017)
Solution:
(i) On graph A (0, 4), B (2, 3), C (1, 1) and D (2, 0)
(ii) B’ = (-2, 3), C’ = (-1, 1), D’ = (-2, 0)

The equation of the line of symmetry is x = 0

Question 7.
The triangle OAB is reflected in the origin O to triangle OA’B’. A’ and B’ have coordinates ( – 3, – 4) and (0, – 5) respectively.
(i) Find the co-ordinates of A and B.
(ii) Draw a diagram to represent the given information.
(iii) What kind of figure is the quadrilateral ABA’B’?
(iv) Find the coordinates of A”, the reflection of A in the origin followed by reflection in the y-axis.
(v) Find the co-ordinates of B”, the reflection of B in the x-axis followed by reflection in the origin.
Solution:
∆ OAB is reflected in the origin O to ∆ OA’B’,
Co-ordinates of A’ = (-3, -4), B’ (0, -5).
.’. Co-ordinates of A will be (3, 4) and of B will be (0, 5).
(ii) The diagram representing the given information has been drawn here.
(iii) The figure in the diagram is a rectangle.
(iv) The co-ordinates of B’, the reflection of B is the x-axis is (0, -5)
and co-ordinates of B”, the reflection in origin of the point (0, -5) will be (0, 5).
(v) The co-ordinates of the points, the reflection of A in the origin are (-3, -4)
and coordinates of A”, the reflected in y-axis of the point (-3, – 4) are (3, -4)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Choose the correct answer from the given four options (1 to 14) :

Question 1.
If A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
(a) \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)
(b) \(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix} \)
Solution:
A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
\(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \) (b)

Question 2.
If \(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 7
(b) x = 7, y = 2
(c) x = 3, y = 6
(d) x = – 2, y = 7
Solution:
\(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing we get
x + 3 = 5
⇒ x = 5 – 3 = 2
and y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7 (a)

Question 3.
If \(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 3
(b) x = 2, y = – 3
(c) x = – 2, y = 3
(d) x = 3, y = 2
Solution:
\(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \)
Comparing, we get
3x = 6
⇒ \(x= \frac { 6 }{ 3 } \) = 2
⇒ -y = 3
⇒ y = – 3
x = 2, y = -3 (b)

Question 4.
If \(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \) then the value of x is
(a) – 2
(b) 0
(c) 1
(d) 2
Solution:
\(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \)
Comparing, we get
y = -2
and x – 2y = 6
⇒ x – 2 x (-2) = 6
⇒ x + 4 = 6
⇒ x = 6 – 4 = 2 (d)

Question 5.
If \(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \) then the value of x – y is
(a) – 3
(b) 1
(c) 3
(d) 5
Solution:
\(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \)
Comparing, we get
3y = -3
⇒ \(y= \frac { -3 }{ 3 } \) = -1
4x = 8
⇒ \(x= \frac { 8 }{ 4 } \) = 2
x – y = 2 – (-1) = 2 + 1 = 3 (c)

Question 6.
If \(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \) then the values of x and y are
(a) x = 2, y = 6
(b) x = 2, y = – 6
(c) x = 3, y = – 4
(d) x = 3, y = – 6
Solution:
Given
\(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \)

Question 7.
If B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)
then the matrix A is equal to
(a) \(\begin{bmatrix} 2 & 14 \\ -7 & 11 \end{bmatrix} \)
(b) \(\begin{bmatrix} -2 & 14 \\ 7 & 11 \end{bmatrix} \)
(c) \(\begin{bmatrix} 2 & -14 \\ 7 & 11 \end{bmatrix} \)
(d) \(\begin{bmatrix} -2 & 14 \\ -7 & 11 \end{bmatrix} \)
Solution:
Given
B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)

Question 8.
If A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)
then A is equal to
(a) \(\frac { 1 }{ 3 } \begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(b) \(\frac { 1 }{ 3 } \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
Solution:
A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)

Question 9.
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \) then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)

Question 11.
If A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) A
(b) O
(c) I
(d) 2A
Solution:
Given
A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \)

Question 12.
If A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 2 & 0 \\ 1 & 1 \end{bmatrix} \)
(b) \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix} \)
(d) none of these
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix} \)
(b) \(\begin{bmatrix} 8 & -5 \\ 5 & 3 \end{bmatrix} \)
(c) \(\begin{bmatrix} 8 & -5 \\ -5 & -3 \end{bmatrix} \)
(d) \(\begin{bmatrix} 8 & -5 \\ -5 & 3 \end{bmatrix} \)
Solution:
A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)
A² = A x A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)\(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)

Question 14.
If A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \) , then A² = pA, then the value of p is
(a) 2
(b) 4
(c) – 2
(d) – 4
Solution:
A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \)
and A² = pA

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Choose the correct answer from the given four options (1 to 7) :

Question 1.
The reflection of the point P ( – 2, 3) in the x-axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) ( – 2, 3)
Solution:
Reflection of the point P (-2, 3) in x-axis is (-2, -3) (c)

Question 2.
The reflection of the point P ( – 2, 3) in the y- axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) (0, 3)
Solution:
The reflection of the point P (-2, 3) under reflection in y-axis (2, 3) (a)

Question 3.
If the image of the point P under reflection in the x-axis is ( – 3, 2), then the coordinates of the point P are
(a) (3, 2)
(b) ( – 3, – 2)
(c) (3, – 2)
(d) ( – 3, 0)
Solution:
The image of the point P under reflection in the x-axis is (-3, 2),
then the co-ordinates of the point P will be (-3, -2) (b)

Question 4.
The reflection of the point P (1, – 2) in the line y = – 1 is
(a) ( – 3, – 2)
(b) (1, – 4)
(c) (1 , 4)
(d) (1, 0)
Solution:
The reflection of the point P (1, -2) in the line y = -1 is (1, 0) (d)

Question 5.
The reflection of the point A (4, -1) in the line x = 2 is
(a) (0, – 1)
(b) (8, – 1)
(c) (0, 1)
(d) none of these
Solution:
The reflection of A (4, -1) in the line x = 2 will be A’ (0, -1) (a)

Question 6.
The reflection of the point ( – 3, 0) in the origin is the point
(a) (0, – 3)
(b) (0, 3)
(c) (3, 0)
(d) none of these
Solution:
Reflection of the point (-3, 0) in origin will be (3, 0) (c)

Question 7.
Which of the following points is invariant with respect to the line y = – 2 ?
(a) (3, 2)
(b) (3, – 2)
(c) (2, 3)
(d) ( – 2, 3)
Solution:
The variant points are (3, -2) (b)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Can 0 be a term of a geometric progression?
Solution:
No, 0 is not a term of geometric progression.

Question 2.
(i) Find the next term of the list of numbers \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)
(ii) Find the next term of the list of numbers \(\frac { 3 }{ 16 } ,-\frac { 3 }{ 8 } ,\frac { 3 }{ 4 } ,-\frac { 3 }{ 2 } ,…\)
(iii) Find the 15th term of the series \(\sqrt { 3 } +\frac { 1 }{ \sqrt { 3 } } +\frac { 1 }{ 3\sqrt { 3 } } +…\)
(iv) Find the nth term of the list of numbers \(\frac { 1 }{ \sqrt { 2 } } ,-2,4\sqrt { 2 } ,-16,…\)
(v) Find the 10th and nth terms of the list of numbers 5, 25, 125, …
(vi) Find the 6th and the nth terms of the list of numbers \(\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } ,\frac { 3 }{ 8 } ,…\)
(vii) Find the 6th term from the end of the list of numbers 3, – 6, 12, – 24, …, 12288.
Solution:
(i) Given
⇒ \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)

Question 3.
Which term of the G.P.
(i) 2, 2√2, 4, … is 128?
(ii) \(1,\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,…is\quad \frac { 1 }{ 243 } ?\)
(iii) \(\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 27 } ,…is\quad \frac { 1 }{ 19683 } ? \)
Solution:
Given
(i) 2, 2√2, 4, … is 128?
Here a = 2, \(r=\frac { 2\sqrt { 2 } }{ 2 } =\sqrt { 2 } \), l = 128

Question 4.
Which term of the G.P. 3, – 3√3, 9, – 9√3, … is 729 ?
Solution:
G.P. 3, -3√3, 9, – 9√3, … is 729 ?
Here a = 3, \(r=\frac { -3\sqrt { 3 } }{ 3 } =\sqrt { -3 } \), l = 729

Question 5.
Determine the 12th term of a G.P. whose 8th term is 192 and common ratio is 2.
Solution:
In a G.P.
a₈ = 192 and r = 2
Let a be the first term and r be the common ratio then.

∴ a₁₂ = 3072

Question 6.
In a GP., the third term is 24 and 6th term is 192. Find the 10th term
Solution:
In a GP.
a₃ = 24 and a₆ = 192, a₁₀ = ?
Let a be the first term and r be the common ratio, therefore

Question 7.
Find the number of terms of a G.P. whose first term is \(\\ \frac { 3 }{ 4 } \), common ratio is 2 and the last term is 384.
Solution:
First term of a G.P. (a) = \(\\ \frac { 3 }{ 4 } \)
and common ratio (r) = 2
Last term = 384
Let number of terms is n

Question 8.
Find the value of x such that
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.
(ii) x + 9, x – 6 and 4 are three consecutive terms of a G.P.
(iii) x, x + 3, x + 9 are first three terms of a G.P. Sol. Find the value of x
Solution:
Find the value of x
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.

Question 9.
If the fourth, seventh and tenth terms of a G.P. are x, y, z respectively, prove that x, y, z are in G.P.
Solution:
In a G.P.
a₄ = x, a₇ = y, a₁₀ = z
To prove : x, y, z are in G.P.
Let a be the first term and r be the common

Question 10.
The 5th, 8th and 11th terms of a G.P. are p, q and s respectively. Show that q² = ps.
Solution:
In a G.P.
a₅ = p, a₈ = q and a₁₁ = s
To show that q² = px
Let a be the first term and r be the common

Question 11.
If a, b, c are in G.P., then show that a², b², c² are also in G.P.
Solution:
a, b, c are in G.P.
Show that a², b², c² are also in G.P
∵ a, b, c are in G.P., then
b² = ac …(i)
a², b², c² will be in G.P.
if (b²)² = a² x c²
⇒ (ac)² = a²c² [From (i)]
⇒ a²c² = a²c² which is true.
Hence proved.

Question 12.
If a, b, c are in A.P., then show that 3^a, 3^b, 3^c are in G.P.
Solution:
a, b and c are in A.P.
Then, 2b = a + c
Now, 3^a, 3^b, 3^c will be in G.P.
if (3^b)² = 3^a.3^c
if 3^2b = 3^a+c
Comparing, we get
if 2b = a + c
Which are in A.P. is given

Question 13.
If a, b, c are in A.P., then show that 10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0, are in G.P.
Solution:
a, b, c are in A.P.
To show that are in G.P.10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0
∵ a, b, c are in A.P.

Question 14.
If a, a²+ 2 and a³ + 10 are in G.P., then find the values(s) of a.
Solution:
a, a² + 2 and a³ + 10 are in G.P.
∵ (a² + 2)² = a(a³ + 10)

Question 15.
If k, 2k + 2, 3k + 3, … are in G.P., then find the common ratio of the G.P.
Solution:
k, 2k + 2, 3k + 3, … are in G.P.
then, (2k + 2)² = k(3k + 3)
⇒ 4k² + 8k + 4 = 3k² + 3k
⇒ 4k² + 8k + 4 – 3k² – 3k = 0

Question 16.
The first and the second terms of a GP. are x^-4 and x^m . If its 8th term is x⁵², then find the value of m.
Solution:
In a G.P.,
First term (a₁) = x^-4 …(i)
Second term (a₂) = x^m
Eighth term (a₈) = x⁵²

Question 17.
Find the geometric progression whose 4th term is 54 and the 7th Term is 1458.
Solution:
In a G.P.,
4th term (a₄) = 54

Question 18.
The fourth term of a GP. is the square of its second term and the first term is – 3. Determine its seventh term.
Solution:
In a GP.
a_n is square of a₂ i.e. an = (a₂)²
a₁ = – 3

Question 19.
The sum of first three terms of a G.P. is \(\\ \frac { 39 }{ 10 } \) and their product is 1. Find the common ratio and the terms.
Solution:
Sum of first three terms of G.P. = \(\\ \frac { 39 }{ 10 } \)
and their product = 1

Question 20.
Three numbers are in A.P. and their sum is 15. If 1, 4 and 19 are added to these numbers respectively, the resulting numbers are in G.P. Find the numbers.
Solution:
Given: Three numbers are in A.P. and their sum = 15
Let a – d, a, a + d be the three number in A.P.

Question 21.
Three numbers form an increasing G.P. If the middle term is doubled, then the new numbers are in A.P. Find the common ratio of the G.P.
Solution:
Three numbers form an increasing G.P.
Let \(\\ \frac { a }{ r } \) ,a,ar be three numbers in G.P.
Double the middle term, we get

Question 22.
Three numbers whose sum is 70 are in GP. If each of the extremes is multiplied by 4 and the mean by 5, the numbers will be in A.P. Find the numbers.
Solution:
Three numbers are in G.P.
Let numbers be
\(\\ \frac { r }{ a } \), a, ar

Question 23.
There are four numbers such that first three of them form an A.P. and the last three form a GP. The sum of the first and third number is 2 and that of second and fourth is 26. What are these numbers?
Solution:
There are 4 numbers, such that
First 3 numbers are in A.P. and
last 3 numbers are in GP.
Sum of first and third numbers = 2
and sum of 2nd and 4th = 26

Question 24.
(i) If a, b, c are in A.P. as well in G.P., prove that a = b = c.
(ii) If a, b, c are in A.P as well as in G.P., then find the value of a^b-c + b^c-a + c^a-b
Solution:
(i) a, b, c are in A.P. as well as in GP.
To prove: a = b = c
a, b, c are in A.P.

Question 25.
The terms of a G.P. with first term a and common ratio r are squared. Prove that resulting numbers form a G.P. Find its first term, common ratio and the nth term.
Solution:
In a G.P.,
The first term = a
and common ratio = r
GP. is a, ar, ar²
Squaring we get

Question 26.
Show that the products of the corresponding terms of two G.P.’s a, ar, ar², …, ar^n-1 and A, AR, AR², …, AR^n-1 form a G.P. and find the common ratio.
Solution:
It has to be proved that the sequence
aA, arAR, ar²AR², …, ar^n-1AR^n-1 and forms a G.P.

Question 27.
(i) If a, b, c are in G.P. show that \(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) are also in G.P.
(ii) If K is any positive real number and K^a, K^b K^c are three consecutive terms of a G.P., prove that a, b, c are three consecutive terms of an A.P.
(iii) If p, q, r are in A.P., show that pth, qth and rth terms of any G.P. are themselves in GP.
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
\(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) will be in G.P.

Question 28.
If a, b, c are in GP., prove that the following are also in G.P.
(i) a³, b³, c³
(ii) a² + b², ab + bc, b² + c².
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
a³, b³, c³ are in G.P.

Question 29.
If a, b, c, d are in G.P., show that
(i) a² + b², b² + c², c² + d² are in G.P.
(ii) (b – c)² + (c – a)² + (d – b)² = (a – d)².
Solution:
a, b, c, d are in G.P.
Let r be the common ratio, then a = a
b = ar, c = ar², d = ar³

Question 30.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
Solution:
Bacteria in the beginning = 30 = a
After every hours, it doubles itself
After 1 hour it becomes = 30 x 2 = 60 = ar
After 2 hours it will becomes = 60 x 2 = 120 = a²
After 3 hours, it will becomes = 120 x 2 = 240 = a³
After 4 hours it will becomes = 240 x 2 = 480 = a⁴
∴ After n hour, it will become = arⁿ

Question 31.
The length of the sides of a triangle form a G.P. If the perimeter of the triangle is 37 cm and the shortest side is of length 9 cm, find the lengths of the other two sides.
Solution:
Lengths of a triangle are in GP. and its sum is 37 cm
Let sides be a, ar, ar²
a + ar + ar² = 37
a = 9

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
Find the co-ordinates of the images of the following points under reflection in the x- axis:
(i) (2, -5)
(ii) \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \)
(iii) ( – 7, 0)
Solution:
Co-ordinates of the images of the points
under reflection in the x-axis will be
(i) Image of (2, -5) will be (2, 5)
(ii) Image of \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \) will be \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of ( -7, 0) will be (-7, 0)

Question 2.
Find the co-ordinates of the images of the following points under reflection in the y-axis:
(i) (2, – 5)
(ii) \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) (0, – 7)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be ( -2, -5)
(ii) Image of \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, -7) will be (0, -7)

Question 3.
Find the co-ordinates of the images of the following points under reflection in the origin:
(i) (2, – 5)
(ii) \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \)
(iii) (0, 0)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be (-2, 5)
(ii) Image of \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, 0) will be (0, 0)

Question 4.
The image of a point P under reflection in the x-axis is (5, – 2). Write down the co-ordinates of P.
Solution:
As the image of a point (5, -2) under x – axis is P
∴ Co-ordinates of P will be (5, 2)

Question 5.
A point P is reflected in the x-axis. Co-ordinates of its image are (8, – 6).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
The co-ordinates of image of P which is reflected in x-axis are (8, – 6), then
(0 Co-ordinates of P will be (8, 6)
(ii) Co-ordinates of image of P under reflection in the y-axis will be ( – 8, 6)

Question 6.
A point P is reflected in the origin. Co-ordinates of its image are (2, – 5). Find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P in the x-axis.
Solution:
The co-ordinates of image of a point P which is reflected in origin are (2, – 5), then
(i) Co-ordinates of P will be ( – 2, 5)
(ii) Co-ordinates of the image of P in the x- axis will be ( – 2, – 5)

Question 7.
(i) The point P (2, 3) is reflected in the line x = 4 to the point P’. Find the co-ordinates of the point P’.
(ii) Find the image of the point P (1, – 2) in the line x = – 1.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit
(b) Plot point P (2, 3) on it.
(c) Draw a line x = 4 which is parallel to y-axis.
(d) From P, draw a perpendicular on x = 4, which intersects x = 4 at Q.
(e) Produce PQ to P’, such that QP’ = QP.
∴ P’ is the reflection of P in the line x = 4
Co-ordinates of P’ are (6, 3)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot the point P (1, -2) on it.
(c) Draw a line x = -1 which is parallel toy-axis.
(d) From P, draw a perpendicular on the line x = -1, which meets it at Q.
(e) Produce PQ to P’ such that PQ = QP’
P’ is the image or reflection of P in the line x = -1
Co-ordinates of P’ are (-3, -2)
Co-ordinates of P’ are (-3, -2)

Question 8.
(i) The point P (2, 4) on reflection in the line y = 1 is mapped onto P’ Find the co-ordinates of P’.
(ii) Find the image of the point P ( – 3, – 5) in the line y = – 2.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (2, 4) on it.
(c) Draw a line y = 1, which is parallel to x-axis.
(d) From P, draw a perpendicular on y = 1 meeting it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
P’ is the reflection of P whose co-ordinates are (2, -2)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (-3, -5) on it.
(c) Draw a line y = -2 which is parallel to the x-axis.
(d) From P, draw a perpendicular on y = -2 which meets it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
Then P’ is the image of P, whose co-ordinates are (-3, 1).

Question 9.
The point P ( – 4, – 5) on reflection in y-axis is mapped on P’. The point P’ on reflection in the origin is mapped on P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of point P (-4, -5) in y-axis
∴Co-ordinates of P’ will be (4, -5)
Again P” is the image of P’ under reflection in origin will be (-4, 5).
The single transformation that maps P onto P” is the x-axis

Question 10.
Write down the co-ordinates of the image of the point (3, – 2) when :
(i) reflected in the x-axis
(ii) reflected in the y-axis
(iii) reflected in the x-axis followed by reflection in the y-axis
(iv) reflected in the origin. (2000)
Solution:
Co-ordinates of the given points are (3, -2).
(i) Co-ordinates of the image reflected in x- axis will be (3, 2)
(ii) Co-ordinates of the image reflected in y- axis will be (-3, -2)
(iii) Co-ordinates of the point reflected in x- axis followed by reflection in the y-axis will be (-3, 2)
(iv) Co-ordinates of the point reflected in the origin will be (-3, 2)

Question 11.
Find the co-ordinates of the image of (3, 1) under reflection in x-axis followed by a reflection in the line x = 1.
Solution:
(i) Draw axis XOX’ and YOY’ taking 1 cm = 1 unit.
(ii) Plot a point P (3, 1).
(iii) Draw a line x = 1, which is parallel to y-axis.
(iv) From P, draw a perpendicular on x-axis meeting it at Q.
(v) Produce PQ to P’ such that QP’ = PQ, then
P’ is the image of P is x-axis. Then co-ordinates of P’ will be (3, -1)
(vi) From P’, draw a perpendicular on x = 1 meeting it at R.
(vii) Produce P’R to P” such that RP” = P’R
∴P” is the image of P’ in the line x = 1
Co-ordinates of P” are (-1, -1)

Question 12.
If P’ ( – 4, – 3) is the image of a point P under reflection in the origin, find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P under reflection in the line y = – 2.
Solution:
(i) Reflection of P is P’ (-4, -3) in the origin
∴ Co-ordinates of P will be (4, 3)
Draw a line y = -2, which is parallel to x-axis
(ii) From P, draw a perpendicular on y = -2 meetings it at Q
Produce PQ to P” such that QP” = PQ
∴P” will the image of P in the line y = -2
∴Co-ordinates of P” will be (4, -7)

Question 13.
A Point P (a, b) is reflected in the x-axis to P’ (2, – 3), write down the values of a and b. P” is the image of P, when reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line parallel to y-axis such that x = 4. (1998)
Solution:
P’ (2, -3) is the reflection of P (a, b) in the x-axis
∴Co-ordinates of P’ will be P’ (a, – b) but P’ is (2, -3)
Comparing a = 2, b = 3

∴Co-ordinates of P will be (2, 3)
P” is the image of P when reflected in y-axis
∴Co-ordinate of P” will be ( – 2, 3)
Draw a line x = 4, which is parallel to y-axis
and P'” is the image of P when it is reflected in the line x = 4,
then P'” is its reflection Co-ordinates of P”‘ will be (6, 3).

Question 14.
(i) Point P (a, b) is reflected in the x-axis to P’ (5, – 2). Write down the values of a and b.
(ii) P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”. (1997)
Solution:
(i) Image of P (a, b) reflected in the x-axis to P’ (5, -2)
∴ a = 5 and b = 2
(ii) P” is the image of P when reflected in the y-axis
∴ its co-ordinates will be (-5, -2).
(iii) The single transformation that maps P’ to P” is the origin.

Question 15.
Points A and B have co-ordinates (2, 5) and (0, 3). Find
(i) the image A’ of A under reflection in the x-axis.
(ii) the image B’ of B under reflection in the line AA’.
Solution:
Co-ordinates of A are (2, 5) and of B are (0, 3)

(i) Co-ordinates of A’, the image of A reflected in the x-axis will be (2, -5)
(ii) Co-ordinates of B’, the image of B under reflection in the line AA’ will be (4, 3).

Question 16.
Plot the points A (2, – 3), B ( – 1, 2) and C (0, – 2) on the graph paper. Draw the triangle formed by reflecting these points in the x-axis. Are the two triangles congruent?

Solution:
The points A (2, -3), B (-1, 2) and C(0, -2) has been plotted on the graph paper as shown and are joined to form a triangle ABC. The co-ordinates of the images of A, B and C reflected in x-axis will be A’ (2, 3), B’ (-1, -2), C’ (0, 2) respectively and are joined to from another ∆ A’B’C’
Yes, these two triangles are congruent.

Question 17.
The points (6, 2), (3, – 1) and ( – 2, 4) are the vertices of a right angled triangle. Check whether it remains a right angled triangle after reflection in the y-axis.
Solution:
Let A (6, 2), B (3, -1) and C (-2, 4) be the points of a right-angled triangle
then the co-ordinates of the images of A, B, C reflected in y-axis be
A’ (-6, 2), B’ (-3, -1) and C’ (2, 4).

By joining these points, we find that ∆A’B’C’ is also a right angled triangle.

Question 18.
The triangle ABC where A (1, 2), B (4, 8), C (6, 8) is reflected in the x-axis to triangle A’ B’ C’. The triangle A’ B’ C’ is then reflected in.the origin to triangle A”B”C” Write down the co-ordinates of A”, B”, C”. Write down a single transformation that maps ABC onto A” B” C”.
Solution:
The co-ordinates of ∆ ABC are A (1, 2) B (4, 8), C (6, 8)
which are reflected in x- axis as A’, B’ and C’.
∴ The co-ordinates of A’ (1, -2), B (4, -8) and C (6, -8).
A’, B’ and C’ are again reflected in origins to form an ∆A”B”C”.
∴ The co-ordinates of A” will be (-1, 2), B” (-4, 8) and C” (-6, 8)
The single transformation that maps ABC onto A” B” C” is y-axis.

Question 19.
The image of a point P on reflection in a line l is point P’. Describe the location of the line l.
Solution:
The line will be the right bisector of the line segment joining P and P’.

Question 20.
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate
(i) the x-axis
(ii) the y-axis and
(iii) the origin.
Solution:
Q is the image of P on reflection in y-axis
and mid point of PQ is invariant on reflection in x-axis

(i) x-axis will be the line joining the points P and Q.
(ii) The line perpendicular bisector of line segment PQ is the y-axis.
(iii) The origin will be the mid point of line segment PQ.

Question 21.
The point ( – 3, 0) on reflection in a line is mapped as (3, 0) and the point (2, – 3) on reflection in the same line is mapped as ( – 2, – 3).
(i) Name the mirror line.
(ii) Write the co-ordinates of the image of ( – 3, – 4) in the mirror line.
Solution:
The point (-3,0) is the image of point (3, 0)
and point (2, -3) is image of point (-2, -3) reflected on the same line.
(i) It is clear that the mirror line will be y-axis.
(ii) The co-ordinates of the image of the point (-3, -4)
reflected in the same line i.e. y-axis will be (3, -4).

Question 22.
A ( – 2, 4) and B ( – 4, 2) are reflected in the y-axis. If A’ and B’ are images of A and B respectively, find

(i) the co-ordinates of A’ and B’.
(ii) Assign special name to quad. AA’B’B.
(iii) State whether AB’ = BA’.
Solution:
A (-2, 4) and B (-4, 2) are reflected in y- axis as A’ and B’.

(i) Co-ordinates of A’ are (2, 4) and of B are (4, 2).
(ii) The quadrilateral AA’ B’ B is an isosceles trapezium.
(iii) yes, AB’ = BA’

Question 23.
Use graph paper for this question.
(i) The point P (2, – 4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(ii) Point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR. (2007)
Solution:
(i) Since the point Q is the reflection of the point P (2, -4) in the line x = 0,
the co-ordinates of Q are (2, 4).
(ii) Since R is the reflection of Q (2, 4) about the line y = 0,
the co-ordinates of R are ( – 2, 4).
(iii) Figure PQR is the right angled triangle PQR.

(iv) Area of ∆ PQR = \(\\ \frac { 1 }{ 2 } \) x QR x PQ
= \(\\ \frac { 1 }{ 2 } \) x 4 x 8
= 16 sq. units.

Question 24.
Use graph paper for this question. The point P (5, 3) was reflected in the origin to get the image P’.
(i) Write down the co-ordinates of P’.
(ii) If M is the foot of perpendicular from P to the x-axis, find the co-ordinates of M.
(iii) If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(iv) Name the figure PMP’N.
(v) Find the area of the figure PMP’N. (2001)
Solution:
P’ is the image of point P (5, 3) reflected in the origin.

(i) Co-ordinates of P’ will be (-5, -3).
(ii) M is the foot of the perpendicular from P to the x-axis.
Co-ordinates of M will be (5, 0)
(iii) N is the foot of the perpendicular from P’ to x-axis.
Co-ordinates of N will be (-5, 0).
(iv) By joining the points, the figure PMP’N is a parallelogram.
(v) Area of the parallelogram = 2 x area of ∆ MPN
= 2 x \(\\ \frac { 1 }{ 2 } \) x MN x PM = MN x PM
= 10 x 3 = 30 sq. units. Ans.

Question 25.
Using a graph paper, plot the points A (6, 4) and B (0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’B’.
(iv) Find its perimeter.
Solution:
(i) A (6, 4), B (0, 4)

Perimeter = Sum of all sides = 6 + 10 + 6 + 10 = 32 units

Question 26.
Use graph paper to answer this question
(i) Plot the points A (4, 6) and B (1, 2).
(ii) If A’ is the image of A when reflected in x-axis, write the co-ordinates of A’.
(iii) If B’ is the image of B when B is reflected in the line AA’, write the co-ordinates of B’.
(iv) Give the geometrical name for the figure ABA’B’. (2009)
Solution:
(i) Plotting the points A (4, 6) and B (1, 2) on the given graph.
(ii) A’ = (4, -6)
(iii) B’ = (7, 2)
(iv) In the quadrilateral ABA’B’, we have AB = AB’ and A’B = A’B’
Hence, ABA’B’ is a kite.

Question 27.
The points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ABC. (2006)
(i) Write down the co-ordinates of A1, B1, C1 if ∆ A1B1C1 is the image of ∆ ABC when reflected in the origin.
(ii) Write down the co-ordinates of A2, B2, C2 if ∆ A2B2C2 is the image of ∆ ABC when reflected in the x-axis.
(iii) Assign the special name to the quadrilateral BCC2B2 and find its area.


Solution:
Points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ ABC.
A1, B1 and C1 are the images of A, B and C reflected in the origin.
(i) Co-ordinates of A1 = (-2, -3) of B1 (-4, -5) and of C1 (-7, -2).
(ii) Co-ordinates of A2, B2 and C2 the images of A, B and C
when reflected in x-axis are A2 (2, – 3), B2 (4, – 5), C2 (7, – 2)
(iii) The quadrilateral formed by joining the points,
BCC2B2 is an isosceles trapezium and its area

Question 28.
The point P (3, 4) is reflected to P’ in the x-axis and O’ is the image of O (origin) in the line PP’. Find :
(i) the co-ordinates of P’ and O’,
(ii) the length of segments PP’ and OO’.
(iii) the perimeter of the quadrilateral POP’O’.
Solution:
P’ is the image of P (3, 4) reflected in x- axis
and O’ is the image of O the origin in the line P’P.
(i) Co-ordinates of P’ are (3, -4)
and co-ordinates of O’ reflected in PP’ are (6, 0)
(ii) Length of PP’ = 8 units and OO’ = 6 units
(iii) Perimeter of POP’O’ is

Question 29.
Use a graph paper for this question. (Take 10 small divisions = 1 unit on both axes). P and Q have co-ordinates (0, 5) and ( – 2, 4).
(i) P is invariant when reflected in an axis. Name the axis.
(ii) Find the image of Q on reflection in the axis found in (i).
(iii) (0, k) on reflection in the origin is invariant. Write the value of k.
(iv) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis. (2005)
Solution:

(i) Two points P (0, 5) and Q (-2, 4) are given As the abscissa of P is 0.
It is invariant when is reflected in y-axis.
(ii) Let Q’ be the image of Q on reflection in y-axis.
Co-ordinate of Q’ will be (2, 4)
(iii) (0, k) on reflection in the origin is invariant.
co-ordinates of image will be (0, 0). k = 0
(iv) The reflection of Q in the origin is the point Q”
and its co-ordinates will be (2, – 4)
and reflection of Q” (2, – 4) in x-axis is (2, 4) which is the point Q’

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.