ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
Find the co-ordinates of the images of the following points under reflection in the x- axis:
(i) (2, -5)
(ii) \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \)
(iii) ( – 7, 0)
Solution:
Co-ordinates of the images of the points
under reflection in the x-axis will be
(i) Image of (2, -5) will be (2, 5)
(ii) Image of \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \) will be \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of ( -7, 0) will be (-7, 0)

Question 2.
Find the co-ordinates of the images of the following points under reflection in the y-axis:
(i) (2, – 5)
(ii) \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) (0, – 7)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be ( -2, -5)
(ii) Image of \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, -7) will be (0, -7)

Question 3.
Find the co-ordinates of the images of the following points under reflection in the origin:
(i) (2, – 5)
(ii) \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \)
(iii) (0, 0)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be (-2, 5)
(ii) Image of \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, 0) will be (0, 0)

Question 4.
The image of a point P under reflection in the x-axis is (5, – 2). Write down the co-ordinates of P.
Solution:
As the image of a point (5, -2) under x – axis is P
∴ Co-ordinates of P will be (5, 2)

Question 5.
A point P is reflected in the x-axis. Co-ordinates of its image are (8, – 6).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
The co-ordinates of image of P which is reflected in x-axis are (8, – 6), then
(0 Co-ordinates of P will be (8, 6)
(ii) Co-ordinates of image of P under reflection in the y-axis will be ( – 8, 6)

Question 6.
A point P is reflected in the origin. Co-ordinates of its image are (2, – 5). Find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P in the x-axis.
Solution:
The co-ordinates of image of a point P which is reflected in origin are (2, – 5), then
(i) Co-ordinates of P will be ( – 2, 5)
(ii) Co-ordinates of the image of P in the x- axis will be ( – 2, – 5)

Question 7.
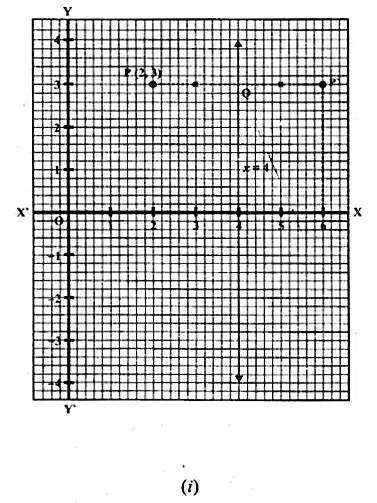
(i) The point P (2, 3) is reflected in the line x = 4 to the point P’. Find the co-ordinates of the point P’.
(ii) Find the image of the point P (1, – 2) in the line x = – 1.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit
(b) Plot point P (2, 3) on it.
(c) Draw a line x = 4 which is parallel to y-axis.
(d) From P, draw a perpendicular on x = 4, which intersects x = 4 at Q.
(e) Produce PQ to P’, such that QP’ = QP.
∴ P’ is the reflection of P in the line x = 4
Co-ordinates of P’ are (6, 3)

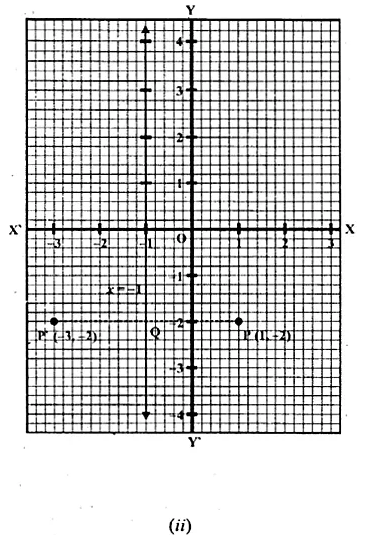
(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot the point P (1, -2) on it.
(c) Draw a line x = -1 which is parallel toy-axis.
(d) From P, draw a perpendicular on the line x = -1, which meets it at Q.
(e) Produce PQ to P’ such that PQ = QP’
P’ is the image or reflection of P in the line x = -1
Co-ordinates of P’ are (-3, -2)
Co-ordinates of P’ are (-3, -2)

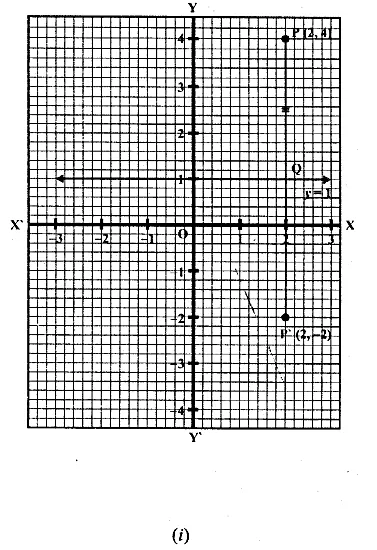
Question 8.
(i) The point P (2, 4) on reflection in the line y = 1 is mapped onto P’ Find the co-ordinates of P’.
(ii) Find the image of the point P ( – 3, – 5) in the line y = – 2.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (2, 4) on it.
(c) Draw a line y = 1, which is parallel to x-axis.
(d) From P, draw a perpendicular on y = 1 meeting it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
P’ is the reflection of P whose co-ordinates are (2, -2)

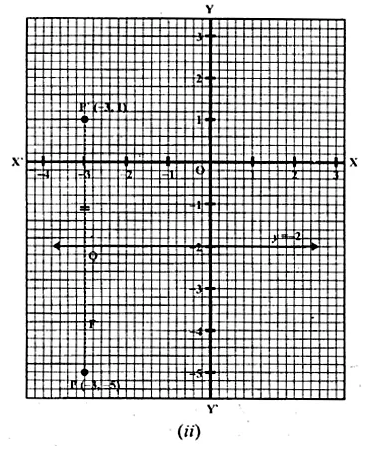
(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (-3, -5) on it.
(c) Draw a line y = -2 which is parallel to the x-axis.
(d) From P, draw a perpendicular on y = -2 which meets it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
Then P’ is the image of P, whose co-ordinates are (-3, 1).

Question 9.
The point P ( – 4, – 5) on reflection in y-axis is mapped on P’. The point P’ on reflection in the origin is mapped on P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of point P (-4, -5) in y-axis
∴Co-ordinates of P’ will be (4, -5)
Again P” is the image of P’ under reflection in origin will be (-4, 5).
The single transformation that maps P onto P” is the x-axis

Question 10.
Write down the co-ordinates of the image of the point (3, – 2) when :
(i) reflected in the x-axis
(ii) reflected in the y-axis
(iii) reflected in the x-axis followed by reflection in the y-axis
(iv) reflected in the origin. (2000)
Solution:
Co-ordinates of the given points are (3, -2).
(i) Co-ordinates of the image reflected in x- axis will be (3, 2)
(ii) Co-ordinates of the image reflected in y- axis will be (-3, -2)
(iii) Co-ordinates of the point reflected in x- axis followed by reflection in the y-axis will be (-3, 2)
(iv) Co-ordinates of the point reflected in the origin will be (-3, 2)

Question 11.
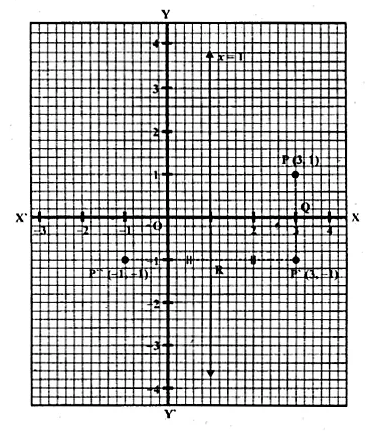
Find the co-ordinates of the image of (3, 1) under reflection in x-axis followed by a reflection in the line x = 1.
Solution:
(i) Draw axis XOX’ and YOY’ taking 1 cm = 1 unit.
(ii) Plot a point P (3, 1).
(iii) Draw a line x = 1, which is parallel to y-axis.
(iv) From P, draw a perpendicular on x-axis meeting it at Q.
(v) Produce PQ to P’ such that QP’ = PQ, then
P’ is the image of P is x-axis. Then co-ordinates of P’ will be (3, -1)
(vi) From P’, draw a perpendicular on x = 1 meeting it at R.
(vii) Produce P’R to P” such that RP” = P’R
∴P” is the image of P’ in the line x = 1
Co-ordinates of P” are (-1, -1)

Question 12.
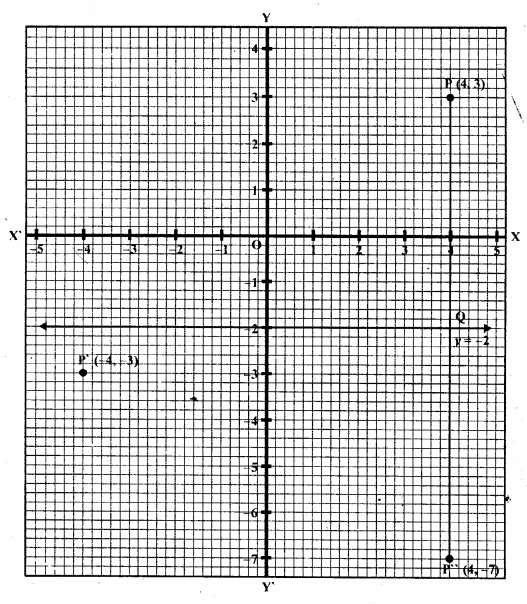
If P’ ( – 4, – 3) is the image of a point P under reflection in the origin, find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P under reflection in the line y = – 2.
Solution:
(i) Reflection of P is P’ (-4, -3) in the origin
∴ Co-ordinates of P will be (4, 3)
Draw a line y = -2, which is parallel to x-axis
(ii) From P, draw a perpendicular on y = -2 meetings it at Q
Produce PQ to P” such that QP” = PQ
∴P” will the image of P in the line y = -2
∴Co-ordinates of P” will be (4, -7)

Question 13.
A Point P (a, b) is reflected in the x-axis to P’ (2, – 3), write down the values of a and b. P” is the image of P, when reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line parallel to y-axis such that x = 4. (1998)
Solution:
P’ (2, -3) is the reflection of P (a, b) in the x-axis
∴Co-ordinates of P’ will be P’ (a, – b) but P’ is (2, -3)
Comparing a = 2, b = 3

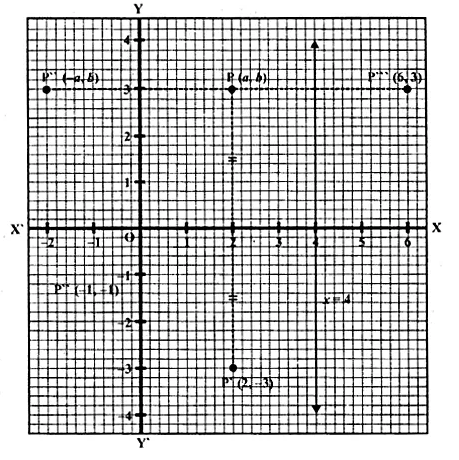
∴Co-ordinates of P will be (2, 3)
P” is the image of P when reflected in y-axis
∴Co-ordinate of P” will be ( – 2, 3)
Draw a line x = 4, which is parallel to y-axis
and P'” is the image of P when it is reflected in the line x = 4,
then P'” is its reflection Co-ordinates of P”‘ will be (6, 3).

Question 14.
(i) Point P (a, b) is reflected in the x-axis to P’ (5, – 2). Write down the values of a and b.
(ii) P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”. (1997)
Solution:
(i) Image of P (a, b) reflected in the x-axis to P’ (5, -2)
∴ a = 5 and b = 2
(ii) P” is the image of P when reflected in the y-axis
∴ its co-ordinates will be (-5, -2).
(iii) The single transformation that maps P’ to P” is the origin.

Question 15.
Points A and B have co-ordinates (2, 5) and (0, 3). Find
(i) the image A’ of A under reflection in the x-axis.
(ii) the image B’ of B under reflection in the line AA’.
Solution:
Co-ordinates of A are (2, 5) and of B are (0, 3)

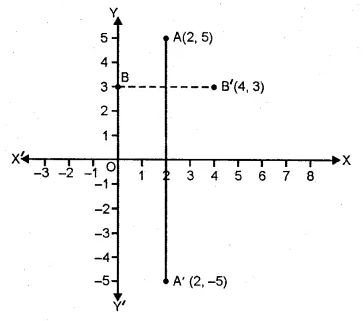
(i) Co-ordinates of A’, the image of A reflected in the x-axis will be (2, -5)
(ii) Co-ordinates of B’, the image of B under reflection in the line AA’ will be (4, 3).

Question 16.
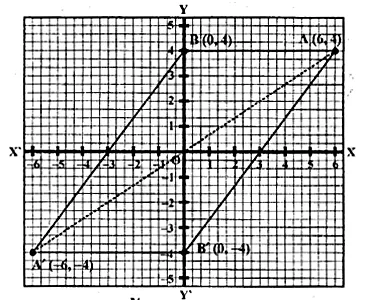
Plot the points A (2, – 3), B ( – 1, 2) and C (0, – 2) on the graph paper. Draw the triangle formed by reflecting these points in the x-axis. Are the two triangles congruent?

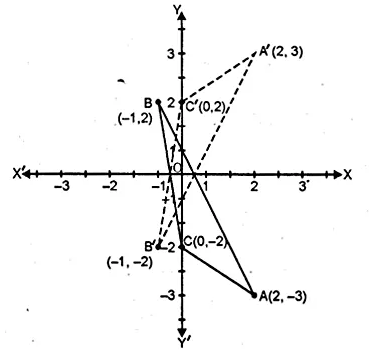
Solution:
The points A (2, -3), B (-1, 2) and C(0, -2) has been plotted on the graph paper as shown and are joined to form a triangle ABC. The co-ordinates of the images of A, B and C reflected in x-axis will be A’ (2, 3), B’ (-1, -2), C’ (0, 2) respectively and are joined to from another ∆ A’B’C’
Yes, these two triangles are congruent.

Question 17.
The points (6, 2), (3, – 1) and ( – 2, 4) are the vertices of a right angled triangle. Check whether it remains a right angled triangle after reflection in the y-axis.
Solution:
Let A (6, 2), B (3, -1) and C (-2, 4) be the points of a right-angled triangle
then the co-ordinates of the images of A, B, C reflected in y-axis be
A’ (-6, 2), B’ (-3, -1) and C’ (2, 4).

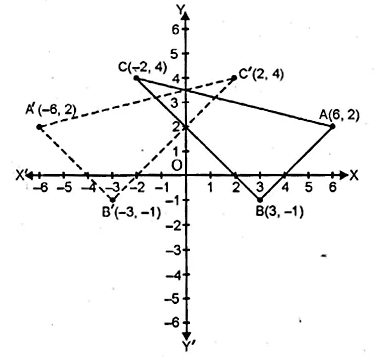
By joining these points, we find that ∆A’B’C’ is also a right angled triangle.

Question 18.
The triangle ABC where A (1, 2), B (4, 8), C (6, 8) is reflected in the x-axis to triangle A’ B’ C’. The triangle A’ B’ C’ is then reflected in.the origin to triangle A”B”C” Write down the co-ordinates of A”, B”, C”. Write down a single transformation that maps ABC onto A” B” C”.
Solution:
The co-ordinates of ∆ ABC are A (1, 2) B (4, 8), C (6, 8)
which are reflected in x- axis as A’, B’ and C’.
∴ The co-ordinates of A’ (1, -2), B (4, -8) and C (6, -8).
A’, B’ and C’ are again reflected in origins to form an ∆A”B”C”.
∴ The co-ordinates of A” will be (-1, 2), B” (-4, 8) and C” (-6, 8)
The single transformation that maps ABC onto A” B” C” is y-axis.

Question 19.
The image of a point P on reflection in a line l is point P’. Describe the location of the line l.
Solution:
The line will be the right bisector of the line segment joining P and P’.

Question 20.
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate
(i) the x-axis
(ii) the y-axis and
(iii) the origin.
Solution:
Q is the image of P on reflection in y-axis
and mid point of PQ is invariant on reflection in x-axis

(i) x-axis will be the line joining the points P and Q.
(ii) The line perpendicular bisector of line segment PQ is the y-axis.
(iii) The origin will be the mid point of line segment PQ.

Question 21.
The point ( – 3, 0) on reflection in a line is mapped as (3, 0) and the point (2, – 3) on reflection in the same line is mapped as ( – 2, – 3).
(i) Name the mirror line.
(ii) Write the co-ordinates of the image of ( – 3, – 4) in the mirror line.
Solution:
The point (-3,0) is the image of point (3, 0)
and point (2, -3) is image of point (-2, -3) reflected on the same line.
(i) It is clear that the mirror line will be y-axis.
(ii) The co-ordinates of the image of the point (-3, -4)
reflected in the same line i.e. y-axis will be (3, -4).

Question 22.
A ( – 2, 4) and B ( – 4, 2) are reflected in the y-axis. If A’ and B’ are images of A and B respectively, find

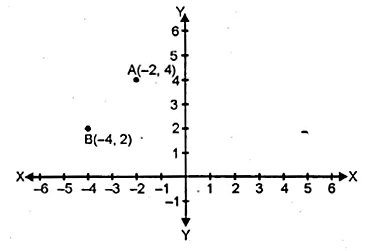
(i) the co-ordinates of A’ and B’.
(ii) Assign special name to quad. AA’B’B.
(iii) State whether AB’ = BA’.
Solution:
A (-2, 4) and B (-4, 2) are reflected in y- axis as A’ and B’.

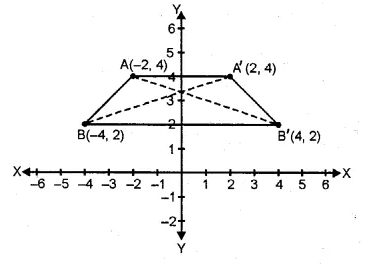
(i) Co-ordinates of A’ are (2, 4) and of B are (4, 2).
(ii) The quadrilateral AA’ B’ B is an isosceles trapezium.
(iii) yes, AB’ = BA’

Question 23.
Use graph paper for this question.
(i) The point P (2, – 4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(ii) Point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR. (2007)
Solution:
(i) Since the point Q is the reflection of the point P (2, -4) in the line x = 0,
the co-ordinates of Q are (2, 4).
(ii) Since R is the reflection of Q (2, 4) about the line y = 0,
the co-ordinates of R are ( – 2, 4).
(iii) Figure PQR is the right angled triangle PQR.

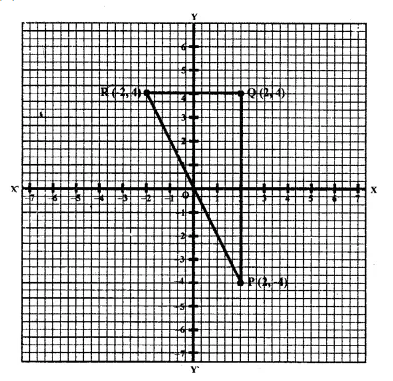
(iv) Area of ∆ PQR = \(\\ \frac { 1 }{ 2 } \) x QR x PQ
= \(\\ \frac { 1 }{ 2 } \) x 4 x 8
= 16 sq. units.

Question 24.
Use graph paper for this question. The point P (5, 3) was reflected in the origin to get the image P’.
(i) Write down the co-ordinates of P’.
(ii) If M is the foot of perpendicular from P to the x-axis, find the co-ordinates of M.
(iii) If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(iv) Name the figure PMP’N.
(v) Find the area of the figure PMP’N. (2001)
Solution:
P’ is the image of point P (5, 3) reflected in the origin.

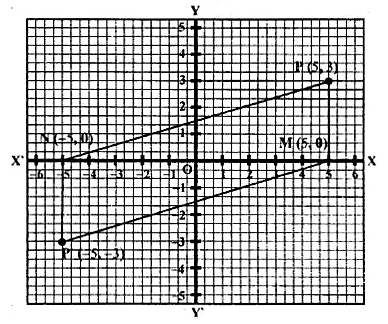
(i) Co-ordinates of P’ will be (-5, -3).
(ii) M is the foot of the perpendicular from P to the x-axis.
Co-ordinates of M will be (5, 0)
(iii) N is the foot of the perpendicular from P’ to x-axis.
Co-ordinates of N will be (-5, 0).
(iv) By joining the points, the figure PMP’N is a parallelogram.
(v) Area of the parallelogram = 2 x area of ∆ MPN
= 2 x \(\\ \frac { 1 }{ 2 } \) x MN x PM = MN x PM
= 10 x 3 = 30 sq. units. Ans.

Question 25.
Using a graph paper, plot the points A (6, 4) and B (0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’B’.
(iv) Find its perimeter.
Solution:
(i) A (6, 4), B (0, 4)

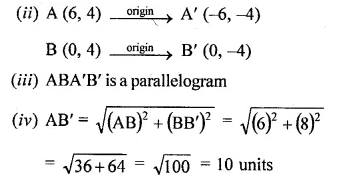
Perimeter = Sum of all sides = 6 + 10 + 6 + 10 = 32 units

Question 26.
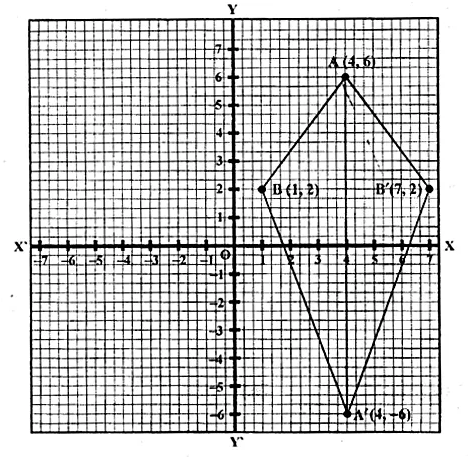
Use graph paper to answer this question
(i) Plot the points A (4, 6) and B (1, 2).
(ii) If A’ is the image of A when reflected in x-axis, write the co-ordinates of A’.
(iii) If B’ is the image of B when B is reflected in the line AA’, write the co-ordinates of B’.
(iv) Give the geometrical name for the figure ABA’B’. (2009)
Solution:
(i) Plotting the points A (4, 6) and B (1, 2) on the given graph.
(ii) A’ = (4, -6)
(iii) B’ = (7, 2)
(iv) In the quadrilateral ABA’B’, we have AB = AB’ and A’B = A’B’
Hence, ABA’B’ is a kite.

Question 27.
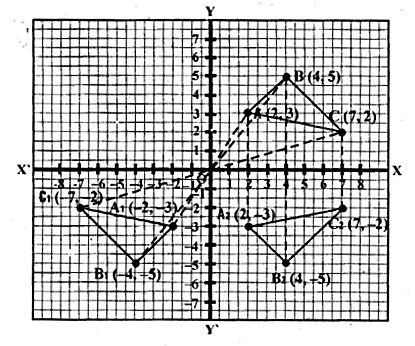
The points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ABC. (2006)
(i) Write down the co-ordinates of A1, B1, C1 if ∆ A1B1C1 is the image of ∆ ABC when reflected in the origin.
(ii) Write down the co-ordinates of A2, B2, C2 if ∆ A2B2C2 is the image of ∆ ABC when reflected in the x-axis.
(iii) Assign the special name to the quadrilateral BCC2B2 and find its area.


Solution:
Points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ ABC.
A1, B1 and C1 are the images of A, B and C reflected in the origin.
(i) Co-ordinates of A1 = (-2, -3) of B1 (-4, -5) and of C1 (-7, -2).
(ii) Co-ordinates of A2, B2 and C2 the images of A, B and C
when reflected in x-axis are A2 (2, – 3), B2 (4, – 5), C2 (7, – 2)
(iii) The quadrilateral formed by joining the points,
BCC2B2 is an isosceles trapezium and its area

Question 28.
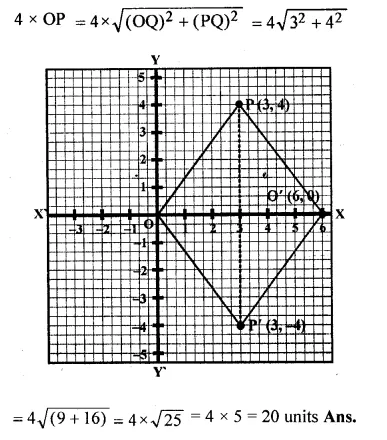
The point P (3, 4) is reflected to P’ in the x-axis and O’ is the image of O (origin) in the line PP’. Find :
(i) the co-ordinates of P’ and O’,
(ii) the length of segments PP’ and OO’.
(iii) the perimeter of the quadrilateral POP’O’.
Solution:
P’ is the image of P (3, 4) reflected in x- axis
and O’ is the image of O the origin in the line P’P.
(i) Co-ordinates of P’ are (3, -4)
and co-ordinates of O’ reflected in PP’ are (6, 0)
(ii) Length of PP’ = 8 units and OO’ = 6 units
(iii) Perimeter of POP’O’ is

Question 29.
Use a graph paper for this question. (Take 10 small divisions = 1 unit on both axes). P and Q have co-ordinates (0, 5) and ( – 2, 4).
(i) P is invariant when reflected in an axis. Name the axis.
(ii) Find the image of Q on reflection in the axis found in (i).
(iii) (0, k) on reflection in the origin is invariant. Write the value of k.
(iv) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis. (2005)
Solution:

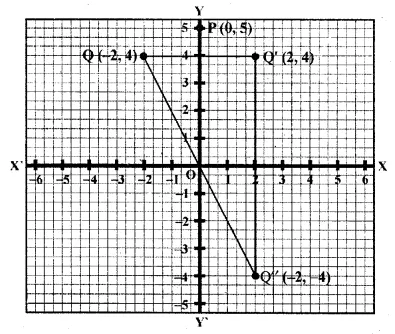
(i) Two points P (0, 5) and Q (-2, 4) are given As the abscissa of P is 0.
It is invariant when is reflected in y-axis.
(ii) Let Q’ be the image of Q on reflection in y-axis.
Co-ordinate of Q’ will be (2, 4)
(iii) (0, k) on reflection in the origin is invariant.
co-ordinates of image will be (0, 0). k = 0
(iv) The reflection of Q in the origin is the point Q”
and its co-ordinates will be (2, – 4)
and reflection of Q” (2, – 4) in x-axis is (2, 4) which is the point Q’

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.