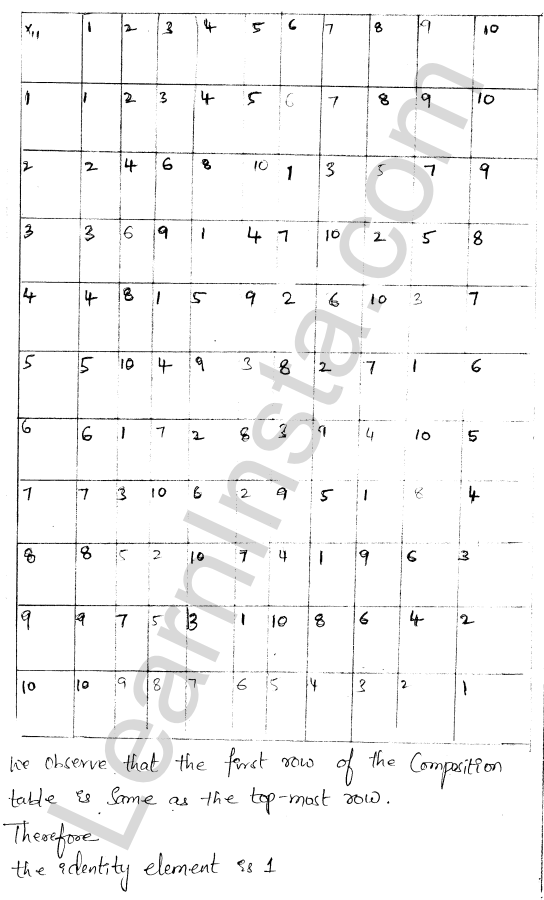
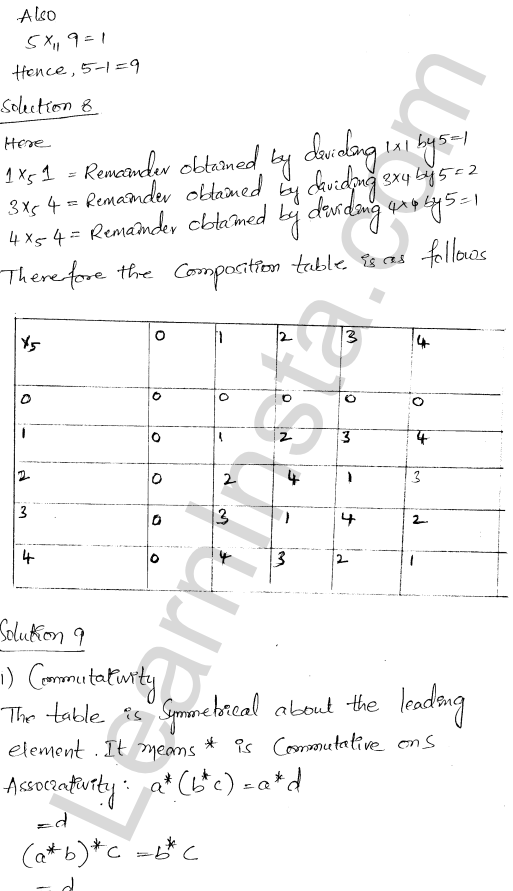
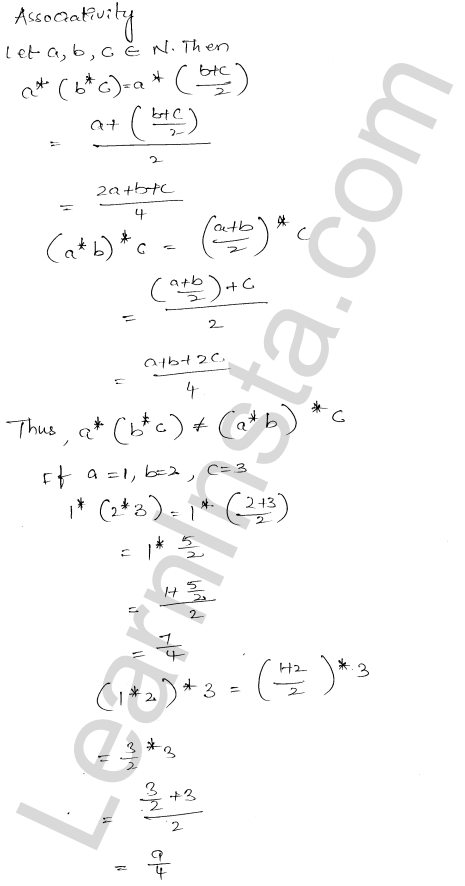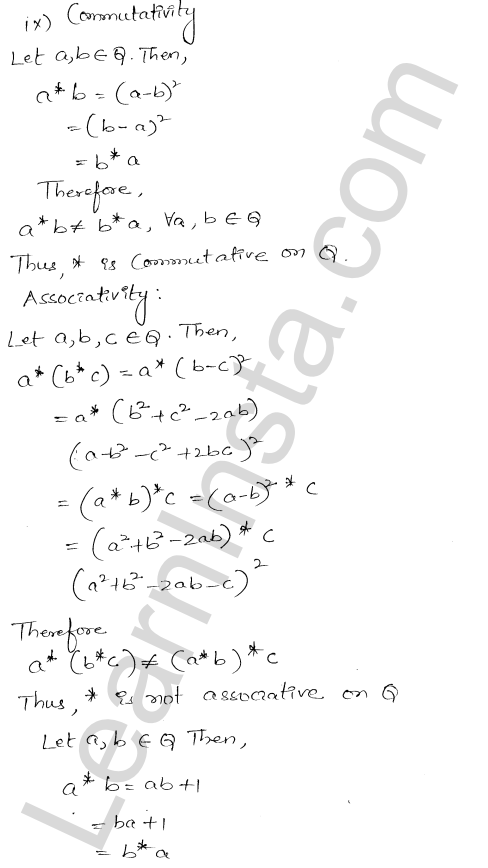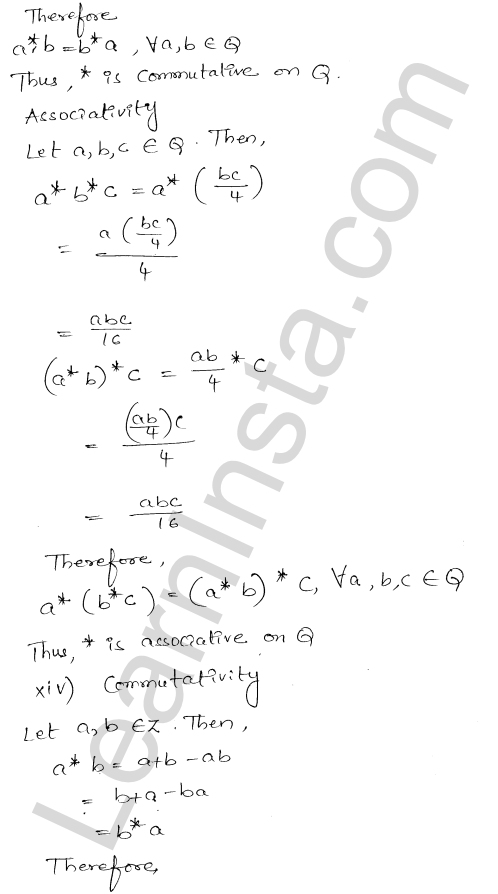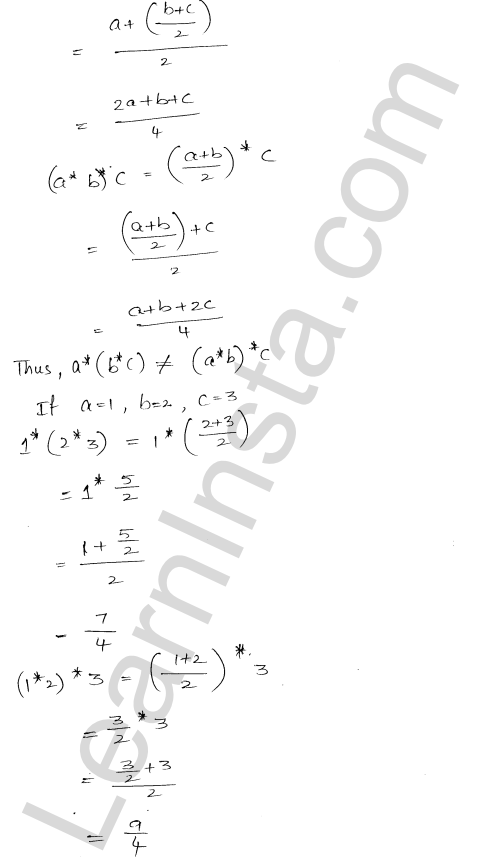RD Sharma Class 12 Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1 are part of RD Sharma Class 12 Solutions. Here we have given RD Sharma Class 12 Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1.
Here you can get free RD Sharma Solutions for Class 12 Maths of Chapter 4 Inverse Trigonometric Functions Exercise 4.1. All RD Sharma Book Solutions are given here exercise wise for Inverse Trigonometric Functions. RD Sharma Solutions are helpful in the preparation of several school level, graduate and undergraduate level competitive exams. Practicing questions from RD Sharma Mathematics Solutions for Class 12 Chapter 4 Inverse Trigonometric Functions is proven to enhance your math skills.
| Class: | 12th Class |
| Chapter: | Chapter 4 |
| Name: | Inverse Trigonometric Functions |
| Exercise: | Exercise 4.1 |
RD Sharma Class 12 Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1
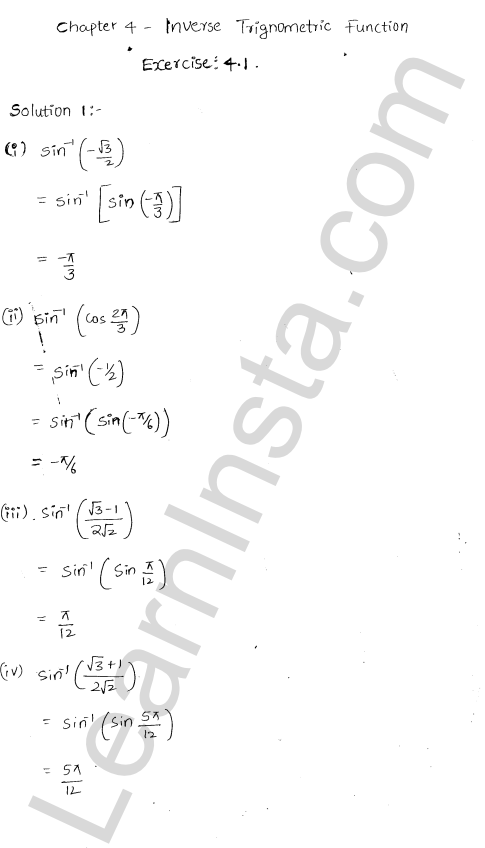





We hope the RD Sharma Class 12 Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1, help you. If you have any query regarding RD Sharma Class 12 Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1, drop a comment below and we will get back to you at the earliest.