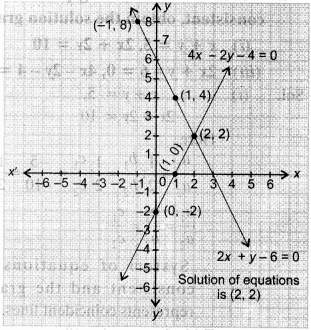
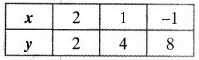
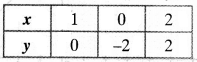
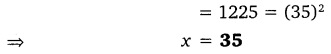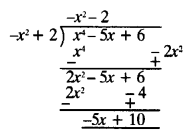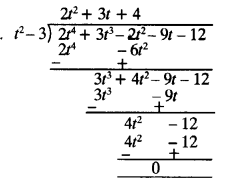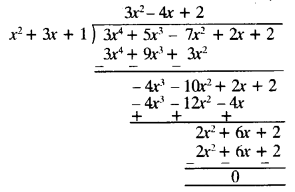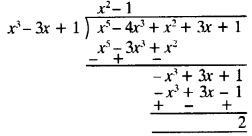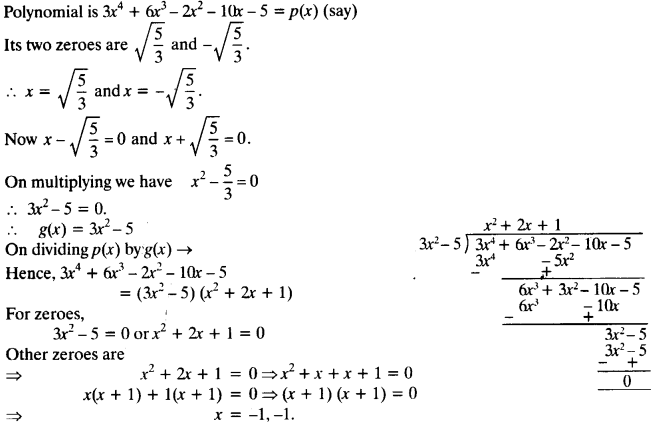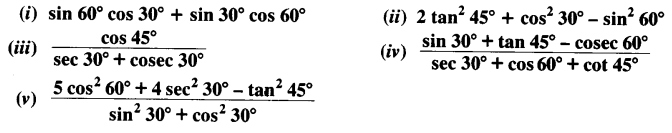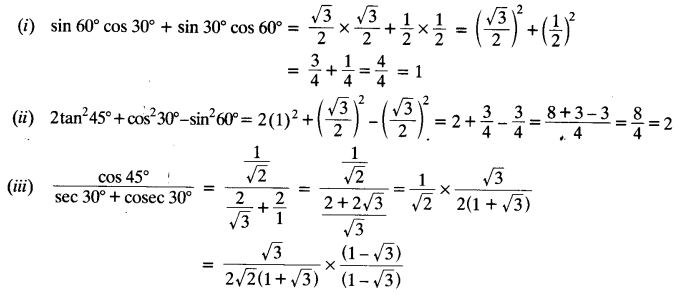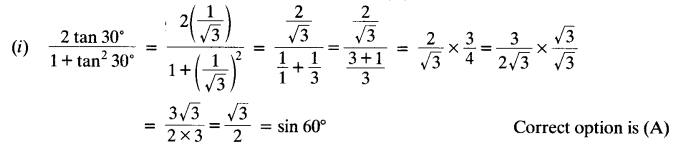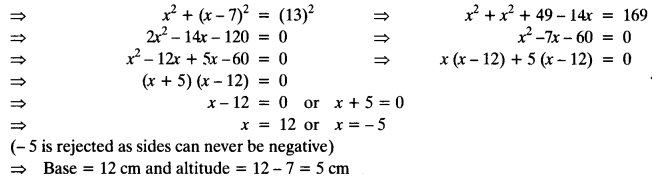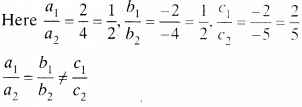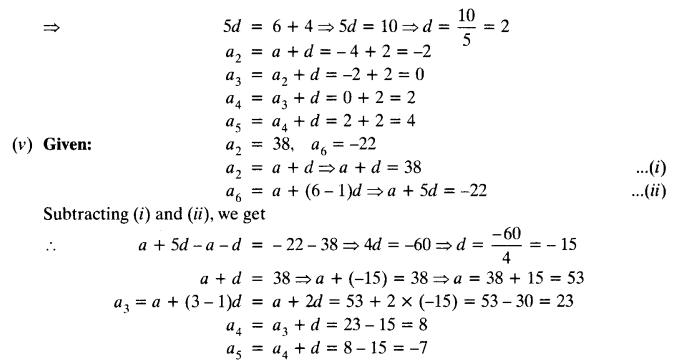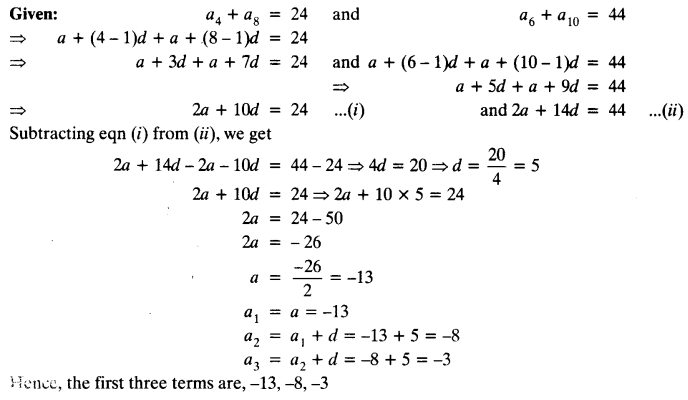NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.4 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.4.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Real Numbers |
| Exercise | Ex 1.4 |
| Number of Questions Solved | 3 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4
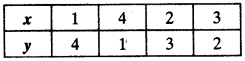
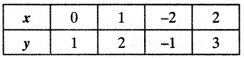
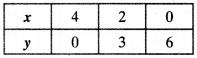
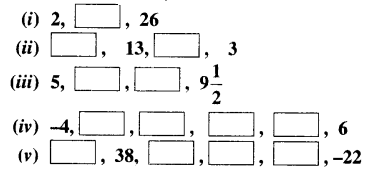
Ex 1.4 Class 10 Question 1.
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

Solutions:


Ex 1.4 Class 10 NCERT Solutions Question 2.
Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solutions:
In Question 1, (i), (ii), (iv), (vi), (viii) and (ix) are having terminating decimal expansion.
![]()
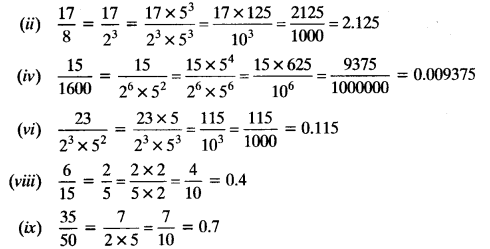
Class 10 Ex 1.4 Question 3.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form \(\frac { p }{ q }\), what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000…
(iii) 43. \(\overline { 123456789 }\)
Solutions:
(i) 43.123456789
Since the decimal expansion terminates,so the given real number is rational and therefore of the form \(\frac { p }{ q }\)
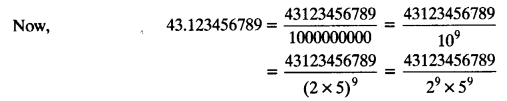
Here, q = 29 x 59, So prime factorisation of q is of the form 2n x 5m.
(ii) 0.120120012000120000…
Since the decimal expansion is neither terminating nor non-terminating repeating, therefore the given real number is not rational.
(iii) 43. \(\overline { 123456789 }\)
Since the decimal expansion is non-terminating repeating, therefore the given real number is rational and therefore of the form \(\frac { p }{ q }\)
Let x = 43. \(\overline { 123456789 }\) = 43.123456789123456789… ….(i)
Multiply both sides of (i) by 1000000000, we get

We hope the NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.4 help you. If you have any query regarding NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.4, drop a comment below and we will get back to you at the earliest.