NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 8 |
| Chapter Name | Introduction to Trigonometry |
| Exercise | Ex 8.4 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:
From trigonometric identity, cosec² A – cot² A = 1, we get
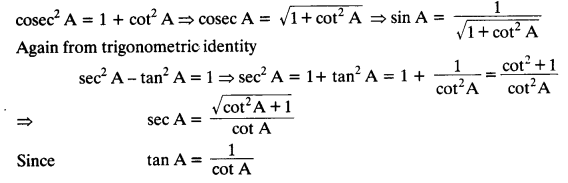
Question 2.
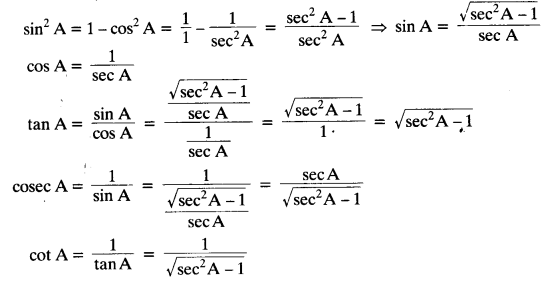
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Since sin² A + cos² A = 1, therefore
Question 3.
Evaluate:
(i)
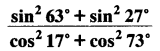
(ii) sin 25° cos 65° + cos 25° sin 65°
Solution:
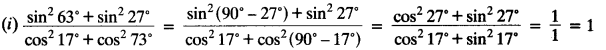
(ii) sin 25° cos 65° + cos 25° sin 65° = sin 25° cos (90° – 25°) + cos 25° sin (90° – 25°)
= sin 25° sin 25° + cos 25° cos 25°
= sin² 25° + cos² 25° = 1
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ ) =
(A) 0
(B) 1
(C) 2
(D) -1
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\)
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A
Solution:
(i) 9 sec² A – 9 tan² A = 9(sec² A – tan² A) = 9 x 1 = 9
Correct option is (B)
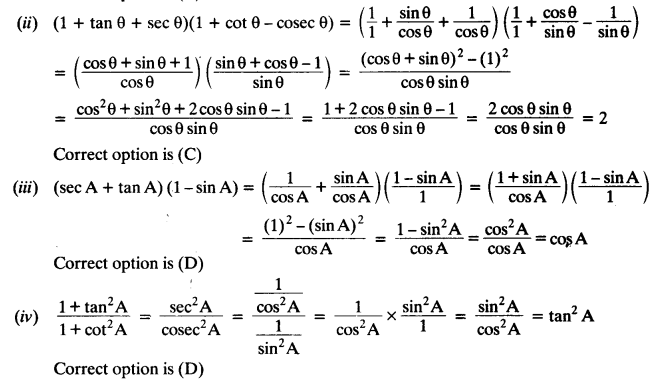
Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
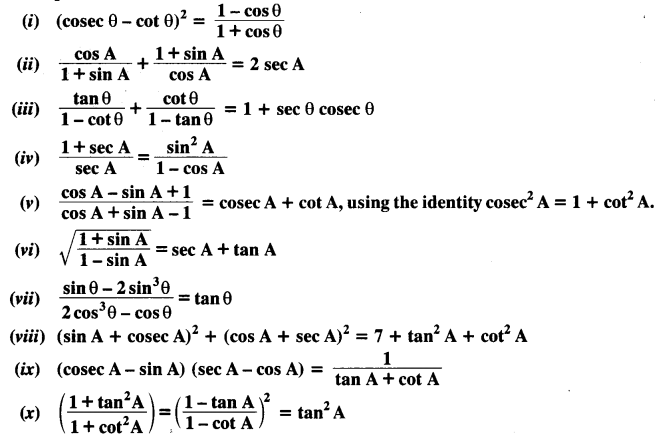
Solution:



We hope the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4, drop a comment below and we will get back to you at the earliest.
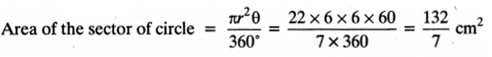
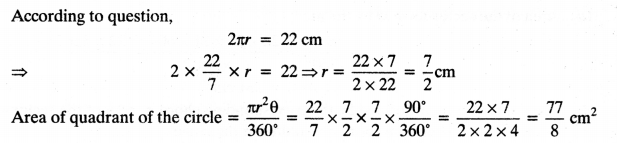
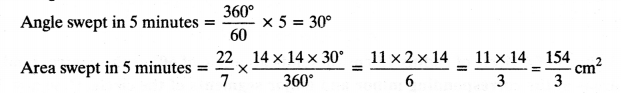

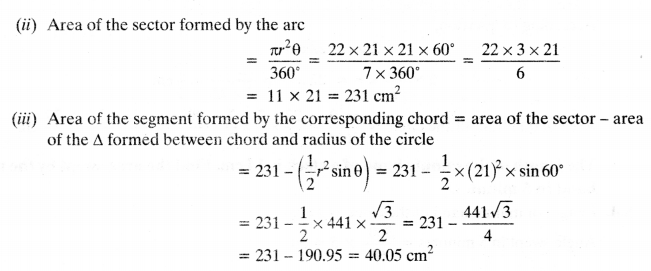
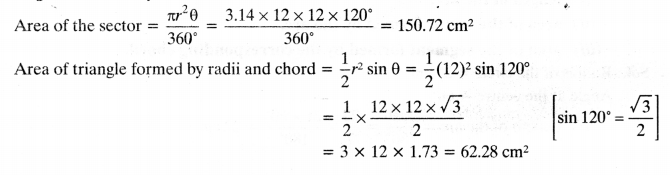
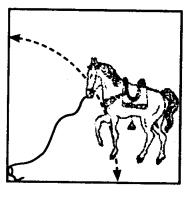
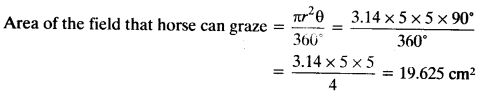
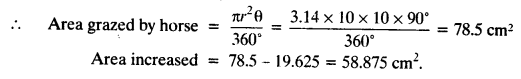


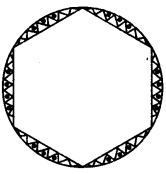
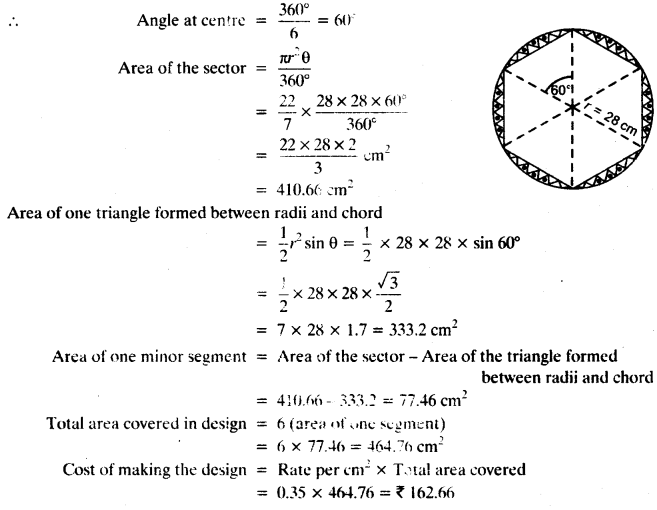
 On this page, you will find NCERT Class 10 Economics Chapter 5 Notes Pdf free download. CBSE
On this page, you will find NCERT Class 10 Economics Chapter 5 Notes Pdf free download. CBSE  On this page, you will find NCERT Class 10 Civics Chapter 8 Notes Pdf free download. CBSE
On this page, you will find NCERT Class 10 Civics Chapter 8 Notes Pdf free download. CBSE  On this page, you will find NCERT Class 10 Civics Chapter 5 Notes Pdf free download. CBSE
On this page, you will find NCERT Class 10 Civics Chapter 5 Notes Pdf free download. CBSE  On this page, you will find NCERT Class 10 Civics Chapter 3 Notes Pdf free download. CBSE
On this page, you will find NCERT Class 10 Civics Chapter 3 Notes Pdf free download. CBSE  On this page, you will find Management of Natural Resources Class 10 Notes Science Chapter 16 Pdf free download. CBSE NCERT
On this page, you will find Management of Natural Resources Class 10 Notes Science Chapter 16 Pdf free download. CBSE NCERT 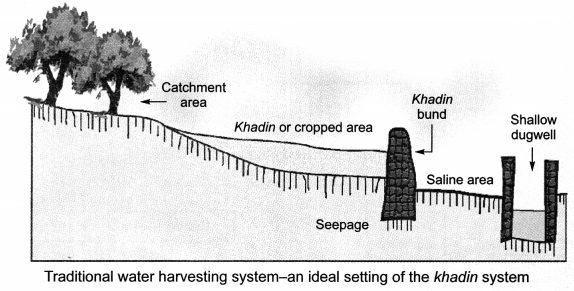
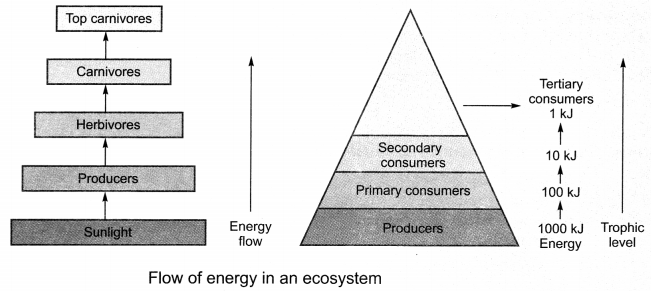
 On this page, you will find Our Environment Class 10 Notes Science Chapter 15 Pdf free download. CBSE NCERT
On this page, you will find Our Environment Class 10 Notes Science Chapter 15 Pdf free download. CBSE NCERT 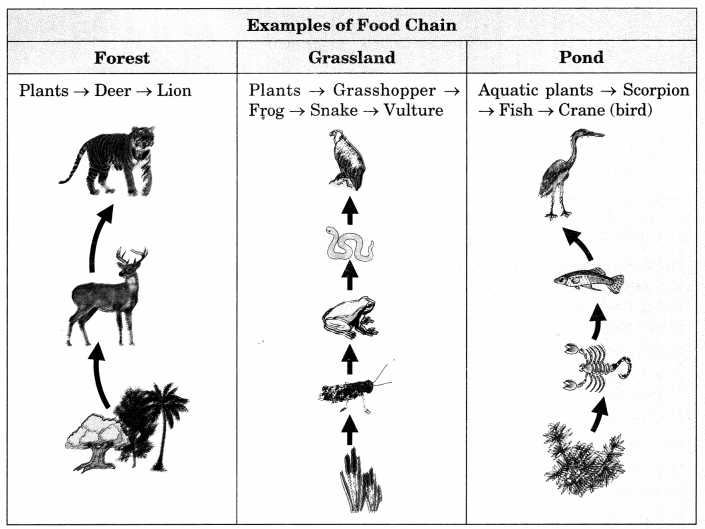
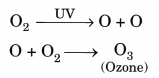
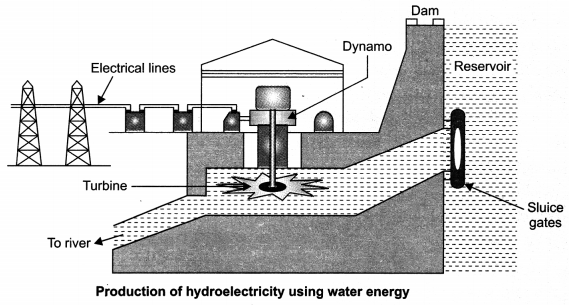
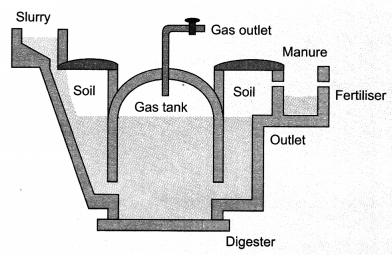
 On this page, you will find Sources of Energy Class 10 Notes Science Chapter 14 Pdf free download. CBSE NCERT
On this page, you will find Sources of Energy Class 10 Notes Science Chapter 14 Pdf free download. CBSE NCERT