Category: CBSE Class 11

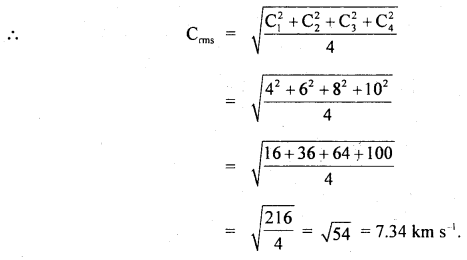
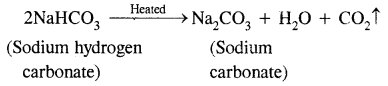
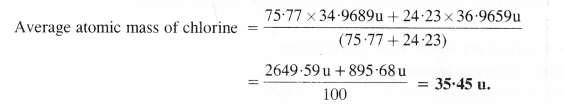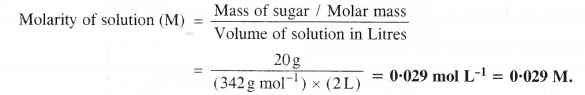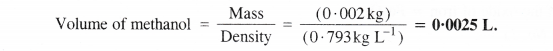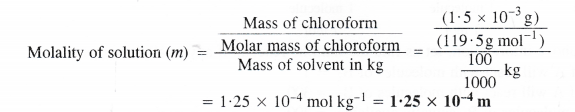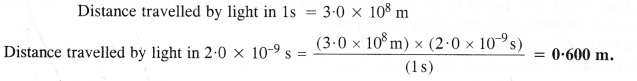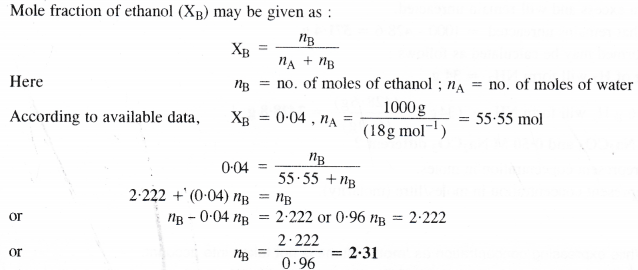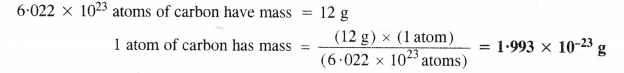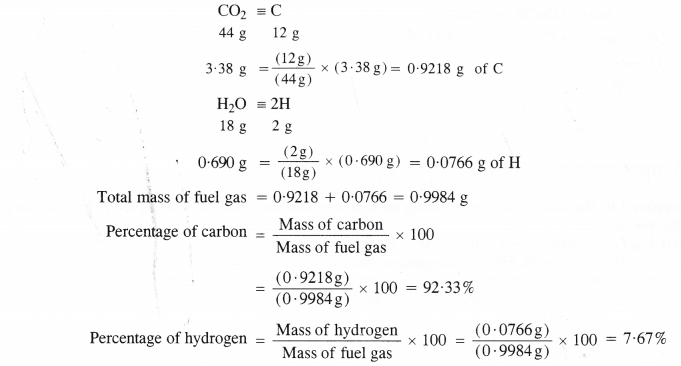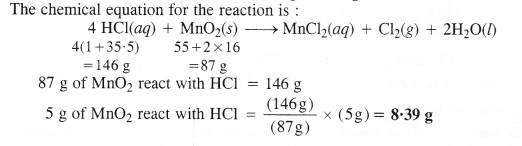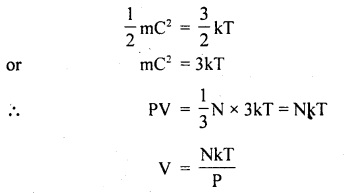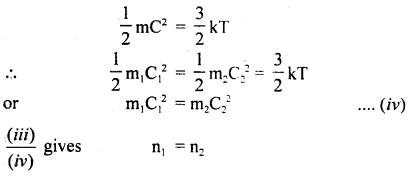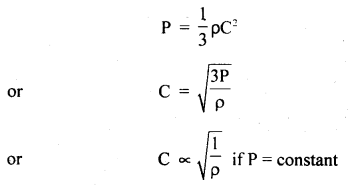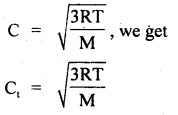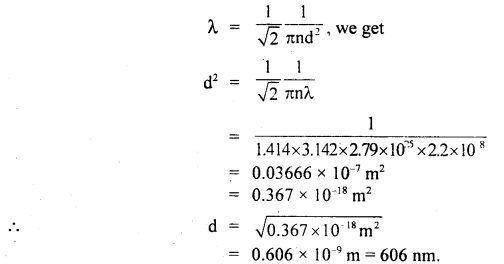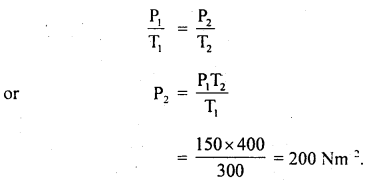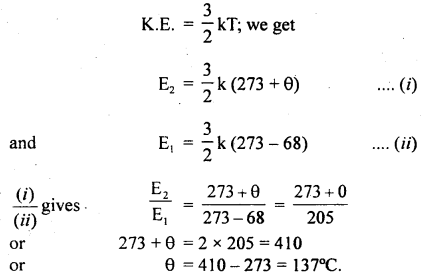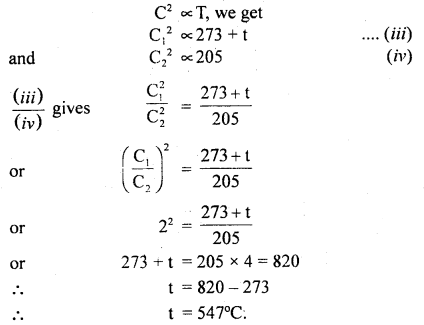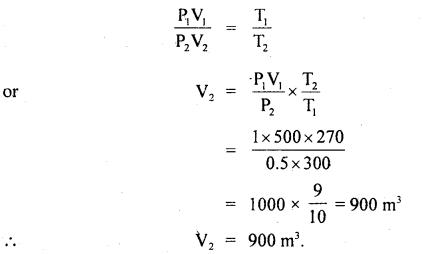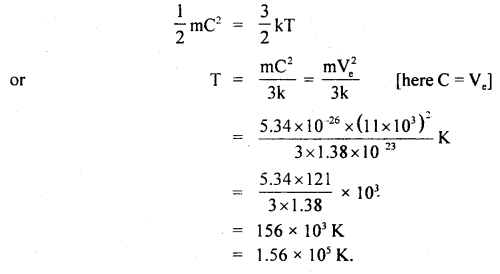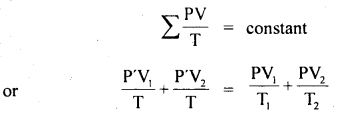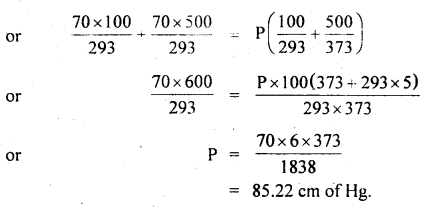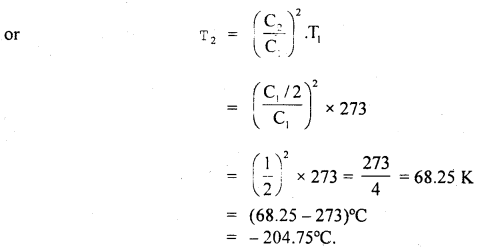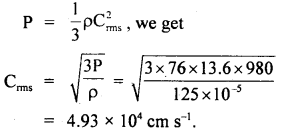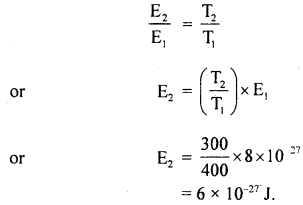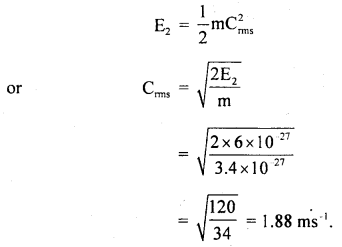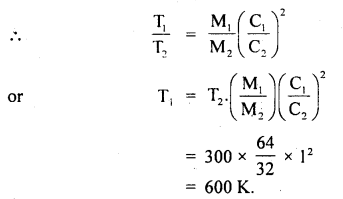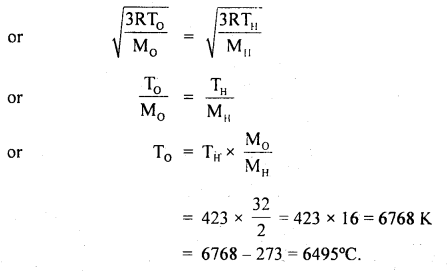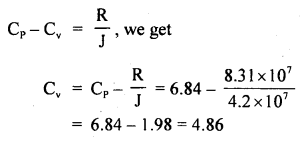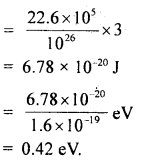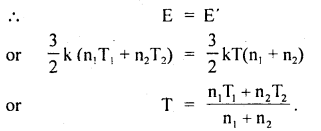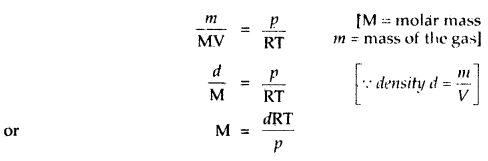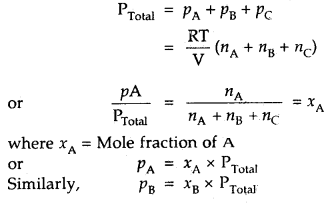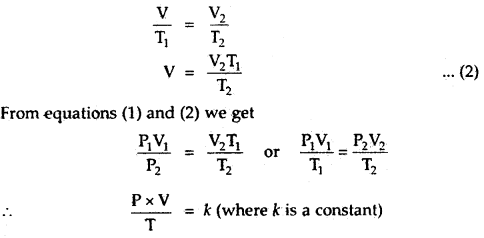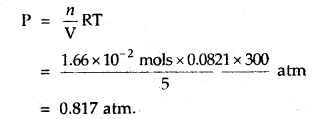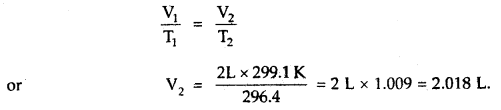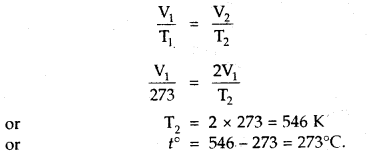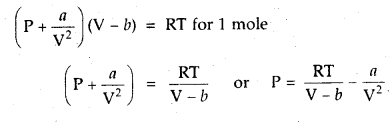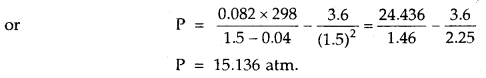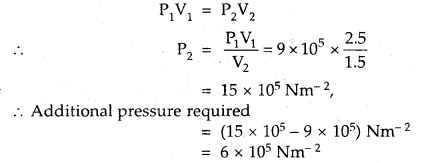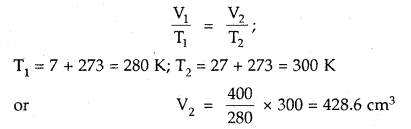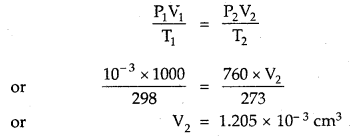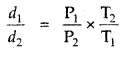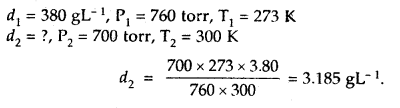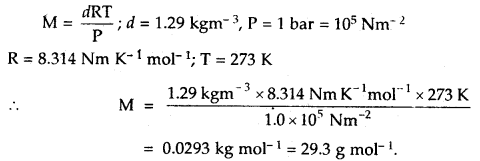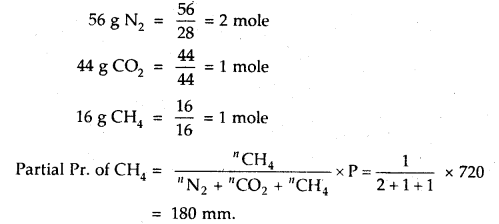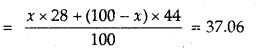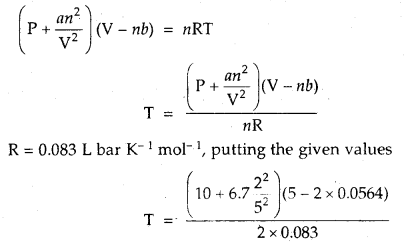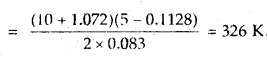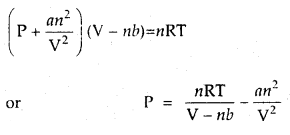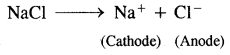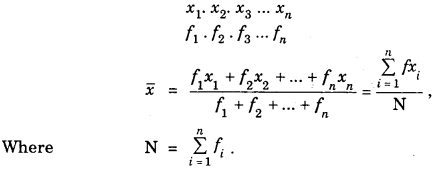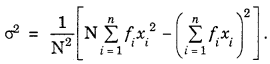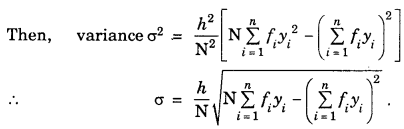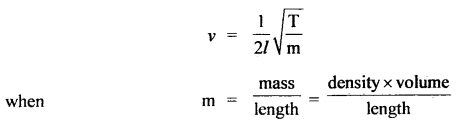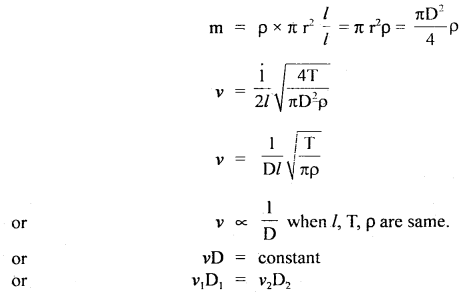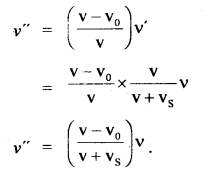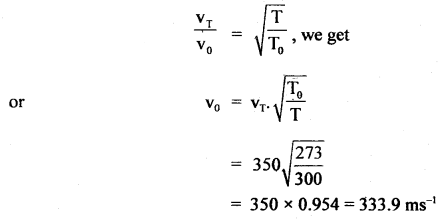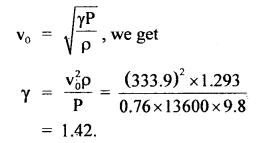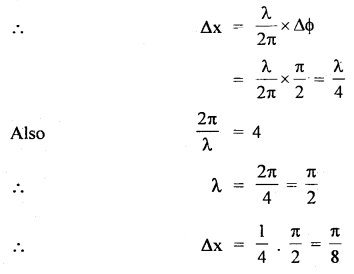Here we are providing Class 11 chemistry Important Extra Questions and Answers Chapter 6 Thermodynamics. Chemistry Class 11 Important Questions are the best resource for students which helps in Class 11 board exams.

Class 11 Chemistry Chapter 6 Important Extra Questions Thermodynamics

Thermodynamics Important Extra Questions Very Short Answer Type

Question 1.
Under what conditions the heat evolved or absorbed is equal to the internal energy change?
Answer:
At constant volume.

Question 2.
What is the sign of AH for endothermic reactions and why?
Answer:
AH is positive as ΔH = H_p – H_r and H_r < H_p.

Question 3.
What is the relationship between the standard enthalpy of formation and the enthalpy of a compound?
Answer:
They are equal.

Question 4.
Why enthalpy of neutralization of HF is greater than 57.1 kJ mol^-1?
Answer:
This is due to the high hydration energy of fluoride ions.

Question 5.
What are the specific heat capacity and molar heat capacity for water?
Answer:
Specific heat capacity for H₂O = 4.18 JK^-1 g^-1
Molar heat capacity for H₂O = 4.18 × 18 = 75.24 JK^-1 mol^-1.

Question 6.
Why enthalpy of neutralization is less if either the acid or the base or both are weak?
Answer:
A part of the heat is used up for dissociation of the weak acid or weak base or both.

Question 7.
What do you mean by a system?
Answer:
A specified part of the universe that is under thermodynamic observation is called a system.

Question 8.
Define a cyclic process.
Answer:
A process in which a system undergoes a series of changes and ultimately returns to the original state is called a cyclic process. For a cyclic process; ΔU = 0.

Question 9.
Why the entropy of a diamond is less than that of graphite?
Answer:
Diamond is more compact than graphite.

Question 10.
Under what conditions, ΔH of a process is equal to ΔU?
Answer:
At constant temperature and constant volume.

Question 11.
Is the enthalpy of neutralization of HCl is same as that of H2S04? If so, why?
Answer:
Yes. Because both are strong acids and ionized almost completely in aqueous solutions.

Question 12.
Which is a better fuel for the animal body: proteins or carbohydrates?
Answer:
Carbohydrates. They have high calorific value.

Question 13.
Is the experimental determination of enthalpy of formation of CH₄ possible?
Answer:
No.

An online enthalpy calculator is specially designed to calculate exact amount of enthalpy generated in a thermodynamic system.

Question 14.
Can we calculate ΔH of every process from the bond energy data of reactants and products?
Answer:
No.

Question 15.
Define enthalpy of fusion.
Answer:
It is defined as the heat change when one mole of solid changes to its liquid form at its melting point. ‘

Question 16.
For the reaction NaCl (aq) + AgNO₃ (aq) → AgCl(s) + NaNO₃(aq), will ΔH be greater than, equal to or less than ΔE?
Answer:
ΔH will be ΔE.

Question 17.
Write the mathematical relationship between heat, internal energy, and work done on the system.
Answer:
ΔE = q + w.

Question 18.
What is the limitation of the I law of thermodynamics?
Answer:
It cannot tell us about the direction of the process

Question 19.
What is the relationship between ΔH and ΔE?
Answer:
ΔH = ΔE + PΔV = ΔE + Δn_gRT.

Question 20.
State the I law of thermodynamics.
OR
State the Law of conservation of energy.
Answer:
The energy of an isolated system remains conserved.
OR
The energy can neither be created nor destroyed, though it can be converted from one form into another.

Question 21.
Which of the following is a state function?
(i) height of a hill
(ii) distance traveled in climbing the hill
(iii) energy consumed in climbing the hill.
Answer:
Energy consumed in climbing the hill.

Question 22.
What is the internal energy of one mole of a noble gas?
Answer:
U = \(\frac{3}{2}\)RT.

Question 23.
Which of the following are state functions?
(i) q
(ii) heat capacity
(iii) specific heat capacity
(iv) ΔH and ΔU.
Answer:
(iii) specific heat capacity and
(iv) ΔH and ΔU

Question 24.
Name the two most common modes by which a system and surroundings exchange their energy?
Answer:
Heat and work.

Question 25.
What will happen to internal energy if work is done by the system?
Answer:
The internal energy of the system will decrease.

Question 26.
How many times is the molar heat capacity greater than the specific heat capacity of water?
Answer:
18 times.

Question 27.
Neither q nor w is a state function but q + w is a state function. Why?
Answer:
q + w is equal to ΔU, which is a state function.

Question 28.
Name the state function Which remains constant during an isothermal change.
Answer:
Temperature.

Question 29.
What is the value of enthalpy of neutralization of a strong acid and a strong base?
Answer:
– 57.1 kJ/gm equivalent.

Question 30.
Out of 1 mole of H₂O(g) and 1 mole of H₂O(l) which one will have greater entropy?
Answer:
H₂O(g) will have greater entropy.

Question 31.
When a substance is said to be in its standard state?
Answer:
When it is present at 298 K and under one atmospheric pressure.

Question 32.
What is the entropy of the formation of an element in its standard state?
Answer:
By convention, the enthalpies (heats) of the formation of all elements in their most stable form (standard state) is taken as zero.

Question 33.
What is the physical significance of free energy change of a system?
Answer:
The decrease in free energy (- ΔG) is a measure of useful work or network obtainable during the process at constant temp and pressure.

Question 34.
Why is it essential to mention the physical state of reactants and products in thermochemical reactions?
Answer:
It is because the physical state of reactants and products also contributes significantly to the value ΔU or ΔH.

Question 35.
Name two intensive and extensive properties of a system.
Answer:

• Intensive properties: Viscosity, refractive index.
• Extensive properties: Mass, volume, heat capacity, etc.

Question 36.
What is fuel value or calorific value?
Answer:
It is defined as the amount of heat released when 1 gm of fuel or food is burnt completely in air or oxygen.

Question 37.
Is the process of diffusion of gases enthalpy driven or entropy-driven?
Answer:
It is an entropy-driven process.

Question 38.
The value of ΔHsol of NaNO₃ is positive, yet the dissolution is spontaneous, why?
Answer:
There is a large increase in entropy i.e., it is an entropy-driven process.

Question 39.
Write a thermochemical equation of enthalpy of combustion of methanol.
Answer:
2CH₃OH(l) + 3O₂(g) → 2CO₂(g) + 4H₂O(1); ΔH = – Q kJ
where Q kJ mol-1 is the enthalpy of combustion.

Question 40.
What is the enthalpy of the formation of Cl₂?
Answer:
Enthalpy of formation of a homonuclear molecule like Cl₂ is zero.

Question 41.
For a reaction also ΔH and ΔS are positive. What is the condition that this reaction occurs spontaneously?
Answer:
To make ΔG negative TΔS > ΔH.

Question 42.
Arrange the following fuels in order of increasing fuel efficiency; kerosene, diesel oil, wax, natural gas.
Answer:
Lower hydrocarbons have higher calorific value and thus are more efficient.
wax < diesel oil < kerosene < natural gas.

Question 43.
What is the sign of ΔS when N₂ and H₂ combine to form NH₃?
Answer:
ΔS is negative as the number of molecules decreases.

Question 44.
How will compare the efficiency of the three given fuels?
Answer:
By comparing their calorific values. Larger the calorific value, the greater the fuel efficiency.

Question 45.
How is a non-spontaneous process made spontaneous?
Answer:
By continuously supplying energy to it from outside.

Question 46.
What is the expression for entropy change for a phase transition? ‘
Answer:
ΔS = \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}\)

Question 47.
Give an example of an isolated system.
Answer:
Thermos.

Question 48.
Is the enthalpy of formation of SnCl₂(s) the same as that of ZnCl₂(s)?
Answer:
No. They are different.

Question 49.
Why we usually study enthalpy change and not internal energy change?
Answer:
Most of the processes including reactions are carried out in open vessels at constant pressure.

Question 50.
What is the enthalpy of one mole of a noble gas?
Answer:
H = U + PV = \(\frac{3}{2}\) RT + RT = \(\frac{5}{2}\) RT.

Question 51.
Which of the thermodynamic properties out of U, S, T, P, V, H, and G are intensive properties and why?
Answer:
T and P, because they depend only upon the nature of the substance.

Question 52.
What is the relationship between q_p and q_v?
Answer:
q_p = q_v + Δng RT, where Δn = n_p– n_r (gaseous).

Question 53.
What is the Gibb’s Helmholtz equation?
Answer:
ΔG = ΔH – TΔS, where ΔG, ΔH, and ΔS are free energy change, enthalpy change, and entropy change respectively.

Question 54.
Comment on the bond energies of four C-H bonds present in CH4?
Answer:
The bond energies of 1st, 2nd, 3rd, and 4th C-H bonds are not equal and so average values are taken.

Question 55.
What is the main limitation of the first law of thermodynamics?
Answer:
It cannot predict the spontaneity of a process.

Question 56.
What is entropy?
Answer:
Entropy is a measure of the randomness/disorder of a system.

Question 57.
A reversible reaction has ΔG° negative for forwarding reaction. What will be the sign of ΔG° for the backward reaction?
Answer:
Negative.

Question 58.
What is the effect of increasing temperature on the entropy of a substance?
Answer:
It increases.

Question 59.
When is the entropy of a perfectly crystalline solid zero?
Answer:
At absolute zero (O.K).

Question 60.
What is an adiabatic process?
Answer:
In which no eat flow between the system and surroundings.

Thermodynamics Important Extra Questions Short Answer Type

Question 1.
Ice is lighter than water, but the entropy of ice is less than that of water. Explain.
Answer:
Water is the liquid form while ice is its solid form. Molecular motion in ice is restricted than in water, i.e., a disorder in ice is restricted than water, i.e., a disorder in ice is less than in water.

Question 2.
Define spontaneity or-feasibility of a process.
Answer:
Spontaneity or feasibility of a process means its inherent tendency to occur on its own in a particular direction under a given set of conditions.

Question 3.
Enthalpy of neutralization of CH₃COOH and NaOH is 55.9 kJ. What is the value of ΔH for ionization of CH₃COOH?
Answer:
The heat of neutralization of strong acid and strong base + ΔH of ionization of CH₃COOH = Enthalpy of neutralization of CH₃COOH and NaOH
∴ – 57.1 kJ + ΔH of ionisation of CH₃COOH = – 55.9 kJ
∴ ΔH of ionisation of CH₃COOH = (- 55.9 + 57.1) kJ
= 1.2 kJ.

Question 4.
When 1 gm of liquid naphthalene (C10H8) solidifies, 150 J of heat is evolved. What is the enthalpy of fusion of C₁₀H₈?
Answer:
ΔHsolidifcation = – 150 × 128 = – 19200 J = – 19.2 kJ
[∵ M.wt.of C₁₀H₈ = 128]

Question 5.
Why most of the exothermic processes (reactions) are spontaneous?
Answer:
ΔG = ΔH – TΔS; For exothermic reactions,
ΔH is -ve For a spontaneous process ΔG is to be -ve.

Thus decrease in enthalpy (- AH) contributes significantly to the driving force (To make ΔG negative).

Question 6.
What is meant by the term state function? Give examples.
Answer:
A state function is a thermodynamic property that depends upon the state of the system and is independent of the path followed to bring about the change. Internal energy change (ΔU), enthalpy change (ΔH) entropy change (ΔS), and free energy change (ΔG) are examples.

Question 7.
The enthalpy of combustion of sulfur is 297 kJ.
Write the thermochemical equation for the combustion of sulfur. What is the value of Δ_fH of SO₂?
Answer:
S(s) + O₂(g) → SO₂(g); Δ_fH = – 297 kJ
∴ ΔH of SO₂ = – 297 kJ mol^-1

Question 8.
What would be the heat released when 0.35 mol of HC1 in solution is neutralized by 0.25 mol of NaOH solution?
Answer:
HCl and NaOH being strong acid and strong- base is completely ionization in dilute aqueous solutions. The net reaction is H + (0.25 mol) + OH^– (0.25. mol) → H₂O (0.25 mol)

Now the heat of neutralization of 1 mole of a strong acid is – 57.1 kJ
∴ The heat released will be 57.1 × 0.25 kJ = 14.27 kJ.

Question 9.
Predict which of the following entropy increases/ decreases?
(i) A liquid crystallizes into a solid.
Answer:
After crystallization molecules attain an ordered state and therefore entropy decreases.

(ii) Temperature bf a crystalline solid is raised from 0 K to 115 K.
Answer:
When the temperature is raised, a disorder in molecules increases, and therefore entropy increases.

(iii) 2NaHCO₃(s) → Na₂CO₃(s) + CO₂(g) + H₂O(g)
Answer:
The reactant is solid and hence has low entropy. Among the products there are two gases and be solid, therefore products represent a condition of higher entropy.

(iv) H₂(g) → 2H(g).
Answer:
Here 2 moles of H atoms have higher entropy than one mole of the hydrogen molecule.

Question 10.
Discuss the effect of temperature on the spontaneity of reactions.
Answer:
Effect of temperature on the spontaneity of reactions:

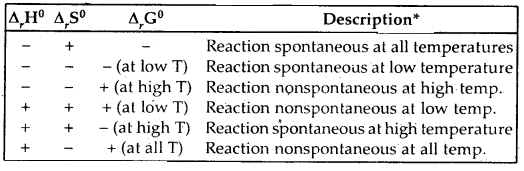
The terms low temperature and high temperature are relative. For a particular reaction, the high temperature could even mean room temperature.

Question 11.
What is the most important condition for a process to be reversible in thermodynamics?
Answer:
The process should be carried out infinitesimally slowly or the driving force should be infinitesimally greater than the opposing force.

Question 12.
Why heat is not a state function?
Answer:
According to first law of Thermodynamics; ΔU = q + w or q – = ΔU – w. As ΔU is a state function, but w is not a state function, therefore q is also not a state function.

Question 13.
Why the absolute value of enthalpy cannot be determined?
Answer:
As H = U + PV
The absolute value of U – the internal energy cannot be determined as it depends upon various factors whose value, cannot be determined.
∴ The absolute value of H cannot be determined.

Question 14.
Which of the following is/are exothermic and which are endothermic?
(i) Ca(g) → Ca²⁺(g) + 2e^–
Answer:
Endothermic (Ionisation enthalpy is required)

(ii) O(g) + e^– → O^–(g) .
Answer:
Exothermic (first electron affinity-energy is released)

(iii) N^2-(g) + e- → N^3-(g).
Answer:
Endothermic (higher electron affinities are required).

Question 15.
Calculate Δr G^θ for the conversion of oxygen to ozone, \(\frac{3}{2}\)O₂(g) → O₃(g) at 298 K, if K_p for this conversion is 2.47 × 10^-29
Answer:
Δ_r G^θ = – 2.303RT log Kp
and R = 8.314 JK^-1 mol^-1
∴ Δ_r G^θ = – 2.303 × 8.314 × 298 log 2.47 × 10^-29
= 163000 j mol^-1 = 163 kJ mol^-1.

Question 16.
Find the value of the equilibrium constant for the following conversion reaction at 298 K.

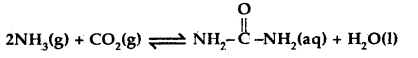
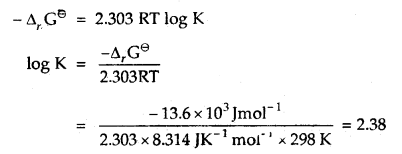
Δ_r G^θ = – 13.6 kJ mol^-1.
Answer:
-Δ_r G^θ = 2.303 RT log K

Question 17.
At 60°C, N₂O₄ is 50% dissociated. Calculate Δ_r G^θ this temperature and at one atmospheric pressure.
Answer:
N₂O₄(g) ⇌ 2NO₂(g)
If N₂O₄ is 50% dissociated, the mole fraction of both the substances are given by

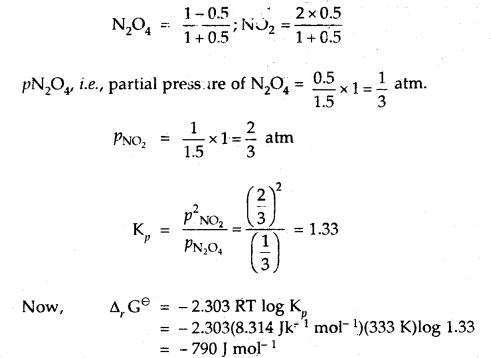
Question 18.
Calculate the heat released when 0.5 moles of the nitric acid solution is mixed with 0.2 moles of potassium hydroxide solution.
Answer:
HNO₃ is a strong acid and KOH is a strong base. Therefore, both are completely ionized in water. The net reaction is

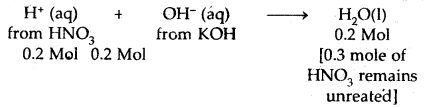
∴ Heat evolved = – 57.1 × 0.2 = – 11.42 kJ.

Question 19.
Define Hess’s Law of Constant Heat Summation.
Answer:
The enthalpy change for a reaction remains the same whether it proceeds in one step or in series of steps all’ measurements being done under similar conditions of temperature.

This law is a corollary from I Law of Thermodynamics.

Question 20.
What are the applications of Hess’s Law of constant heat summation?
Answer:

1. It helps to calculate the enthalpies of formation of those compounds which Cannot be determined experimentally.
2. It helps to determine the enthalpy of allotropic transformations like C(graphite) → C (diamond).
3. It helps to calculate the enthalpy of hydration.

Question 21.
Calculate the maximum work obtained when 0.75 mol of an ideal gas expands isothermally and reversible at 27°C from a volume of 15 L to 25 L.
Answer:
For an isothermal reversible expansion of an ideal gas
w = – nRT log \(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\) = – 2.303 nRT log \(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\)

Putting n = 0.75 mol; V₁ = 15 L; V₂ = 25 L, T = 27 + 273 = 300 K R = 8.314 JK^-1 mol^-1.
w = – 2.303 × 0.75 × 8.314 × 300 log \(\frac{25}{15}\)
= – 955.5 J.

Question 22.
What are heat capacities at constant volume and constant pressure? What is the relationship between them?
Answer:
Heat capacity at constant volume (C_v): Heat supplied to a system to raise its temperature through 1°C keeping the volume of the system constant is called its heat capacity at constant volume (C_v).

Heat capacity at constant pressure (C_p): Heat supplied to a system to raise its temperature through 1°C keeping the external pressure constant is called its heat capacity at constant pressure (C_p).

Relationship between C_p and C_v: C_p – C_v = R.

Question 23.
Explain what do you mean by a reversible process.
Answer:
A process or a change is said to be reversible if it can be reversed at any moment by an infinitesimal change. It proceeds infinitesimally slowly by a series of equilibrium states such that the system and surroundings are always in near equilibrium with each other.

Question 24.
Two liters of an ideal gas at a pressure of 10 atm expands isothermally into a vacuum until its. total volume is 10 liters. How much heat is absorbed and how much work is done in the expansion?
Answer:
We have q = – w: pext(10 – 2) = 0 × 8 = 0
No. work is done; No heat is absorbed.

Question 25.
Define (i) Molar enthalpy of fusion
Answer:
The enthalpy change that accompanies the melting of one mole of a solid substance at its melting point is called the articular enthalpy of fusion.

(ii) Molar enthalpy of vaporisation.
Answer:
The amount of heat required to vaporize one mole of a liquid at constant temperature and under standard pressure (1 bar) is called molar enthalpy of vaporization.

Question 26.
How will you arrive at the relationship q_p = q_v + Δn_gRT?
Answer:
Enthalpy change ΔH = q_p; where q_p = heat change at constant pressure,
Internal energy change ΔU = q_v; where q_v = heat change at. constant volume.

Now ΔH = ΔU + PΔV
For ideal gases PV = nRT
∴ ΔH = ΔU + (PV₂ – PV₁)
= ΔU + P(V₂ – V₁) = ΔU + (n₂RT – n₁RT)
= ΔU + RT(n₂ – n₁) = ΔU + Δn_gRT
or
q_p = q_v + Δn_gRT

Question 27.
Define
(i) Specific heat capacity
Answer:
Specific heat capacity: It is the amount of heat required to raise the temperature of 1 gram of the substance through 1°C.

(ii) molar heat capacity.
Answer:
Molar heat capacity: It is the amount of heat required to raise the temperature of one mole of the substance through 1 °C.

Question 28.
Derive the relationship C_p – C_v = R.
Answer:

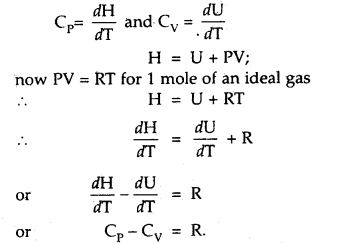
Question 28.
Derive the expression -ΔG = w non-expansion
Answer:
From I law of thermodynamics

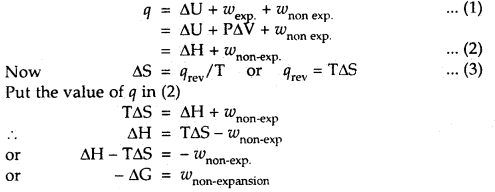
Question 29.
How does the sign of G help in predicting the spontaneity/non-spontaneity of a process?
Answer:

1. IF ΔG is negative, the process is spontaneous.
2. If ΔG = O, the process does not occur and the system is in equilibrium.
3. If ΔG is positive, the process does not proceed in the forward direction.

Question 30.
An exothermic reaction A B is spontaneous in the backward direction. What will be the sign of ΔS for the forward direction?
Answer:
The backward reaction will be endothermic. Thus, the energy factor opposes the backward reaction., As the backward reaction is spontaneous, the randomness factor must favor i.e., ΔS will be positive for the backward reaction or it will be negative for the forward direction.

Thermodynamics Important Extra Questions Long Answer Type

Question 1.
Define
(i) Standard enthalpy of formation.
Answer:
Standard enthalpy of formation: The heat change accompanying the formation of 1 mole df a substance from its elements in their most stable state of aggregation is called its standard enthalpy of formation.
H₂(g) + \(\frac{1}{2}\)O₂(g) H₂O(l); Δ_f He = 285.8 kJ mol^-1

(ii) Standard enthalpy of combustion
Answer:
Standard enthalpy of combustion: It is the heat change accompanying the complete combustion or burning of one mole of a substance in its standard state in excess of air or oxygen.
C₄H₁₀(g) + \(\frac{13}{2}\)O₂(g) → 4CO₂(g) + 5H₂O(1); ΔH^θ = – 2658.0 kJ mol^-1.

(iii) Enthalpy of atomization
Answer:
Enthalpy of atomization: It is defined as the enthalpy change accompanying the breaking of one mole of a substance completely into its atoms in the gas phase.
H₂(g) → 2H(g) Δ_cHe = 435.0 kJ mol^-1

(iv) Enthalpy of solution
Answer:
Enthalpy of solution: It is defined as the heat change when one mole of a substance dissolves in a specified amount of the solvent. The enthalpy of solution at infinite dilution is the enthalpy change observed on dissolving 2 moles of the substance in an infinite amount of the solvent.

(v) Lattice enthalpy
Answer:
Lattice Enthalpy: The lattice enthalpy of an ionic compound is the enthalpy change that occurs when one mole of an ionic compound dissociates into its ions in a gaseous state.

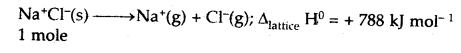
(vi) Thermochemical equation.
Answer:
Thermochemical Equation: A balanced chemical equation together with the value of its A^H is called a thermochemical equation.

The above equation describes the combustion of liquid ethanol. The negative sign indicates that tills are an exothermic reaction. We specify the physical state along with the allotropic state of the substance in a thermochemical equation.

Thermodynamics Important Extra Questions Numerical Problems

Question 1.
For the equilibrium PCl₅(g) ⇌ PCl₃(g) + Cl₂(g) at 298 K, K_c = 1.8 × 10^-7. What is ΔG° for the reaction? (R = 8.314 JK^-1 mol^-1).
Answer:

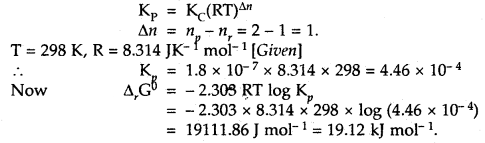
Question 2.
Calculate the equilibrium constant, K, for the following reaction at 400 K?
2NOCl(g) ⇌ 2NO(g) + Cl₂(g)
Given that Δ_rH° = 80.0 kJ mol^-1 and Δ_rS° = 120 JK^-1 mol^-1.
Answer:

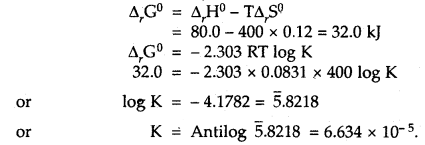
Question 3.
Calculate the standard entropy change for the reaction X ⇌ Y if the value of ΔH° = 28.40 kJ and equilibrium constant is 1.8 × 10^-7 at 298 K and Δ_rG° = 38.484 kJ.
Answer:

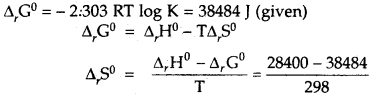
= -33.8 JK^-1 mol^-1

Question 4.
Calculate the enthalpy of formation of methane, given that the enthalpies of combustion of methane, graphite, and hydrogen are 890.2 kJ, 393.4 kJ, and 285.7 kJ mol^-1 respectively.
Answer:

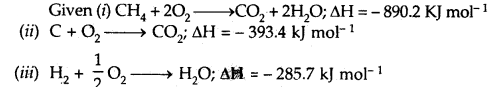
Multiply equation (iii) by 2, add it to equation (ii) and subtract equation (i) from their sum
C + 2H₂ → CH₄ .
ΔH = – 393.4 + 2(-285.7) – (-890.2)
= – 74.6 kJ mol^-1
Hence the heat of formation of methane (CH₄) is
Δ_fH = – 74.6 kJ mol^-1.

Question 5.
CO is allowed to expand isothermally and reversibly from 10 m³ to 20 m³ at 300 K and work obtained is 4.75 KJ. Calculate the number of moles of carbon monoxide (CO). R = 8.314 JK^-1 mol^-1.
Answer:

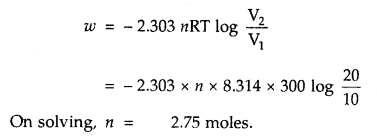
Question 6.
Two moles of an ideal gas initially at 27°C and one atm pressure are compressed isothermally and reversible till the final pressure of the gas is 10 atm. Calculate q, w, and AU for the process.
Answer:
Here n = 2; p₁ = 1 atm; P₂ = 10 atm; T = 300 K
w = 2.303 nRT log \(\frac{\mathrm{P}_{2}}{\mathrm{P}_{1}}\)
= 2.303 × 2 × 8.314 JK mol^-1 × 300 K × log \(\frac{10}{1}\)
= 11488 J .

For isothermal compression of ideal gas
ΔU = 0
Further, ΔU = q + w
∴ q = -w = 11488 J.

Question 7.
The heat of combustion of benzene in a bomb calorimeter (i.e. at constant volume) was found to be 3263.9 kJ mol^-1 at 25°C. Calculate the heat of combustion of benzene at constant pressure.
Answer:
The given reaction is
C₆H₆(l) + \(\frac{15}{2}\) O₂(g) → 6CO₂(g) + 3H₂O(l)
C₆H₆ is a liquid and H20 is a liquid at 25°C.

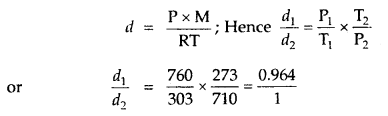
Question 8.
When 0.532 g of benzene (C₆H₆) with boiling point 353 K is burnt with an excess of O₂ in a calorimeter, 22.3 kJ of heat is given out. Calculate ΔH for the combustion process (R = 8.31 JK^-1 mol^-1)
Answer:

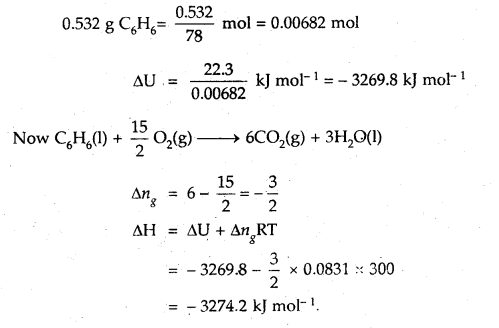
Question 9.
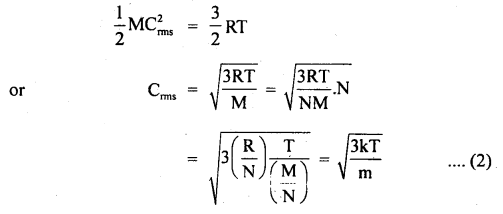
Specific heat of an elementary gas is found to be 0.313 Jat constant volume. If the molar mass of the gas is 40 g mol^-1, what is the atomicity of the gas? R = 8.31 JK^-1 mol^-1.
Answer:

Question 10.
Calculate the energy needed to raise the temperature of 10.0 g of iron from 25° C to 500°C if the specific heat of iron is 0.45 J (0°C)^-1g^-1.
Answer:
Energy needed (q) = m × C × ΔT
= 10.0 × 0.45 × (500 – 25) J
= 2137.5 J

Question 11.
Calculate the enthalpy of formation of carbon disulfide given that the enthalpy of combustion of it is 110.2 kJ mol^-1 and those of sulfur and carbon are 297.4 kJ and 394.5 kJ/g atoms respectively.
Answer:
Our aim is C(s) + 2S(s) → CS₂(l); ΔH =?
Given (i) CS₂(l) + 3O₂(g) → CO₂(g) + 2SO₂(g); ΔH = – 110.2 kJ mol^-1
(ii) S(s) + O₂(g) → SO₂(g); ΔH = – 297.4 kj mol^-1
(iii) C(s) + O₂(g) → CO₂(g); ΔH= – 394.5 kj mol^-1

Add (iii) + 2(ii) and subtract (i), it gives, on rearranging
C(s) + 2S(s) → CS₂(l);
ΔH = (- 394.5) +- 2(- 297.4) – (- 110.2)
= -879.1 kj mol^-1

Thus the enthalpy of formation of CS₂ = – 879.1 kJ mol^-1

Question 12.
There are two crystalline forms of PbO; one is yellow and the other is red. The standard enthalpies of formation of these two forms are – 217.3 and – 219.0 kJ mol^-1 respectively. Calculate the enthalpy change for the solid-solid phase transition:
PbO (yellow) → PbO(red)
Answer:
Our aim is PbO (yellow) → PbO (rpd); ΔH =?
Given (i) PbO(s) + \(\frac{1}{2}\)02(g) ) → PbO (yellow); ΔH = – 217.3 kJ mol^-1
(ii) Pb(s) + \(\frac{1}{2}\)O2(g) ) → PbO(red); ΔH = —219.0 kJ mol^-1

Subtracting (1) from (ii), we get
PbO (yellow) → PbO(red); ΔH =- 219.0 – (- 2173) = – 1.7 kJ mol^-1.

Question 13.
The thermite reaction used for welding of metals involves the reaction 2Al (s) + Fe₂O₃(s) → Al₂O₃(s) + 2Fe(s)
What is Δ_r, H° at 25°C for this reaction? Given that the standard heats of formation of Al₂O₃ and Fe₂O₃ are – 1675.7 k J and – 828.4 kJ mol^-1 respectively.
Answer:
Our aim is 2Al(s) + Fe₂O₃(s) → Al₂O₃(s) + 2Fe(s); Δ_rH° =?

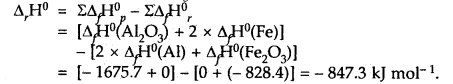
Question 14.
Calculate the bond enthalpy of HCI. Given that the bond enthalpies of H₂ and Cl are 430 and 242 kJ mol^-1 respectively and for HCI is -91 kJ mol^-1.
Answer:

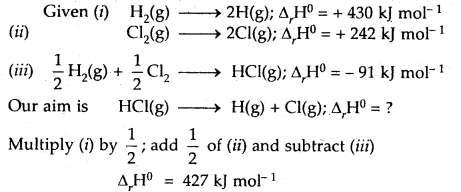
Question 15.
CaIculat the enthalpy of hydrogenation of C₂H₂(g) to C₂H₄(g). Given bond energies: C—H = 414.50 kJ mol^-1; C≡C is 827.6 kJ mol^-1, C=C is 606.0 kJ mol^-1; H—H = 430.5 kJ mol^-1.
Answer:

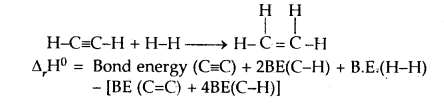
= [827.6 + 2 × 414.0 + 430.5] – [606.0 + 4 × 414.0]
= 175.9 kJ mol^-1.

Question 16.
The entropy change for the vaporization of water is 109 JK^-1 mol^-1. Calculate the enthalpy change for the vaporization of water at 373 K.
Answer:
Δvap H = TΔvap S
= 373 × 10⁹ = 40657 Jmol^-1
= 40.657 kJ mol^-1

Question 17.
Enthalpy and entropy changes of a reaction are 40.63 kJ mol^-1 and 108.8 JK^-1 mol^-1 respectively. Predict the feasibility of the reaction at 27°C.
Answer:
ΔH = 40.63 kJ mol^-1 = 40630 Jmol^-1
ΔS = 108.8 JK^-1 mol^-1
T = 27°C =27 + 273 = 300 K
Now ΔG = ΔH – TΔS
= 40630 – 3 × 108.8 = 7990 J mol^-1

Since AG comes out to be positive (i.e., ΔG > 0), the reaction is not feasible at 27°C in the forward direction.

Question 18.
At 0°C ice and water are in equilibrium and ×H = 6.0 kJ mol^-1 for the process H₂O(s) → H₂O(l). What will be ΔS and
ΔG for the conversion of ice to liquid water.?
Answer:
Since the given process is in equilibrium
ΔG = 0
∴ from the equation ΔG = ΔH – TΔS
ΔH becomes = TΔS

∴ ΔS = \(\frac{6000 \mathrm{~J} \mathrm{~mol}^{-1}}{273 \mathrm{~K}}\) = 21.98 JK^-1 mol^-1.

Question 19.
Calculate the standard- free energy for the reaction
4NH₃(g) + 5O₂(g) → 4NO(g) + 6H₂O(l)
Given that the standard free energies of formation (Δ_fG°) for NH₃(g), NO(g), H₂O(l) are – 16.8, + 86.7, and – 237.2 kJ mol^-1 respectively. Predict the feasibility of the above reaction at the standard state.
Answer:
Given Δ_fG°(NH₃) = – 16.8 kJ mol^-1, Δ_fG°(NO) = + 86.7 kj mol^-1; Δ_fG°(H₂O) = – 237.2 kJ mol^-1

= – [4 × ΔfG°(NH3) + 5 × ΔfG°(O2)]
= [4 × 86.7 + 6(- 237.2)] – [4 × (- 16.8) + 5 × 0]
= – 1009.2 kJ
Since Δ_rG° is negative, the reaction is feasible.

Question 20.
The value of K for the water gas reaction
CO + H₂O ⇌ CO₂ + H₂ is 1.06 × 10⁵ at 25°C. Calculate the standard free energy change for the reaction at 25°C.
Answer:
Δ_rG° = – 2.303 RT log K
= – 2.303 × 8.314 × 298 × log (1.06 × 10⁵)
On solving, Δ_rG° = – 28.38 KJ mol^-1.

Question 21.
Calculate ΔrG° for the conversion of oxygen to ozone. \(\frac{3}{2}\)O2(g) → O3(g) at 298 K. If Kp for the reaction is 2.47 × 10^-29
Answer:
Δ_rG° = – 2.303 RT log K
R = 8.314 JK^-1 mol^-1
∴ Δ_fG° = – 2.303 (8-314 JK^-1 mol^-1) × 298 × (log 2.47 × 10^-29)

On solving
Δ_rG° = 163000 J mol^-1 = 163 kJ mol^-1

Question 22.
Find out the value of the equilibrium constant for the following reaction at 298 K. Standard Gibbs energy change, Δ_rG° at the given temperature is – 13.6 kJ mol^-1.
Answer:
-Δ_rG° = 2.303 RT log K

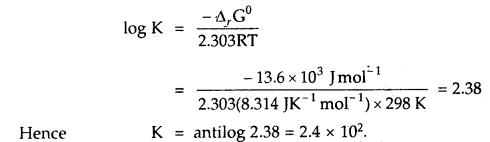
Question 23.
For oxidation of iron, 4Fe(s) + 3O₂(g) → 2Fe₂O₃ (s) entropy change is – 549.4 JK-1 mol-1 at 298 K. Inspite .of negative entropy change of this reaction, why is the reaction spontaneous? (Δ_rH° = -1648 × 103 J mol^-1).
Answer:
The spontaneity of a reaction is determined from ΔS_total
(which is = Δ_sys + Δ_sutu)

Now ΔS_surr = – \(\frac{\Delta_{r} \mathrm{H}^{0}}{\mathrm{~T}}\) at constant pressure
= \(\frac{-1648 \times 10^{3}}{298 \mathrm{~K}}\) J mol^-1 = 5530 JK^-1 mol^-1

Thus total entropy change for the reaction is
Δ_r S_total = 5530 + (- 549.4) = 4980.6 JK^-1 mol^-1.
Since the total entropy change is positive, therefore, the above reaction is spontaneous.

Question 24.
A swimmer coming from a pool is covered with a film of water weighing about 18 g. How much heat must be supplied to evaporate this water at 298 K? Calculate the internal energy of vaporization at 100°C. AvapH° for water.
Answer:

No. of moles in 18 g H₂O(l) = \(\frac{18 \mathrm{~g}}{18 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 1 mol.
Δ_vap U = Δ_vap H° – pΔV = Δ_vapH – Δn_g RT (assuming steam behaving as an ideal gas)
Δ_vap H° – Δn_g RT = 40.66 kJ mol^-1 – (1)(8.314 JK^-1 mol^-1)(373 K) (10^-3 kJ) ,
∴ Δ_vap U° = 40.66 kJ mol^-1 – 3.10 kJ mol^-1 = 37.56 kJ mol^-1

Question 25.
1 g or graphite is burnt in a bomb calorimeter in excess of oxygen at 298 K and 1 atm pressure according to the reaction
C(graphite) + O₂(g) → CO₂(g). During the reaction, the temperature rises from 298 to 299 K. If the heat, the capacity of the bomb calorimeter is 20.7 kJ K^-1 what is the enthalpy change for the above reaction at 298 K and 1. atm?
Answer:
q = Heat change = C_v × ΔT, where q is the heat absorbed by the calorimeter.
The quantity of heat from the reaction will have the same magnitude, but opposite sign, because heat lost by the system (reaction mixture) is equal to the heat gained by the calorimeter.
∴ q = – C_v × ΔT = – 20.7 kJ K^-1 × (299 – 298) K
= -20.7kJ.

Here, negative sign indicates the exothermic nature of the reaction.
Thus, ΔU for the combustion of 1 g of graphite = – 20.7 kJ K^-1 For combustion of 1 mol of graphite
= – \(\frac{12.0 \times(-20.7)}{1}\) = – 2.48 × 10² kJ mol^-1

Since Δng_g = 0
∴ ΔH = ΔU = – 2.48 × 10² kJ mol^-1.

NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry

These Solutions are part of NCERT Solutions for Class 11 Chemistry. Here we have given NCERT Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry.

Question 1.
Calculate the molecular mass of the following :
(i) H₂O (ii) CO₂ (iii) CH₄
Answer:
(i) Molecular mass of H₂O : 2 × 1 + 1 × 16 = 18u
(ii) Molecular mass of CO₂ : 1 × 12 + 2× 16 = 44 u
(iii) Molecular mass of CH₄ : 12 + 4 × 1 = 16 u

The theoretical yield calculator will tell you how many grams of product each reagent can produce, if fully consumed with no byproducts.

Question 2.
Calculate the mass percent of different elements present in sodium sulphate (Na₂SO₄).
Answer:
Molecular mass of Na₂SO₄ = 2 × Atomic mass of Na + Atomic mass of S + 4 × Atomic mass of O
= 2 × 23 + 32 + 4 × 16 = 46 + 32 + 64 = 142 u.
The percentage of different elements present can be calculated as :

Question 3.
Determine the empirical formula of an oxide of iron which has 69-9% iron and 30-1% oxygen by mass.
Answer:
Step I. Calculation of simplest whole number ratios of the elements

The simplest whole number ratios of the different elements are : Fe : O : : 2 : 3
Step II. Writing the empirical formula of the compound.
The empirical formula of the compound = Fe₂CO₃.

Illustration about Set line Chemical formula Calculator, Electrical panel and Light bulb with concept of idea. Color circle button.

Question 4.
Calculate the amount of carbon dioxide that could be produced when
(i) 1 mole of carbon is burnt in air.
(ii) 1 mole of carbon is burnt in 16 g of dioxygen.
(iii) 2 moles of carbon are burnt in 16 g of dioxygen.
Answer:
The chemical equation for the combustion of carbon in dioxygen present in air is :

(i) When 1 mole of carbon is burnt in air
1 mole of carbon will form C0₂ = 1 mol = 44 g
(ii) When 1 mole of carbon is burnt in 16 g of dioxygen
For 1 mole of carbon, dioxygen required = 32 g = 1 mol
But the mass of dioxygen available = 16 g = 1/2 mol .
This means that dioxygen is in limited amount or-it is the limiting reactant.
Since dioxygen and carbon react in the same ratio, therefore mass of CO₂ formed = \(\frac { 1 }{ 2 } \) mol = 22 g
(iii) When 2 moles of carbon are burnt in 16 g of dioxygen
For 2 moles of carbon, dioxygen required = 64 g = 2 mol
But the mass of dioxygen available = 16 g =  \(\frac { 1 }{ 2 } \) mol
This means that dioxygen is in limited amount or it is the limiting reactant.
∴ Mass of C0₂ formed =\(\frac { 1 }{ 2 } \) mol = 22 g

Question 5.
Calculate the mass of sodium acetate (CH3COONa) required to make 500 mL of 0-375 molar aqueous solution. Molar mass of sodium acetate is 82.0 g mol^-1.
Answer:

Question 6.
Calculate the concentration of nitric acid in moles per liter in a sample which has a density of 1.41 g mL-1 and the mass percent of nitric acid in it being 69%.
Answer:
Mass percent 69 means that 69 g of HNo₃ are dissolved in 100 g of the solution.
Mass of solution = 100 g Density of solution = 1.41 g mL^-1

Question 7.
How much copper can be obtained from 100 g of copper sulphate (CuSO₄)?
Answer:
The molecular mass of CuSO₄ = Atomic mass of Cu + Atomic mass of S + 4 x Atomic mass of O
= 63.5 + 32 + 4 × 16
= 159.5 u
Gram molecular mass of CuSO₄ = 159.5 g
Now, 159-5 g of CuSO₄ have Cu = 63.5 g
∴ 100 g of CuSO₄ have Cu = (63.5 g) × \(\frac { (100 g) }{ (159.5 g) } \) = 39.81 g

Question 8.
Determine the molecular formula of an oxide of iron in which the mass percent of iron and oxygen are 69.9 and 30.1 respectively.
Answer:
The empirical formula of the oxide of iron = Fe₂O₃
(For details, refer to No. 3)
Molecular formula of the oxide of iron = n × Empirical formula
= 1 × (Fe₂O₃)
= Fe₂O₃
(Since there is no common factor in Fe₂O₃, therefore n = 1).

Question 9.
Calculate the average atomic mass of chlorine from the following data: Isotope % Natural Abundance Atomic mass

Answer:

Question 10.
In three moles of ethane (C₂H₆), calculate the following:
(i) No. of moles of carbon atoms
(ii) No. of moles of hydrogen atoms No. of molecules of ethane.
Answer:
(i) 1 mole of C₂H₆ has moles of carbon atoms= 2 moles
3 moles of C₂H₆ have moles of carbon atoms= 2 × 3 = 6 moles
(ii) 1 mole of C₂H₆ has moles of hydrogen atoms = 6 moles
3 moles of C₂H₆ have moles of hydrogen atoms = 6 × 3 = 18 moles
(iii) 1 mole of C₂H₆ has molecules = 6.022 × 10²³
3 moles of C₂H₆ have molecules = 6.022 × 10²³ x 3 = 1.81 x 10²⁴

Question 11.
What is the concentration of sugar (C₁₂H₂₂O₁₁) in mol L^-1 of it are dissolved in enough water to make final volume upto 2 L?
Answer:
The concentration in mol L^-1 means molarity (M).
From the available data, it can be calculated as:
Mass of sugar = 20 g
Molar mass of sugar (C₁₂H₂₂o₁₁) = 12 × 12 + 22 × 1 + 11 × 16 = 342 g mol^-1
Volume of solution in litre = 2 L

Question 12.
If the density of methanol is 0.793 kg L^-1, what is its volume needed for making 2.5 L of its 0.25 M solution?
Answer:
Step I. Calculation of the mass of methanol (CH₃OH)
Molar mass of methanol (CH₃OH) =12 + 4×1 + 16 = 32 g mol^-1
Molarity of solution = 0.25 M = 0.25 mol L^-1
Volume of solution = 2.5 L

Step II. Calculation of volume of methanol
Mass of methanol = 20 g = 0-002 kg
Density of methanol = 0-793 kg L^-1

Question 13.
The pressure is determined as force per unit area of the surface. The SI unit of pressure, pascal is as shown below:
IPa = 1 Nm^-2
If the mass of air at sea level is 1034 g, calculate the pressure in pascal.
Answer:

Question 14.
What is the SI unit of mass? How is it defined?
Answer:
Kilogram. It is equal to the mass of the prototype of the kilogram. It is in fact, the mass of a platinum block stored at the International Bureau of Weights and Measurements in France.

Question 15.
Match the following prefixes with their multiples

Answer:
After matching:
micro = 10^-6
deca = 10
mega = 10⁶
giga = 10⁹
femto = 10^-15

Question 16.
What do you understand by significant figures?
Answer:
We have seen that every measurement done in the laboratory involves the same error or uncertainty depending upon the limitation of the measuring instrument. In order to report scientific data, the term ‘significant figures’ has been used. According to this, all digits repotted in a given data are certain except the last one which is uncertain or doubtful. For example, let us suppose that the reading as reported by a measuring scale is 11-64. It has four digits in all. Out of the 1, 1, and 6 are certain digits while the last digit ‘4’ is uncertain. Thus, the number may be reported as follows :

Thus, the significant figures in any number are all certain digits plus one doubtful digit.
It may be noted all digits reported in a number are significant. However, only the last digit is uncertain while the rest are certain. Thus, the number 11-64 has all four digits as significant figures. Out of the 1, 1 and 6 are certain while 4 has some uncertainty about it.

Question 17.
A sample of drinking water was found to be severely contaminated with chloroform CHCI₃, supposed to be a carcinogen. The level of contamination was 15 ppm (by mass)
(i) Express this in percent by mass.
(ii) Determine the molality of chloroform in the water sample.
Answer:
(i) Calculation of percent by mass
15 ppm level of contamination means that 15 parts or 15 g of chloroform (CHCI₃) are present in 10⁶ parts or 10⁶ g of the sample i.e., water.

(ii) Calculation of molality of the solution
Mass of chloroform = 1.5 x 10^-3 g
Molar mass of chloroform (CHCI₃) = 12 + 1 + (3 × 35.5) = 119.5 g mol^-1
Mass of sample i.e., water = 100 g

Question 18.
following in the scientific notation:
(i) 0.0048
(ii) 234,000
(iii) 8008
(iv) 500.0
(v) 6.0012
Answer:
(i) 4.8 x 10^-3
(ii) 2.34 × 10⁵
(iii) 8.008 × 10³
(iv) 5.000 × 10²
(v) 6.0012 × 10⁰

Question 19.
How many significant figures are present in the following?
(i) 0.0025
(ii) 208
(iii) 5005
(iv) 126,000
(iv) 500.0.
(v) 2.0034
Answer:
(i) 2
(ii) 3
(iii) 4
(iv) 6
(v) 4
(vi) 5

Question 20.
Round up the following upto three significant figures :
(i) 34.216
(ii) 10.4107
(iii) 0.04597
(iv) 2808
Answer:
(i) 34.2
(ii) 10.4
(iii) 0.0460
(iv) 281

Question 21a.
The following data is obtained when dinitrogen and dioxygen react together to form different compounds :

Answer:
By keeping 14 g as the fixed mass of dinitrogen (N₂), the ratios by mass of dioxygen (O₂) combining with 14 g dinitrogen are : 16 : 32 : 16 : 40 or 2 : 4 : 2 : 5. Since this ratio is simple whole number, the data obeys the Law Multiple Proportions.

Question 21b.
Fill in the blanks in the following conversions :
(i) 1 km = ……… mm = ……….. pm
(ii) 1 mg = …….. kg = …………. ng
(iii) 1 mL = ……. L = ………… dm³.
Answer:

Question 22.
If the speed of light is 3.0 x 10⁸ m s^-1, calculate the distance covered by light in 2.00 ns.
Answer:

Question 23.
Identify the limiting reactant if any in the following reaction mixtures ?
A + B → AB₂
(i) 300 atoms of A + 200 molecules of B₂
(ii) 100 atoms of A + 100 molecules of B₂
(iii) 5 moles of A + 2.5 moles of B₂
(iv) 2.5 moles of A + 5 moles of B₂
(v) 2 moles of A + 3 moles of B₂.
Answer:

In the light of the above information, let us find the limiting reactant if any in all the cases
(i) 1 atom of A will react with molecules of B₂ =1
300 atoms of A will react with molecules of B₂ = 300
But the molecules of B₂ actually available = 200
∴B₂ is the limiting reactant.

(ii) 1 atom of A will react with molecules of B₂ = 1
100 atoms of A will react with molecules of B₂ = 100
The molecules of B₂ actually available = 100
∴There is no limiting reactant in this case.

(iii) 1 mole of A will react with moles of B₂ =1
5 moles of A will react with moles of B₂ =5
But the moles of B₂ actually available = 2.5
∴B₂ is the limiting reactant.

(iv) 1 mole of A will react with moles of B₂ =1
2.5 moles of A will react with moles of B₂ = 2.5
But moles of B₂ actually available = 5
This shows that 5 moles of A can react whereas only 2.5 moles of A are actually available.
∴A is the limiting reactant.

(v) 1 mole of A will react with moles of B₂ = 1
2 moles of A will react with moles of B = 2
But the moles of B2 actually available = 3
This shows that 3 moles of A can react whereas only 2 moles of A are actually available.
∴ A is the limiting reactant.

Question 24.
Nitrogen and hydrogen react to form ammonia according to the reaction
N₂ (g) + 3H₂ (g) →2NH₃(g)
If 1000 g of H₂ react with 2000 g of N₂,
(i) will any of the two reactants remain unreacted ? If yes, which one and what would be its mass ?
(ii) Calculate the mass of ammonia (NH₃) which will be formed.
Answer:

According to available data,
28 g of N₂ require H₂ = 6 g
2000 g of N₂ require H₂ = (6g) x \(\frac { 2000 g }{ 28 g }\)=428.6 g
But H₂ actually available = 1000 g
This means that H₂ is in excess and will remain unreacted.
(i) Mass of H₂ that remains unreacted = 1000 – 428.6 = 571.4 g
(ii) Mass of NH₃ formed may be calculated as follows :
6 g of H₂ will form NH₃ = 34 g
428.6 g H₂ will form NH₃ = (34g) x \(\frac { 428.6 g }{ 6.0 g }\) = 2428.8 g

Question 25.
How are 0.50 mol Na₂Co₃ and 0.50 M Na₂Co₃ different ?
Answer:
0.50 mol Na₂CO₃ represent concentration in moles.
0.50 M Na₂CO₃ represent concentration in moles/litre (molarity).

Question 26.
If 10 volumes of dihydrogen react with five volumes of dioxygen gas, how many volumes of water will be produced ?
Answer:

10 volumes of water vapours will be produced.

Question 27.
Convert the following into basic units
(i) 28.7 pm
(ii) 15.15 \xs
(iii) 25365 mg.
Answer:

Question 28.
Which of the following has largest number of atoms ?
(i) 1 g of Au
(ii) lg of Na
(iii) 1 g of Li
(iv) lg of Cl₂
Answer:
(i) 197 g of Au have atoms = 6.022 x 10²³
∴ l g of Au has atoms = 6.022 × 10²³ × \(\frac { 1 g }{ 197g }\) = 3.06 x 10²¹
(ii) 23 g of Na have atoms = 6.022 × 10²³
1 g of Na has atoms = 6 -022 × 10²³ × \(\frac { 1 g }{ 23g }\) = 2.62 x 10²² atoms
(iii) 71 g of Cl₂ have molecules = 6.022 × 10²³
71 g of Cl₂ have atoms = 2 × 6.022 x 10²³
1 g of Cl₂ has atoms = 2 × 6.022 × 10²³ x \(\frac { 1 g }{ 71g }\) = 1.67 × 10²² atoms
Thus, 1 g of lithium (Li) has the largest number of atoms.

Question 29.
Calculate the molarity of a solution of ethanol in water in which mole fraction of ethanol is 0.04.
Answer:

2.31 moles of ethanol are dissolved in 1000 g (or 1000 mL) of water or 1000 mL of the solution. In this case, the volume of solution is considered to be the same as that of the solvent i.e., water. In other words, the solution is regarded as dilute solution,
∴Molarity of solution = 2.31 M

Question 30.
What will be mass of one ¹²C in g ?
Answer:

Question 31.
How many significant figures should be present in the answer of the following calculations ?
(i) \(\frac { 0.2856 x 298.15 x 0.112 }{ 0.5785 }\)
(ii) 5 x 5.364
(iii) 0.0125 + 0-7864 4- 0.0215.
Answer:
(i) The least precise figure (0.112) has 3 significant figures. Therefore, the answer should have three significant figures.
(ii) The second figure (5.364) has 4 significant figures. Therefore, the answer should be reported upto four significant figures. The exact figure (5) is not considered in this case.
(iii) In this case, the least precise figures (0.0125 and 0.0215) have 3 significant figures. Therefore, the answer should be reported upto three significant figures.

Question 32.
Use the data given in the following table to calculate the molar mass of naturally occurring argon.

Answer:
Molar mass of argon is the average molar mass and may be calculated as :

Question 33.
Calculate the number of atoms present in : (i) 52 moles of He (ii) 52 u of He (iii) 52 g of He.
Answer:
(i) 1 mole of He contains atoms = 6.022 × 10²³
52 moles of He contain atoms = 6.022 x 10²³ x 52 = 3-13 × 10²⁵ atoms
(ii) Atomic mass of He = 4 u ; 4 u is the mass of He atoms = 1
52 u is the mass of He atoms = \(\frac { 1 }{ 4 }\) x 52 = 13 atoms
(iii) Gram atomic mass of He = 4 g ; 4 g of He contain atoms = 6.022 × 10²³

Question 34.
A welding fuel gas contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g carbon dioxide, 0.690 g water and no other products. A volume of 10.0 L (measured at NTP) of this welding gas is found to weigh 11.6 g. Calculate (i) empirical formula (ii) molar mass and (iii) molecular formula of the gas.
Answer:
Step I. Calculation of mass percent of carbon and hydrogen.

Step II. Determination of empirical formula of fuel gas.
Empirical formula of the fuel gas = CH.

Step III. Calculation of molecular mass of fuel gas.
10.0 L of the fuel gas at N.T.P. weigh = 11.6 g
22.4 L of the fuel gas at N.T.P. weigh =\(\frac { 11.6 }{ 10.0}\) × 24.4 =25.98 g
Molecular mass of the fuel gas = 25.98 g \(\approx \) 26.0 g = 26 u

Step IV. Calculation of molecular formula of the gas.
Empirical formula mass = 12 + 1 = 13 u
Molecular mass = 26 u
n = \(\frac { Molecular mass }{ Empirical formula mass }\) × \(\frac { 126 }{ 13}\) = 2
∴ Molecular formula = n × Empirical formula = 2 × CH = C₂H₂
The molecular formula of fuel gas is C₂H₂ and it is acetylene.

Question .35.
Calcium carbonate reacts with aqueous HCl to give CaCl₂ and Co₂ according to the reaction :
CaCo₃ (s) + 2HCl (aq) + CaCl₂ (aq) + Co₂ (g) + H₂o (l)
What mass of CaCo₃ is required to react completely with 25 mL of 0.75 M HCl ?
Answer:

Question 36.
Chlorine is prepared in the laboratory by treating manganese dioxide (Mno₂) with aqueous hydrochloric acid according to the reaction :
4HCl(aq) + MnO₂(s) → MnCl₂(aq) + Cl₂(g) + 2H₂O(l)
How many grams of HCl react with 5.0 g of manganese dioxide ?
Answer:

We hope the NCERT Solutions for Class 11 Chemistry at Work Chapter 1 Some Basic Concepts of Chemistry, help you. If you have any query regarding NCERT Solutions for Class 11 Chemistry at Work Chapter 1 Some Basic Concepts of Chemistry, drop a comment below and we will get back to you at the earliest.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 13 Kinetic Theory. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 13 Important Extra Questions Kinetic Theory

Kinetic Theory Important Extra Questions Very Short Answer Type

Question 1.
What does gas constant R signify? What is its value?
Answer:
The universal gas constant (R) signifies the work done by (or on) a gas per mole per kelvin. Its value is 8.31 J mol^-1 K

Question 2.
What is the nature of the curve obtained when:
(a) Pressure versus reciprocal volume is plotted for an ideal gas at a constant temperature.
Answer:
It is a straight line.

(b) Volume of an ideal gas is plotted against its absolute temperature at constant pressure.
Answer:
It is a straight line.

Question 3.
The graph shows the variation of the product of PV with the pressure of the constant mass of three gases A, B and C. If all the changes are at a constant temperature, then which of the three gases is an ideal gas? Why?

Answer:
A is an ideal gas because PV is constant at constant temperature for an ideal gas.

Question 4.
On the basis of Charle’s law, what is the minimum possible temperature?
Answer:
– 273.15°C.

Question 5.
What would be the ratio of initial and final pressures if the masses of all the molecules of a gas are halved and their speeds are doubled?
Answer:
1: 2 (∵ P = \(\frac{1}{3} \frac{\mathrm{mn}}{\mathrm{V}}\)C²)

Question 6.
Water solidifies into ice at 273 K. What happens to the K.E. of water molecules?
Answer:
It is partly converted into the binding energy of ice.

Question 7.
Name three gas laws that can be obtained from the gas equation.
Answer:

1. Boyle’s law
2. Charle’s law
3. Gay Lussac’s law.

Question 8.
What is the average velocity of the molecules of a gas in equilibrium?
Answer:
Zero.

An online Charles law calculator determines the value of initial temperature, final temperature, initial volume, final volume, pressure, ext…

Question 9.
A vessel is filled with a mixture of two different gases. Will the mean kinetic energies per molecule of both gases be equal? Why?
Answer:
Yes. This is because the mean K.E. per molecule i.e. \(\frac{3}{2}\) kT depends only upon the temperature.

Question 10.
Four molecules of a gas are having speeds, v₁, v₂, v₃ and v₄.
(a) What is their average speed?
Answer:
V_av = \(\frac{v_{1}+v_{2}+v_{3}+v_{4}}{4}\)

(b) What is the r.m.s. speed?
Answer:
V_rms = \(\sqrt{\frac{v_{1}^{2}+v_{2}^{2}+v_{3}^{2}+v_{4}^{2}}{4}}\)

Question 11.
The density of a gas is doubled, keeping all other factors unchanged. What will be the effect on the pressure of the gas?
Answer:
It will be doubled. (∵ P ∝ ρ if other factors are constant).

Question 12.
What is the average translational K.E. of an ideal gas molecule at a temperature T?
Answer:
\(\frac{3}{2}\) kT, where k is Boltzmann Constant.

Question 13.
Define the mean free path of a molecule.
Answer:
It is defined as the average distance travelled by a molecule between two successive collisions.

Question 14.
At what temperature, Charle’s law breaks down?
Answer:
At very low temperature, Charle’s law breaks down.

Question 15.
A container has an equal number of molecules of hydrogen and carbon dioxide. If a fine hole is made in the container, then which of the two gases shall leak out rapidly?
Answer:
Hydrogen would leak faster as r.m.s. speed of hydrogen is greater than the r.m.s. speed of CO₂.

Question 16.
Two different gases have the same temperature. Can we conclude that the r.m.s? velocities of the gas molecules are also the same? Why?
Answer:
No. If temperature is same, then \(\frac{3}{2}\) kT is same. Also \(\frac{1}{2}\) mC² is same. But m is different for different gases. C will be different.

Question 17.
A gas enclosed in a container is heated up. What is the effect on pressure?
Answer:
The pressure of the gas increases.

Question 18.
What is an ideal gas?
Answer:
It is a gas in which intermolecular forces are absent and it obeys gas laws.

Question 19.
Define absolute zero.
Answer:
It is defined as the temperature at which all molecular motions cease.

Question 20.
What do you understand by the term ‘Collision frequency’?
Answer:
It is the number of collisions suffered by a molecule in one second.

Question 21.
What do you understand by the term ‘mean free path’ of a molecule?
Answer:
It is the average distance travelled by the molecule between two successive collisions.

Question 22.
Mention two conditions when real gases obey the ideal gas equation PV = RT?
Answer:
Low pressure and high temperature.

Question 23.
Comment on the use of water as a coolant.
Answer:
Since water has a high value of specific heat so it can be used as a coolant.

Question 24.
Do Water and ice have the same specific heats? Why water bottles are used for fomentation?
Answer:
No. For water C = 1 cal g^-1 °C^-1 for ice, C = 0.5 cal g^-1°C^-1. It is because water has a high value of specific heat.

Question 25.
(a) What is the value of γ for a monoatomic and a diatomic gas?
Answer:
γ is 1.67 and 1.4 for monoatomic and diatomic gas respectively.

(b) Does the value of y depend upon the atomicity of the gas?
Answer:
Yes.

Question 26.
Which of the two has larger specific heat-monoatomic or diatomic gas at room temperature?
Answer:
Diatomic gas has more specific heat than a monoatomic gas e.g. Molar specific heat at constant volume is \(\frac{5}{2}\)R for monoatomic gas and \(\frac{5}{2}\)R for diatomic gas.

Question 27.
What is the effect on the pressure of an if it is compressed at constant temperature?
Answer:
Applying Boyle’s law, we find that the pressure increases.

Question 28.
What is the volume of a gas at absolute zero of temperature?
Answer:
Zero.

Question 29.
Why the pressure of a gas enclosed in a container increases on heating?
Answer:
This is because the pressure of a gas is proportional to the absolute ‘ temperature of the gas if V is constant.

Question 30.
The number of molecules in a container is doubled. What will be the effect on the r.m.s? speed of Slit molecules?
Answer:
No effect.

Question 31.
What will be the effect on K.E. and pressure of the gas in the above quation?
Answer:
Both will be doubled.

Question 32.
Does real gases obey the gas equation, PV = nRT.
Answer:
No.

Question 33.
On what factors does the internal energy of a real gas depend?
Answer:
It depends upon the temperature, pressure and volume of the gas.

Question 34.
What is the pressure of an ideal gas at absolute zero i.e. 0 K or – 273°C.
Answer:
Zero.

Question 35.
What do NTP and STP mean?
Answer:
They refer to a temperature of 273 K or 0°C and 1 atmospheric pressure.

Question 36.
What is the internal energy or molecular energy of an ideal gas at absolute zero?
Answer:
Zero.

Question 37.
Name the temperature at which all real gases get liquified?
Answer:
All real gases get liquified before reaching absolute zero.

Question 38.
Is the internal energy of the real gases sera at the absolute temperature?
Answer:
No.

Kinetic Theory Important Extra Questions Short Answer Type

Question 1.
Why cooling is caused by evaporation?
Answer:
Evaporation occurs on account of faster molecules escaping from the surface of the liquid. The liquid is therefore left with molecules having lower speeds. The decrease in the average speed of molecules results in lowering the temperature and hence cooling is caused.

Question 2.
On reducing the volume of the gas at a constant temperature, the pressure of the gas increases. Explain on the basis of the kinetic theory of gases.
Answer:
On reducing the volume, the space for the given number of molecules of the gas decreases i.e. no. of molecules per unit volume increases. As a result of which more molecules collide with the walls of the vessel per second and hence a larger momentum is transferred to the walls per second. Due to which the pressure of gas increases.

Question 3.
Why temperature less than absolute zero is not possible?
Answer:
According to the kinetic interpretation of temperature, absolute temperature means the kinetic energy of molecules.

As heat is taken out, the temperature falls and hence velocity decreases. At absolute zero, the velocity of the molecules becomes zero i.e. kinetic energy becomes zero. So no more decrease in K.E. is possible, hence temperature cannot fall further.

Question 4.
There are n molecules of a gas in a container. If the number of molecules is increased to 2n, what will be:
(a) the pressure of the gas.
(b) the total energy of the gas.
(c) r.m.s. speed of the gas molecules.
Answer:
(a) We know that
P = \(\frac{1}{3}\)mnC².
where n = no. of molecules per unit volume.
Thus when no. of molecules is increased from n to 2n, no. of molecules per unit volume (n) will increase from n 2n
\(\frac{n}{V}\) to \(\frac{2n}{V}\), hence pressure will become double.

(b) The K.E. of a gas molecule is,
\(\frac{1}{2}\)mC² = \(\frac{3}{2}\)kT
If the no. of molecules is increased from n to 2n. There is no effect on the average K.E. of a gas molecule, but the total energy is doubled.

r.m.s speed of gas is C_rms = \(\sqrt{\frac{3 \mathrm{P}}{\rho}}=\sqrt{\frac{3 \mathrm{P}}{\mathrm{mn}}}\)

When n ¡s increased from n to 2n. both n and P become double and the ratio \(\frac{P}{n}\) remains unchanged. So there will be no effect of increasing the number of molecule from n to 2n on r.m.s. speed of gas molecule.

Question 5.
Equal masses of O₂ and He gases are supplied equal amounts of heat. Which gas will undergo a greater temperature rise and why?
Answer:
Helium is monoatomic while O₂ is diatomic. In the case of helium, the supplied heat has to increase only the translational K.E. of the gas molecules.

On the other hand, in the case of oxygen, the supplied heat has to increase the translations, vibrational and rotational K.E. of gas molecules. Thus helium would undergo a greater temperature rise.

Question 6.
Two bodies of specific heats S₁ and S₂ having the same heat capacities are combined to form a single composite body. What is the specific heat of the composite body?
Answer:
Let m₁ and m₂ be the masses of two bodies having heat capacities S₁ and S₁  respectively.
∴ (m₁ + m₂)S = m₁S₁ + m₂S₂ = m₁S₁ + m₁S₁ = 2m₁S₁

S = \(\frac{2 m_{1} S_{1}}{m_{1}+m_{2}}\).

Also, m₂S₂ = m₁S₁
( ∵ Heat capacities of two bodies are same.)
or
m₂ = \(\frac{\mathrm{m}_{1} \mathrm{~S}_{1}}{\mathrm{~S}_{2}}\)

∴ S = \(\frac{2 \mathrm{~m}_{1} \mathrm{~S}_{1}}{\mathrm{~m}_{1}+\frac{\mathrm{m}_{1} \mathrm{~S}_{1}}{\mathrm{~S}_{2}}}=\frac{2 \mathrm{~S}_{1} \mathrm{~S}_{2}}{\mathrm{~S}_{1}+\mathrm{S}_{2}}\)

Question 7.
Tell the degree of freedom of:
(a) Monoatomic gas moles.
Answer:
A monoatomic gas possesses 3 translational degrees of freedom for each molecule.

(b) Diatomic gas moles.
Answer:
A diatomic gas molecule has 5 degrees of freedom including 3 translational and 2 rotational degrees of freedom.

(c) Polyatomic gas moles.
Answer:
The polyatomic gas molecule has 6 degrees of freedom (3 translational and 3 rotational).

Question 8.
State law of equipartition of energy.
Answer:
It states that in equilibrium, the total energy of the system is divided equally in all possible energy modes with each mode i.e. degree of freedom having an average energy equal to \(\frac{1}{2}\) k_BT.

Question 9.
Explain why it is not possible to increase the temperature of gas while keeping its volume and pressure constant?
Answer:
It is not possible to increase the temperature of a gas keeping volume and pressure constant can be explained as follows:

According to the Kinetic Theory of gases,

( ∵ C² = kT, when k is a constant)
T ∝ PV

Now as T is directly proportional to th^ product of P and V. If P and V are constant, then T is also constant.

Question 10.
A glass of water is stirred and then allowed to stand until the water stops moving. What has happened to the K.E. of the moving water?
Answer:
The K.E. of moving water is dissipated into internal energy. The temperature of water thus increases.

Question 11.
Why the pressure of a gas increases when it is heated up?
Answer:
This is due to the two reasons:

1. The gas molecules move faster than before on heating and so strike the container walls more often.
2. Each impact yields greater momentum to the walls.

Question 12.
R.m.s. velocities of gas molecules are comparable to those of a single bullet, yet a gas takes several seconds to diffuse through a room. Explain why?
Answer:
Gas molecules collide with one another with a very high frequency. Therefore, a molecule moves along a random and long path to go from one point to another. Hence gas takes several seconds to go from one comer of the room to the other.

Question 13.
Calculate the value of the universal gas constant (R).
Answer:
We know that R is given by
R = \(\frac{PV}{T}\)

Now one mole of all gases at S.T.P. occupy 22.4 litrês.
P = 0.76 m of Hg
= 0.76 × 13.6 × 10³ × 9.8
= 1.013 × 10⁵ Nm^-2

V = 22.4 litre
= 22.4 × 10 3m³

T = 273 K .
n = 1

∴ R = \(\frac{1.013 \times 10^{5} \times 22.4}{273}\) × 10^-3
= 8.31 J mol^-1 k^-1

Question 14.
Define and derive an expression for the mean free path.
Answer:
It is defined as the average distance travelled by a gas molecule between two successive collisions. It is denoted by X.

Derivation of Expression – Let us assume that only one molecule is in motion and all other molecules are at rest. ,
Let d = diameter of each molecule.
l = distance travelled by the moving molecule.

The moving molecule will collide with all those molecules whose centres lie inside a volume πd2l.
Let n = no. of molecules per unit volume in the gas.

Now λ = \(\frac{\text { distance travelled }}{\text { no. of collisions }}=\frac{l}{\mathrm{n} \pi \mathrm{d}^{2} l}\)
or
λ = \(\frac{1}{n \pi d^{2}}\) …(1)

In this derivation, we have assumed that all but one molecules are at rest. But this assumption is not correct. All the molecules are in random motion. So the chances of a collision by a molecule are greater.

Thus taking it into account, the mean free path can be shown to be \(\sqrt{2}\) times less than that in equation (1),
∴ λ = \(\frac{1}{\sqrt{2} n \pi d^{2}}\)
which is the required expression.

Question 15.
On what parameters does the λ (mean free path) depends?
Answer:
we know that λ = \(\frac{\mathrm{k} \mathrm{T}}{\sqrt{2} \pi \mathrm{d}^{2} \rho}=\frac{\mathrm{m}}{\sqrt{2} \pi \mathrm{d}^{2} \rho}\)

= \(\frac{1}{\sqrt{2} \pi \mathrm{nd}^{2}}\)
∴ λ depends upon:

1. diameter (d) of the molecule, smaller the ‘d’, larger is the mean free path λ,.
2. λ ∝ T i.e. higher the temperature, larger is the λ.
3. λ ∝ \(\frac{1}{P}\) i.e. smaller the pressure, larger is the λ.
4. λ ∝ \(\frac{1}{ρ}\) i.e. smaller the density (ρ), larger will he the X.
5. λ ∝ \(\frac{1}{n}\) i.e. smaller the number of molecules per unit volume of the gas, larger is the λ.

Question 16.
What causes the Maxwellian distribution of molecular speed?
Answer:
Maxwellian distribution of molecular speed is a statistical phenomenon due to the intermolecular collisions in which the system tends to acquire equilibrium.

Question 17.
Why the pressure of a gas increases on increasing the temperature at constant volume?
Answer:
We know that C_rms ∝ \(\sqrt{T}\).

Thus when T is increased, the root means square velocity of gas molecules also increases, thus they move faster and the number of collisions per second with the walls of the container increase and thus pressure increases.

Question 18.
Explain why the temperature of a gas rises when it is compressed?
Answer:
The work is done against pressure during the compression and the velocity of the individual molecules increases, so their K..E. is increased and thus the temperature of the gas is increased.

Question 19.
What determines the average speeds of the molecules of the gases?
Answer:
The average speed of the molecules of the gases depends upon their mass and temperature.

Question 20.
What is the average velocity of the molecules of an ideal gas? Why?
Answer:
The average velocity of the molecules of an ideal gas is zero because the molecules possess all sorts of velocities in all possible directions. Thus their vector sum and hence average value is zero.

Question 21.
A person putting on wet clothes may catch cold-Why?
Answer:
The water in the clothes evaporates. The heat required for evaporation is taken from the body of the person wearing wet clothes. So due to the cooling of the body, he may catch a cold.

Question 22.
At what temperature the molecular speed of the gas molecules should reduce to zero? Does it really happen? Why?
Answer:
The molecular speed should reduce to zero at absolute zero. But such a situation never arises because all gases liquefy before that temperature is attained.

Question 23.
The temperature of the gas in Kelvin is made 9 times. How does it affect the total K.E., average K.E., r.m.s? velocity and pressure?
Answer:
Total K.E., average K.E. and pressure become 9 times, but the RMS velocity is tripled.

Question 24.
Do diatomic molecules have all types of motions? Explain.
Answer:
No. At very low temperature, they have only translatory r motion. At moderate temperature, they possess both translatory and rotatory motion and at very high temperature, all three types of motions are possible.

Question 25.
Why the molecules of an ideal monoatomic gas have only three degrees of freedom?
Answer:
It is so because the molecules of an ideal gas are point masses, so rotational motions are not significant. Thus it can have only three degrees of freedom corresponding to the translatory motion.

Question 26.
The adiabatic expansion causes a lowering of the temperature of the gas. Why?
Answer:
As the gas expands work needs to be done by the gas. The process being adiabatic, no heat is absorbed by the gas from outside, so the energy for doing work is obtained from the gas itself and hence its temperature falls.

Question 27.
What are the different ways of increasing the number of molecular collisions per unit time against the walls of the vessel containing a gas?
Answer:
The number of collisions per unit time .an be increased in the following ways:

1. By increasing the temperature of the gas.
2. By increasing the number of molecules.
3. By decreasing the volume of the gas,

Question 28.
Two identical cylinders contain helium at 2 atmospheres and argon at 1 atmosphere respectively. If both the gases are filled in one of the cylinders, then:
(a) What would be the pressure?
Answer:
(2 + 1) = 3 atmosphere.

(b) Will the average translational K.E. per molecule of both gases be equal?
Answer:
Yes, because the average translational K.E./molecule (\(\frac{3}{2}\)kT) depends only upon the temperature.

(c) Will the r.m.s. velocities are different?
Answer:
Yes, because of the r.m.s. velocity depends not only upon temperature but also upon the mass.

Question 29.
Why hydrogen escapes more rapidly than oxygen from the earth’s surface?
Answer:
We know that C_rms ∝ \(\frac{1}{\sqrt{\rho}}\)

Also ρ₀ = 16 ρ_H. So C_rms of hydrogen is four times that of oxygen at a given temperature. So the number of hydrogen molecules whose velocity exceeds the escape velocity from earth (11.2 km s^-1) is greater than the no. of oxygen molecules. Thus hydrogen escapes from the earth’s surface more rapidly than oxygen.

Question 30.
When a gas is heated, its molecules move apart. Does it increase the P.E. or K.E. of the molecules? Explain.
Answer:
It increases the K.E. of the molecules. Because on heating, the temperature increases and hence the average velocity of the molecules also increases which increases the K.E.

Question 31.
Distinguish between the terms evaporation, boiling and vaporisation.
Answer:
Evaporation: It is defined as the process of conversion of the liquid to a vapour state at all temperatures and occurs only at the surface of the liquid.

Boiling: It is the process of rapid conversion of the liquid to a vapour state at a definite temperature and occurs throughout the liquid.

Vaporisation: It is the general term for the conversion of liquid to vapour state. It includes both evaporation and boiling.

Kinetic Theory Important Extra Questions Long Answer Type

Question 1.
Derive gas laws from the kinetic theory of gases.
Answer:
(a) Boyle’s law: It states that P ∝ \(\frac{1}{V}\) if T = constant.
Derivation: We know from the kinetic theory of gases that

Here R = constant
If T = constant, then PV = constant
or
P ∝ \(\frac{1}{V}\).

(b) Charles’ law: It states that for a given mass of a gas, the volume of the gas is directly proportional to the absolute temperature of the gas if pressure is constant
i. e. V ∝ T.

Derivation: We know that
PV = \(\frac{1}{3}\)MC2= \(\frac{1}{3}\)mNC2
where N = Avogadro’s no.

Also, we know that mean K..E. of a molecule is

If P = constant, then V ∝ T. Hence proved.

(c) Avogadro’s Hypothesis: It states that equal volumes of all gases contain equal no. molecules if T and P are the same.

Derivation: Consider two gases A and B having n, and n2 as the no. of molecules, C₁ and C₂ are the r.m.s. velocities of these molecules respectively.

According to the kinetic theory of gases,

Also, we know that

Hence proved.

(d) Graham’s law of diffusion of gases: It states that the rate of diffusion of a gas is inversely proportional to the square root of the density of the gas.
Derivation: We know that

Also, we know that r.m.s. velocity is directly proportional to the rate of diffusion (r) of the gas, i.e.

Numerical Problems:

Question 1.
Calculate r.m.s. the velocity of hydrogen at N.T.P. Given the density of hydrogen = 0.09 kg m⁴.
Answer:

Question 2.
Calculate the temperature at which r.m.s. the velocity of the gas molecule is double its value at 27°C, the pressure of the gas remaining the same.
Answer:
Let t be the required temperature = ? and Ct, C27 be the r.m.s. velocities of the gas molecules at t°C and 27°C respectively.
\(\frac{\mathrm{C}_{\mathrm{t}}}{\mathrm{C}_{27}}\) = 2 (given)
Also let M = molecular weight of the gas
Now T = t + 273
and T₂₇ = 27 + 273 = 300 K

∴ Using the relation

Question 3.
Calculate the K.E./mole of a gas at N.T.P. Density of gas at N.T.P. = 0.178 g dm^-3 and molecular weight = 4.
Answer:
Here, ρ = 0.178 g dm^-3
= 0.178 × 10^-3 g cm^-3 (∵ 1 dm³ = 10^-3 cm³)
= 178 × 10^-6 g cm^-3

Volume of 1 mole of gas i.e. 4 g of gas = \(\frac{\text { Mass }}{\text { Density }}\)

Question 4.
Calculate the diameter of a molecule if n = 2.79 × 10²⁵ molecules per m3 and mean free path = 2.2 × 10^-8 m.
Answer:
Here, n = 2.79 × 10²⁵ molecules m^-3
λ = 2.2 × 10^-8 m
d = ?

Using the relation.

Question 5.
Calculate the number of molecules in 1 cm3 of a perfect gas at 27°C and at a pressure of 10 mm ofHg. Mean K.E. of a molecule at 27°C = 4 × 10²⁵ J. ρ_Hg = 13.6 × 103 kg m^-3.
Answer:
Here, K..E. per molecule at 27°C = 4 × 10^-11 J
Let μ = number of molecules in 1 cm³ or 10^-6 m³
∴ Mean K.E. per cm3 = μ × 4 × 10¹¹ J ….(i)
Now K.E. per gram molecule = \(\frac{3}{2}\) RT
for a perfect gas, PV = RT

∴ K.E, per gram molecule = \(\frac{3}{2}\) PV
or
K.E. per cm3 of gas = \(\frac{3}{2}\) PV
P = 10 mm of Hg = 10^-2 m of Hg
= 10^-2 × 13.6 × 10³ × 9.8
= 136 × 9.8 Nm^-2 V
= 1 cm³
= 10^-6 m³

∴ K.E per cm3 of gas = \(\frac{3}{2}\) × 136 × 9.8 × 10⁶
= 1.969 × 10^-3 J ….(ii)

∴ from (i) and (ii) we get
μ × 4 × 10^-11 = 1.969 × 10^-3
or
μ = \(\frac{1.969 \times 10^{-3}}{4 \times 10^{11}}\)
= 4.92 × 10⁷ molecules

Question 6.
Gas at 27°C ¡n a cylinder has a volume of 4 litres and pressure 1oo Nm².
(a) Gas is first compressed at a constant temperature so that the pressure is 150 Nm². Calculate the change in volume.
Answer:
Here, V₁ = 4 litres = 4 × 10^-3 m³
P₁ = 100 Nm^-2
P₂ = 150 Nm^-2
V₂ =?
T₁ = 273 + 27 = 300 K

∴ According to Boyle’s Law
P₁V₁ = P₂V₂
or
V₂ = \(\frac{P_{1} V_{1}}{P_{2}}=\frac{100 \times 4}{150}\) × 10^-3
= 2.667 × 10^-3 m³
= 2.667 litre.

∴ Change in volume = V₁ – V₂
= 4 – 2.667 = 1.333 litre.

(b) It is then heated at a constant volume so that temperature becomes 127°C. Calculate the new pressure.
Answer:
T₁ = 300 K
T₂ = 273 + 127 = 400 K
P₁ = 150 Nm^-2
P₂ = ?

At constant volume, according to Gay Lussac’s law

Question 7.
The temperature of a gas is – 68°C. To what temperature should it be heated so that
(a) the average K.E. of the molecules be doubled.
(b) the root mean square velocity of the molecules to be doubled?
Answer:
(a) Let θ°C be the temperature of gas up to which it is heated.
∴ T₂ = 273 + θ.
and T₁ = 273 + (- 68)
Let E₂ and E₁ be the average K.E. of the molecules at T₂ and T₁ respectively.

According to the given condition
\(\frac{\mathrm{E}_{2}}{\mathrm{E}_{1}}\) = 2

Using the relation,

(b) Let t°C be the temperature up to which the gas is heated.
∴ T₃ = 273 + t
and T₄ = 273 – 68 = 205 K

Let C₁ and C₂ be the respective r.m.s. velocities of the molecules.
∴ \(\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}\) = 2 (given)

Now using the relation

Question 8.
A balloon contains 500 m³ of He at 27°C and I atm pressure. Find the volume of the helium at 3°C and 0.5 atm pressure?
Answer:
Here, P₁ = 1 atm
T₁ = 27°C = 273 + 27 = 300 K
V₁ = 500 m3
P₂ = 0.5 atm
V₂ = ?
T₂ = – 3°C = 273 – 3 = 270

Using ideal gas equation,
PV = RT, we get
P₁V₁ = RT₁ …(i)
and P₂V₂ = RT₂ …(ii)

Dividing (i) by (ii), we get

Question 9.
At what temperature will the average velocity of O₂ molecules be sufficient so as to escape from earth? V_e = 11.0 km s^-1 and mass of one molecule of O₂ is 5.34 × 10^-26 kg, k = 1.38 × 10^-23 JK^-1.
Answer:
Here, escape velocity from earth surface,
V_e = 11.0 kms^-1
= 11 × 10^-3 ms^-1
k = 1.38 × 10^-23 JK^-1

Mass of one O₂ molecule, M = 5.34 × 10^-26 kg
T = ?
We know that K.E. per molecule is given by

Question 10.
The volume of the air bubble increases 15 times when it rises from the bottom to the top of a lake. Calculate the depth of the lake if the density of lake water is 1.02 × 10³ kg m^-3 and atmospheric pressure is 75 cm of Hg.
Answer:
Here, P₁ = 75 cm of Hg
= 0.75 × 13.6 × 10³ × 9.8 Nm^-2
= 99.96 × 10³ Nm^-2

Let V₂ = volume of bubble at depth h = x
i.e. V₁ = x + 15x = 16x
P₂ = 0.75 m of Hg = hρ_water g
= 99.96 × 10³ + h × 10³ × 9.8

Using Byole’s law,
P₁V₁ = P₂V₂, we get
99.96 × 10³ × 16x = (99.96 × 10³ + h × 10³ × 9.8)x
or
h = \(\frac{15 \times 99.96 \times 10^{3}}{9.8 \times 10^{3}}\) = 153 m.

Question 11.
Two glass bulbs of volumes 500 cm³ and 100 cm³ are connected by a narrow tube of negligible volume. When the apparatus is sealed off, the pressure of the air inside is 70 cm of Hg and temperature 20°C. What does the pressure become if a 100 cm³ bulb is kept at 20°C and the other bulb is heated to 100°C?
Answer:
Here, V₂ = 500 cm³
V₁ = 100 cm³
P₁ = P₂ = P = ?
T₁ = 20°C = 293 K
T₂ = 100°C = 373 K
T = 20°C = 293 K
P’ = 70 cm of Hg

For a given mass of the gas,

Question 12.
0.014 kg of nitrogen is enclosed in a vessel at a temperature of 27°C. How much heat has to be transferred to the gas to double the r.m.s. the velocity of its molecules?
Answer:
V_rms = \(\sqrt{\frac{3 R T}{M}}\)
Here, T₁ = 273 + 27 = 300 K .

Now to double the r.m.s. velocity, the temperature should be raised to four times the initial temperature.
i.e. T₂ = 4T, = 4 × 300 K = 1200 K
∴ ΔT = rise in temperature = T₂ – T₁
= 1200 – 300 – 900 K

k = 1.38 × 10-23 Jk^-1
C_v = \(\frac{5}{2}\) R = \(\frac{5}{2}\)(kN)
= \(\frac{5}{2}\) × 1.38 × 10^-23 × 6.023 × 10²³
= 20.8 JK^-1 mol^-1 …(i)

∴ If Δθ be the amount of heat required,
Then Δθ = n Cv ΔT
where n = number of moles of nitrogen in 0.014 kg
= \(\frac{1}{0.028}\) × 0.014
= \(\frac{1}{2}\) (∵ 1 mole of N₂ = 0.028 Kg)

∴ Δθ = \(\frac{1}{2}\) × 20.8 × 900
= 9360 J.

Question 13.
Four molecules of a gas have speeds 4,6,8 and 10 Km s^-1 respectively. Calculate their rms speed.
Answer:
Here, C₁ = 4 km s^-1
C₂ = 6 km s^-1
C₃ = 8 km s^-1
C₄ = 10 km s^-1
C = rms speed = ?

Question 14.
At what temperature, pressure remaining constant, will the RMS velocity of gas on behalf of its value at 0°C?
Answer:
Here, T₁ = 0°C 273 + 0 = 273 K
Let C₁ = rmsvelocityat0°C
Let T₂ be the temperature (= ?) at which rms velocity becomes half
i.e. C₂ = \(\frac{\mathrm{C}_{\mathrm{I}}}{2}\)

Now using the relation, C₂ ∝ T. we get
\(\frac{C_{2}^{2}}{C_{1}^{2}}=\frac{T_{2}}{T_{1}}\)

Question 15.
If the density of nitrogen at S.T.P. be 0.00125 g cm³. What is the velocity of its molecules? g = 980 cm
Answer:
Here, P = 1 atm = 76 cm of Hg
= 76 × 13.6 × 980 dyne cm^-2
ρ = density of nitrogen
= 125 × 10^-5 g cm^-3
C_rms = ?

Using the relation,

Question 16.
At a certain pressure and 127°C, the average K.E. of a hydrogen molecule is 8 × 10^-27 J. At the same pressure, determine:
(a) ruts velocity of hydrogen molecules at 27°C.
(b) average K.E. of nitrogen molecules at 127°C.
Mass of hydrogen atom = 1.7 × 10^-27 kg.
Answer:
(a) Here, T₁ = 127°C = 127 + 273 = 400 K
E₁ = 8 × 10^-27 J
m = mass of hydrogen molecule
= 2 × 1.7 × 10^-27 kg
= 3.4 × 10^-27 kg

T₂ = 27°C = 27 + 273 = 300 K
E₂ = ?

r.m.s velocity at 27°C, C_rms = ?
Using the relation,
K.E = E ∝ T, we get

Also, we know that

(b) As the average K.E. of a molecule of any gas at the same temperature is the same for all gases, so the average K.E. of nitrogen molecule at 127°C is = 8 × 10^-27 J

Question 17.
Calculate the total random K.E. of one gram of nitrogen at 600 K.
Answer:
Here, T = 600 K
R = 8.31 J/mol/K
M = 28 g = molecular weight of nitrogen

∴ Total random K.E. for 1 g molecule of nitrogen is
E’ = \(\frac{3}{2}\)RT

∴ Total random K.E. for one gram of nitrogen
= \(\frac{3}{2} \frac{\mathrm{R}}{\mathrm{M}}\)T
= \(\frac{3}{2}\) × \(\frac{8.31}{28}\) × 600
= 266.8 J.

Question 18.
Find the temperature at which the RMS velocity of oxygen molecules in the earth’s atmosphere equals the velocity of escape from the earth’s gravitational field.
N = 6.023 × 10²³
R = 6400 km = radius of earth
k = 1.38 × 10^-23 JK^-1
Answer:
Here, N = 6.023 × 10²³
R = 6400 km = 6400 × 10³m
k = 1.38 × 10^-23JK^-1

V_e = escape velocity from earth’s surface
= \(\sqrt{2 \mathrm{gR}_{\mathrm{e}}}\) ….(i)
T = temperature = ?
Let C_rms = rms velocity of oxygen molecules at temp. T0

∴ Using the relation,

Where m = mass of one molecule = \(\frac{M}{N}\)
k = \(\frac{R}{N}\)

∴ According to the statement,

Question 19.
Calculate the temperature at which r.m.s. the velocity of a gas molecule is the same as that of a molecule of another gas at 27°C. The molecular weights of the two gases are 64 and 32 respectively.
Answer:
Here, T₁ = ? :
T₂ = 27°C = 273 + 27 = 300K
M₁ = 64 .
M₂ = 32
C₁ = C₂

∴ Using the relation,

\(\frac{1}{2}\)MC² = \(\frac{3}{2}\)RT,weget
\(\frac{1}{3}\) M₁C₁²= RT₁ for gas of mass M₁
and \(\frac{1}{3}\)M₂C₂² = RT₂ for gas of mass M₂

Question 20.
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 125.0 m³ at a temperature of 127°C and 2 atm pressure, k = 1.38 × 10^-23 JK^-1.
Answer:
Here, T = 127°C + 273 = 400 K
k = 1.38 × 10^-23 JK^-1 P = 2 atmosphere
= 2 × 1.01 × 10⁵ Nm^-2
= 2.02 × 10⁵ Nm^-2

V = volume of room = 125 m³
N’ = no. of molecules in the room =?
∴ R = Nk = 6.023 × 10²³ × 1.38 × 10^-23
= 8.31 JK^-1 mol^-1

Let n = no. of moles of the air in the given volume.
∴ Using gas equation,
PV = nRT, we get
n = \(\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{2.02 \times 10^{5} \times 125}{8.31 \times 400}\)
= 7.60 × 103 moles

∴ N’ = Nn = 6.023 × 10²³ × 7.60 × 10³
= 45.77 × 10²⁶.

Question 21.
Calculate the temperature at which the oxygen molecules will have the same r.m.s. velocity as the hydrogen molecules at 150°C. The molecular weight of oxygen is 32 and that of hydrogen is 2.
Answer:
Here, Molecular weight of oxygen, M0 = 32
Molecular weight of hydrogen. MH = 2

Let T₀ = temp. of oxygen = ?
T_H = temp. of hydrogen
= 150°C = 150 + 273 = 423 K
C₀ = C_H

Question 22.
Calculate the r.m.s. the velocity of molecules of gas for which the specific heat at constant pressure is 6.84 cal per g mol per °C. The velocity of sound in the gas being 1300 ms^-1. R = 8.31 × 10⁷ erg per g mol per °C. J = 4.2 × 10⁷ erg cal^-1.
Answer:
Here, C_p = 6.84 cal/g mol/°C
R = 8.31 × 10 erg/g mol/°C
J = 4.2 × 10 erg/cal
v = velocity = 1300 ms^-1
= 1300 × 100 cm s^-1
C_rms =?

Using the relation,


Now using the relation,

Question 23.
Calculate the molecular K.E. of I g of an oxygen molecule at 127°C. Given R = 8.31 JK^-1 mol^-1. The molecular weight of oxygen = 32.
Answer:
Here, M = 32 g
T = 127 + 273 = 400 K

∴ Molecular K.E. of oxygen is given by
\(\frac{1}{2}\) MC² = \(\frac{3}{2}\) RT
Now K.E. of 32 g of O₂ RT = \(\frac{3}{2}\)RT

∴ K.E.of 1 g of O₂ = \(\frac{3}{2} \cdot \frac{\mathrm{RT}}{32}\)
or
E = \(\frac{3}{64}\) × 8.31 × 400 J
= 155.81 J.

Question 24.
Calculate the intermolecular B.E. in eV of water molecules from the following data:
N = 6 × 10²³ per mole
1 eV= 1.6 × 10^-19 J
L = latent heat of vaporisation of water = 22.6 × 10⁵ J/kg.
Answer:
Here, molecular weight of water, M = 2 + 16 = 18g
∴ No. of molecules in 1 kg of water = \(\frac{6 \times 10^{23}}{18}\) × 1000 = \(\frac{10^{26}}{3}\)

L = 22.6 × 10⁵ J kg
∴ B.E .per molecule = 22.6 × 10⁵ J = B.E of \(\frac{6 \times 10^{23}}{18}\) molecule

Thus B.E. per molecule

Question 25.
Two perfect gases at absolute temperatures T₁ and T₂ are mixed. There is no loss of energy. Find the temperature of mixture if masses of molecules are m₁ and m₂ and the no. of molecules in the gases are n₁ and n₂ respectively.
Answer:
Let E₁ and E₂ be the K.E. of the two gases,
∴ E₁ = \(\frac{3}{2}\) kT₁ × n₁
and E₂ = \(\frac{3}{2}\) kT₂ × n₂

Let E be the total energy of the two gases before mixing
∴ E = E₁ + E₂ = \(\frac{3}{2}\)K(n₁T₁ + n₂T₂) ….(1)

After mixing the gases, let T be the temperature of the mixture of the two gases
∴ E’ = \(\frac{3}{2}\)kT(n₁ + n₂) …(2)

As there is no loss of energy,

Value-Based Type:

Question 1.
Ram has to attend an interview. He was not well. He took the help of his friend Raman. On the way office, Ram felt giddy, He vomited on his dress. Raman washed his shirt. He made Ram drink enough amount of water. In spite of doing, a foul smell was coming from the shirt. Then Raman purchased a scent bottle from the nearby cosmetics shop and applied to Ram. Ram attended the interview, Performed well. Finally, he was selected.
(a) What values do you find in Raman?
Answer:
He has the presence of mind, serves others in need.

(b) The velocity of air is nearly 500m/s. But the smell of scent spreads very slowly, Why?
Answer:
This is because the air molecules can travel only along a zig-zag path due to frequent collisions. Consequently, the displacement per unit time is considerably small.

Question 2.
One day Shikha got up 7a.ni and saw that the rays of sunlight coming through a narrow hole contains some dust particles which is moving randomly. She kept it her mind and when she reached her school the next day, she first asked her physics teacher the reason behind it. The teacher explained that gas consists of rapidly moving atoms or molecules. The particles may also collide with each other when they come together. She becomes happy to hear the reason. ‘
(i) What values are exhibited by Shikha?
Answer:
Creative, Awareness, willing to know the scientific reasons.

(ii) What is r.m.s velocity?
Answer:
The root mean square speed (r.m.s) of gas molecules is defined as the square root of the mean of squares of the speeds of gas molecules.
i.e Vrms = \(\sqrt{\frac{V_{1}^{2}+V_{2}^{2}+V_{3}^{2}+\ldots \ldots \ldots \ldots \ldots .+V_{n}^{2}}{n}}\)
= \(\sqrt{\frac{3 \mathrm{~K}_{\mathrm{B}} \mathrm{T}}{\mathrm{m}}}\)

(iii) Calculate r.m.s velocity of one gram molecule of hydrogen at S.T.P. [density of hydrogen at S.T.P = 0.09 kg m^-3]
Answer:
According to kinetic theory .of gases:
P = \(\frac{1}{3}\)ρC²
or
C = \(\sqrt{\frac{3 \mathrm{P}}{\rho}}\)

Here, ρ = 0.09 kg m^-3, P = 1.01 × 10⁵ Pa.
∴ C = \(\sqrt{\frac{3 \times 1.01 \times 10^{5}}{0.09}}\)
= 1837.5 ms^-1

Question 3.
During the lecture of physics period, Madan’s teacher Mr Suresh has given a question to the whole class. The question was as under:
“A vessel contains two non-reactive gases: neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressure is 3:2.
Estimate the ratio of
(a) Number of molecules
(b) Mass density
Madan raised his hand to answer the above two questions and gave a satisfactory answer to the question. .
(i) What value is displayed by Madan?
Answer:
He is intelligent, Creative, Sharp minded.

(ii) What explanations would have been given by Madan?
Answer:
(a) Since V and T are common to the two gases
Also, P₁V = μ₁ RT ….(i)
P₂V = μ₂ RT….(ii)

[Using ideal gas equation]
Here, 1 and 2 refer to neon and oxygen respectively
i.e \(\frac{P_{1}}{P_{2}}=\frac{\mu_{1}}{\mu_{2}}\)
⇒ \(\frac{3}{2}=\frac{\mu_{1}}{\mu_{2}}\) {∵ \(\frac{P_{1}}{P_{2}}=\frac{3}{2}\)(given)}

(b) By definition μ1 =\(\frac{\mathrm{N}_{1}}{\mathrm{~N}_{\mathrm{A}}}\) and \(\frac{\mathrm{N}_{2}}{\mathrm{~N}_{\mathrm{A}}}\) where N₁ and N₂ are the number of molecules of 1 and 2 and NA is the Avogadro’s number.
∴ \(\frac{N_{1}}{N_{2}}=\frac{\mu_{1}}{\mu_{2}}=\frac{3}{2}\)

Question 4.
A quiz contest was organized by a public school. They asked rapid-fire questions and decided to give l^st, 2nd and 3rd prizes. The entire class was divided into ten groups and each group has S students.
The questions in the final round were as under:
(i) What is the ideal gas equation?
Answer:
The relationship between Pressure P, Volume V and absolute temperature T of a gas is called its equation of state. The equation of the state of an ideal gas is
PV = μRT

(ii) What would be the effect on the RMS velocity of gas molecules if the temperature of the gas is increased by a factor of 4?
Answer:

Clearly, ‘C’ will be doubled.

(iii) Which values are being depicted here by the school by ask¬ing the above questions?
Answer:
Values are:
(a) To develop group activity.
(b) To teach in an interesting way.
(c) Award and prizes to motivate them.
(d) To develop leadership quality.

Here we are providing Class 11 chemistry Important Extra Questions and Answers Chapter 5 States of Matter. Chemistry Class 11 Important Questions are the best resource for students which helps in Class 11 board exams.

Class 11 Chemistry Chapter 5 Important Extra Questions States of Matter

States of Matter Important Extra Questions Very Short Answer Type

Question 1.
What is the pressure of a gas? What is its S.I. unit?
Answer:
The force exerted by the gas molecules per unit area on the walls of the container is equal to its pressure SI. unit of pressure is the pascal (Pa).
1 Pa = Nm^2- =1 kg m^-1s^-2.

Question 2.
What does the temperature of gas represent?
Answer:
The temperature of the gas represents the average kinetic energy of the gas molecules as we know K.E. ∝ \(\sqrt{T}\).

Question 3.
Why is it not possible to cool gas to o K?
Answer:
This is because all gases condense to liquids or solids before this temperature is reached.

Question 4.
What property of molecules of real gases is indicated by van der Waal’s constant ‘a’?
Answer:
Intermolecular attraction.

Question 5.
What do you understand by standard temperature?
Answer:
The standard temperature is 0°C or 273 K.

Question 6.
What is the effect of temperature on the vapour pressure of a liquid?
Answer:
Vapour pressure increases with rising in temperature.

Question 7.
What is an ideal gas equation?
Answer:
For given ideal gas PV = nRT
where P = gas pressure;
V = volume,
R = gas constant
T = Temp. (Kelvin scale);
n – no. of moles of gas.

Combined Gas Law Calculator … Combined gas law is the combination of Charles’s law, Boyle’s law, and Gay-Lussac’s law.

Question 8.
Which state of matter has a definite volume, but no definite shape?
Answer:
Liquid.

Question 9.
What is the value of the gas constant in S.I. units?
Answer:
8.314 JK^-1 mol^-1.

Question 10.
What are the S.I. units of surface tension?
Answer:
Nm^-1

Question 11.
What is the compressibility factor?
Answer:
Z = \(\frac{PV}{nRT}\).

Question 12.
What is the equation of state for real gases?
Answer:
van der Waal’s equation(P + \(\frac{a}{\mathrm{~V}^{2}}\))(v – b) = RT for 1 mole.

Question 13.
How is the pressure of a gas related to its density at a particular temperature?
Answer:
d = \(\frac{MP}{RT}\)

Question 14.
How is the partial pressure of a gas in a mixture related to the total pressure of the gaseous mixture?
Answer:
The partial pressure of a gas = Mole fraction of that gas × total pressure.

Question 15.
What is the relationship between average kinetic energy , and the temperature of a gas?
Answer:
K.E. = \(\frac{3}{2}\)kT
where k is Boltzmann constant = \(\frac{\mathrm{R}}{\mathrm{N}_{0}}\).

Question 16.
What is the significance of van der Waal’s constant ‘a’ and ‘b’?
Answer:
‘a’ is a measure of the magnitude of the intermolecular forces of attraction while ‘b’ is a measure of the effective size of the as molecules.

Question 17.
Arrange the solid, liquid and gas in order of energy-giving reasons.
Answer:
Solids < liquid < gas. This is because a solid absorbs energy to change into a liquid which further absorbs energy to change into a gas.

Question 18.
What is the effect of pressure on the boiling point of a liquid?
Answer:
The boiling point increases as the prevailing pressure increases.

Question 19.
Why are vegetables cooked with difficulty at a hill station?
Answer:
The atmospheric pressure decreases as we go up. Therefore at the hills due to the lowering of atmospheric pressure, boiling points lowered.

Question 20.
The size of the weather balloon keeps on becoming larger as it rises to high altitude. Explain why?
Answer:
At higher altitudes, the external pressure on the balloon decreases and therefore, its size increases.

Question 21.
How is the pressure of a given sample of a gas related to the temperature at a constant volume?
Answer:
P ∝ T, i.e., Pressure varies as absolute temperature.

Question 22.
How is the pressure of a gas related to the number of molecules of a gas at constant volume and temperature?
Answer:
P ∝ N; N = No. of molecules of a gas.

Question 23.
What type of graph do we get when we plot a graph PV against P? What is shown by this graph?
Answer:
It is a straight line parallel to the r-axis. It shows that PV is constant at different pressures. It shows Boyle’s Law.

Question 24.
At what temperature will oxygen molecules have the same kinetic energy as ozone molecules at 30°C?
Answer:
AT 30°C. Kinetic energy depends only on the absolute temperature and not on the identity of the gas.

Question 25.
At a particular temperature why vapours pressure of acetone is less than that of ether?
Answer:
This is because intermolecular forces in acetone are more than those present in ether.

Question 26.
Out of NH₃ and N₂ which will have
(i) a larger value of V and
Answer:
NH₃ will have a large value of ‘a’ because of hydrogen bonding.

(ii) larger value of ‘b’?
Answer:
N2 should have a large value of ‘b’ because of its larger molecular size.

Question 27.
Why are the gases helium and hydrogen not liquefied at room temperature by applying very high pressure?
Answer:
Because their critical temperature is lower than room temperature. Gases cannot be liquefied above the critical temperature by applying even very high pressure.

Question 28.
What will boil at a higher temperature at sea level or at the top of mountains?
Answer:
Water will boil at a higher temperature at sea level.

Question 29.
Under what conditions do real gases tend to show ideal gas behaviour?
Answer:
When the pressure of the gas is very low and the temperature is high.

Question 30.
Both propane (C₃Hg) and carbon dioxide (CO₂) diffuse at the same rate under identical conditions of temperature and pressure. Why?
Answer:
Both propane (C₃Hg) and carbon dioxide (CO₂) have the same molar mass (44 gm).

Question 31.
If the number of moles of a gas is doubled by keeping the temperature and pressure constant, what will happen to the volume?
Answer:
The volume will also double as V ∝ n according to Avogadro’s Law.

Question 32.
What is a Triple point?
Answer:
The temperature at which solid, liquid and vapour; i.e., all the three states of the substance exist together is called the triple point.

Question 33.
Is Dalton’s law of partial pressures valid for a mixture of SO₂ and O₂?
Answer:
No, the law holds good only for those gases which do not react with each other.

Question 34.
Under what conditions a gas deviates from ideal gas behaviour?
Answer:
It deviates at low temperature and high pressure.

Question 35.
Molecule A is twice as heavy as molecule B. Which of these has higher kinetic energy at any temperature?
Answer:
K.E. of a molecule is directly proportional to temperature and is independent of its mass. So both the molecule A and B at any temperature will have equal kinetic energy.

Question 36.
How will you define pascal?
Answer:
It is defined as the pressure exerted by a force of one newton on an area of one meter2.
Pa = 1 Nm^-2.

Question 37.
How will you define London or dispersion forces?
Answer:
The forces of attraction between the induced momentary dipoles are called London or dispersion forces.

Question 38.
What is Absolute Zero?
Answer:
The lowest possible hypothetical temperature of – 273°C at which gas is supposed to have zero volume is called Absolute zero.

Question 39.
What is the nature of the gas constant R?
Answer:

= work done per degree per mole.

Question 40.
What is the value of R in SI units?
Answer:
R = 8.314 JK^-1 mol^-1 = 8.314 k Pa dm³ K^-1 mol^-1

Question 41.
What is meant from Boyle point or Boyle temperature?
Answer:
The temperature at which a real gas behaves like an ideal gas over an appreciable pressure range is called Boyle point or Boyle temperature.

Question 42.
How will you define viscosity?
Answer:
The internal resistance to the flow of a fluid is called its viscosity.

Question 43.
What is the effect of temperature on the viscosity of a liquid?
Answer:
The viscosity of a liquid decreases with an increase in temperature.

Question 44.
How will you convert pressure in atmospheres into SI units?
Answer:
1 atm = 1,01,325 Pa or Nm^-2 or 1 bar = 10⁵ Pa.

Question 45.
What do you understand from surface tension?
Answer:
The surface tension of a liquid is defined as the force acting at right angles to the surface along a one-centimetre length of the. liquid.

Question 46.
What is the effect of the increase in temperature on the surface tension of a liquid?
Answer:
Surface tension decreases in increasing the temperature.

Question 47.
What is the difference between normal boiling point and standard boiling point?
Answer:
When the external pressure is equal to one atmospheric pressure the boiling point is referred to as a normal boiling point, when it is one bar, the boiling point is called its standard boiling point.

Question 48.
What is the difference between vapour and gas?
Answer:
When gas is below its critical temperature, it is called vapour.

Question 49.
What happens if a liquid is heated to the critical temperature of its vapours?
Answer:
The meniscus between the liquid and the vapour disappears, the surface tension of the liquid becomes zero.

Question 50.
Why falling liquid drops are spherical?
Answer:
The surface area of a sphere is minimum. In order to have minimum surface area drops of the liquid become spherical.

States of Matter Important Extra Questions Short Answer Type

Question 1.
Ammonia and Sulphur dioxide gases are prepared in two comers of a laboratory. Which gas will be detected first by a student working in the middle of the laboratory and why?
Answer:
Molecular mass of NH₃ = 17 Molecular mass of SO₂ = 64
NH₃ is a lighter gas and diffuses at a faster speed than SO₂
∴ NH₃ gas will be detected first.
[∵ Acc. to Graham’s law of diffusion \(\frac{r_{1}}{r_{2}}=\sqrt{\frac{d_{2}}{d_{1}}}\)

Question 2.
What is the effect of hydrogen bonding on the viscosity of a liquid?
Answer:
Hydrogen bonding leads to an increase in the effective size of the moving unit in the liquid. Due to an increase in the size and mass of the molecule, there is greater interval resistance of the flow of the liquid. As a result, the viscosity of the liquid rises.

Question 3.
Which are the two faulty assumptions in the kinetic theory of gases.
Answer:

1. There is no force of attraction between the molecules of the gas.
2. The volume of the molecules of the gas is negligibly small as compared to the total space (volume) occupied by the gas.

Question 4.
What is the relationship between the density and molar mass of a gaseous substance? Derive it.
Answer:
Ideal gas equation is PV = nRT
or \(\frac{n}{V}=\frac{p}{R T}\)
Replacing n by \(\frac{m}{M}\), we get

Question 5.
What is meant by the term: Non-ideal or real gas?
Answer:
The gas which does not obey the Cas law:
Boyle’s law, Charles’ law, Avogadro^ law at all temperatures and pressures is a called-non-ideal or real gas. Most of the real gases show ideal behaviour at low pressure and high temperature.

Question 6.
Derive the ideal gas equation PV = nRT.
Answer:
According to Boyle’s law V ∝ \(\frac{1}{P}\) if n and T are constant.
According to Charles’ law V ∝ T at constant P.and n
According to Avogadro’s law V ∝ n at constant T and P
Combining the three laws
In
V ∝ \(\frac{Tn}{P}\)
or
PV ∝ nT
or
PV = nRT where R is a constant of proportionality called universal gas constant.

Question 7.
Why liquids have a definite volume, but no definite shape?
Answer:
It is due to the fact that in liquids intermolecular forces are strong enough to hold the molecules together, but these are strong enough to hold the molecules together, but these forces are not strong enough to fix them into definite or concrete positions as in solids. Hence they possess fluidity but no definite shape.

Question 8.
How do the real gases deviate from ideality above and below the Boyle point?
Answer:
Above their Boyle point, real gases show positive deviations from ideality and the values of Z are greater than one. The forces of attraction between the molecules are very feeble. Below the Boyle point, real gases first show a decrease, in Z value with increasing pressure, the value Of Z increases continuously.

Question 9.
Write down the van der Waals, equation for n moles of a real gas. What do the constants ‘a’ and ‘b’ stand for?
Answer:
(P + \(\frac{a n^{2}}{V^{2}}\)) (V – nb) = nRT
where p, Vindicate gas pressure and its volume. T is the Kelvin temperature of the gas. R is gas constant. Value of ‘a’ is a measure of the magnitude of intermolecular attractive forces within the molecule and is independent of temperature and pressure, ‘rib’ is approximately the total volume occupied by the molecules themselves. ‘a’ and ‘b’ are called van der Waals constants and their value depends upon the nature of the gas.

Question 10.
How is compressibility factor Z related to the real and ideal volume of the gas?
Answer:
Z = \(\frac{P \mathrm{~V}_{\text {real }}}{n \mathrm{RT}}\) …(1)

If the gas shows ideal behaviour, then
Videal = \(\frac{nRT}{P}\) ….(2)

On putting the titis value of nRT in equation (1), we get
Z = \(\frac{\mathrm{V}_{\text {real }}}{\mathrm{V}_{\text {ideal }}}\)

Thus the compressibility factor Z is the ratio of the actual molar volume of a gas to the molar volume of it. if it were an ideal gas at that temperature and pressure.

Question 11.
What do the critical temperature, critical pressure, and critical volume for a gas stand for?
Answer:
The critical temperature is the temperature above which a gas cannot be liquified however large may be the pressure applied on it. The pressure sufficient to liquiíy a gas at its critical temperature is called its critical pressure. The volume of the gas at its crìtical temperature is called its critical volume’.

Question 12.
What do the absolute zero and absolute scale of temperature stand for?
Answer:
The lowest possible hypothetical temperature of – 273°C at which gas is supposed to have zero volume is called Absolute! zero.

Lord Kelvin suggested a new scale of temperature starting with – 273°C and it’s zero. This scale of temperature is called the absolute scale of temperature.

Absolute or Kelvin temperature is given by T, where
T = t°C + 273
t°C stands for the centigrade scale of temperature.

Question 13.
Give one application of Dalton’s law of partial pressures.
Answer:
One application of Dalton’s law of partial pressures is in determining the/pressure of dry gas. Gases are generally collected over water and, so they contain water vapours. The pressure exerted by the water Vapours at-a particular temperature is called the Aqueous Tension. By subtracting the aqueous tension from the ‘ vapour pressure of the moist gas, the pressure of the dry gas can be calculated.
P_{dry gas}= P_{moist gas} – Aqueous Tension (at t°C).

Question 14.
How will you calculate the partial pressure of gas using Dalton’s Law of partial pressures?
Answer:
In a mixture of non-reacting gases A, B, C etc., if each gas is considered to be an ideal gas, then
P_A = n_A \(\frac{RT}{V}\)
P_B = n_B \(\frac{RT}{V}\)
P_C = n_C \(\frac{RT}{V}\)
where n_A, n_B n_C stand for their respective moles in the same vessel .
[V = constant, keeping T constant]
Then according to Dalton’s law ‘

Thus, particle pressure of a. gas – Mole fraction of A × Total pressure.

Question 15.
Is there any effect of the nature of a liquid and temperature on the surface tension of a liquid?
Answer:

1. Effect of nature of the liquid: Surface tension is a property that arises due to the intermolecular forces of attraction among the molecules of the liquid.
2. The surface tension of the liquids generally decreases with an increase in temperature and becomes zero at the critical temperature.

Question 16.
Leaving electrostatic forces that exist between oppositely charged ions, which other intermolecular attractive forces exist between atoms or ions. Mention them.
Answer:

1. van der Waals forces
2. London Forces or Dispersion Forces
3. Dipole-dipole forces
4. Dipole-induced dipole forces
5. Hydrogen bond.

Question 17.
What is the relationship between intermolecular forces and thermal interactions?
Answer:
Intermolecular forces tend to keep the molecules together but the thermal energy of the molecules tends to keep them apart. Three states of matter are the result of a balance between intermolecular forces and the thermal energy of the molecules.
Gas → Liquid → Solid
intermolecular forces increases →
Gas ← Liquid ← Solid
increase in Thermal energy ←

Question 18.
What are the main characteristics associated with gases?
Answer:

1. Gases are highly compressible.
2. Gases exert pressure equally in all directions.
3. Gases have a much lower density than solids or liquids.
4. Gases do not have definite shape and volume.
5. Gases intermix freely and completely in all proportions.

Question 19.
What do you understand by the term? Isotherms and Isobars?
Answer:
Isotherms are the curves plotted by varying pressure against volume keeping temperature constant.

Each line obtained by plotting volume against temperature keeping, pressure constant is called an Isobar.

Question 20.
What are the forces which are responsible for the viscosity of a liquid? Why is glycerol more viscous than water?
Answer:
The forces responsible for the viscosity of the liquids are

• Hydrogen bonding
• van der Waals torches.

Glycerol possesses greater viscosity than water because glycerol has extensive hydrogen bonding in its molecules due to the pressure of three-Oil groups in it as compared to the hydrogen bonding in water molecules.

States of Matter Important Extra Questions Long Answer Type

Question 1.
Derive the Ideal gas equation PV = nRT.
Answer:
Let a certain mass of a gas at pressure P₁ and temperature
T1 occupy a volume V₁. On changing the pressure and temperature respectively to P₂ and T₂, let the volume of the gas change to V₂.
(i) Let us first change the pressure P₁ to P₂ at constant temperature T₁. Then, according to Boyle’s law, volume V is given by,
P₂V = P₁V₁
or
V = \(\frac{P_{1} V_{1}}{P_{2}}\) …(1)

(ii) Now keeping the pressure constant at P₂, heat the gas from temperature T₁ to T₂, the volume changes from V to V₂.
By Charle’s Law, we must have,

The numerical value of k depends upon the amount of gas and the units in which P and V are expressed. By Avogadro’s law, for one mole of any gas, the value of \(\frac{PV}{T}\) will be the same and is represented
\(\frac{PV}{T}\) = R
or
PV = RT.
for n moles of an ideal gas
PV = nRT

Question 2.
State the fundamental assumptions of the kinetic theory of gases
Or
What are the postulates of the kinetic theory of gases?
Or
Write a short note on “Microscopic Model of a gas”.
Answer:
To explain the general properties of gases to provide some theoretical explanation for various gas laws (stated on basis of experimental studies), various, scientists Bernoulli, Clausius, Maxwells, Boltzmann and others, gave ‘Kinetic Theory of Gases’ which explains qualitatively as well as quantitatively the various aspects of gas behaviour.

The important postulates of the theory are:

1. All gases are made up of a very large number of minutes particles called molecules.
2. The molecules are separated from one another by large distances. The empty spaces among the molecules are so large that the actual volume of the molecules is negligible as compared to the total volume of the gas.
3. The molecules are in a state of constant rapid motion in all directions. During their motion, they keep on colliding with one another and. also with the walls of the container and, thus, change their directions.
4. Molecular collisions are perfectly elastic, no loss of energy occurs when the molecules collide with one another or with the walls of the container. However, there may be. redistribution of energy during the collisions.
5. There are no forces of interaction (attractive or repulsive) between molecules. They move completely independent of one another.
6. The pressure exerted by the gas is due to the bombardment of its molecules on the walls of the container per unit area.
7. The average kinetic energy of the gas molecules is directly proportional to the absolute temperature.

Question 3.
Explain the following observations.
(a) Aerated water bottles are kept underwater during summer.
Answer:
Aerated water contains CO₂ gas dissolved in an aqueous solution under pressure and the bottles are well stoppered. As in summer temperature increases and we know that the solubility of the gases decreases with increase in temperature and as a result move of gas is expected to be generated may be large in quantity and hence pressure exerted by the gas may be very high and the bottle may explode. So, to decrease the temperature and hence to avoid explosion of the bottles.

(b) Liquid ammonia bottle is cooled before opening the seal.
Answer:
Liquid ammonia bottle contains the gas under very high pressure. If the bottle is opened as such, then the sudden decrease in pressure will lead to a large increase in the volume of the gas. As a result, the gas will come out of the bottle with force. This will lead to the breakage of the bottle. Cooling under tap water will result in a decrease in volume. It reduces the chances of an accident.

(c) The tyre of an automobile is inflated at lesser pressure in summer than in winter.
Answer:
The pressure of the air is directly proportional to the temperature. During summer due to high temperature, the pressure in the tyre will be high as compared to that in water. The tube may burst under high pressure in summer. Therefore, it is advisable to inflate the tyre to lesser pressure in summer than in winter.

(d) The size of the weather balloon becomes larger and larger as it ascends up to higher altitudes.
Answer:
Answered somewhere else in the book.

States of Matter Important Extra Questions Numerical Problems

Question 1.
In a hospital, an oxygen cylinder holds 10 L of oxygen at 200 atm pressure. If a patient breathes in 0.50 ml of oxygen at 1.0 atm with each breath, for how many breaths the cylinder will be sufficient. Assume that all the data is at 37°C.
Answer:
10 L at 200 atm =? L at 1 atm. [Temp, is constant at 37°C]
∴ Boyle’s law P₁V₁ = P₂V₂ can be applied
200 × 10 = 1 × V₂
or
V₂ = 2000 L

Number of breaths = \(\frac{\text { Total volume }}{\text { Volume inhaled per breath }}\)
= \(\frac{2000 \mathrm{~L}}{0.5 \times 10^{-3} \mathrm{~L}}\)
= 4 × 10⁶

Question 2.
Calculate the pressure of 1 × 10²² molecules of oxygen gas when enclosed ¡n a vessel of 5-litre capacity at a temperature of 27°C.
Answer:
Number f moles of O₂ = \(\frac{1 \times 10^{22}}{6.02 \times 10^{23}}\)

= 0.166 × 10^-1 mol
= 1.66 × 10² mol
The pressure exerted by O₂ molecules can be calculated by the equation
PV = nRT [Ideal gas equation]

Question 3.
When a ship is sailing in the Pacific Ocean where the temperature is 23.4°C, a balloon is filled with 2 L air. What will be the volume of the balloon when the ship reaches the Indian Ocean, where the temperature is 26.1°C.
Answer:
V₁ = 2 L
T₁ = 23.4 + 273 = 296.4K
T₂ = 26.1 + 273 = 299.1 K
From Charle’s Law

Question 4.
At what temperature centigrade, will the volume of a gas at 0°C double itself, pressure remaining constant?
Answer:
Let the volume of the gas at 0°C = V₁ mL
Final Volume = V₂ = 2V₁ mL [Given]
T₁ = OC + 273 = 273 K, T₂ =?

Since Pressure remains constant
∴ Charles law can be applied

Question 5.
A bulb ‘B’ of the unknown volume containing gas at one atmospheric pressure is connected to an evacuated bulb of 0.5-litre capacity through a stop-cock. On opening the stop-cock, the final pressure was found to be 570 mm at the same temperature. ‘What is the volume of bulb ‘B’?
Answer:
Let the volume of the bulb = V₁; P, = 1 atm
Evacuated Bulb has volume = 0.5 L;
Total volume of both bulbs after the opening of stop-cock = (V₁ + 0.5) L i.e. V₂ = (V₁ + 0.5):
P₂ = 570 mm = \(\frac{570}{760}\) atm

Apply Boyle’s law P₁V₁ = P₂V₂
1 × V₁ = \(\frac{570}{760}\) × (V₁ + 0.5)

On solving the above equation
V₁ = 1.5 L
∴ Volume of the unknown bulb ‘B’ = 1.5 L

Question 6.
1 mole of SO2 occupies 1.5 L at 25°C. Calculate the pressure exerted by gas assuming that gas does not obey the ideal gas equation. (Given a = 3.6 atm L²mol^-2, b = 0.04 L mol^-1) where a, b are van der Waal’s constants.
Answer:

Question 7.
A gas occupies a volume of 2.5 L at 9 × 10⁵ Nm^-2. Calculate the additional pressure required to decrease the volume of the gas to 1.5 L, keeping the temperature constant.
Answer:
V₁ = 2.5 L; P₁ = 9 × 10⁵ Nm^-2
V₂ = 1.5 L; P₂ =?

Since temperature is constant, Boyle’s law is applied.

Question 8.
What volume of air will be expelled from a vessel containing 400 cm³ at 7° C when it is heated to 27° C at the same pressure?
Answer:
As the pressure is constant, Charles law is applied

428.6 cm³ is the volume after expansion
∴ Volume expelled = (428.6 – 400) cm³ = 28.6 cm³.

Question 9.
A 10.0 L container is filled with a gas to a pressure of 2.0 atm at 0°C. At what temperature will the pressure of the gas inside the container be 2.50 atm.
Answer:
As the volume of the container remains constant, Gay- Lussac’s Law/Amonton’s Law is applicable
\(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)
\(\frac{2}{273}=\frac{2.50}{\mathrm{~T}_{2}}\)
T₂ = 341 K
or
t₂ = (341 – 273)°C = 68°C.

Question 10.
One litre flask containing vapours of methyl alcohol (Mol. mass = 32) at a pressure of 1 atm and 25°C was evacuated till the final pressure was 10^-3 mm. How many molecules of methyl alcohol were left in the flask?
Answer:
P₁ = 10^-3 mm; V₁ = 1000 cm³; T₁ = 298 K
Converting this volume to volume, at STP, where T₂ = 2/3 K and P₂ = 760 mm

Now, 22400 cm³ at STP contains 6.02 × 10²³ molecules

∴ 1.205 × 10^-3 cm³ at STP contains
= \(\frac{6.02 \times 10^{23}}{22400}\) × 1.205 × 10^-3 molecules
= 3.24 × 10¹⁶ molecules.

Question 11.
A sealed tube that can withstand a pressure of 3 atm is filled with air at 27°C and 760 mm pressure. Find the temperature above which it will burst?
Answer:
Applying gas equation \(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\) as volume of the sealed tube remains constant .
\(\frac{1}{300}=\frac{3}{\mathrm{~T}_{2}}\)
T₂ = 900 K
or
t₂ = 900 – 273 = 627°C.

Question 12.
The temperature at the foot of a mountain is 30°C and pressure is 760 mm. Whereas at the top of the mountain these are 0°C and 710 mm. Compare the densities of the air at the foot and at the top.
Answer:

∴ the ratio of densities of air at the foot and the top of the mountain = 0.964: 1.

Question 13.
10.0 g of O₂ were introduced into an evacuated vessel of 5-litre capacity maintained at 27°C. Calculate the pressure of the gas in the atmosphere in the container.
Answer:
Volume of the gas = V = 5 L;
Wt. of O₂ = 10.0 g
Molar mass of O₂ = 32.0
∴ No. of moles = \(\frac{10}{32}\)

T = 27 + 273 = 300 K; R = 0.0821 L atm K^-1 mol^-1
From ideal gas equation,
PV = nRT, we get
P = \(\frac{10}{32}\) × 0.0821 × 300 = 1.54 atm.

Question 14.
8.0 g of methane is placed in a 5 L container at 27°C. Find Boyle constant.
Answer:
Pressure × Volume is called Boyle’s constant
PV = nRT = \(\frac{W}{M}\) RT ,
= \(\frac{8}{16}\) × 0.0821 × 300
= 12.315 L atm

Question 15.
The density of A gas is 3.80 g L^-1 at STP. Calculate its density at 27°C and 700 torr pressure
Answer:
d = \(\frac{PM}{RT}\)
For the same gas at two different pressures and temperatures,

Question 16.
If the density of a gas at sea level and 0°C is 1.29 kg m^-3, what will be its molar mass (Assume that pressure is equal to 1 bar).
Answer:

Question 17.
A gaseous mixture contains 56 g N₂, 44 g CO₂ and 16 g CH₄ The total pressure of the mixture is 720 mm Hg. What is the partial pressure of CH₄?
Answer:

Question 18.
A 2 L flask contains 1.6 g of methane and 0.5 g of hydrogen at 27°C. Calculate the partial pressure of each gas in the mixture and hence calculate the total pressure.
Answer:
1.6 g CH₄ = \(\frac{1.6}{16}\) = 0.1 Mole
16
Partial pressure of CH4 (pCH4) = CH4 × \(\frac{RT}{P}\)

Question 19.
One mole of S02 gas occupied a volume of 350 mL at 27°C and 50 atm pressure. Calculate the compressibility factor of the gas. Comment on the type of deviation shown by the gas from ideal behaviour.
Answer:
Compressibility factor, Z =
Here n = 1, P = 50 atm, V = 350 × 10^-3 L = 0.35 L
R = 0.0821 L atm K^-1 mol^-1; T = 27 + 273 = 300 K
∴ Z = \(\frac{50 \times 0.35}{1 \times 0.0821 \times 300}\) = 0.711
For an ideal gas Z = 1
As for the given gas Z < 1, it shows a negative deviation, i.e., it is more compressible than expected from ideal behaviour.

Question 20.
A mixture of CO and CO₂ is found to have a density of 1.5 g L^-1 at 20°C and 740 mm pressure. Calculate the composition of the mixture.
Answer:
1. Calculation of average molecular mass of the mixture
M = \(\frac{d R T}{P}=\frac{1.50 \times 0.0821 \times 293}{\frac{740}{760}}\) = 37.06

2. Calculation of percentage composition
Let mol% of CO in the mixture = x
Then mol% of CO? in the mixture = 100 – x

Average molecular mass

Question 21.
A 5-L vessel contains 14 g of nitrogen. When heated to 1800 K, 30% of molecules are dissociated into atoms. Calculate the pressure of the gas at 1800 K.
Answer:
N₂ ⇌ 2N

Initial moles = \(\frac{1.4}{28}\) = 0.05
Moles left = 0.05 – \(\frac{30}{100}\) × 0.05 = 2 × 0.015 = 0.03

∴ Total no. of moles = 0.035 + 0.030 = 0.065
i.e. n = 0.065 mol, V = 5 L, T = 1800 K; P =?
P = \(\frac{n \mathrm{RT}}{\mathrm{V}}=\frac{0.065 \times 0.0821 \times 1800}{5}\)
= 1.92 atm.

Question 22.
Calculate the temperature of 2 moles of S02 gas contained in a 5 L vessel at 10 bar pressure. Given that for SO₂ gas van der Waal’s constant is a – 6.7 bar L² mol^-2 and b = 0.0564 L mol^-1.
Answer:
According to van der Waal’s equation

Question 23.
A given mass of a gas occupies 919.0 mL in a dry state at STP. The same mass when collected over water at 15°C and 750 mm pressure occupies on litre volume. Calculate the vapour pressure of water at 15°C.
Answer:
If p is the vapour pressure of water at 15°C, then P₂ = 750 – p
From the gas equation \(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\), we get
\(\frac{760 \times 919}{273}=\frac{(750-p) \times 1000}{288}\)
or
p = 13.3 mm

∴ Vapour pr. of water = 13.3 mm.

Question 24.
A steel tank containing air at 15 atm pressure at 15°C ¡s provided with a safety valve that will yield at a pressure of 30 atm. To what minimum temperature must the air be heated to below the safety valve?
Answer:
\(\frac{P_{1}}{P_{2}}=\frac{T_{1}}{T_{2}}\)
i.e., \(\frac{15}{30}=\frac{288}{\mathrm{~T}_{2}}\)
or
T₂ = 576 K
or
t₂°C = 576 – 273 = 303°C

Question 25.
Calculate the pressure exerted by 110 g of CO₂ in a vessel of 2 L capacity at 37°C. Given that the van der Waals constants are a = 3.59 L² atm mol^-2 and b = 0.0427 L mol^-1. Compare the value with the calculated value if the gas were considered ideal.
Answer:
According to van der Waals equation

110
Here, n = \(\frac{110}{44}\) = 2.5 moles. Putting the given values, we get
P = \(\frac{2.5 \times 0.0821 \times 310}{(2-2.5 \times 0.0427)}-\frac{3.59 \times 2.5}{2}\)
= 33.61 atm – 5.61 atm = 28.0 atm

If the gas were considered an ideal gas. applying ideal gas equation
PV = nRT
or
P = \(\frac{n \mathrm{RT}}{\mathrm{V}}\)
∴ P = \(\frac{2.5 \times 0.0821 \times 310}{2}\) = 31.8 atm

Here we are providing Class 11 chemistry Important Extra Questions and Answers Chapter 10 The s-Block Elements. Chemistry Class 11 Important Questions are the best resource for students which helps in Class 11 board exams.

Class 11 Chemistry Chapter 10 Important Extra Questions The s-Block Elements

The s-Block Elements Important Extra Questions Very Short Answer Type

Question 1
Which element is found in chlorophyll?
Answer:
Magnesium.

Question 2.
Name the elements (alkali metals) which form superoxide when heated in excess of air.
Answer:
Potassium, rubidium and caesium.

Question 3.
Why is the oxidation state of Na and K always + 1?
Answer:
It is due to their high second ionisation enthalpy and stability of their ions [Na⁺, K⁺].

Question 4.
Name the metal which floats on the water without any apparent reaction with water.
Answer:
Lithium floats on the water without any apparent reaction to it.

Lithium Oxide Formula. Lithium oxide also lithia is an inorganic compound.

Question 5.
Why do group 1 elements have the lowest ionisation enthalpy?
Answer:
Because of the largest size in their respective periods, solitary electron present in the valence shell can be removed by supplying a small amount of energy.

Question 6.
Why does the following reaction
C – Cl + MF → C – F + MCI
proceed better with KF than with NaF?
Answer:
Because larger K+ cation stabilises larger anion.

Question 7.
Amongst Li, Na, K, Rb, Cs, Fr which one has the highest and which one has the lowest ionisation enthalpy?
Answer:
Li has the highest and Fr has the lowest ionisation enthalpy.

Question 8.
What is the general electronic configuration of alkali metals in their outermost shells?
Answer:
ns1 where n = 2 to 7.

Question 9.
What is meant by dead burnt plaster?
Answer:
It is anhydrous calcium sulphate (CaS04).

Question 10.
Name three forms of calcium carbonate.
Answer:
Limestone, chalk, marble.

Question 11.
Which member of the alkaline earth metals family has
(i) least reactivity
Answer:
Be

(ii) lowest density
Answer:
Ca

(iii) highest boiling point
Answer:
Be

(iv) maximum reduction potential?
Answer:
Be.

Question 12.
Why does lithium show anomalous behaviour?
Answer:
Due to its small size and high charge/size ratio.

Question 13.
Out of LiOH, NaOH, KOH which is the strongest base?
Answer:
KOH.

Question 14.
Write the balanced equations for the reaction between
(a) Na₂O₂ and water
Answer:
2Na₂O₂ + 2H₂O → 4NaOH + O₂

(b) KO₂ and water
Answer:
2KO₂ + 2H₂O → 2KOH + H₂O + O₂

(c) Na₂O and CO₂.
Answer:
Na₂O₄^– + CO₂ → Na₂CO₃

Question 15.
Arrange the following in order of increasing covalent character MCI, MBr. MF, MI (where M = alkali metal]
Answer:
MF < MCI < MBr < Ml.
With the increasing size of anion, covalent character increases

Question 16.
Name an element that is invariably bivalent and whose oxide is soluble in excess of NaOH and its dipositive ion has a noble gas core.
Answer:
The element is beryllium (Be) which forms a divalent ion and has a noble gas core [He] 2s²
Be²⁺ = 1 s²
BeO + 2NaOH → Na₂BeO₂ + H₂O

Question 17.
Arrange the following in the increasing order of solubility in water:
MgCl₂, CaCl₂, SrCl₂, BaCl₂.
Answer:
BaCl₂ < SrCl₂ < CaCl₂ < MgCl₂.

Question 18.
State the reason for the high solubility of beryllium chloride in organic solvents.
Answer:
Beryllium chloride is a covalent compound.

Question 19.
Which alkali carbonate decomposes on heating to liberate CO₂?
Answer:
Lithium carbonate [Li₂CO₃]

Question 20.
Why is the solution of an alkali metal in ammonia blue?
Answer:
Due to the presence of ammoniated electrons.

Question 21.
Beryllium oxide has a high melting point. Why?
Answer:
Due to its polymeric nature.

Question 22.
Mention the chief reasons for the resemblance between beryllium and aluminium.
Answer:
Both Be²⁺ and Al³⁺ ions have high polarising power.

Question 23.
State any one reason for alkaline earth metals, in general, having a greater tendency to form complexes than alkali metals.
Answer:
Because of their small size and high charge, alkaline earth metals have a tendency to form complexes.

Question 24.
Amongst alkali metals why is lithium regarded as the most powerful reducing agent in aqueous solution?
Answer:
Lithium is the best reducing agent because it has the lowest reduction potential:
Li⁺ + e^– → Li(s) E_Red = – 3.07V.

Question 25.
Name the metal amongst alkaline earth metals whose salt does not impart any colour to a non-luminous flame.
Answer:
Beryllium does not impart colour to a non-luminous flame.

Question 26.
What is the difference between baking soda and baking powder?
Answer:
Baking soda is sodium bicarbonate (NaHCO₃) while baking powder is a mixture of sodium bicarbonate fNaHC03) and Potassium hydrogen tartrate.

Question 27.
Why does table salt get wet in the rainy season?
Answer:
Table salt contains impurities of CaCl₂ and MgCl which being deliquescent compounds absorb moisture from the air during the rainy season.

Question 28.
Sodium readily forms Na⁺ ion, but never Na²⁺ ion. Explain.
Answer:
After the removal of 1 electron from Na, it has been left with a noble gas core [Ne] which is closer to the nucleus and requires more energy.

Question 29.
Which compound of sodium is used
(i) as a component of baking powder
Answer:
NaHCO₃

(ii) for softening hard water.
Answer:
Na₂CO₃.

Question 30.
Anhydrous calcium sulphate cannot be used as Plaster of Paris. Give reason.
Answer:
Because it does not have the ability to set like plaster of Paris.

Question 31.
Which of the following halides is insoluble in water?
CaF₂, CaCl₂, CaBr₂ and Cal₂.
Answer:
CaF₂.

Question 32.
Predict giving reason the outcome of the reaction.
Lil + KF → …………
Answer:
LiI + KF → LiF + KI
Larger cation stabilises larger anion.

Question 33.
Name three metal ions that play important role in performing several biological functions in the animal body.
Answer:
Na⁺, K⁺, Ca²⁺, Mg²⁺, etc.

Question 34.
Calcium metal is used to remove traces of air from vacuum tubes. Why?
Answer:
Calcium has a great affinity for oxygen and nitrogen.

Question 35.
Why is sodium kept in kerosene oil?
Answer:
To prevent its contact with oxygen and moist air, because sodium reacts with them.

Question 36.
What is brine?
Answer:
An aqueous solution of NaCl in water.

Question 37.
Why caesium can be used in photoelectric cells while lithium cannot be?
Answer:
Cs has the lowest & Li highest ionisation enthalpy. Hence Cs can lose electron very easily while lithium cannot.

Question 38.
In an aqueous solution, the Li⁺ ion has the lowest mobility. Why?
Answer:
Li⁺ ions are highly hydrated in an aqueous solution.

Question 39.
Lithium has the highest ionisation enthalpy in group-1, yet it is the strongest reducing agent. Why?
Answer:
This is because Li has the highest oxidation potential.
Li → Li⁺ + e^–
E°_ox = + 3.07

Question 40.
Name one reagent or one operation to distinguish between
(i) BeSO₄ and BaSO₄
Answer:
BeSO₄ is soluble in water while BaSO₄ is not.

(ii) Be(OH)₂ and Ba(OH)₂
Answer:
Be(OH)₂ dissolves in alkali, while Ba(OH)₂ does not.

Question 41.
Which alkaline earth metal hydroxide is amphoteric?
Answer:
Be(OH)₂.

Question 42.
Which alkali metal is radioactive?
Answer:
Francium (Fr).

Question 43.
Which alkaline earth metal is radioactive?
Answer:
Radium (Ra).

Question 44.
Name the alkali metal which shows a diagonal relationship with Mg.
Answer:
Lithium (Li).

Question 45.
Give the chemical formula of carnallite.
Answer:
KCl.MgCl₂.6H₂O.

Question 46.
Arrange CaSO₄, SrSO₄ & BaSO₄ in order of decreasing solubility.
Answer:
The order of decreasing solubility of these sulphates is CaSO₄, SrSO₄ & BaSO₄.

Question 47.
Why is K more reactive than Na?
Answer:
Since the valence electron of K is relatively at a greater distance than Na & it requires lesser energy to remove it.

Question 48.
Why does Beryllium show similarities with Al?
Answer:
Because of their similarity in charge/radius ratio (Be²⁺ = 0.064 & Al³⁺ = 0.660)

Question 49.
What is magnesia?
Answer:
Magnesium oxide (MgO).

Question 50.
How is Potassium extracted?
Answer:
By electrolysis of a fused solution of KOH.

The s-Block Elements Important Extra Questions Short Answer Type

Question 1.
Why the solubility of alkaline metal hydroxides increases down the group?
Answer:
If the anion and the cation are of comparable size, the cationic radius ‘vill influence the lattice energy. Since lattice energy decreases much more than the hydration energy with increasing ionic size, solubility will increases as we go down the group. This is the case of alkaline earth metal hydroxides.

Question 2.
Why the solubility of alkaline earth metal carbonates and sulphates decreases down the group?
Answer:
If the anion is large compared to the cation, the lattice; energy will remain almost constant within a particular group. Since the hydration energies decrease down the group, solubility will decrease as found for alkaline earth metal carbonates and sulphates.

Question 3.
Why cannot potassium carbonate be prepared by the SOLVAY process?
Answer:
Potassium carbonate cannot be prepared by the SOLVAY process because potassium bicarbonate (KHCO₃) is highly soluble in water, unlike NaHCO₃ which was separated as crystals. Due to its high solubility KHCO₃ cannot be precipitated by the addition of ammonium bicarbonate to a saturated solution of KCl.

Question 4.
What are the main uses of calcium and magnesium?
Answer:
Main uses of calcium:

1. Calcium is used in the extraction of metals from oxides which are difficult to reduce with carbon.
2. Calcium, due to its affinity for O₂ and N₂ at elevated temperatures, has often been used to remove air from vacuum tubes.

Main uses of Magnesium:

1. Magnesium forms alloys with Al, Zn, Mn and Sn. Mg-Al alloys being light in mass are used in aircraft construction.
2. Magnesium (powder and ribbon) is used in flashbulbs, powders incendiary bombs and signals.
3. A suspension of Mg(OH)₂ in water is used as an antacid in medicine.
4. Magnesium carbonate is an ingredient of toothpaste.

Question 5.
What is meant by the diagonal relationship in the periodic table? What is it due to?
Answer:
It has been observed that some elements of the second period show similarities with the elements of the third period situated diagonally to each other, though belonging to different groups. This is called a diagonal relationship.

The cause of the diagonal relationship is due to the similarities in properties such as electronegativity, ionisation energy, size etc. between the diagonal elements. For example on moving from left to right across a period, the electronegativity increases, which on moving down a group, electronegativity decreases. Therefore on moving diagonally, two opposing tendencies almost cancel out and the electronegativity values remain almost the same as we move diagonally.

Question 6.
Why is the density of potassium less than that of sodium?
Answer:
Generally, in a group density increases with the atomic number, but potassium is an exception. It is due to the reason that the atomic volume of K is nearly twice Na, but its mass (39) is not exactly double of Na (23). Thus the density of potassium is less than that of sodium.

Question 7.
The hydroxides and carbonates of sodium and potassium are easily soluble in water while the corresponding salts of magnesium and calcium are sparingly soluble in water. Explain.
Answer:
Sodium and potassium ions (Na⁺ and K⁺) are larger than the corresponding Mg²⁺ and Ca²⁺ ions. Due to this lattice energy of Mg(OH)₂, Ca(OH)₂, MgCO₃ and CaCO₃. (Lattice energy is defined as the energy required to convert one mole of the ionic lattice into gaseous ions.

Thus lattices with smaller ions have higher lattice energies). The hydration energies of Mg²⁺ and Ca²⁺ are higher than Na⁺ and K⁺ because of their smaller sizes. But the difference in lattice energies is much more. Therefore, the hydroxides and carbonates of Mg²⁺ and Ca²⁺ are insoluble in water because of their higher lattice energies.

Question 8.
Why is it that the s-block elements never occur in free state/nature? What are their usual modes of occurrence and how are they generally prepared?
Answer:
The elements belonging to the s-block in the periodic table (i.e. alkali and alkaline earth metals) are highly reactive because of their low ionisation energy. They are highly electropositive forming positive ions. So they are never found in a free state.

They are widely distributed in nature in the combined state. They occur in the earth’s crust in the form of oxides, chlorides, silicates and carbonates.

Generally, a group I metals are prepared by the electrolysis of fused solution.
For example:

1.
At cathode: Na⁺ + e^– → Na
At anode: Cl^– → Cl + e^–
Cl + Cl → Cl₂

2. KOH ⇌ K⁺ + OH^–
At cathode: K+ + e^– → K
At anode: 4OH → 4OH + 4e
4OH → 2H₂O + O₂
or
4OH^– → 2H₂O + O₂ + 4e^–
These metals are highly reactive and therefore cannot be extracted by the usual methods, because they are strong reducing agents.

Question 9.
Explain what happens when
(i) Sodium hydrogen carbonate is heated.
Answer:

(ii) Sodium with mercury reacts with water.
Answer:
2Na-Hg + 2H₂O → 2NaOH + H₂ ↑ + 2Hg

(iii) Fused sodium metal reacts with ammonia.
Answer:

Question 10.
What is the effect of heat on the following compounds?
(a) Calcium carbonate
Answer:

(b) Magnesium chloride hexahydrate
Answer:

(c) Gypsum
Answer:

(d) Magnesium sulphate heptahydrate.
Answer:

Question 11.
Why is it that the s-block elements never occur in a free state? What are their usual modes of occurrence?
Answer:
The elements belonging to s-block in the periodic table. These metals (Alkali & alkaline earth metals) are highly reactive because of their low ionization energy. They are highly electropositive forming positive ions. So they are never found in a free state. They are widely distributed in nature in a combined state. They occur in the earth’s crust in the form of oxides, chlorides, silicates & carbonates.

Question 12.
Explain what happens when:
(a) Sodium hydrogen carbonate is heated.
Answer:
Sodium hydrogen carbonate on heating decomposes to sodium carbonate.

(b) Sodium with Mercury reacts with water.
Answer:
When sodium with mercury reacts with water. It produces sodium hydroxide.

Question 13.
What is the effect of heat on the following compounds:
(a) Calcium carbonate
Answer:

(b) Magnesium chloride hexahydrate
Answer:

(c) Gypsum
Answer:

Question 14.
State as to why
(a) An aqueous solution of sodium carbonate gives an alkaline test.
Answer:
Sodium carbonate gets hydrolise by water to form an alkaline solution.
CO₃^2- + H₂O → HCO₃^– + OH
Due to this, it gives an alkaline test.

(b) Sodium is prepared by electrolytic method & not by chemical method.
Answer:
Sodium is a very strong reducing agent. Therefore, it cannot be isolated by a general reduction of its oxides or other compounds. The metal formed by electrolysis will immediately react with water forming hydroxides. So, sodium is prepared by the electrolytic method only.

(c) Lithium on being heated in the air mainly forms mono-oxide & not the peroxides.
Answer:
Lithium is the least reactive but the strongest reducing agent of all the alkali metals. It combines with air, it forms mono-oxide only because it does not react with excess air.

Question 15.
Like Lithium in group-I, beryllium shows anomalous behaviour in group II. Write three such properties of beryllium which makes it anomalous in the group.
Answer:
1. Beryllium has an exceptionally small atomic size, due to high ionization energy & small atomic size it forms compounds that are largely covalent & its salts are hydrolysed easily.

2. Beryllium does not exhibit coordination N. more than four as in its valence shell (n = 2). There are only four orbitals. The remaining member of the group has co-ordination no. six by making use of group have co-ordination no. six by making use of some d-orbitals.

3. The oxides & hydroxides of beryllium quite unlike the other elements, in this group are amphoteric in nature.

Question 16.
Explain which one Na or K has a larger atomic radius?
Answer:
Potassium has a larger atomic size than sodium because, in K, the outermost electron is in the fourth energy state (4s¹) while in Na, the outer-most electron is in the third energy state (3s¹). That is r (K) > r (Na) since the fourth energy state (n = 4) in K is farther away from the nucleus than the third energy state (n = 3) in Na.

Question 17.
The alkali metals (group-1 elements) form only unipositive cations (M⁺) & not bivalent cations (M⁺²), Give reason.

Answer:
Alkali metals have an ns¹ valence shell configuration. They can give up this electron to form univalent cations & attain stable electronic configuration like their nearest inner gas. Now the removal of an electron from the closed-shell configuration requires a very large amount of energy. Which is not available in chemical reactions. Therefore, the alkali metals form a univalent cation (M⁺) & No divalent cations (M²⁺) are formed.

Question 18.
Complete the following equations:
(a) Ca + H₂O →?
Answer:

(b) Ca(OH)₂ + Cl₂ →?
Answer:
2Ca(OH)₂ + l → Ca(OCl)₂ + CaCl₂ + H₂O

(c) BeO + NaOH →?
Answer:
BeO + 2NaOH → Na₂BeO₂ + H₂O

Question 19.
How calcium carbonate can be changed into
(a) Calcium sulphate
(b) Calcium oxide?
Write a balanced chemical equation in each case.
Answer:
(a) When calcium carbonate is heated with dil. sulphuric acid, calcium sulphate is obtained.
CaCO₃(s) + H₂SO₄(aq) → CaSO₄(s) + CO₂(g) + H₂O(l)

(b) Calcium carbonate is heated at a high temperature between 1070 – 1270 K. It decomposes to give calcium oxide & carbon dioxide.

Question 20.
Explain the following phenomenon by means of balanced equations:
(a) When exhaling is made through a tube passing into a solution of lime water, the solution becomes turbid.
Answer:
Ca(OH)₂ (l) + CO₂ (g) → CaCO₃ (s) + H₂O (l)

(b) The turbidity of solution in (a) eventually disappears when continued exhaling is made through it.
Answer:
CaCO₃(s) + H₂O(l) + CO₂(g) → Ca(HCO₃)₂(aq)

(c) When the solution obtained in (B) is heated turbidity re-appears.
Answer:
Ca(HCO₃)₂(aq) → CaCO₃(s) + H₂O(l) + CO₂(g)

Question 21.
Describe the reactivity of alkaline earth metals with water.
Answer:
The reactivity of alkaline earth metals with water increases with increasing atomic numbers.

1. Beryllium does not react readily even with boiling water.
2. Magnesium reacts very slowly with cold water. While it reacts with hot water at an appreciable rate & liberates hydrogen gas.
   
3. Calcium, strontium & Barium react vigorously even with cold water & form hydroxides & liberate hydrogen gas
   M(s) + H₂O(l) → M(OH)₂ + H₂(g)
   [M = Ca, Sr, Ba]

Question 22.
Compare the reactivity of alkali metals with water.
Answer:
All the alkali metals displace hydrogen from water i.e.
2M + 2H₂O → 2MOH + H₂

Lithium reacts slowly with water, sodium reacts violently & Cs reacts so vigorously that the reaction if not controlled can lead to an explosion.
2Li(s) + 2H₂O(aq) → 2LiOH (aq) + H₂(g) Slow
2Na(s) + 2H₂O(aq) → 2NaOH (aq) + H₂(g) Fast
2Cs(s) + 2H₂O(aq) → 2CsOH (aq) + H₂(g) Violent

Question 23.
Alkaline earth metals are harder than alkali metals. Give reason.
Answer:
Alkaline earth metals are harder than alkali metals because:

1. The atomic radius of alkaline metals is small, atomic mass is high & density is larger than those of alkali metals. Alkaline earth metals have closed packed crystal structure.
2. In alkaline earth metals, the metallic bonding in its crystal is very strong as compared to the crystal of an alkali metal. Therefore, the atoms in the crystal of alkaline earth metals are strongly bonded.

Question 24.
Differentiate amongst Quick lime, Lime water & Slaked lime.
Answer:

Question 25.
The mobilities of alkali metal ions in aqueous solution follow the order
Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺ Give reasons.
Answer:
Smaller ions are expected to have more mobility. But smaller ions such as Li⁺, Na⁺ due to their higher charge density tend to undergo hydration. Hydration increases the mass & effective size of the smaller ion & as a result, the mobility of ions show the trend given.

Question 26.
How is sodium peroxide manufactured? What happens when it reacts with chromium (III) hydroxide? Give it’s two uses.
Answer:
Sodium peroxide is manufactured by heating sodium metal on aluminium trays in the air (free-from CO₂).
2Na + O₂ (air) → Na₂O₂

Sodium Peroxide oxidises chromium (III) hydroxide to sodium chromate.

Uses:

• It is used as a bleaching agent because of its oxidising, power.
• It is used in the manufacture of dyes & many other chemicals such as benzoyl peroxide, sodium perborate etc.

Question 27.
List three properties of Lithium in which it differs from the rest of the alkali metals.
Answer:
(a) Lithium is much harder, its melting & boiling points are higher than the other alkali metals.
(b) Lithium is the least reactive but the strongest reducing agent among all the alkali metals.
(c) LiCl is deliquescent & crystallise as a hydrate, LiCl.2H₂O whereas other alkali metal chlorides do not form hydrates.

Question 28.
Why is LiF almost insoluble in water whereas LiCl is soluble not only in water but also in acetone?
Answer:
The low solubility of LiF is due to its high lattice enthalpy. LiCl has much higher solubility in water. This is due to the small size of Li⁺ ion & much higher hydration energy.

Question 29.
What happens when
(1) Calcium nitrate is heated,
Answer:

(2) Chlorine reacts with slaked lime
Answer:

(3) Quick lime is heated with silica.
Answer:

Question 30.
Arrange the following in order of property mentioned:
(1) Mg(OH)₂, Sr(OH)₂, Ba(OH)₂, Ca(OH)₂
(Increasing ionic solubility in water)
Answer:
Mg(OH)₂, Ca(OH)₂, Sr(OH)₂, Ba(OH)₂

(2) BeO, MgO, BaO, CaO
(Increasing basic character)
Answer:
BeO, MgO, CaO, BaO

(3) BaCl₂, MgCl₂, BeCl,, CaCl₂
(Increasing ionic character)
Answer:
BeCl₂, MgCl₂, CaCl₂, BaCl₂

The s-Block Elements Important Extra Questions Long Answer Type

Question 1.
What raw materials are used for making cement? Describe the manufacture of Portland cement. What is its approximate composition?
Answer:
Raw materials: The raw materials required for the manufacture of cement are limestone, stone and clay, limestone in calcium carbonate, CaCO₃ and it provides calcium oxide, CaO. Clay- is a hydrated aluminium silicate, Al₂O₃ 2Si02.2H20 and it provides alumina as well as silica. A small amount of gypsum, CaS04.2H20 is also required. It is added in calculated quantity in order to adjust the rate of setting of cement.

Manufacture: Cement is made by strongly heating a mixture of limestone and clay in a rotatory kiln. Limestone and clay are finely powdered and a little water is added to get a thick paste called slurry. The slurry is led into a rotatory kiln from the top through the hopper.

The hot gases produce a temperature of about 1770-1870 K in the kiln. At this high temperature, the limestone and clay present in the slurry combine to form cement in the form of small pieces called clinker. This clinker is mixed with 2 – 3 % by weight of gypsum (CaSO₄ .2H₂O) to regulate the setting time and is then ground to an exceedingly fine powder.

Manufacture of cement

When mixed with water the cement reacts to form a gelatinous mass which sets to a hard mass when three-dimensional cross-links are formed between
…………..Si — O — Si……… and …….. Si — O — Al…… chains.

Composition of cement:
CaO = 50 – 60%
SiO₂ = 20 – 25%
Al₂O₃ = 5 – 10%
MgO = 2 – 3%
Fe₂O₃ = 1 – 2%
SO₃= 1 – 2%

For a good quality cement, the ratio of silica (SiO₂) and alumina (Al₂O₃) should be between 2.5 to 4.0. Similarly, the ratio of lime (CaO) to the total oxide mixtures consisting of SiO₂, Al₂O₃ and Fe₂O₃ should be roughly 2: 1. If lime is in excess, the cement cracks during setting. On the other hand, if lime is less than required, the cement is weak in strength. Therefore, the proper composition of cement must be maintained to get cement of good quality.

By going through these CBSE Class 11 Maths Notes Chapter 15 Statistics Class 11 Notes, students can recall all the concepts quickly.

Statistics Notes Class 11 Maths Chapter 15

Use this online frequency distribution calculator to calculate from discrete frequency distributions.

Before we discuss about the measure of deviations, we are expected to know how to calculate arithmetic mean \(\bar{x}\) and median.
To find mean of a distribution, we proceeded as :
For ungrouped data : x₁, x₁ …….. x_n.
\(\bar{x}=\frac{x_{1}+x_{2}+\ldots+x_{n}}{n}=\frac{\Sigma x_{i}}{n}\)

For discrete frequency distribution

For Continuous Frequency distribution : Let a be the assumed mean.
∴ d_i = x_i – a, h = class interval
and N = Total frequency = f₁ + f₂ + … f_n
Then \(\bar{x}=a+\left(\frac{\Sigma f_{i} d_{i}}{N}\right) \times h\)
To calculate the median, the process is as follows :
For ungrouped data : Arrange the data in ascending or descending order.

If n is odd, \(\left(\frac{n+1}{2}\right)\) th value = Median
If n is even \(\frac{1}{2}\left[\frac{n}{2} \text { th value }+\left(\frac{n}{2}+1\right)^{\text {th }} \text { value }\right]\) = Median
Same method is adopted in case of discrete frequency distribution.

For continuous frequency distribution:
(i) Find the cumulative frequencies :
(ii) \(\frac{\mathrm{N}}{2}\)th or next of \(\frac{\mathrm{N}}{2}\)th cumulative frequency correspond to median class.
(iii) Cumulative frequency C just before \(\frac{\mathrm{N}}{2}\)th c.f. is denoted by C.
(iv) l = lower limit of median class
h = class interval of median class
f= frequency corresponding to median class
Then, median = M = l + \(\left(\frac{\frac{N}{2}-C}{f}\right)\)x h

Measures of dispersion are required to study the degree of scattemess of observations from the central value. The central value may be mean (or median).

Mean deviation from the mean : If a set of n observations x₁ x₂, … x_n have their mean \(\bar{x}\), then mean deviation from the mean \(\bar{x}=\frac{\sum_{i=1}^{n}\left|x_{i}-\bar{x}\right|}{n}\) , where |x_i – \(\bar{x}\)| is the abosolute value of the deviation of x_i from\(\bar{x}\) .

In case, the distribution is a grouped one, the mean deviation from the mean is given by
M.D \((\bar{x})=\frac{\sum_{i=1}^{k} f_{i}\left|x_{i}-\bar{x}\right|}{\sum_{i=1}^{k} f_{i}}\)
where k is the number of classes.

Mean deviation from the median : If a set of n observations are x₁, x₂, x₃, ………….x_n, then mean deviation from the median = M.D. (Med.)
= \(\frac{\Sigma \mid x_{i}-\text { Median } \mid}{n}\)
In case of grouped data, M.D. (Med.) = \(\frac{\Sigma f_{i} \mid x_{i}-\text { Median } \mid}{\Sigma f_{i}}\)

Variance and Standard Deviation: In case of mean deviation from the mean, we take the absolute values of the deviations from the mean, so that their sum does not become zero. Another way is to find the square of the deviations and then add up. It may be possible that \(\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\) in case of distributions having large number of observations but small deviations may be larger than that in case of a distribution having small number of observations but larger deviations which may not be true. As such, to overcome this difficulty, we take average of the squares of deviations.

Thus, variance = \(\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}{n}\) and standard deviation = σ = \(\sqrt{\text { variance }}=\sqrt{\frac{\Sigma\left(x_{i}-\bar{x}\right)^{2}}{n}} .\)

Short-cut Method to Calculate Variance for discrete frequency distribution :

For continuous frequency distribution : Let a be the assumed mean and h be the class interval.
Now, we calculate the variable, y_i as
y_i = \(\frac{x_{i}-a}{h}\)

Comparison of variability of distribution : To compare the variability of two or more distributions, we calculate the coefficient of variation of each distribution, i.e.,
Coefficient of variance (C.V.)
= \(\frac{\text { Standard Deviation }}{\text { Mean }}\) x 100
= \(\frac{\sigma}{x}\) x 100
Greater is the value of coefficient of variation of a distribution, there is more variability in that distribution.

Ascending and descending order calculator is a key tool for users to generate step-by-step

By going through these CBSE Class 11 Maths Notes Chapter 6 Linear Inequalities Class 11 Notes, students can recall all the concepts quickly.

Complex Numbers and Quadratic Equations Notes Class 11 Maths Chapter 6

Important Definitions: (a) A statement involving variable(s) an a sign of inequality, viz. ,>, <, ≥ or ≤ is called an inequality.
(b) Linear inequality : An inequality involving one or two variables in linear power (in single power) is known as linear inequality.
(c) Quadratic inequality: An inequality involving one or two variables in quadratic powers (i.e., in second degree) is known as quadratic inequality.

Important Rules:

Rule 1: Equal numbers may be added to (or subtracted from) both sides of an inequality without affecting the sigh of inequality.
Rule 2: Both sides of an inequality can be multiplied (or divided) by the same positive number. But, when both sides are multiplied or divided by a negative number, then the sign of inequality is reversed.

Solution of System of Linear Inequalities in One Variable
Procedure adopted :

(a) Find all the values of the variables satisfying each of the given inequalities.
(b) Find the values of the variable, which are common to the given inequalities.
These common values of the variables are the solutions of the given inequalities.

Learn about solving inequality calculator using our free math solver with step-by-step solutions.

Note : Range of the values of the solutions of the given inequalities is known as the solution interval of the given inequality.

Graphical Solution of Linear Inequalities in Two Variables

Important definitions : The region containing all the solutions of an inequality is called the solution region.

Note: If an equation involves sign of equality, then the points on the line are also included in the solution. In other cases, these points are not included in the solution. In this case, the line is drawn dotted or broken.

Procedure to Draw Graph of an Inequality

1. First draw the graph of the equation corresponding to the given inequality. To draw the graph of an equation, find the point on the x-axis (by putting y = 0 in the equation) and on they-axis (by putting x = 0 in the equation). Join these two points.

2. This line will divide the coordinate plane in two half plane regions, viz.,
(a) Half plane region I below the line.
(b) Half plane region II above the line.

3. To identify the half plane represented by the inequality, we take a point (a, b) not lying on the line. If putting the point (a, 6) in the inequality, the inequality is satisfied, then the point is situated in the region represented by the inequality otherwise not.

Note : Generally take (0, 0) as the arbitrary point. Sometimes we take the point (1, 1) also.

Solutions of System of Linear Inequalities in Two Variables

Procedure adopted : (a) Draw the graph of the inequalities following the method learnt as stated above reference to the same coordinate axes.
(b) Shade the relevant solution region of each inequality.
(c) Multishaded region will be the solution region of the given inequalities.

Applications : Here in this section, knowledge of solving inequalities will be utilized in solving problems from different fields such as economics, science, mathematics, psychology, etc.

By going through these CBSE Class 11 Maths Notes Chapter 9 Sequences and Series Class 11 Notes, students can recall all the concepts quickly.

Sequences and Series Notes Class 11 Maths Chapter 9

Sequence : A set of numbers arranged according to some definite rule is called a sequence.

The different numbers which form the sequence are called the terms of the sequence. Terms are denoted by the symbols T₁ T₂, T₃, … etc. the subscript denotes the position of the term. The nth term is also called the general term of the sequence.

Sequence containing finite number of terms is called a finite sequence and a sequence is called infinite, if it is not a finite sequence.

In a sequence, we should not always expect that the terms of a sequence will be necessarily given by an algebraic formula. For example, in a sequence of prime numbers 2, 3, 5, 7, …, there is no known formula for the prime numbers. But in the sequence, we do have a rule or law for writing its numbers in order.

Series : If the numbers forming the sequence are connected by the signs of addition (+), we get a series.
The numbers of the series are known as the terms of the series.

Progression : If the terms of a sequence constantly increase or decrease in a set pattern, it is called a progression.

Arithmetic Progression (A.P.) : A sequence in which the difference of any term from the previous term is constant, is called an arithmetic progression and the constant difference is called the common difference.

Avail Infinite Series Calculator Over here to solve your complex problems too easily.

Notation :
(i) The first term is denoted by a.
(ii) The common difference is denoted by d.
(iii) d = T₂ – T₁ = T₃ – T₂ = T₄ — T₃ = … = T_n — T_n-1

nth term or general term of an A.P.: If a be the first term and d, the common difference of an A.P., then T_n = a + (n – 1 )d.
i.e., nth term = first term + (n – 1) x common difference.

Properties of an A.P.: 1. If a constant is added to each term of an A.P., the resulting sequence is also an A.P.

2. If a constant is subtracted from each term of an A.P., then resulting sequence is also an A.P.

3. If each term of an A.P. is multiplied by a constant, then the resulting sequence is also an A.P.

4. If each term of an A.P. is divided by a non-zero constant, then the resulting sequence is also an A.P.

Sum to n terms of an A.P.
(i) S_n = \(\frac{n}{2}\) (a + 1), where T₁ = a, T_n = 1.

(ii) S_n = \(\frac{n}{2}\) [2a + (n – 1)d], where T₁, = a, c.d. = d.

Limit of sequence calculator is the value of the series is the limit of the particular sequence.

Notes:
1. Formula (i) is used, when the last term is known and formula (ii) is used when the common difference is known.
2. These formulae have four quantities each. If three are known, the fourth can be found out.

Arithmetic Means : When three quantities are in A.P., the middle quantity is said to be Arithmetic Mean (A.M.) between the other two.

Thus, if, a, A, 6 are in A.P., then A is the A.M. between a and b.
∴ A-a = b-A [∵Each-c..d.]
⇒ 2A – a + b
A = \(\frac{a+b}{2}\)
A.M. between two numbers = Half their sum

An important result: Sum of n A.M.’s between two quantities is n times the single A.M. between them.
n Arithmetic means : Let A_1, A₂, A₃, …, A_n be the n A.M.’s between two numbers a and b.
The total number of A.M.’s and numbers a and b = (n + 2)
The last term = b.

b = a + (n + 2- 1 )d i.e., d = \(\frac{b-a}{n+1}\)
∴ We can find the A.M.’s as
A₁ = a + d = a + \(\frac{b-a}{n+1}\) , A₂ = a + 2d = a + \(2\frac{b-a}{n+1}\) ……
A_n = a + nd = a + \(n\frac{b-a}{n+1}\).

Geometric progression (G.P.): A sequence in which the ratio of any term to the proceeding term is the same throughout, is called a Geometric Progression and the constant ratio is called the common ratio of G.P.

Standard form of G.P. : If a is the first term and r is the common ratio, then a, ar, ar2, … is the standard form of G.P.

nth term or general term of G.P.:
T_n = ar^n-1>, where T₁ = a and c.r. = r.
The above formula has four quantities a, r, n and T_n. Out of these four, if any three are given, fourth can be found out.

Sum of n terms of a G.P.: If G.P. is a, ar, ar²,…; ar^n-1, then
(i) For, r = 1,
S_n = a + a + a + … + a (n terms)
= na
(ii) For r ≠ 1,
S_n = \(\frac{a\left(1-r^{n}\right)}{1-r}\), if |r| < 1
and S_n =\(\frac{a\left(r^{n}-1\right)}{1-r}\), if |r| > 1

Geometric Means : When three numbers are in G.P., then, middle one is called the Geometric Mean (G.M.) between the other two.

Thus, if a, G, b are in G.P., then G is the G.M. between a and b. It can also be defined as under :
If any number of numbers are in G.P., then all the terms between the first and last terms are called Geometric Means (G.M.’s) between them.

If a, G, b are in G.P. then
\(\frac{\mathrm{G}}{a}=\frac{b}{\mathrm{G}}\)
[v each = common ratio]
G² = ab ⇒ G = \(\sqrt{a b}\) .

An important result: The product of n G.M.’s between a and b is equal to the nth power of the G.M. between a and b.

n-Geometric Means : Let G₁ G₂, G₃, …, G_n be the n G.M.’s between a and b. Total number of terms = n G.M’s and the numbers a and b = n + 2.
∴ (n + 2)th term = last term = b.
If r is common ratio, b = ar^n+2-1 + 2 – 1 = arⁿ⁺¹
r = \(\left(\frac{b}{a}\right)^{n \frac{1}{n+1}}\)
G₁ = ar = a\(\left(\frac{b}{a}\right)^{\frac{1}{n+1}}\) ,
G₂ = ar² = a\(\left(\frac{b}{a}\right)^{\frac{2}{n+1}}\),……. G_n = arⁿ = a\(\left(\frac{b}{a}\right)^{\frac{n}{n+1}}\)

The Sum of Linear Number Sequence Calculator allowed kids & teachers to calculate the sum of the terms of a sequence between two indices of the series.

Sum of first n natural numbers :
Σn = 1 + 2 + 3 + … + n = \(\frac{n(n+1)}{2}\)

Sum of the squares of the first n natural numbers

Σn² = 1² + 2² + 3² + … + n² = \(\frac{n(n+1)(2 n+1)}{6}\)

Sum of the cubes of the first n natural numbers
Σn³ = 1³ + 2³ + 3³ + … + n³ = \(\left[\frac{n(n+1)}{2}\right]^{2}\)

Clearly, Σn³ = (Σn)²

Sum of it terms of a series whose nth term is an³ + bn² + cn + d :
If T_n = an³ + bn² + cn + d, then S_n = aΣn³ + bΣn² 4 cΣz + dn.

Find the sequence calculator tool makes the calculation faster, and it displays the sequence of the function in a fraction of seconds.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 15 Waves. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 15 Important Extra Questions Waves

Waves Important Extra Questions Very Short Answer Type

Harmonic sequence formula is a sequence of real numbers formed by taking the reciprocals of an arithmetic progression.

Question 1.
In a resonance tube, the second resonance does not occur exactly at three times the length at the first resonance. Why?
Answer:
This is due to the end correction.

Question 2.
What is the nature of ultrasonic waves and what is their frequency?
Answer:
Ultrasonic waves are longitudinal waves in nature and have frequencies greater than 20 k Hz.

Question 3.
Is the principle of superposition wave valid in the case of electromagnetic (e.m.) waves?
Answer:
Yes.

Question 4.
A rod is clamped at one end and it is hit by a hammer at the other end
(a) at a right angle to its length
(b) along the length.
What types of waves are produced in each case?
Answer:
(a) Transverse waves
(b) Longitudinal waves.

Question 5.
Why do not we hear beats if the frequency of ìwo sounds is widely different?
Answer:
The beats can’t be heard as separate due to the persistence of hearing if the difference in frequencies is more than 10 Hz.

Question 6.
What causes the rolling sound of thunder?
Answer:
The multiple reflections of the sound of lighting results in the rolling ’ sound of thunder.

Question 7.
A tuning fork produces resonance in a closed pipe. But the ‘ same tuning fork is unable to, produce resonance in an open organ pipe of equal length. Why?
Answer:
It is because the fundamental frequencies of open and closed organ pipes of the same length are different,

Question 8.
Thick and big curtains are preferred in a big hall. Why?
Answer:
To increase the absorption and decrease the reverberation time and hence making the sound uniform,

Question 9.
Why female voice is sweeter than that of a man?
Answer:
This is because the frequency of a lady’s voice is greater than that of a man’s voice.

Question 10.
The frequency of the fundamental note of a tube closed at one end is 200 Hz. What will be the frequency of the fundamental note of a similar tube of the same length but open at both ends?
Answer:
400 Hz.

Question 11.
A wave transmits energy. Can it transmit momentum?
Answer:
Yes.

Question 12.
By how much the wave velocity increases for 1°C rise of temperature?
Answer:
Wave velocity increases by 0.61 ms for 1°C rise of temperature.

Question 13.
Why the sound heard is more in carbon dioxide than in air?
Answer:
This is because the intensity of sound increases with the increase in the density of the medium.

Question 14.
What is the relation between path difference and phase difference?
Answer:
Phase difference = \(\frac{2π}{λ}\) × path difference.

Question 15.
Is it possible to have interference between the waves produced by two violins? Why?
Answer:
No. This is because the sounds produced will not have a constant, phase difference.

Question 16.
The windowpanes of houses sometimes get cracked due to some explosion at a large distance. Which waves are responsible for this?
Answer:
Shockwaves.

Question 17.
Why the velocity of sound is generally greater in solids than in gases?
Answer:
This is because \(\frac{E}{ρ}\) for solids is much greater than for gases.

Question 18.
An observer places his ear at the end of a long steel pipe. He can hear two sounds when a workman hammers the other end of the pipe. Why?
Answer:
This is because the sound is transmitted both through air and medium.

Question 19.
Why a stationary wave is so named?
Answer:
A stationary wave is so named because there is no net propagation of energy. .

Question 20.
How do we identify our friends from his voice while sitting in a dark room?
Answer:
The quality of sound helps us to identify the sound.

Question 21.
Why bells are made of metal and not of wood?
Answer:
This is because the wood has high damping.

Question 22.
What is the nature of light waves?
Answer:
Electromagnetic waves.

Question 23.
When a vibrating tuning fork is moved speedily towards a wall, beats are heard. Why?
Answer:
This is due to the difference in the frequency of the incident wave and the apparent frequency of the reflected wave.

Question 24.
The weight suspended from a sonometer wire is increased by a factor of 4. Will the frequency of the wire be increased exactly by a factor of 2? Justify your answer.
Answer:
No. There will be a slight increase in the length of the wire. So the frequency shall become slightly less than double.

Question 25.
Are sound waves in air longitudinal or transverse?
Answer:
Longitudinal.

Question 26.
Can you notice the Doppler effect if both the listener and the source of sound are moving with the same velocity in the same
direction? Why?
Answer:
No. This is because there is no relative motion between the source of sound and the listener.

Question 27.
If oil of density higher than that of water is used in place of water in a resonance tube, how does the frequency change?
Answer:
The frequency is governed by the air column and does not depend, upon the nature of the liquid. So frequency would not change.

Question 28.
Which property of the medium enables the transverse waves to pass through it?
Answer:
Modulus of rigidity.

Question 29.
In a thunderstorm why flash of light is seen earlier than the sound of thunder?
Answer:
The speed of light is much higher than the speed of sound waves.

Question 30.
What is the main difference between the brazing of a honeybee and the roaring of a lion?
Answer:
Brazing of honeybee is of high pitch and lion’s roar has high intensity.

Question 31.
If you set your watch by the sound of a distant siren, will it go fast or slow?
Answer:
It will go slow due to the low value of the speed of sound in the air.

Question 32.
What is a dispersive medium?
Answer:
A medium in which the wave velocity depends on the frequency of the wave is called a dispersive medium.

Question 33.
Will sound be louder at node or antinode in a stationary wave?
Answer:
It will be louder at node due to large pressure variation there as
ΔP = – strain × elasticity.

Question 34.
Even if a powerful thermonuclear explosion takes place on a planet, the sound is not heard on Earth. Why?
Answer:
The interplanetary space is devoid of continuous material. In the absence of a material, the medium sound is not heard on the earth.

Question 35.
In older days messages were conveyed to distant villages by beating of big drums. Why?
Answer:
It has a larger area and the intensity of sound (I) is directly proportional to the area of an oscillator (A) i.e. I ∝ A.

Question 36.
Which is the most basic property of the wave?
Answer:
Frequency is the basic property of the wave.

Question 37.
You can make waves in a pond by throwing a stone in it. What is the source of energy of the wave?
Answer:
The kinetic energy of the stone is the source of wave energy.

Question 38.
Why echoes are not heard in a small room?
Answer:
Because the minimum distance between the obstacle reflecting sound waves and the source of sound is less than 17 m in a small room, so echoes are not heard.

Question 39.
Name two properties that are common to all types of mechanical waves?
Answer:

1. They require a material medium for their propagation.
2. The medium itself does not move with the wave.

Question 40.
In sound, beats are heard when two independent sources are sounded together. Is it possible in the case of sources of light?
Answer:
No. This is because the phase difference between two independent sources of light is random.

Question 41.
Mention a condition when Doppler’s effect in sound is not applicable.
Answer:
When the velocity of the source or listener exceeds the velocity of sound.

Question 42.
What will be the velocity of sound in a perfectly rigid rod and why?
Answer:
Infinite because the value of Young’s modulus of elasticity is infinite for a perfectly rigid rod.

Question 43.
Sound is simultaneously produced at one end of two strings of the same length, one of rubber and the other of steel. In which string will the sound reach the other end earlier and why?
Answer:
In the case of steel-string as \(\frac{Y}{d}\) ratio is larger for steel than rubber.

Question 44.
Two persons cannot talk on the moon just as they do on the earth. Why?
Answer:
Due to the absence of air on the moon.

Question 45.
Graphs between the pressure P and the speed v in a gas are shown below. Explain with the reason which one is correct?

Answer:
(c) As the speed of sound (y) is independent of pressure, so y remains constant, hence (e) is correct.

Question 46.
Why the bells of colleges and temples are of large size?
Answer:
The larger the area of the source of sound more is the energy transmitted into the medium. Consequently, the intensity of sound is more and loud sound is heard.

Question 47.
State the limitations of Doppler’s effect.
Answer:
Doppler’s effect is applicable only when there is the relative velocity between the source and the listener and is less than the velocity of sound. The effect is not applicable if the relative velocity is greater than the velocity of sound i.e. if the source or observer moves with supersonic velocity.

Question 48.
Animals and human beings have two ears. What help do they render in listening sound from a distant source?
Answer:
The two ears receive sound in different phases, thus they help in locating the direction of the source of the sound. Turning of head and receiving sound in phase turns the direction.

Question 49.
An observer at a sea-coast observes waves reaching the coast. What type of waves does he observe? Why?
Answer:
Elliptical waves while the waves on the surface of the water are transverse, the waves just below the surface of the water are longitudinal. So the resultant waves are elliptical.

Question 50.
Why the reverberation time is larger for an empty hall than a crowded hall?
Answer:
It is due to the fact that the energy absorption in an empty hall is very small as compared to that of the crowded one.

Waves Important Extra Questions Short Answer Type

Question 1.
Here are the equations of three waves:
(a) y (x, t) = 2 sin (4x – 2t)
(b) y (x, t) = sin (3x – 4t)
(c) y (x, t) = 2 sin (3x – 3t).
Rank the waves according to their (A) wave speed and (B) maximum transverse speed, greatest first.
Answer:
(A) b, c, a.
Standard wave equation is y (x, t) = A sin (ωt – kx)
∴ (a) v_a = \(\frac{\omega}{k}=\frac{2}{4}=\frac{1}{2}\) unit = 0.5 unit.

(b) v_b = \(\frac{\omega}{k}=\frac{4}{3}\)unit = 1.33 unit.

(C) V_c = \(\frac{\omega}{k}=\frac{3}{3}\) = 1 unit.
clearly v_b > v_c > v_a, so order is b, c, a.

(b) Transverse speed (vt) = \(\frac{\mathrm{d} y}{\mathrm{dt}}\)
∴ |(v_t)_a| = 2 × 2 = 4
|(v_t)_b| = 4
|(v_t)_c| = 2 × 3 = 6

∴ clearly (c), (a) and (b) tie.

Question 2.
Which physical quantity is represented by the ratio of the intensity of wave and energy density? Why?
Answer:
Velocity.

Question 3.
When are the tones called harmonics?
Answer:
The tones are called harmonics if the frequencies of the fundamental tone and other overtones produced by a source of sound are in the harmonic series.

Question 4.
What will be the effect on the frequency of the sonometer wire if the load stretching the sonometer wire is immersed in water?
Answer:
Due to the upthrust due to buoyancy experienced by the load, the effective weight will decrease, so tension and hence frequency will decrease as v ∝ \(\sqrt{T}\).

Question 5.
An organ pipe is in resonance with a tuning fork. If the pressure of air in the pipe is increased by a factor of 139, then how should the length be changed for resonance?
Answer:
We know that the velocity of sound is independent of pressure, so there is no change in frequency and hence there is no need to change the length of the pipe.

Question 6.
Sound waves travel through longer distances during the night than during the day. Why?
Answer:
Earth’s atmosphere is warmer as compared to the surface of the earth at night. The temperature increases with altitude and thus the velocity of sound increases. It is a case of reflection from denser to rarer medium.

The sound waves get totally internally reflected.

Question 7.
Water is being continuously poured into a vessel. Can you estimate the height of the water level reached in the vessel simply by listening to the sound produced?
Answer:
Yes, the frequency of the sound produced by an air column is inversely proportional to the length of the air column. As the level of water in the vessel rises, the length of the air column in the vessel decreases, so the frequency of sound increases, and hence shrillness of sound increases.

From the shrillness of sound, we can have a rough estimate of the level of water in the vessel.

Question 8.
A sonometer wire resonates with a tuning fork. If the length of the wire between the bridges is made twice even then it can resonate with the same fork. Why?
Answer:
When the length of the wire is doubled, the fundamental frequency is halved and the wire vibrates in two segments so the sonometer wire will still resonate with the given tuning fork.

Question 9.
Doppler’s effect in sound is asymmetric. Explain.
Answer:
Sound waves require a material medium for their propagation.

The apparent frequency is different whether the source moves towards the stationary observer or an observer moves towards the stationary source. Thus the Doppler’s effect is said to be asymmetric. No such asymmetry occurs in light because apparent frequency remains the same in either the case whether the source or the listener moves.

Hence Doppler’s effect is said to be symmetric in light.

Question 10.
What is redshift?
Answer:
It is due to Doppler’s effect in the case of light waves. It is known that all stars are moving away from each other. So apparent frequency of light from a star as received by an observer on earth is less than the actual frequency. Since wavelength is inversely proportional to the frequency, the apparent wavelength of light from stars is more than the actual wavelength.

In other words, due to the Doppler effect, the wavelength of light shifts towards a longer end i.e. towards red color and so it is called redshift.

Question 11.
A sitar wife and a tabla when sounded together give 4 beats/ sec. What do we conclude from this? As the tabla membrane is tightened, the beat rate increases or decreases, explain.
Answer:
When sitar and tabla are sounded together, they give 4 seats/ sec. From this, we conclude that the frequencies of the two sounds differ by 4. If the frequency of tabla is greater than that of a sitar, then on tightening the tabla membrane, the frequency of tabla will further increase and hence the difference in frequencies will increase.

Thus beat rate will increase. If the frequency of tabla is less than that of sitar, then on tightening the tabla membrane, the frequency of tabla will increase and the difference in frequencies will decrease. So beat rate will decrease.

Question 12.
Explain why frequency is the most fundamental property of a wave.
Answer:
When a wave passes from one medium to another, its velocity and wavelength change but the frequency remains the same. Hence frequency is said to be the most fundamental property of a wave.

Question 13.
Sound is produced by vibratory motion, explain why then a vibrating pendulum does not produce sound?
Answer:
The sound which we can hear has a frequency from 20 Hz to 20,000 Hz.

The frequency of the vibrating pendulum does not lie within the audible range and hence it does not produce sound.

Question 14.
Explain why stringed instruments are provided with hollow boxes.
Answer:
The hollow boxes are set into forced vibrations along with the strings. The loudness is higher if the area of the vibrating body is more. So hollow boxes attached to increase the loudness of sound.

Question 15.
When we start filling an empty bucket with water, the pitch of sound produced goes on changing. Why?
Answer:
An empty bucket behaves as a closed organ pipe. The frequency of fundamental note produced by it is given by
v = \(\frac{v}{4l}\).

As the bucket starts filling, the length (l) of the resonating air column decreases, and hence frequency increases. Since the pitch of a sound depends upon the frequency. So it changes with the change in frequency.

Question 16.
Two loud-speakers have been installed in an open space to listen to a speech. When both are operational, a listener sitting at a .particular- place receives a very faint sound. Why? What will happen if one loud-speaker is kept off?
Answer:
When the distance between two loud-speakers from the position of listener is an odd multiple of \(\frac{λ}{2}\), then due to destructive interference between sound waves from two loud-speakers, a feeble sound is heard by the listener.

When one loud-speaker is kept off, no interference will take place and the listener will hear the full sound of the operating loud-speaker.

Question 17.
Why is the sound produced in the air not heard by a person deep inside the water?
Answer:
The velocity of sound in water is much lesser than the velocity of sound in air. So the sound waves are mostly reflected from the surface of the water. Only little refraction of sound from air to water takes place. Moreover, the refracted sound waves die off after traveling a small distance in the water. Hence no sound waves reach deep inside the water.

Question 18.
The reverberation time is larger for an empty hall than a crowded hall. Explain why?
Answer:
The sound prolongs for a longer time in an empty hall as it does not get absorbed. In the case of a crowded hall, the sound is absorbed by the audience. Hence reverberation time is less in the crowded hall.

Question 19.
If a balloon is filled with C0₂ gas, then how will it behave for sound as a lens? On filling it with hydrogen gas, what will happen?
Answer:
The speed of sound in CO₂ is less than in air (∴ v ∝ \(\frac{1}{\sqrt{\rho}}\)). So the balloon filled with CO₂ gas behaves as a concave lens.

When it is filled with hydrogen, the speed of sound in H2 gas becomes greater than in air. So it will behave as a convex lens.

Question 20.
Why on reflection from the rigid surface, the wave does not change type, and only phase change occurs, while on reflection from a smooth surface, type changes while phase does not change?
Answer:
When a compression strikes the rigid surface, the surface does not move but pushes the compression back as such. On the other hand, the direction of vibration of the particles of the medium is reversed. Thus the type of wave does not change while phase change occurs.

When a compression strikes the smooth surface (i.e. yielding surface), the compression continues to move forward with the surface. But due to refraction, a part of the wave moves backward. Thus type changes while phase does not change.

Question 21.
Explain why transverse elastic waves can’t propagate through a fluid?
Answer:
When a transverse elastic wave travels through a solid, a shearing strain develops which is supported by the elastic solid because of the development of a restoring force. Thus elastic waves can propagate through solids.

But a liquid or a gas (i.e. fluid) can’t support a shearing strain. So there will be no restoring forces when there are transverse displacements and so transverse vibrations are not possible.

Question 22.
Two strings of the same material and length under the same tension may vibrate with different fundamental frequencies. Why?
Answer:
The frequency of vibration of the string is given by

If ρ = density of the material of string.
l, r = its length and radius.
D = diameter = 2r, then

Hence the two strings may vibrate with different frequencies when they have different diameters.

Question 23.
Distinguish between transverse waves and longitudinal waves.
Answer:
Longitudinal waves:

1. Particles of the medium vibrate along the direction of propagation of the wave.
2. They travel in the form of alternate compressions and rare¬factions.
3. They can be formed in any medium i.e. solid, liquid, or gas.
4. When these waves propagate, there are pressure changes in ‘ the medium.
5. They can’t be polarised.

Transverse waves:

1. Particles of the medium vibrate, to the direction of propagation of the wave.
2. They travel in the form of alternate crests and troughs.
3. These can be formed in solids and on the surfaces of liquids only.
4. There are no pressure changes due to the propagation of these waves in the medium.
5. They can be polarised.

Question 24.
Distinguish between progressive waves and stationary waves.
Answer:
Progressive waves:

1. The disturbance travels onward. It is1 handed over from one particle to the next.
2. Energy is transported in the medium along with the propagation of waves.
3. Each particle of the medium executes S.H.M. with the same amplitude.
4. No particle of the medium is permanently at rest.
5. Changes in pressure and density are the same at all points of the medium.

Stationary waves:

1. The disturbance is confined to a particular region and there is no onward motion.
2. No energy is transported in the medium.
3. All the particles of the medium except at nodes execute S.H.M. with different amplitude.
4. The particles of the medium at nodes are at rest.
5. The changes of pressure and density are maximum at nodes and minimum at antinodes.

Question 25.
Distinguish between musical sound and noise.
Answer:
Musical sound:

1. It produces a pleasant effect on the ear.
2. It has a high frequency.
3. There are no sudden changes in the amplitude of the musical sound waves.
4. It is a desirable sound.

Noise:

1. It produces an unpleasant effect on the ear.
2. It has a low frequency.
3. There are sudden changes in the amplitude of noise waves.
4. It is an undesirable sound.

Question 26.
What are the characteristics of wave motion?
Answer:

1. Wave motion is a form of disturbance that travels in a medium due to repeated periodic motion of the particles of the medium.
2. The wave velocity is different from the particle velocity.
3. The vibrating particles of the medium possess both K.E. and P.E.
4. The particle velocity is different at different positions of its vibrations whereas wave velocity is constant throughout a given medium.
5. Waves can undergo reflection, refraction, diffraction, dispersion, and interference.

Question 27.
Show that for 1°C change in temperature, the velocity of sound changes by 0.61 ms-1.
Answer:
We know that v ∝ \(\sqrt{T}\) .
If v_t and v_o be the velocity of sound at T°C and 0°C respectively,

where α = \(\frac{\mathbf{v}_{\mathrm{t}}-\mathbf{v}_{0}}{\mathrm{t}}\) is called temp. coefficient of the velocity of sound.

Putting v_o = 332 ms^-1 at T0 i.e. 0°C, we get
α = \(\frac{332}{546}\) = 0.61 ms^-1 °C^-1

Question 28.
An electric bell is put in an evacuated room (a) near the center (b) close to the glass window, in which case the sound is heard (i) inside the room, (ii) out of the room.
Answer:

1. Sound is not heard in cases (a) and (b) inside the room as the medium is not there for the propagation of sound.
2. In case (a) sound cannot be heard outside for the reason given in (i) above.

In case (b) since the bell is very close to the window, the glass pane picks up its vibrations which are conveyed to the eardrum through the air outside the room. So, the sound can be heard in condition (b).

Question 29.
One of the primitive musical instrument is flute, yet produces good musical sound, how?
Answer:
The flute is an open organ pipe instrument having some holes which determine the wavelength and hence the frequency of sound. produced. By closing one or more holes, the length of the vibrating air column is changed and thus different harmonics are produced. The harmonic rich sound is a good musical sound.

Question 30.
Write basic conditions for the formation of stationary waves.
Answer:
The basic conditions for the formation of stationary waves are listed below:

1. The direct and reflected waves must be traveling along the same line.
2. For stationary wave formation, the superposing waves should either be longitudinal or transverse. A longitudinal and a transverse wave cannot superpose.
3. For the formation of stationary waves, there should not be any relative motion between the medium and oppositely traveling waves.
4. The amplitude and period of the superposing waves should be the same.

Question 31.
What is the difference between interference and stationary waves? In which phenomenon, out of the two, energy is not propagated? Why there is no energy at interference minimum?
Answer:
The superposition of two waves close to each other traveling in the same direction produces interference. The energy gets redistributed. It is minimum or zero at points of destructive interference and maximum at points of constructive interference. It is to be noted that the interference minima may not be points of zero energy unless •, the frequencies and amplitudes of the superposing waves are exactly equal.

The superposition of two similar waves (waves having the same amplitude and period) traveling in opposite direction produce stationary waves The nodes have no vibration of particles but antinodes have a maximum amplitude of vibration.

Question 32.
Write the applications of beats.
Answer:
Beats are used to:

1. Determine an unknown frequency by listening to the best frequency Δv. Then unknown frequency V’ = v ± Δv where v is known and it is close to the unknown frequency. The exact value of v’ is found by loading and filling the tuning fork of unknown frequency from which + or – sign is chosen.
2. Tune musical instruments by sounding them together and reducing beats number to zero.
3. Make a sound rich in musical effect by the deliberate introduction of beats between different musical instruments.
4. To produce very low-frequency pulses which otherwise cannot be produced. The beat frequency is the low-frequency sound.
5. Receive radio program by the superheterodyne method.
6. Detect harmful gases in mines.

Waves Important Extra Questions Long Answer Type

Question 1.
Derive expressions for apparent frequency when
(i) source is moving towards an observer at rest.
(ii) the observer is moving towards the source at rest.
(iii) both source and observer are in motion.
Answer:
Let S and O be the positions of. source and observer respectively.
υ = frequency of sound waves emitted by the source.
v = velocity of sound waves.

Case (i) Source (S) in motion and observer at rest: When S is at rest, it will emit waves in one second and these will occupy a space of length v in one second.
If λ = wavelength of these waves, then
λ = \(\frac{v}{υ}\) …(i)

Let vs = velocity of a source moving towards O at rest and let S reaches to S’ in one second. Thus the sound waves will be crowded in length (v – vs). So if λ’ be the new wavelength,
Then λ’ = \(\frac{v-v_{s}}{v}\)

if υ’ be the apparent frequency, then
υ’ = \(\frac{v}{\lambda^{\prime}}=\frac{v}{v-v_{s}}\)υ

∴ υ’ > v i.e. when S moves towards O, the apparent frequency of sound waves is greater than the actual frequency.

(ii) If the observer moves towards the source at rest:

Let v_o = velocity of an observer moving towards S at rest.
As the observer moves towards S at rest, so the velocity of sound waves w.r.t. the observer is v + v_o.

If υ’ = apparent frequency, then
υ’ = \(\frac{\mathbf{v}+\mathbf{v}_{0}}{\lambda}=\frac{\mathbf{v}+\mathbf{v}_{0}}{\mathbf{v}}\)υ
clearly v’ > υ.

(iii) If both S and O are moving
(a) towards each other: We know that when S moves towards stationary observer,

then υ’ = \(\frac{\mathbf{v}}{\mathbf{v}-\mathbf{v}_{\mathrm{s}}}\)

When O moves towards S, then
υ” = \(\left(\frac{v+v_{0}}{v}\right) v^{\prime}=\left(\frac{v+v_{0}}{v-v_{s}}\right) v\)

(b) If both S and O move in the direction of sound waves:
Then the apparent frequency is given by

υ” = \(\left(\frac{\mathbf{v}-\mathbf{v}_{0}}{\mathbf{v}-\mathbf{v}_{\mathrm{s}}}\right)\)υ

(c) When both S and O are moving away from each other:
When source moves away from O at rest, then apparent frequency is given by
υ’ = \(\frac{v}{v+v_{s}}\)υ

When the observer is also moving away from the source, the frequency v’ will change to v” and is given by

Question 2.
Give the analytical treatment of beats.
Answer:
Consider two simple harmonic progressive waves traveling simultaneously in the same direction and in the same medium. Let

• A be the amplitude of each wave.
• There is no initial phase difference between them.
• Let v₁ and v₂ be their frequencies.

If y₁ and y₂ be displacements of the two waves, then
y₁ = A sin 2π v₁ t and
y₂ = A sin 2π v₂ t

If y be the result and displacement at any instant, then
y = y₁ + y₂
= A (sin 2π v₁ t) + sin (2π v₂ t)

is the amplitude of the resultant displacement and depends upon t. The following cases arise.
(a) If R is maximum, then
cos π (v₁ – v₂) t = max. = ±1 = cos nπ
∴ π (v₁ – v₂) t = nπ
or
t = \(\frac{\mathrm{n}}{v_{1}-v_{2}}\) …(3)
where n = 0, 1, 2, …..

∴ Amplitude becomes maximum at times given by
t = \(0, \frac{1}{v_{1}-v_{2}}, \frac{2}{v_{1}-v_{2}}, \frac{3}{v_{1}-v_{2}}\)…..

∴ Time interval between two consecutive maxima is
= \(\frac{1}{v_{1}-v_{2}}\)

∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ – v₂
∴ no. of beasts formed per sec. = v₁ – v₂.

(b) If R is minimum, then

∴ Time interval between two consecutive minima is = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ – v₂
∴ no. of beasts formed per sec. = v₁ – v₂.
Hence the number of beats formed per second is equal to the difference between the frequencies of two component waves.

Question 3.
What conditions are necessary for the good acoustical properties of the building? How are they met?
Answer:
An acoustically good building is one in which the sound is heard clearly in every nook and corner, some conditions must be fulfilled.

These are:
(a) the building should have proper reverberation time, the reverberation time is given by Sabine’s formula which for a hall is
T = \(\frac{0.166 \mathrm{~V}}{\sum \alpha \mathrm{A}}\)
The reverberation time is adjusted by:

1. changing the volume (V): This can be changed little due to the size of the hall already fixed.
2. changing effective absorbing area: This can be done artificially by putting heavy curtains, paintings, providing open windows, wall coverings, etc.
3. providing sufficiently energetic sound: The sound should be sufficiently loud and intelligible at every point.
4. eliminating echo: Except for the desired one, echoes must be eliminated.
5. properly focussing the sound: The sound has to be properly focussed to avoid the source of silence and also unreliable focussing.
6. avoiding unique reinforcement: No single overtone should uniquely be reinforced then the total quality of the note will be affected.
7. avoiding extra noise: Extra noises including resonance within the building has to be avoided.
8. eliminating smooth curved surfaces: Smooth surfaces reflect sound sharply which may cause several problems.

To achieve these goals following steps need to be taken:
(a) Properly design the building to optimize its acoustic condition.
(b) Decorate selectively the building with paintings, floral designs, perforations.
(c) Use false perforated or cardboard ceilings, and perforated structures at the curved walls.
(d) Use carpets, upholster seats with holes in the bottom.
(e) Use carpets or mats etc. on floors.
(f) Heavy curtains, wall hangings, etc. should be used.
(g) Properly place the mike and loud-speakers in the hall.
(h) Avoid sharp corners in the hall and make the stage back parabolic with mike at its focus.

Numerical Problems:

Question 1.
How far does the sound travel in the air when a tuning fork of frequency 280 Hz makes 15 vibrations? Given the velocity of sound is 336 ms^-1.
Answer:
Velocity of sound, v = 336 ms^-1
frequency, v = 280 Hz

∴ Time of one complete vibration,
T = \(\frac{1}{v}=\frac{1}{280}\) s.
Time to complete 15 vibrations,
t = 15 T
= \(\frac{1}{280}\) × 15

If x be the distance covered in time t, then
x = v × t
= 336 × \(\frac{15}{280}\) = 18 m
x = 18 m.

Question 2.
Audible frequencies have a range of 20 Hz to 20 × 10³ Hz.
Express this range in terms of
(i) period T,
(ii) wavelength λ,
(iii) angular frequency CD.
Given the velocity of sound = 340 ms^-1.
Answer:
V = 340 ms^-1
Using v₁ = 20 Hz
v₂ = 20 × 10³ Hz
(i) T = \(\frac{1}{v}\), we get
T₁ = \(\frac{1}{20}\) = 0.005 s
and T₂ = \(\frac{1}{20}\) × 10³
= 0.00005 s = 5 × 10^-5 s.

(ii) we know that

∴ The wavelength range is 17 m to 0.0 17 m.

(iii) Angular frequency, ω = 2πv
∴ ω₁ = 2πv₁ = 2π × 20= 40π rads^-1
ω₂ = 2πv₂ = 2π × 20 × 10³
= 40π × 103 rad s^-1
∴ angular frequency range is 40π rad s^-1 to 40π × 10³ rad s^-1

Question 3.
A copper wire is held at the two ends by rigid supports. At 30°C, the wire is just taut with negligible tension. Find the speed of transverse waves in the wire at 10°C. α = 1.7 × 10^-5 °C^-1, λ = 1.4 × 10¹¹ Nm^-1 and ρ = 9 × 10³ kg m^-3
Answer:
When the temperature changes from 30°C to 10°C, then the change in length of the wire is
Δl = l ∝ Δt = l × 1.7 × 10^-5 × 20
= 3.4 × l × 10^-4 m

Here, ρ = 9 × 10³ kg m^-3
Y = 1.4 × 10¹¹ Nm^-2
Δt = 30 – 10 = 20°C
α = 1.7 × 10^-5 °C^-1

Now Y = \(\frac{\mathrm{F} / \mathrm{a}}{\mathrm{\Delta}l / \mathrm{l}}\)
or
F = Ya \(\frac{Δl}{l}\)
where a = area of cross section of the wire.

Question 4.
The speed of sound in hydrogen is 1270 ms^-1. What will be the speed in a mixture of oxygen and hydrogen mixed in a volume ratio of 1:4?
Answer:
Let V₁ and V₂ be the volumes of O₂ and H₂ respectively in the mixture.
ρ₁ and ρ₂ be their respective densities.

If m1 and m2 be the mass of oxygen and hydrogen respectively, then
m₁ = V₁ρ₁
and m₂ = V₂ρ₂

If ρ be the density of the mixture, then



Also, let v₁ = velocity of sound in the mixture
and v₂ = velocity of sound in the hydrogen
= 1270 ms^-1.

Question 5.
A tuning fork A of unknown frequency is sounded with a tuning fork B of frequency 288. Four beats are heard in one second. Tuning fork A is then loaded with a little wax and again sounded with fork B. Again 4 beats are heard in one second. What is the frequency of A?
Answer:
Since tuning fork A of known frequency say v gives 4 beats/ sec with B of frequency 288, so frequency of tuning fork A is given by
∴ v = 288 ± 4 = 284 or 292.
On loading A with wax, it again produces 4 beats/s with B of frequency 288.

If the frequency of A is 292, it means on loading A with wax, its frequency falls to 284 which can produce 4 beats/s with a B frequency of 288. So the frequency of A maybe 292.

If the frequency of A is 284, on loading it with wax, its frequency falls below 284 so that when it is sounded with B of frequency 288, it forms more than 4 beats/s which is not consistent with the given condition.

So the frequency of A can’t be 284. Hence the frequency of A = 292.

Question 6.
The first overtone of an open organ pipe beats with the first overtone of a closed organ pipe with a beat frequency of 2.2 Hz. The fundamental frequency of a closed organ pipe is 110 Hz. Find the lengths of the pipes. The velocity of sound in air = 330 ms^-1.
Answer:
Fundamental frequency of closed organ pipe is
v_c = \(\frac{\mathrm{v}}{4 \mathrm{~L}_{\mathrm{c}}}\)
L_c = length of closed pipe v
or
L_c = \(\frac{\mathrm{v}}{4 \mathrm{~v}_{\mathrm{c}}}\)

Here, ν_c = 110 Hz
v = 330 ms^-1

∴ L_c = \(\frac{330}{4 \times 110}\) = 0.75m = 75 cm. 0.4 × 110
Now frequency of first overtone of open pipe is
v₁ = \(\frac{\mathrm{v}}{\mathrm{L}_{0}}\)
where L_o = length of open pipe Frequency of first overtone of closed pipe is

Frequency of first overtone of closed pipe is
ν₂ = \(\frac{3 v}{4 L_{c}}=3\left(\frac{v}{4 L_{c}}\right)\)
= 3ν_c = 3 × 110 = 330 Hz

Question 7.
An open pipe is suddenly closed at one end with the result that the frequency of the 3rd harmonic of the closed pipe is found to be higher by loo Hz than the fundamental frequency of the open pipe. What is the fundamental frequency of open pipe?
Answer:
ν_o = \(\frac{v}{2L}\)
where ν0 = fundamental frequency of open pipe. The frequency of the third harmonic of closed pipe is

Question 8.
A set of 24 tuning forks is so arranged that each gives 4 beats per second with the previous one and the last sounds the octave of the first. Find the frequency of the first and last.
Answer:
As the last is the octave (double) of the first, so the frequencies are ¡n the increasing order.
Let frequency of the first = x
frequencyofthe2nd = x + 4
frequency olthe3rd = x + 2(4)
frequency of the 24th = x + 23 (4)
But this is the octave of the first
∴ frequency of the 24th = 2(x) (given)
∴ x + 23(4) = 2x
or
x = 92
∴ frequency of last tuning fork 2 × 92 = 184 Hz.

Question 9.
A drop of water 2 mm in diameter falling from a height of 50 cm in a bucket generates a sound that can be heard from a 5 m distance. Take all gravitational energy difference equal to sound energy, the transformation being spread in time over 0.2s, deduce the average intensity. Take g = 10 ms².
Answer:
Here, ρ of water = 103 kg m^-3
D = 2mm

∴ radius = r = \(\frac{2}{2}\) = 1 mm = 10^-3 m
h = 50cm = 0.50 m
g = 10 ms^-2
d = 5m
∴ a = area in which sound is heard
=4πd²
I = intensity of sound =?

Now I = \(\frac{\text { energy transference }}{\text { time } \times \text { area }}\)
= \(\frac{\text { P.E. of drop }}{\text { time } \times \text { area }}=\frac{m g h}{t \times a}\) …(1)

Question 10.
A train moves towards a stationary observer with a velocity of \(\frac{1}{30}\)th of the velocity of sound. The whistle of the engine regularly blows after one second. What ¡s the interval between successive sounds of the whistle as heard by the observer?
Answer:
Actual time interval between successive blows of whistle = 1 sec.

∴ Actual frequency of whistle, v = 1 Hz
Let v = velocity of sound
∴ velocity of source, vs = \(\frac{v}{30}\)
∴ apparent frequency of the whistle is
ν’ = \(\frac{v}{v-v_{s}}\) × ν = \(\frac{v}{v-\frac{v}{30}}\) × 1
or
ν’ = \(\frac{30}{29}\) Hz

∴ Apparent time interval between two successive sounds of whistle is
t = \(\frac{1}{v^{\prime}}=\frac{29}{30}\) s.

Question 11.
The splash is heard 4.2,3 s after a stone is dropped into a well which is 78.4 m deep. Find the velocity of sound in the air.
Answer:
Here, Depth of well, h = 78.4 m
v = velocity of sound = ?
t = total time after which splash is heard = 4.23 s.
t₁ = time taken by stone to hit water surface in the well.
t₂ = time the sound takes in reaching top of the well.
∴ t₁ +t₂ = 4.23 s
u = 0, g = 9.8 ms^-2, h = 78.4m, t = t₁

using the relation, s = ut + \(\frac{1}{2}\) at², we get

Question 12.
What is the intensity level in dB of sound whose intensity is 10^-6 watt m^-2. Take zero levels of intensity = 10^-2 watt m^-2.
Answer:
Here,
I = 10-6 w m^-2
I₀ = 10^-12 w m^-2

L =?
L = log10 \(\left(\frac{I}{I_{0}}\right)\) = log10 \(\left(\frac{10^{-6}}{10^{-12}}\right)\)
= log₁₀ 10⁶
= 6 log₁₀ 10 = 6 × 1 = 6B
As 1B = 10 dB
∴ L = 6 × 10 = 60 dB

Question 13.
Two closed organ pipes when sounded together produce 12 beats in 4s at a temperature of 27°C. Find the temperature at which the number of beats produced is 16 during the same period.
Answer:
Let v₁ and v₂ be the frequencies produced by the two organ pipes at 27°C. Let v₂₇ be the velocity of sound at 27°C.
and v_t = velocity of sound at t°C
l₁, l₂ be their lengths respectively.

Question 14.
A police-man on duty detects a drop of 15% in the pitch of the horn of a motor car as it crosses him. If the velocity of sound is 330 ms^-1, calculate the speed of a car.
Answer:
v_s = speed of car = ?
v = velocity of sound = 330 ms^-1
v = frequency of sound emitted by horn
If v’ be the apparent frequency’of sound when car approaches the police man, then
ν’ = \(\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_{\mathrm{s}}}\) × ν …(i)

Also let ν” be the apparent frequency of sound when car recedes away from the police man, then
ν” = \(\frac{\mathrm{v}}{\mathrm{v}+\mathrm{v}_{\mathrm{s}}}\) × ν …(ii)

Question 15.
A wire of length 80 cm has a frequency of 250 Hz. If the length of the wire is increased to 100 cm and tension is reduced to \(\frac{1}{4}\)th of its original value, then calculate the new frequency.
Answer:
l₁ = initial length = 80 cm
ν₁ = 250 Hz

Let T₁ = T be the tension
l₂ = 100 cm
T₂ = \(\frac{1}{4}\)T₁ = \(\frac{T}{4}\).
ν = ?

Using the relation

Question 16.
A tuning fork A of unknown frequency is sounded with a tuning fork B of frequency 512 Hz. 8 beats are heard in 1 second. Tuning fork A is then loaded with a little wax and sounded together with B. Again 8 beats are heard in 1 second. Find the frequency of
Answer:
Let ν = frequency of tuning fork A
No. of beats formed/sec. =8
∴ ν = 512 ± 8 = 520, 504

On loading A with wax, it again produces 8 beats/second with B of frequency 512.
Now if ν_A = 520, then it means its frequency decreases on loading. If v. falls to 504 then it will produce 8 beats/sec. with B.
∴ ν_A = 520

If ν_A is 504, then on loading its frequency falls below 504, so it forms more than 8 beats/sec. when sounded together with B which is not consistent with the given condition.

So the frequency of A cannot be 504.
∴ ν_A = 520 Hz.

Question 17.
Two engines pass each other in opposite directions with a velocity of 60 km ph. One of them is emitting a note of frequency 540 Hz. Calculate the frequencies heard in the other engine before and after they have passed each other. The velocity of sound = 316.67 ms^-1.
Answer:
Here, v_s = v_o = 60 kmph = 60 × \(\frac{5}{18}\) = 16.67 ms^-1
ν = 540 Hz
ν’ = ?
v = velocity of sound = 316.67 ms^-1

Case A: Before passing each other:
v = 316.67 ms^-1
v_s = v_o = 16.67 ms^-1
∴ ν’ = ?

Using the relation

Case B: After passing each other:
v_s = – 16.67 ms^-1
v_o = – 16.67 ms^-1
v = 316.67 ms^-1

Question 18.
The audible frequency range of a human ear is 20 Hz to 20 kHz. Convert this into the corresponding wavelength range. Take the speed of sound in the air to be 340 ms^-1.
Answer:
Here, ν₁ = 20 Hz
ν₂ = 20000 Hz
v = 340 ms^-1
λ₁ = ?
λ₂ = ?

∴ λ₁ = \(\frac{v}{v_{1}}=\frac{340}{20}\) = 17 m
and λ₂ = \(\frac{v}{v_{2}}=\frac{340}{20000}\) = 0.017 m

∴ Corresponding wavelength range is 0.017 to 17 m.

Question 19.
For aluminum, the bulk modulus and the modulus of rigidity are 7.5 × 10¹⁰ Nm^-2 and 2.1 × 10¹⁰ Nm^-2. Find the velocity of longitudinal and transverse waves in the medium. The density of aluminum is 2.7 × 10³ kg m^-3.
Answer:
Here, for aluminium, ρ = 2.7 × 10³ kg m^-3 .
η = 2.1 × 10¹⁰ Nm^-2
k = 7.5 × 10¹⁰ Nm^-2
v_l = velocity of longitudinal waves = ?
v_t = velocity of transverse waves = ?

Using the relation,


Also using the relation, for transverse waves,

Question 20.
The velocity of sound at 27°C is 350 ms^-1. If the density of air at N.T.P. is 1.293 kg m^-3, calculate the ratio of the specific heats of air.
Answer:
Here, T = 27 + 273 = 300k
v₂₇ =. velocity of sound at 27°C
= 350 ms^-1
ρ = 1.293 kg m^-3
T_o = 273 k
v_o = velocity at N.T.P. = ?
P = 76 cm of Hg
= 0.76 × 13600 × 9.8 Nm^-2

Using the relation,

Using the relation,

Question 21.
A tuning fork B produces 6 beats per second with another tuning fork of frequency 288 Hz. The tuning fork of unknown frequency is filed and the number of beats now produced is 4 per second. Calculate the frequency of the tuning fork.
Answer:
Known frequency of the fork =288 Hz
No. of beats/second = 6
∴ Unknown frequency = 288 ± 6 = 294 or 282.

When the prongs of tuning fork B are filed, its frequency increases. If the frequency of B is originally 294 Hz, on filing it will increase. So the difference between the frequencies will increase and hence no. of beats will also increase.

If the frequency of B is originally 282 Hz, then on filing it, its frequency will increase, so the difference between the frequencies will decrease, and hence the no. of beats will decrease.

In this case, when the prongs of B are filed, the no. of beats decreases from 6 to 4. Thus the frequency of the given tuning fork is 282 Hz.

Question 22.
Find the change in the frequency observed by a listener when a source approaching him with a velocity of 54 km h^-1 starts going away from him with the same velocity. Take velocity of sound = 330 ms^-1 and v = 300 Hz.
Answer:
Here, v_s = 54 km h^-1 = 54 × \(\frac{5}{18}\) = 15 ms^-1
v = 330 ms^-1
ν = 300 Hz
Case I: When the source is approaching, then
ν’₁ = \(\frac{\mathbf{v}}{\mathbf{v}-\mathbf{v}_{\mathbf{s}}}\)ν = \(\frac{330}{330-15}\) × 300
= 314 Hz

Case II: When the source reduces then
ν’₂ = \(\frac{\mathbf{v}}{\mathbf{v}+\mathbf{v}_{\mathbf{s}}}\)ν = \(\frac{330}{330+15}\) × 300
= \(\frac{330}{345}\) × 300
= 287 Hz

∴ Change in frequency,
ν’₁ – ν’₂ = 314 – 287 = 27 Hz.

Question 23.
A progressive wave is given by
y = 12 sin (5t – 4x)
On this wave, how far away are the two points having a phase difference of \(\frac{π}{2}\)?
Answer:
Here, ΔΦ = phase difference = \(\frac{π}{2}\)

Let Δx be the corresponding path difference,

Question 24.
The figure here shows the wave, y = A sin (ωt – kx) at any instant traveling in the +x direction. What is the slope of the curve at B?

Answer:
Here, the particle velocity is maximum at B and is given by
v_o = ωA.
Also, wave velocity is given by
C = \(\frac{ω}{k}\)
∴ So the slope \(\frac{v_{0}}{C}=\frac{\omega A}{\omega / k}\) = kA

Question 25.
Two sound waves
y₁ = A₁ sin 1000 π(t – \(\frac{x}{220}\) )
and y₂ = A₂ sin 1010 π(t – \(\frac{x}{220}\) ) are superposed. What is the frequency with which the amplitude varies?
Answer:
Rate of variation of amplitude is equal to the beat frequency.
Here, 2πν₁ = 1000 π
or
ν₁ = 500
and 2πν₂ = 1010 π
or
ν₂ = 505

∴ beat frequency = ν₂ – ν₁
= 505 – 500
= 5.

Value-Based Type:

Question 1.
A group of students went to a place on an excursion. While boating on seawater, the students identified a submerged Torpedo-shaped structure. The boys debated among themselves on what they saw. A student by the name of Sharath considering it as a threat informed the police. The police took necessary steps to protect the country from the enemy submarine. Sharath was rewarded.
(a) What can you say about the qualities exhibited by Sharath?
Answer:
Navigator is a responsible citizen, he is duty-minded, having a presence of mind.

(b) A SONAR system fixed in a submarine operates at a frequency of 40 kHz. An enemy submarine moves towards the
SONAR with a speed of 360 km/hr. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to bel450 m/s.
Answer:
Here, frequency of SONAR (Source) = 40 k Hz
= 4 × 10³ Hz
Speed of the sound wave, V = 1450 m/s
Speed of the observer, V_o = 360 kM/h = 100 m/s

∴ Apparent frequency received by an enemy submarine ;
V’ = \(\left(\frac{V+V_{0}}{V}\right) \cdot V=\left(\frac{1450+100}{1450}\right)\) × 40 × 10³
=4.276 × 10⁴ Hz.

This frequency is reflected by the enemy submarine (Source) and observed by SONAR (Now observer).
In this case, Apparent frequency is given by
V” = \(\left(\frac{V}{V-V_{s}}\right) \times V^{\prime}=\left(\frac{1450}{1450-100}\right)\) × 4.276 × 10⁴
=45.9k Hz

Question 2.
Jagat and Ram are working in the same company. Jagat has noticed that Ram is suffering from Cancer. Ram is not aware of this. When Jagat asks him to go for a checkup, Ram refused. He gets convinced how even when he realizes normal, it is very important to get the checkup done once a year.
(a) What according to you, are the values displayed by Jagat in helping Ram.
Answer:
He has concern for hi^ friend, also he has the knowledge of medical facilities available

(b) A hospital uses an ultrasonic scanner to locate tumors in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km/s? The operating fre¬quency of the scanner is 4.2 MHz.
Answer:

that is λ = 4.05 × 10^-4 m

Question 3.
‘Preeti a student of class XI was reading the newspaper, The Headlines in the Newspaper were about the earthquake that had taken place in Assam on the previous day. She was very depressed seeing the loss of life and property. She approached her physics teacher and got the information about how an earthquake occurs.
(a) What can you say about the inquisitiveness of Preeti?
Answer:
She has concern for society and is sympathetic towards others.

(b) Earthquake generates sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of the S wave is about 4 km/s, and that of the P wave is 8 km/s. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in a straight line, how far away does the earthquake occur?
Answer:
LetV₁ and V₂ be the velocities of S waves and P waves and t₁ , t₂ be the time taken by these waves to travel to the position of seismograph. If l is the distance of occurrence of earthquake from the seismograph, .
∴ l = V₁ t₁ = V₂t₂
⇒ 4t₁ = 8 t₂
or
t₁ = 2 t₂ [∴ V₁ = 4 kmh^-1 ,V₂ = 8 kmh^-1]

Also, t₁ – t₂ = 4 min = 240 S.
2t₂ – t₂ = 240 [Using (i)]
or
t₂ = 240 S and t₁ = 2 × 240 = 480 S.
l = v₁ t₁ = 4 × 480 = 1920 km

Question 4.
Rajesh was waiting for the train on the platform with his parents. They were going to Mumbai and the train arrived half an hour late. He felt that when the train was coining towards the station, the intensity of the sound of the whistle was gradually increasing and on the platform the sound was maximum and when the train passes away the intensity of the whistle was decreasing.
Rajesh got confused and asked his father the reason behind it. His father could not give the correct answer. So, he decided to ask his physics teacher.
(i) What are the values displayed here by Rajesh?
Answer:
Values displayed by Rajesh are:
Awareness, curiosity, creativity, and intelligence,

(ii) Write the answer given by your teacher.
Answer:
The teacher explained that it is due to “Doppler’s effect”. Whenever there is a relative motion between the source and observer O. There is a change in observed frequency. So, the apparent frequencies of sound heard by the listener are different from the actual frequency of the sound of the source, which is given by.
V = V_o\(\left(\frac{V+V_{0}}{V+V_{s}}\right)\)

Here, V is the speed of sound through the j medium, V_o is the velocity of the observer relative to the medium, and Vs is the source velocity relative to the medium.

By going through these CBSE Class 11 Maths Notes Chapter 8 Binomial Theorem Class 11 Notes, students can recall all the concepts quickly.

Binomial Theorem Notes Class 11 Maths Chapter 8

Expanding binomials calculator. This calculators lets you calculate expansion of a binomial in your website.

Binomial theorem for any positive integer
1. (a + b)ⁿ = ⁿC₀aⁿ + ⁿC₁a^n-1 + ⁿC₂a^n-2 + ………………..ⁿC_ra^n-rb^r + ………..+ ⁿC_nbⁿ

2. T_r+1 = general term = ⁿC_ra^n-rb^r … (1)
(a + b)ⁿ = \(\sum_{r=0}^{n}\)ⁿC_ra^n-rb^r

3. Some observations : (i) Number of terms in binomial expansion = Index of the binomial + 1 = n + 1.

(ii) In the successive terms of the expansion, the index of the first term is n and it goes on decreasing by unity. Thus, the indices of first term and n, n – 1, n – 2, …, 1, 0 while the index of second term starts from 0 and goes on increasing by 1. Therefore, the indices of second term are 0, 1, 2, … , n.

(iii) In any term of the expansion, the sum of indices of first term and second term is constant and it is equal to n.

(iv) Coefficients of these terms in the expansion are ⁿC₀, ⁿC₁, ⁿC_r. ……, ⁿC₂….., ⁿC_n

Note : These coefficients may also be denoted as
C (n, 0), C(n, 1), C (n, 2),…, C (n, r), …, C (n,n).

To find their values, we apply the formula

Whenever r > \(\frac{n}{2}\) , apply the formula
ⁿC_r = ⁿC_n-r
These coefficients may also be obtained with the help of Pascal’s triangles.

Now look at this pattern :
(a) First row; index 0; coefficient = 1.
(b) Second row; index 1; coefficients are 1, 1. A triangle is inserted between 1 and 1 as shown above.
(c) Third row; index 2; coefficients are 1, 2, 1.

Method : Two triangles, are drawn below each number of 1 of the second row. Adding 1 and 1 of second row we get 2 which is put below the third vertex of triangle. Write 1 each at the beginning arid end.

(d) Fourth row, index 3; coefficients are 1, 3, 3, 1. Method : Insert three triangles below 1, 2 and 1. 1 + 2 = 3 is written below the third vertex of first triangle, 2 + 1 = 3 is written below the second triangle.

Further, we proceed in the same manner.
(v) Coefficients ⁿC₀, ⁿC₁, ⁿC₂…, ⁿC_r, ⁿC_n in Binomial Theorem are known as Binomial Coefficients.

(vi) Replacing b by – b, in (1), we obtain
(a-b)ⁿ = ⁿC₀aⁿ – ⁿC₁a^n-1b + ⁿC₂a^n-2b² + ……….(-1)ⁿⁿC_ra^n-rb^r + ……….ⁿC_n(-b)ⁿ

(vii) Putting a = 1, b = x in (1), we obtain
(1+x)ⁿ = ⁿC₀ + ⁿC₁x + ⁿC₂x² + ……ⁿC_rx^r + …….. + ⁿC_nxⁿ

(viii) Putting a = 1, b = – x in (1), we obtain
(1-x)ⁿ = ⁿC₀ – ⁿC₁x + ⁿC₂x² – ….+ⁿC_r(-x)^r + …… + ⁿC_n(-x)ⁿ

(ix) Putting a = 1, b = 1 in (1), we obtain
(1+1)ⁿ = 2ⁿ = ⁿC₀ + ⁿC₁ + ⁿC₂ + ………..+ⁿC_n

(x) Putting a = 1, b = – 1, we obtain
0 = ⁿC₀ – ⁿC₁ + ⁿC₂ – ⁿC₃ + …..
or ⁿC₀ + ⁿC₂ + ⁿC₄ + ….. = ⁿC₁ + ⁿC₃ + …………+ ⁿC_r + ………

4. Middle Term : The expansion (a + b)n has n + 1 terms.
(i) If n + 1 is odd, the middle term is th = \(\frac{(n+1)+1}{2}\) th \(\frac{(n+2)}{2}\)th term.
(ii) If n + 1 is even, then
1st middle term = \(\frac{n+1}{2}\)th term
2nd middle term = \(\left(\frac{n+1}{2}+1\right)\)th term

Here we are providing Online Education NCERT Solutions for Class 11 English Hornbill Chapter 6 The Browning Version. Students can get Class 11 English The Browning Version NCERT Solutions, Questions and Answers designed by subject expert teachers.

Online Education The Browning Version NCERT Solutions for Class 11 English Hornbill Chapter 6

The Browning Version NCERT Text Book Questions and Answers

The Browning Version Understanding the text

Question 1.
Comment on the attitude shown by Taplow towards Crocker-Harris.
Answer:
Taplow has very more bitter feelings about his teacher Crocker-Harris. He is a student in the lower fifth grade and feels that he would specialise next term if he got his remove, of which he is uncertain as Mr Crocker-Harris doesn’t tell the students the results like the other teachers. As a rule, the class results should only be announced by the headmaster on the last day of term but Taplow feels that none other than Mr Crocker-Harris waits to inform students of their result. He is not interested in the Classical literature that is taught by Mr Crocker-Harris.

He feels science is more interesting than studying Classics such as The Agamemnon, which he calls “muck”. Moreover, he does not like the way it is taught to them. The Agamemnon had a lot of Greek words and Mr Crocker-Harris punished them for not getting them right.

Taplow feels more bitter as he had been given extra work to do for missing a day of school the previous week when he was ill. It was the last day of school and he wished to play golf instead. It was just on the previous day that Mr Crocker- Harris had told Taplow that he had got what he deserved. Taplow feels that Mr Harris might have given him lesser marks to make him do extra work. He adds that Mr Harris is “hardly human”. He also imitates his teacher.

When Frank suggests that Taplow could go and play golf, Taplow is shocked as nobody takes that kind of liberty with Mr Crocker-Harris. Taplow calls Mr Crocker-Harris, “the Crock”, and says that he is worse than a sadist. If he were a sadist, he wouldn’t be as frightening because he would then show he had some feelings. His inside, feels Taplow, is like a “shrivelled nut” and he seems to hate people who like him.

However, Taplow admits that despite everything Mr Crocker-Harris does, he still likes him. Although, he says that Mr Crocker-Harris feels uncomfortable about people liking him. He says once in class Mr Crocker-Harris made one of his classical jokes, and nobody laughed because nobody understood it. However Taplow knew that it was meant to be funny, so he laughed. Mr Crocker-Harris said that he was pleased with Taplow’s knowledge of Latin and wanted him to explain the joke to the rest of the class.

Question 2.
Does Frank seem to encourage Taplow’s comments on Crocker-Harris?
Answer:
Taplow comes to meet Mr Crocker-Harris when he meets Frank. From his conversation with Taplow, Frank realises that the boy does not like Mr Crocker-Harris. Frank then confirms with Taplow, “You sound a little bitter, Taplow.” He then pretends to console him by reasoning that he would get his remove the next day for taking on extra work. Taplow vents his dislike for Mr Harris and says that he is “hardly human”.

But after saying so, he apologises to Frank for talking too much. Frank pretends to be unhappy but asks Taplow to “repeat” what Mr Harris had said to him. Taplow imitates him. Frank pretends to look strict and asks him to be.quiet. He then asks Taplow at what time he was supposed to meet Mr Crocker-Harris. He then tells Taplow that Mr Crocker-Harris was already ten minutes late and suggests that Taplow could go and play golf.

Taplow is shocked and expresses his apprehension if Mr Crocker-Harris should know. Frank envies the effect Mr Crocker-Harris seems to have on boys in the class; they seem to be scared to death of him. Taplow confesses that Mr Crocker-Harris, unlike any other person, does not care for being liked. Frank attempts to instigate Taplow by deriding students for using the teacher’s need to be liked to their own advantage. Taplow remarks that a few teachers were sadists, and Mr Crocker-Harris was worse because he had no feelings.

When Taplow recounts the episode when he had laughed at Mr Crocker-Harris’s jokes, and Mr Crocker-Harris wanted ‘ him to explain it to the rest of the class, but Frank just laughs at that. He, thus, seems to enjoy the low opinion Taplow has of Mr Crocker-Harris.

Question 3.
What do you gather about Crocker-Harris from the play?
Answer:
Mr Crocker-Harris is an old Classics teacher at a British public school, where he’s been teaching for many years. He apparently wants the children to work hard at their lessons and it is for this reason that he has called Taplow to his office. Unfortunately, students do not like him and neither do they like his teaching methods. Taplow feels science is more interesting than studying Classics such as The Agamemnon, which he calls “muck”.

Moreover, he does not like the way it is taught to them. It has a lot of Greek words and Mr Crocker-Harris punishes them for not getting them right. Taplow feels Mr Harris might have given him lesser marks to make him do extra work. He adds that Mr Harris is “hardly human”. Thus underlining that Mr Harris has lost the student’s trust and respect.

He is a fastidious and a rule-bound person who is the only one who follows the rule of letting the headmaster announce the results on the last day of term.Taplow imitates Mr Crocker-Harris but all the same is frightened of letting Mr Harris know. The students seem to be scared to death of him. Calling Mr Crocker-Harris, the Crock, Taplow says that he is worse than a sadist as he shows no feelings.

He feels uncomfortable about people liking him. Mr Harris does not seem to respond to students who try to warm up to him. When Taplow laughed at his joke, Mr Crocker-Harris had wanted him to explain it to the rest of the class. The poor man is an unfortunate teacher.

The Browning Version Talking about the text

Discuss with your partners

Question 1.
Talking about teachers among friends.
(Answers will vary)

Question 2.
The manner you adopt when you talk about a teacher to other teachers.
(Answers will vary)

Question 3.
Reading plays is more interesting than studying science.
(Answers will vary)

The Browning Version Working with words

Question 1.
A sadist is a person who gets pleasure out of giving pain to others. Given below are some dictionary definitions of certain kinds of persons. Find out the words that fit these descriptions.
Answer:

• A person who considers it very important that things should be correct or genuine, for example, in the use of language or in the arts: Perfectionist/Purist
• A person who believes that war and violence are wrong and will not fight in a war: Pacifist
• A person who believes that nothing really exists: Nihilist
• A person who is always hopeful and expects the best in all things: Optimist
• A person who follows generally accepted norms of behaviour: Conformist
• A person who believes that material possessions are all that matter in life: Materialist