Category: CBSE Class 8

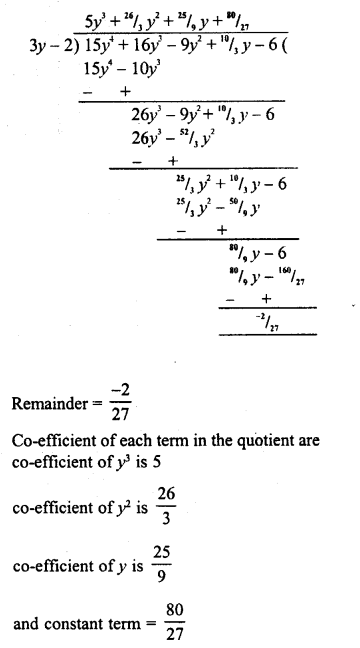
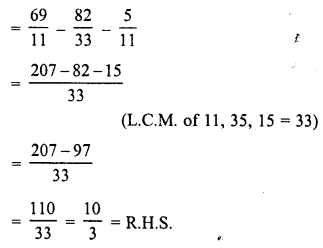
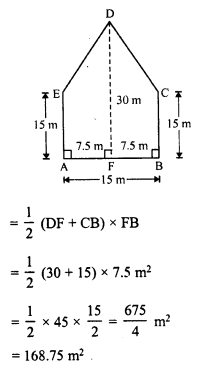
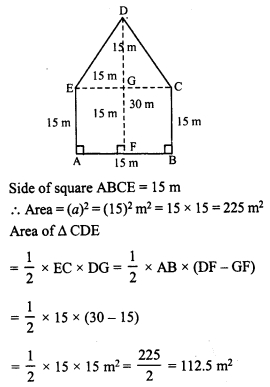
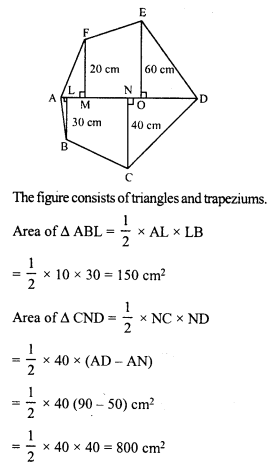
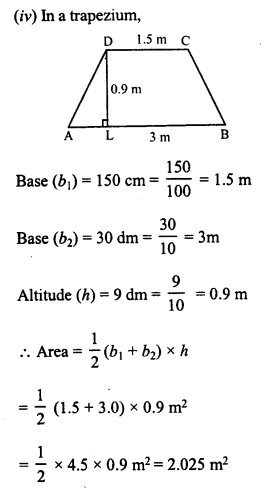
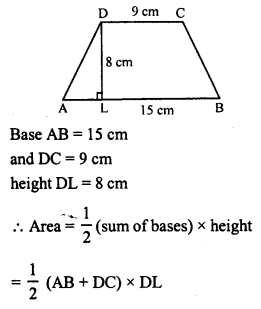
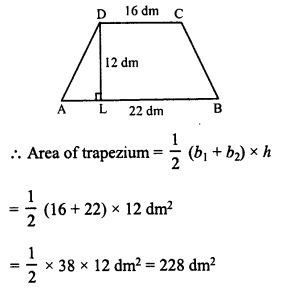
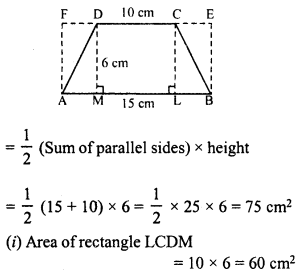
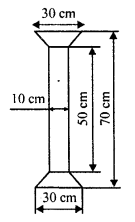
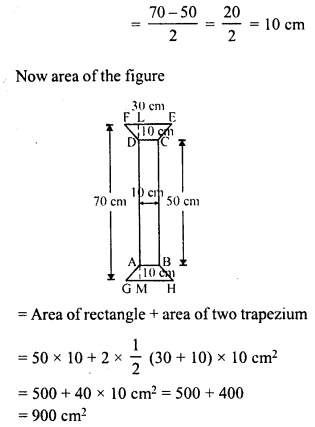
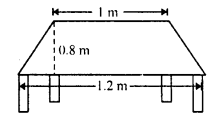
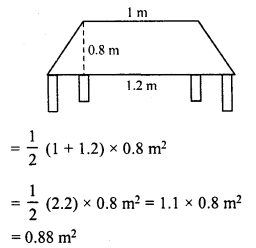
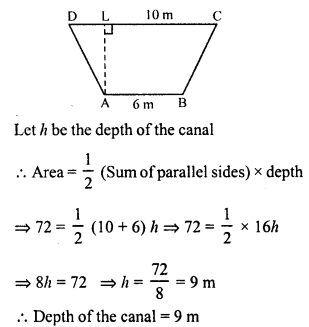
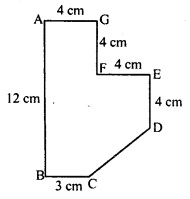
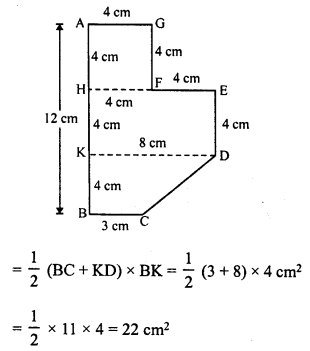
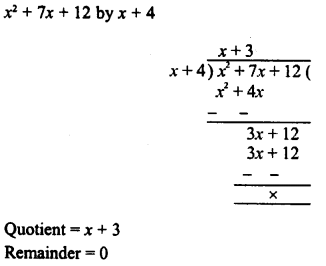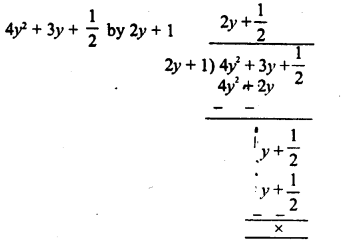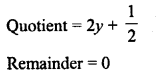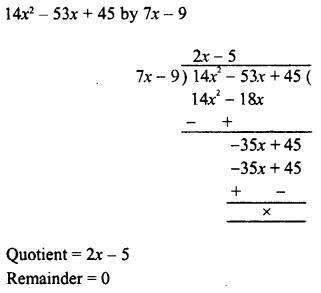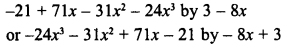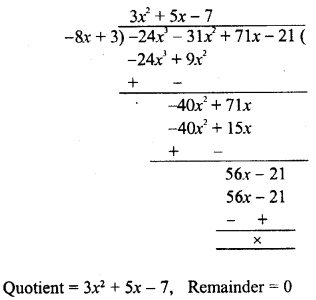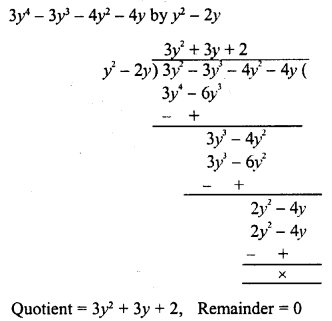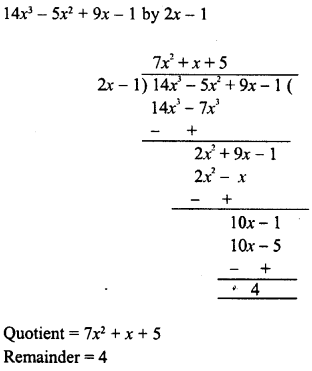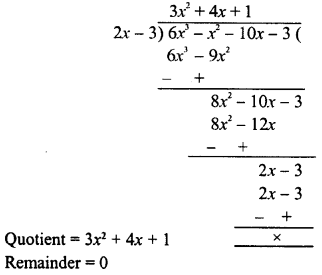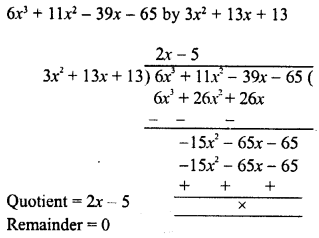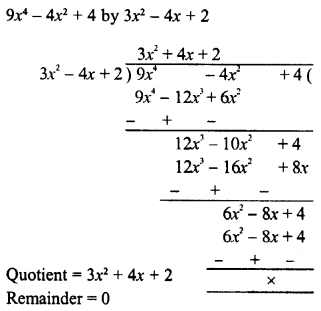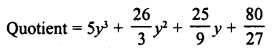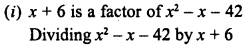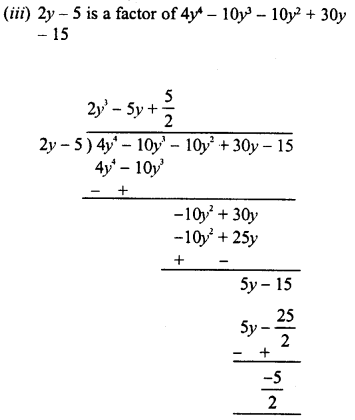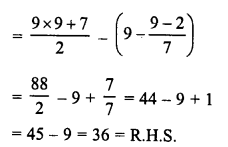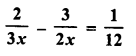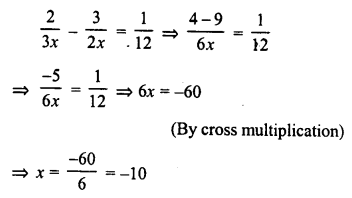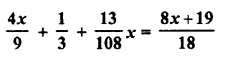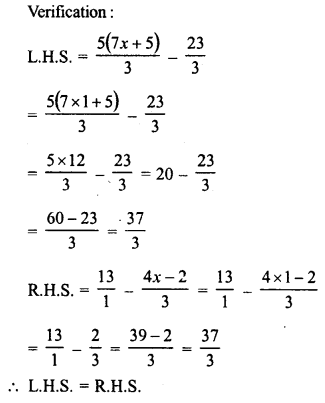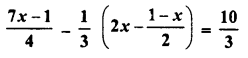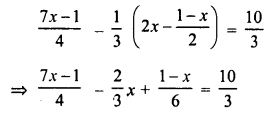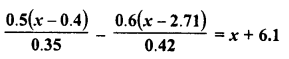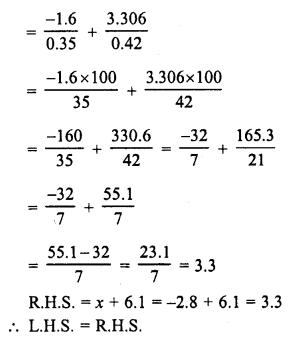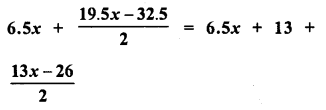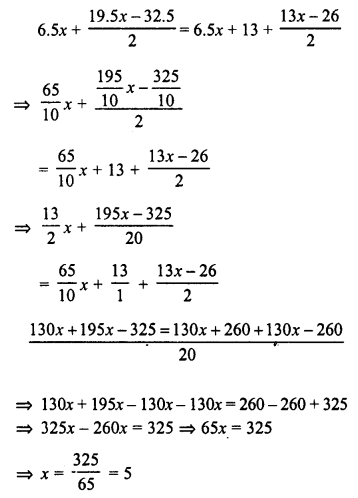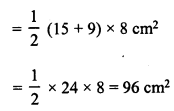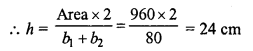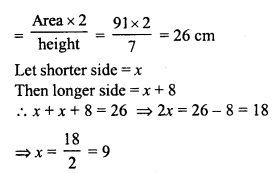RD Sharma Class 8 Solutions Chapter 7 Factorization Ex 7.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.7
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.8
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9

Factorize each of the following algebraic expressions.

Question 1.
6x (2x – y) + 7y (2x – y)
Solution:
6x (2x – y) + 7y (2x – y)
= (2x – y) (6x + 7y)
[∵ (2x – y) is common]

Question 2.
2r (y – x) + s (x – y)
Solution:
2r (y – x) + s (x – y)
-2r (x – y) +s (x – y)
= (x – y) (-2r + s)                   [(x – y) is common]
= (x-y) (s-2r)

Question 3.
7a (2x – 3) + 2b (2x – 3)
Solution:
7a (2x – 3) + 3b (2x – 3)
= (2x – 3) (7a + 3b)               [(2x – 3) is common]

Question 4.
9a (6a – 5b) – 12a² (6a – 5b)
Solution:
9a (6a – 5b) – 12a² (6a – 5b)
HCF of 9 and 12 = 3
∴ 3a (6a – 5b) (3 – 4a)
{(6a – 5b) is common}

Question 5.
5 (x – 2y)² + 3 (x – 2y)
Solution:
5 (x – 2y)² + 3 (x – 2y)
= 5 (x – 2y) (x – 2y) + 3 (x – 2y)
= (x – 2y) {5 (x – 2y) + 3}
{(x – 2y) is common}
= (x – 2y) (5x – 10y + 3)

Question 6.
16 (2l – 3m)² – 12 (3m – 2l)
Solution:
16 (2l – 3m)² – 12 (3m-2l)
= 16 (2l – 3m) (2l – 3m) + 12 (2l – 3m)
HCF of 16, 12 = 4 4 (2l-3m) {4 (2l- 3m) + 3}
{(2l – 3m) is common}
= 4 (2l -3m) (8l- 12m+ 3)

Question 7.
3a (x – 2y) – b (x – 2y)
Solution:
3a (x – 2y) – b (x – 2y)
= (x – 2y) (3a – b)
{(x – 2y) is common}

Question 8.
a² (x + y) + b² (x + y) + c² (x + y)
Solution:
a² (x + y) + b² (x + y) + c² (x + 3’)
= (x + y) (a² + b² + c²)
{(x + y) is common}

Question 9.
(x-y)² + (x -y)
Solution:
(x – y)² + (x- y) = (x – y) (x – y) + (x – y)
= (x – y) (x – y + 1)                          {(a – y) is common}

Question 10.
6 (a + 2b) – 4 (a + 2b)²
Solution:
6 (a + 2b) – 4 (a + 2b)²
= 6 (a + 2b) – 4 (a + 2b) (a + 2b)
HCF of 6, 4 = 2
= 2 {a + 2b) {3 – 2 {a + 2b)
{2 (a + b) is common}
= 2 (a + 2b) (3-2 a- 4b)

Question 11.
a (x -y) + 2b (y – x) + c (x -y)²
Solution:
a (x -y) + 2b (y – x) + c (x -y)²
= a (x – y) – 2b (x – y) + c (x – y) {x – y)
= (x – y) {x – 2b + c (x – y)}
{(a – y) is common}
= (a – y) (a – 2b + cx – cy)

Question 12.
– 4 (a – 2y)² + 8 (a – 2y)
Solution:
– 4 (x – 2y)² + 8 (x – 2y)
= – 4 (x – 2y) (x – 2y) + 8 (x – 2y)
{- 4 (x – 2y) is common}
= – 4 (x – 2y) (x – 2y – 2)
= 4 (x – 2y) (2 – x + 2y)

Question 13.
x³ (a – 2b) + a² (a – 2b)
Solution:
x³ (a – 2b) + x² (a – 2b)
HCF of x³, x² = x^2
∴ x² (a – 2b) (x + 1)
{x² (x – 2b) is common}
= x² (x – 2b) (x + 1)

Question 14.
(2x – 3y) (a + b) + (3x – 2y) (a + b)
Solution:
(2x – 3y) (a + b) + (3x – 2y) (a + b)
= (a + b) {2x – 3y + 3x – 2y}
{(x + b) is common}
= (a + b) (5x – 5y)
= 5 (a + b) (x – y)

Question 15.
4 (x + y) (3a – b) + 6 (a + y) (2b – 3a)
Solution:
4 (x + y) (3a – b) + 6 (a + y) (2b – 3a)
= 4 (x + y) (3a – b) – 6 (x + y) (3a – 2b)
HCF of 4, 6 = 2
= 2 (x + y) {2 (3a – b) – 3 (3a – 2b)}
= 2 (x + 3) {6a – 2b – 9a + 6b}
= 2 (x +y) {-3a + 4b}
= 2 (x + y) (4b – 3a)

Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9

Other Exercises

• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.7
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.8
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9

Factorize each of the following quadratic polynomials by using the method of completing the square.
Question 1.
p² + 6p + 8
Solution:
p² + 6p + 8
= p² + 2 x p x 3 + 3² – 3² + 8   (completing the square)
= (p² + 6p + 3²) – 1
= (p + 3)² – 1²
= (P + 3)² – (1)²       { ∵ a² + b²  = (a+b) (a-b)}
= (p +3+1) (p + 3 -1)
= (p+4) (p+ 2)

Question 2.
q² – 10q + 21
Solution:
q² – 10q + 21
= (q)² – 2 x q x 5 + (5)² – (5)² + 21   (completing the square)
= (q)² – 2 x q x 5 + (5)² -25+21
= (q)²-2 x q x 5 + (5)² – 25 +21
= (q)²-2 x q x 5 + (5)² – 4
= (q – 5)² – (2)     {∵ a² – b² = (a + b) (a – b)}
= (q- 5 + 2) (q-5-2)
=(q- 3) (q-7)

Question 3.
4y² + 12y + 5
Solution:
4y² +12y + 5
= (2y)² + 2 x 2y x 3 + (3)² – (3)² + 5    (completing the square)
= (2y + 3)² – 9 + 5
= (2y + 3)² – 4
= (2y + 3)²-(2)²   {∵ a² – b² = (a + b) (a – b)}
= (2y + 3 + 2) (2y + 3 – 2)
= (2y + 5) (2y+ 1)

Question 4.
p² + 6p- 16
Solution:
p² + 6p – 16
= (p)² + 2 x  p x 3 + (3)² – (3)² – 16    (completing the square)
= (p)² + 2 x p x 3 + (3)² – 9 – 16
= (p + 3)² – 25
= (p + 3)² – (5)²     {∵ a² -b² = {a + b) (a – b)}
= (p + 3 + 5)(p + 3-5)
= (p + 8) (p – 2)

Question 5.
x² + 12x + 20
Solution:
x² + 12x + 20
= (x)² + 2 x x x 6 + (6)² – (6)² + 20   (completing the square)
= (x)² + 2 x x x6 + (6)² -36 + 20
= (x + 6)² -16
= (x + 6)² – (4)²   {∵ a² – b² = (a + b) (a – b)}
= (x + 6 + 4) (x + 6 – 4)
= (x + 10) (x + 2)

Question 6.
a² – 14a – 51
Solution:
a² – 14a-51
= (a)² – 2 x x 7 + (7)² – (7)² – 51       (completing the square)
= (a)² – 2 x a x 7 + (7)² – 49 – 51
= (a – 7)² – 100
= (a – 7)² – (10)²    {∵  a² – b² = (a + b) (a – b)}
= (a – 7 + 10) (a – 7 – 10)
= (a + 3) (a – 17)

Question 7.
a² + 2a – 3
Solution:
a² + 2a – 3
= (a)² + 2 x a x 1 + (1)² – (1)2 – 3   (completing the square)
= (a)² + 2 x a x 1 + (1)² – 1 – 3
= (a + 1)² – 4
= (a + 1)² – (2)² {∵ a² – b² = (a + b) (a – b)}
= (a + 1 + 2) (a + 1 – 2)
= (a + 3) (a – 1)

Question 8.
4x² – 12x + 5
Solution:
4x² – 12x + 5
= (2x)² – 2 x 2x x 3 + (3)² – (3)² + 5  (completing the square)
= (2x)² – 2 x 2x x 3 + (3)² -9 + 5
= (2x – 3)² – 4
= (2x – 3)² – (2)²      {∵ a² – b² = (a + b) (a – b)}
= (2x – 3 + 2) (2x – 3 – 2)
= (2x – 1) (2x – 5)

Question 9.
y² – 7y + 12
Solution:

Question 10.
z²-4z-12
Solution:
z² – 4z – 12
= (z)² – 2 x z x 2 + (2)² – (2)² – 12  (completing the square)
= (z)² – 2 x z x 2 + (2)² – 4 – 12
= (z-2)²-16
= (z-2)²-(4)²   {∵ a² – b² = (a + b) (a – b)}
= (z – 2 + 4) (z – 2 – 4)
= (z + 2)(z-6)

Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.7
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.8
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9

Factorize each of the following expressions :
Question 1.
qr-pr + qs – ps
Solution:
qr- pr + qs-ps
Arranging in suitable groups = r(q-p) +s (q-p)    {(q – p) is common}
= (q-p) (r + s)

Question 2.
p²q -pr²-pq + r²
Solution:
p²q -pr²-pq + r2
= p²q -pq-pr² + r² (Arranging in group)
= pq(p- 1)-r²(p-1) {(p – 1) is common}
= (p – 1) (pq – r²)

Question 3.
1 + x + xy + x²y
Solution:
1 + x + xy + x 2y
= 1 (1 + x) +xy (1 +x)
= (1 + x) (1 + xy) {(1 + x) is common}

Question 4.
ax + ay – bx – by
Solution:
ax + ay – bx – by
= a (x + y) – b (x + y)   {(x + y) is coinmon}
= (x+y) (a- b)

Question 5.
xa² + xb² -ya² – yb²
Solution:
xa² + xb² – ya² – yb²
= x (a² + b²) -y (a² + b²)   {(a² + b²) is common}
= {a² + b²) (x -y)

Question 6.
x² + xy + xz + yz
Solution:
x² + xy + xz + yz
= x (x + y) + z(x + y) {(x + y) is common}
= (x + y) (x + z)

Question 7.
2ax + bx + 2ay + by
Solution:
2ax + bx + 2ay + by
= x {2a + b) + y (2a + b)      {(2a + b) is common}
= (2a + b) (x + y)

Question 8.
ab- by- ay +y²
Solution:
ab – by – ay + y²
= b(a-y)-y(a-y)    {(a -y) is common}
= (a-y) (b – y)

Question 9.
axy + bcxy -az- bcz
Solution:
axy + bcxy – az – bcz
= xy (a + bc) – z (a + bc)       {(a + bc) is common}
= (a + bc) (xy – z)

Question 10.
lm² – mn² – lm + n²
Solution:
lm² – mn² – lm + n²
= m (lm – n²)- 1 (lm – n²)  {(lm – n²) is common}
= (lm – n²) (m – 1)

Question 11.
x³ – y² + x – x²y²
Solution:
x³ -y² + x – x²y²
⇒ x³ + x – x²y² – y²
= x(x²+ 1)-y²(x²+ 1)        {(x² + 1) is common}
= (x² + 1) (x -y²)

Question 12.
6xy + 6 – 9y – 4x
Solution:
6xy + 6 – 9y – 4x
= 6 xy – 4x – 9y + 6
= 2x (3y – 2) – 3 (3y – 2)    {(3y – 2) is common}
= (3y-2) (2x – 3)

Question 13.
x² – 2ax – 2ab + bx
Solution:
x² – 2ax – 2ab + bx
⇒ x² – 2ax + bx – 2ab
= x (x – 2a) + b (x – 2a)   {(x – 2a) is common}
= (x – 2a) (x + b)

Question 14.
x³ – 2x²y + 3xy² – 6y³
Solution:
x³ – 2x²y + 3xy² – 6y³
= x² (x – 2y) + 3y² (x – 2y)     {(x – 2y) is common}
= (x – 2y) (x² + 3y²)

Question 15.
abx² + (ay – b) x-y
Solution:
abx² + (ay – b) x-y
= abx² + ayx – bx -y 
= ax (bx + y) – 1 (bx + y)               {(bx +y) is common}
= (bx + y) (ax – 1)

Question 16.
(ax + by)² + (bx – ay)²
Solution:
(ax + by)² + (bx – ay)²
= a²x² + b²y² + 2abxy + b²x² + a²y² – 2abxy
= a²x² + b²y² + b²x² + a²y²
= a²x² + b²x² + a²y² + by²
= x² (a² + b²) + y² (a² + b²)         {(a² + b²) is common}
= (a² + b²) (x² + y²)

Question 17.
16 (a – b)³ -24 (a- b)²
Solution:
16 (a – b)³ -24 (a- b)²
HCF of 16, 24 = 8
and HCF of (a – b)³, (a – b)² = (a – b)²
∴16 (a – b)³ – 24 (a – b)²
= 8 (a-b)² {2 (a-b)- 3}
{8 (a – b)² is common}
= 8 (a – b)² (2a – 2b – 3)

Question 18.
ab (x² + 1) + x (a² + b²)
Solution:
ab (x² + 1) + x (a² + b²)
= abx² + ab + a²x + b²x
= abx² + b²x + a²x + ab
= bx (ax + b) + a (ax + b)  {(ax + b) is common}
= (ax + b) (bx + a)

Question 19.
a²x² + (ax² + 1) x + a
Solution:
a²x² + (ax² + 1) x + a
= a²x² + ax³ + x + a
= ax³ + a²x² + x + a
= ax² (x + a) + 1 (x + a) {(x + a) is common}
= (x + a) (ax² + 1)

Question 20.
a(a- 2b -c) + 2bc
Solution:
a(a- 2b -c) + 2bc
= a²– 2ab -ac +2bc
= a (a – 2b) – c (a – 2b) {(a – 2b) is common}
= (a – 2b) (a – c)

Question 21.
a (a + b – c)- bc
Solution:
a (a + b – c) – bc
= a² + ab – ac – bc
= a (a + b) – c (a + b)   {(a + b) is common}
= (a + b) (a – c)

Question 22.
x² – 11xy – x +11y
Solution:
x² – 11xy-x + 11y
= x² -x – 11 xy + 11 y
= x (x – 1) – 11y (x – 1)   {(x – 1) is common}
= (x- 1) (x- 11y)

Question 23.
ab – a – b + 1
Solution:
ab – a-b + 1
= a (b – 1) – 1 (b – 1)    {(b – 1) is common}
= (b – 1) (a – 1)

Question 24.
x² + y – xy – x
Solution:
x² + y – xy – x
= x² – x- xy + y
= x (x – 1) – y (x – 1)   {(x – 1) is common}
= (x- 1) (x-y)

Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4

Other Exercises

• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.2
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.3
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4

Question 1.
Four-fifth of a number is more than three-fourth of the number by 4. Find the number.
Solution:
Let the required number = x
Then four-fifth of the number = \(\frac { 4 }{ 5 }\)x
and three- fourth =  \(\frac { 3 }{ 4 }\)x

Question 2.
The difference between the squares of two consecutive numbers is 31. Find the numbers.
Solution:
Let first number = x
There second number = x + 1
∴ According to the condition :
(x + 1)² – (x)² = 31
⇒ x² + 2x + 1 – x² = 31
⇒ 2x = 31 – 1 = 30 30
⇒ x =  \(\frac { 30 }{ 2 }\) = 15
∴  First number = 15
and second number = 15 + 1 = 16
Hence numbers are 15, 16
Check : (16)² – (15)² = 256 – 225 = 31
Which is given
∴  Our answer is correct.

Question 3.
Find a number whose double is 45 greater than its half.
Solution:
Let the required number = x
Double of it = 2x
and half of it =  \(\frac { x }{ 2 }\)
According to the condition :

Question 4.
Find a number such that when 5 is subtracted from 5 times the number, the result is 4 more than twice the number.
Solution:
Let the required number = x 5
times of it = 5x
twice of it = 2x
According to the condition :
5x – 5 = 2x + 4
⇒ 5x – 2x = 4 + 5
⇒ 3x = 9
⇒ x =\(\frac { 9 }{ 3 }\)   = 3
Required number = 3
Check :3 x 5-5 = 2×3+4
⇒  15-5 = 6 + 4
⇒ 10= 10
Which is true. Therefore our answer is correct.

Question 5.
A number whose fifth part increased by 5 is equal to its fourth part diminished by 5. Find the number.
Solution:
Let the number = x
Then fifth part increased by 5 = \(\frac { x }{ 5 }\) + 5
Fourth part diminished by 5 = \(\frac { x }{ 4 }\)  – 5
According to the condition :

Question 6.
A number consists of two digits whose sum is 9. If 27 is subtracted from the number, its digits are reversed. Find the number.
Solution:
Sum of two digits = 9
Let units digit = x
Then tens digit = 9 – x
and number = 10 (9 – x) + x
= 90 – 10x + x = 90 -9x
On reversing the digits,
Units digit = 9 -x tens digit = x
and number = 10 (x) + 9 – x
= 10x + 9- x = 9x + 9
According to the condition :
90 – 9x – 27 = 9x + 9
⇒ 9x + 9x = 90 – 27-9
⇒ 18x = 90- 36 = 54
⇒ x =\(\frac { 54 }{ 18 }\) = 3
Number = 90 – 9x = 90 – 9 x 3 = 90 – 27 = 63
Check : 63 – 27 = 36 (Whose digits are reversed)
Which is true. Therefore our answer is correct.

Question 7.
Divide 184 into two parts such that one- third of one part may exceed one seventh of another part by 8.
Solution:
Sum of two parts = 184
Let first part = x
Then second part = 184 – x
According to the condition :

Question 8.
The numerator of a fraction is 6 less than the denominator. If 3 is added to the numerator, the fraction is equal to \(\frac { 2 }{ 3 }\) . What is the original fraction equal to ?
Solution:
Let denominator of the original fraction = x
Then numerator = x – 6
and fraction = \(\frac { x-6 }{ x }\)
According to the condition :

Question 9.
A sum of Rs. 800 is in the form of denominations of Rs. 10 and Rs. 20. If the total number of notes be 50, find the number of notes of each type.
Solution:
Total amount = Rs. 800
Total number of notes = 50
Let number of notes of Rs. 10 = x
Then number of notes of Rs. 20 = 50 – x
According to the condition, x x 10 + (50-x) x 20 = 800
⇒  10x + 1000 – 20x = 800
⇒  -10x = 800- 1000 = -200
⇒ x =   \(\frac { -200 }{ -10 }\) = 20
∴ Number of 10-rupees notes = 20
and number of 20-rupees notes = 50-20 = 30
Check : 20 x 10 + 30 x 20
= 200 + 600 = 800
Which is true. Therefore our answer is correct.

Question 10.
Seeta Devi has Rs. 9 in fifty-paise and twenty five-paise coins. She has twice as many twenty-five paise coins as she has fifty-paise coins. How many coins of each kind does she have ?
Solution:
Total amount = Rs. 9
Let fifty paise coins = x
Then twenty-five paise coins = 2x
According to the condition :

Question 11.
Sunita is twice as old as Ashima. If six years is subtracted from Ashima’s age and four years added to Sunita’s age, then Sunita will be four times Ashima’s age. How old were they two years ago ?
Solution:
Let age of Ashima = x
Then age of Sunita = 2x
According to the condition :
4 (x – 6) = 2x + 4
⇒  4x-24 = 2x + 4
⇒ 4x-2x = 4 + 24
⇒  2x = 28
⇒ x = \(\frac { 28 }{ 2 }\) = 14
∴  Sunita’s present age = 2x = 2 x 14 = 28 years
and Ashima’s age = 14 years
Two years ago,
Age of Sunita = 28 – 2 = 26 years
and age of Ashima =14-2 = 12 years

Question 12.
The ages of Sonu and Monu are in the ratio 7 : 5. Ten years hence, the ratio of their ages will be 9 : 7. Find their present ages.
Solution:
Ratio in the present ages of Sonu and Monu = 7:5
Let age of Sonu = 7x years
and age of Monu = 5x years
10 years hence,
the age of Sonu = 7x + 10 years
and age of Monu = 5a + 10 years
According to the condition :

Question 13.
Five years ago a man was seven times as old as his son. Five years hence, the father will be three times as old as his son. Find their present ages.
Solution:
5 years ago,
Let age of son = x years
Then, age of father = 7a years
Present age of son = x + 5 years
and age of father = 7x + 5 years
5 years hence,
age of son = x + 5 + 5= x+10
and age of father = 7x + 5 + 5 = 7x + 10
According to the condition :
7x + 10 = 3 (x + 10)
⇒  7x + 10 = 3x + 30
⇒  7x -3x= 30 – 10 = 20

Question 14.
I am currently 5 times as old as my son. In 6 years time I will be three times as old as he will be then. What are our ages now ?
Solution:
Let present age of my son = x years
Then my age = 5x years
After 6 years,
my age will be = 5x + 6
and my son’s age = x + 6
According to the condition
5x + 6 = 3 (x + 6)
⇒ 5x+ 6 = 3x+ 18
⇒ 5x – 3x = 18 – 6 ⇒ 2x = 12
⇒ x = 6
∴ Present my age = 5x = 5 x 6 = 30 years
and my son’s age = 6 years

Question 15.
I have Rs. 1000 in ten and five rupees notes. If the number of ten rupees notes that I have is ten more than the number of five rupees notes, how many notes do I have in each denomination ?
Solution:
Total amount = Rs. 1000
Let the number of five rupee notes = x
∴ Ten rupees notes = x + 10
According to the condition,
(x + 10) x 10 + 5 x x x = 1000
⇒ 10a + 100 + 5a = 1000
⇒  15a = 1000- 100 = 900
⇒ x = \(\frac { 900 }{ 15 }\) = 60
∴  Number of five rupees notes = 60
and number of ten rupees notes = 60 + 10 = 70

Question 16.
At a party, colas, squash anjd fruit juice were offered to guests. A fourth of the guests drank colas, a third drank squash, two fifths drank juice and just three did not drink any thing. How many guests were in all ?
Solution:
Let total number of guests = x
Guests who drank colas = \(\frac { x }{ 4 }\)
Guests who drank squash = \(\frac { x }{ 3 }\)
Guests who drank juice = \(\frac { 2 }{ 5 }\) x
Guest who drank none of these = 3
According to the condition :

Question 17.
There are 180 multiple choice questions in a test. If a candidate gets 4 marks for every correct answer and for every unattempted or wrongly answered question one mark is deducted from the total score of correct answers. If a candidate scored 450 marks in the test, how many questions did he answer correctly ?
Solution:
Number of total questions = 180
Let the candidate answers questions correctly = x
∴ Uncorrect or unattended questions =180 -x
total score he got = 450
According to the condition
x x 4-(180-x) x 1 =450
⇒ 4x – 180 + x = 450
⇒ 5x = 450+ 180 = 630
⇒ x =\(\frac { 630 }{ 5 }\) = 126
Number of question which answered correctly = 126

Question 18.
A labourer is engaged for 20 days on the condition that he will receive Rs. 60 for each day, he works and he will be fined Rs. 5 for each day, he is absent, If he receives Rs. 745 in all, for how many days he remained absent ?
Solution:
Total number of days = 20
Let number of days he worked = x
Then number of days he remained absent = 20 – x
According to the condition :
x x 60 – (20 – x) x 5 = 745
⇒  60x- 100 + 5x = 745
⇒  65x = 745 + 100 = 845
⇒  x = \(\frac { 845 }{ 65 }\) = 13
∴ Number of days he worked =13 days
and number of days he remained absent = 20 – 13 = 7 days.

Question 19.
Ravish has three boxes whose total weight is 60 \(\frac { 1 }{ 2 }\) kg. Box B weighs 3\(\frac { 1 }{ 2 }\) kg more it than A and box C weighs 5\(\frac { 1 }{ 3 }\) kg more than box B. Find the weight of box A.
Solution:
Total weight of three boxes = 60\(\frac { 1 }{ 2 }\) kg.
Let weight of box A = x kg.

Question 20.
The numerator of a rational number is 3 less than the denominator. If the denominator is increased by 5 and the numerator by 2, we get the rational number \(\frac { 1 }{ 2 }\). Find the rational number.
Solution:
Let denominator of the given rational number = x
Then numerator = x – 3
∴ Rational number =\(\frac { x – 3 }{ x }\)
According to the condition :

Question 21.
In a rational number, twice the numerator is 2 more than the denominator. If 3 is added to each, the numerator and the denominator, the new fraction is \(\frac { 2 }{ 3 }\) . Find the original number.
Solution:

Question 22.
The distance between two stations is 340 km. Two trains start simultaneously from these stations on parallel tracks to cross each other. The speed of one of them is greater than that of the other by 5 km/ hr. If the distance between the two trains after 2 hours of their start is 30 km, find the speed of each train.
Solution:
Distance between two stations = 340 km.
Let the speed of the first train = x km/hr.
Then speed of second train = (x + 5) km/h.
Time = 2 hours
Distance travelled by the first train in 2 hours = 2x km
and distance travelled by the second train = 2 (x + 5) km
According to the condition,

Question 23.
A steamer goes downstream from one point to another in 9 hours. It covers the same distance upstream in 10 hours. If the speed of the stream be 1 km/hr, find the speed of the steamer in still water and the distance between the ports.
Solution:
Time taken by a steamer downstream = 9 hours
and upstream = 10 hours Speed of steamer = 1 km/hr.
Let speed of the steamer = x km/h.
According to the condition :
9 (x + 1) = 10 (x – 1)
9x + 9 = 10x – 10 ⇒ 10x – 9x = 9 + 10
⇒ x = 19
∴  Speed of steamer in still water =19 km/h
and distance between two ports = 9 (a + 1) = 9 (19 + 1) = 9 x 20 = 180 km.

Question 24.
Bhagwanti inherited Rs. 12000.00 She invested part of it as 10% and the rest at 12%. Her annual income from these investments is Rs. 1280.00. How much did she invest at each rate ?
Solution:
Total investment = Rs. 12000.00
Rate of interest for first part = 10%
and for second part = 12%
Annual income = Rs. 1280.00
Let the investment for the first part = Rs. x
and second part = Rs. (12000 – x)
According to the condition :

Question 25.
Total investment = Rs. 12000.00 Rate of interest for first part = 10% and for second part = 12% Annual income = Rs. 1280.00 Let the investment for the first part = Rs. a and second part = Rs. (12000 – a) According to the condition :
Solution:
Let breadth of the rectangle = x cm
Then length = (x + 9) cm
∴ Area = length x breadth = x (x + 9) cm²
By increasing each length and breadth by 3 cm
The new length of the rectangle = x + 9 + 3
= (x + 12) cm
and breadth = (x + 3) cm
∴  Area = (x + 12) (x + 3)
According to the condition :
(x + 12) (x + 3) – a (x + 9) = 84
x² + 3x + 12x + 36 – x² – 9x = 84
⇒ 6a = 84 – 36 = 48 ⇒ x  = \(\frac { 48 }{ 6 }\) =8
∴  Length of the rectangle = a + 9 = 8 + 9 = 17 cm
and breadth =x = 8 cm.

Question 26.
The sum of the ages of Anup and his father is 100. When Anup is as old as his father now, he will be five times as old as his son Anuj is now. Anuj will be eight years older than Anup is now, when Anup is as old as his father. What are their ages now ?
Solution:
Sum of ages of Anup and his father =100 years
Let present age of Anup = x years
∴  Age of his father = (100 – x) years
∴  Age of Anuj = \(\frac { 100 – x  }{ 5 }\) years
and also Anuj’s age = (x + 8) years ….I
Anup becomes as old as his father is now
after (100 – 2x) years
∴ After (100 – 2x) years

Question 27.
A lady went shopping and spent half of what she had on buying hankies and gave a rupee to a begger waiting outside the shop. She spent half of what was left on a lunch and followed that up with a two rupee tip. She spent half of the remaining amount on a book and three rupees on bus fare. When she reached home, she found that she had exactly one rupee left. How much money did she start with ?
Solution:
Let the amount, a lady has in the beginning = Rs. x

Hope given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.1
• RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.2
• RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.3
• RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.4
• RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.5
• RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.6

Question 1.
5x³ – 15x² + 25x by 5x
Solution:

Question 2.
4z³ + 6z²-zby \(\frac { -1 }{ 2 }\) z
Solution:

Question 3.
9x²y – 6xy + 12xy² by \(\frac { -3 }{ 2 }\) xy
Solution:

Question 4.
3x²y² + 2x²y + 15xy by 3xy
Solution:

Question 5.
x² + 7x + 12 by x + 4
Solution:

Question 6.
4y² 4 + 3y + \(\frac { -1 }{ 2 }\) by 2y + 1
Solution:

Question 7.
3x³ + 4x² + 5x + 18 by x + 2
Solution:

Question 8.
14x² – 53x + 45 by 7a – 9
Solution:

Question 9.
-21 + 71x – 31x² – 24ax³ by 3 – 8ax
Solution:

Question 10.
3y⁴ – 3y³ – 4y² – 4y by y² – 2y
Solution:

Question 11.
2y⁵ + 10y⁴ + 6y³ + y² + 5y + 3 by 2y³ + 1
Solution:

Question 12.
x⁴ – 2x³ + 2x² + x + 4 by x² + x + 1
Solution:

Question 13.
m³ – 14m² + 37m – 26 by m² – 12m + 13
Solution:

Question 14.
x⁴ + x² + 1 by x² + x + 1
Solution:

Question 15.
x⁵ + x⁴ + x³+x² + x+ 1 by x³ + 1
Solution:

Divide each of the following and find the quotient and remainder :

Question 16.
14x³ – 5x² + 9x -1 by 2x – 1
Solution:

Question 17.
6x³ – x² – 10x – 3 by 2x – 3
Solution:

Question 18.
6x³+ 11x² – 39x – 65 by 3x² + 13x + 13
Solution:

Question 19.
30a⁴ + 11a³-82a²– 12a + 48 by 3a² + 2a- 4
Solution:

Question 20.
9x⁴ – 4x² + 4 by 3x² – 4x + 2
Solution:

Question 21.
Verify division algorithm i.e., Dividend = Divisor * Quotient + Remainder, in each of the following. Also, write the quotient and remainder :

Solution:

Question 22.
Divide 15y⁴ + 16y³ + \(\frac { 10 }{ 3 }\) y – 9y² – 6 by 3y – 2
Write down the co-efficients of the terms in the quotient.
Solution:

Question 23.
Using division of polynomials state whether.
(i) x + 6 is a factor of x² – x – 42
(ii) 4x – 1 is a factor of 4x² – 13x – 12
(iii) 2y – 5 is a factor of 4y⁴ – 10y³ – 10y² + 30y -15
(iv) 3y + 5 is a factor of 6y⁵ + 15y + 16y + 4y+ 10y – 35
(v) z² + 3 is a factor of z⁵– 9z
(vi) 2x² – x + 3 is a factor of 60x⁵-x⁴ + 4x³ – 5x² -x- 15
Solution:

Question 24.
Find the value of ‘a’, if x + 2 is a factor of 4x⁴ + 2x³ – 3x² + 8x + 5a.
Solution:

Question 25.
What must be added to x⁴ + 2x³ — 2x² + x – 1 so that the resulting polynomial is exactly divisible by x² + 2x – 3.
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 8 Division of Algebraic Expressions Ex 8.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.2

Other Exercises

• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.2
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.3
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4

Solve each of the following equations and also check your result in each case :
Question 1.
\(\frac { 2x + 5 }{ 3 }\) = 3x – 10
Solution:
\(\frac { 2x + 5 }{ 3 }\) = \(\frac { 3x – 10 }{ 1 }\)
By cross multiplication
⇒ 2x + 5 = 3 (3x – 10)
⇒ 2x + 5 = 9x – 30
⇒ 5 + 30 = 9x – 2x (By transposition)
⇒ 35 = 7x
⇒ x = 5

Question 2.
\(\frac { a – 8 }{ 3 }\) = \(\frac { a – 3 }{ 2 }\)
Solution:

Question 3.
\(\frac { 7y + 2 }{ 5 }\) = \(\frac { 6y – 5 }{ 11 }\)
Solution:

Question 4.
x – 2x + 2 – \(\frac { 16 }{ 3 }\) x + 5 = 3 – \(\frac { 7 }{ 2 }\) x.
Solution:

Question 5.
\(\frac { 1 }{ 2 }\) x + 7x – 6 = 7x + \(\frac { 1 }{ 4 }\)
Solution:

Question 6.
\(\frac { 3 }{ 4 }\) x + 4x = \(\frac { 7 }{ 8 }\) + 6x – 6
Solution:

Question 7.
\(\frac { 7 }{ 2 }\) x – \(\frac { 5 }{ 2 }\) x = \(\frac { 20 }{ 3 }\) x + 10
Solution:
\(\frac { 7 }{ 2 }\) x – \(\frac { 5 }{ 2 }\) x = \(\frac { 20 }{ 3 }\) x + 10

Question 8.
\(\frac { 6x + 1 }{ 2 }\) + 1 = \(\frac { 7x – 3 }{ 3 }\)
Solution:

Question 9.
\(\frac { 3a – 2 }{ 3 }\) + \(\frac { 2a + 3 }{ 2 }\) = a + \(\frac { 7 }{ 6 }\)
Solution:

Question 10.
x – \(\frac { x – 1 }{ 2 }\) = 1 – \(\frac { x – 2 }{ 3 }\)
Solution:

Question 11.
\(\frac { 3x }{ 4 }\) – \(\frac { x – 1 }{ 2 }\) = \(\frac { x – 2 }{ 3 }\)
Solution:

Question 12.
\(\frac { 5x }{ 3 }\) – \(\frac { x – 1 }{ 4 }\) = \(\frac { x – 3 }{ 5 }\)
Solution:
\(\frac { 5x }{ 3 }\) – \(\frac { x – 1 }{ 4 }\) = \(\frac { x – 3 }{ 5 }\)

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.
0.18 (5x – 4) = 0.5x + 0.8
Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21.

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.
(3x – 8) (3x + 2) – (4x – 11) (2x + 1) = (x – 3) (x + 7)
Solution:
(3x – 8) (3x + 2) – (4x – 11) (2x + 1) = (x – 3) (x + 7)
⇒ (9x² + 6x – 24x – 16) – (8x² + 4x – 22x – 11) = x² + 7x – 3x – 21
⇒ 9x² + 6x – 24x – 16 – 8x² – 4x + 22x + 11 = x² + 4x – 21
⇒ 9x² – 8x² – x² + 6x – 24x + 22x – 4x – 4x = -21 + 16 – 11
⇒ 28x – 32x = -32 + 16
⇒ -4x = -16
⇒ x = 4
Verification:
L.H.S. = (3x – 8) (3x + 2) – (4x – 11) (2x + 1)
= (3 x 4 – 8) (3 x 4 + 2) – (4 x 4 – 11) (2 x 4 + 1)
= (12 – 8) (12 + 2) – (16 – 11) (8 + 1)
= 4 x 14 – 5 x 9 = 56 – 45 = 11
R.H.S. = (x – 3) (x + 7) = (4 – 3) (4 + 7) = 1 x 11 = 11
L.H.S. = R.H.S.

Question 25.
[(2x + 3) + (x + 5)]² + [(2x + 3) – (x + 5)]² = 10x² + 92
Solution:
[(2x + 3) + (x + 5)]² + [(2x + 3) – (x + 5)]² = 10x² + 92
⇒ (2x + 3 + x + 5)² + (2x + 3 – x – 5)² = 10x² + 92
⇒ (3x + 8)² + (x – 2)² = 10x² + 92
⇒ 9x² + 2 x 3x x 8 + 64 + x² – 2 x x x 2 + 4 = 10x² + 92
⇒ 9x² + 48x + 64 + x² – 4x + 4 = 10x² + 92
⇒ 9x² + x² – 10x² + 48x – 4x = 92 – 64 – 4
⇒ 44x = 24

Hope given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 7 Factorization Ex 7.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.7
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.8
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9

Factorize the following :

Question 1.
3x-9
Solution:
3x – 9 = 3 (x – 3)        (HCF of 3, 9 = 3)

Question 2.
5x – 15x²
Solution:
5x- 15x² = 5x (1 – 3x)
{HCF of 5, 15 = 5 and of x, x² = x}

Question 3.
20a¹²b² – 15a⁸b⁴
Solution:
20a¹²b² – 15a⁸b⁴
{HCF of 20, 15 = 5, a¹², a⁸ = a⁸, b², b⁴ = b²}
= 5a⁸ b²(4a⁴ – 3b²)

Question 4.
72xy – 96x⁷y⁶
Solution:
72xy – 96x⁷y⁶
HCF of 72, 96 = 24 of x⁶x⁷ = x⁶, y⁷,y⁶ = y⁶
∴ 72x⁷y⁶ – 96x⁷y⁶ = 24x⁶y⁶ (3y – 4x)

Question 5.
20X³ – 40x² + 80x
Solution:
20x³ – 40x² + 80x
HCF of 20, 40,80 = 20
HCF of x³, x², x = x
∴ 20x³ – 40x² + 80x = 20x (x² – 2x + 4)

Question 6.
2x³y² – 4x²y³ + 8xy⁴
Solution:
2x³y² – 4x²y³ + 8xy⁴
HCF of 2, 4, 8 = 2
HCF of x³, x², x = 1
and HCF of y², y³, y⁴ = y²
∴ 2x³y² – 4x²y³ + 8xy⁴
= 2xy² (x² – 2xy + 4y²)

Question 7.
10m³n² + 15m⁴n – 20m²n³
Solution:
10m³n² + 15m⁴n – 20m²n³
HCF of 10, 15, 20 = 5
HCF of m³, m⁴, m² = m²
HCF of n², n, n³ = n
10m³n² + 15m⁴n – 20m²n³
5m²n(2mn + 3m²– 4n²)

Question 8.
2a⁴b⁴ – 3a³b⁵ + 4a²b⁵
Solution:
2a⁴b⁴ – 3a³b⁵ + 4a²b⁵
HCF of 2, 3, 4= 1
HCF of a⁴, a³, a² = a²
HCF of b⁴, b⁵ b⁵ = b⁴
∴ 2a⁴b⁴ – 3a³b⁵ + 4a²b⁵ = a²b⁴
(2a² – 3ab + 4b)

Question 9.
28a² + 14a²b² – 21a⁴
Solution:
28a² + 14a²b² – 21a⁴
HCF of 28, 14,21 =7
HCF of a², a², a⁴ = a²
HCF of 1, b², 1 = 1
∴ 28a² + 14a²b²-21a⁴ = 7a²
(4 + 2b² – 3a²)

Question 10.
a⁴b – 3a²b² – 6ab³
Solution:
a⁴b – 3a²b² – 6ab³
HCF of 1,3,6 = 1
HCF of a⁴, a², a = a
HCF of b, b², b³ = b
∴ a⁴b – 3a²b² – 6ab³ = ab (a³ – 3ab – 6b²)

Question 11.
2l²mn – 3lm²n + 4lmn²
Solution:
2l²mn – 3lm²n + 4lmn²
HCF 2, 3,4 = 1,
HCF of l²,l,l = l
HCF of m, m², m = m
HCF of n, n, n² = n
∴ 2l² mn – 3lm²n + 4lmn²
= lmn (21 -3m + 4n)

Question 12.
x⁴y² – x²y⁴ – x⁴y⁴
Solution:
x⁴y² – x²y⁴ – x⁴y⁴
HCF of x⁴, x², x⁴ = x²
HCF of y², y⁴, y⁴ =y²
∴ x⁴y² – x²y⁴ – x⁴y⁴ = x²y² (x² -y² -x²y²)

Question 13.
9 x²y + 3 axy
Solution:
9 x²y + 3 axy
HCF of 9, 3 = 3
HCF of x², x = x
HCF of y,y = y
HCF of 1,a = 1
∴ 9x²y + 3axy = 3xy (3x + a)

Question 14.
16m – 4m²
Solution:
16m – 4m²
HCF of 16, 4 = 4
HCF of m, m² = m
∴ 16m – 4m² = 4m (4 – m)

Question 15.
-4a² + 4ab – 4ca
Solution:
-4a² + 4ab – 4ca
HCF of 4, 4, 4 = 4
HCF of a², a, a = a
∴ -4a² + 4ab – 4ca = -4a (a – b + c)

Question 16.
^{x2yz + xy2z + xyz2}
Solution:
x²yz + xy²z + xyz²
HCF of x², x, x = x
HCF of y,y²,y=y
HCF of z, z,z² = z
∴ x²yz + xy²z + xyz² = xyz (x + y + z)

Question 17.
ax²y + bxy² + cxyz
Solution:
ax²y + bxy² + cxyz
HCF of x², x, x = x,
HCF of y,y²,y = y
ax²y + bxy² + cxyz = xy (ax + by + cz)

Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 7 Factorization Ex 7.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.7
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.8
• RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9

Find the greatest common factors (GCF / HCF) of the following polynomials : (1 – 14)

Question 1.
2x² and 12x²
Solution:
2x² and 12x²
HCF of 2 and 12 =2
HCF of x²,x²=x²
∴ HCF = 2x²

Question 2.
(6xy³ and 18x²y³
Solution:
6x³y and 18xy
HCF of 6, 18 = 6
HCF of x³ and x² = x²
HCF of y and y³ -y
∴ HCF = 6x²y

Question 3.
7x, 21x² and 14xy²
Solution:
7x, 21x² and 14xy²
HCF of 7, 21 and 14 = 7
HCF of x, x², x = x
∴ HCF = 7x

Question 4.
42x²yz and 63x³y²z³
Solution:
42x²yz and 63x³y²z³
HCF of 42 and 63 = 21
HCF of x², x³ = x²
HCF of y,y²=y
HCF of z,z³ = z
∴ HCF = 21 x²yz

Question 5.
12ax²,6a²x³ and 2a³ x⁵
Solution:
12ax², 6a²x³ and 2a³x⁵
HCF of 12, 6,2 = 2
HCF of a, a², a³ = a
HCF of x², x³, x⁵ = x²
∴ HCF = 2ax²

Question 6.
9x², 15x²y³, 6xy² and 21x²y²
Solution:
9x², 15xV, 6xy² and 21x²y²
HCF of 9, 15, 6,21 = 3
HCF of x², x², x, x² = x
HCF of 1, y³, y², y² =2
∴ HCF = 3x

Question 7.
4a²b³ -12a³b, 18a⁴b³
Solution:
4a²b³, -12a³b, 18a⁴b³
HCF of 4, 12, 18 = 2
HCF of a², a³, a⁴ = a²
HCF of b³,b, b³ = b
∴ HCF = 2a²b

Question 8.
6x²y², 9xy³, 3x³y²
Solution:
6x²y², 9xy³, 3x³y²
HCF of 6, 9, 3 = 3
HCF of x², x, x³ = x
HCF of y²,y³,y²=y²
∴ HCF = 3xy²

Question 9.
a²b³, a³b²
Solution:
a²b³, a³b²
HCF of a², a³ = a²
HCF of b³, b² = b²
∴ HCF = a²b²

Question 10.
36a²b²c⁴, 54a⁵c²,90a⁴b²c²
Solution:
36a²b²c⁴, 54a⁵c²,90a⁴b²c²
HCF of 36, 54, 90 = 18
HCF of a², a⁵, a⁴ = a²
HCF of b², 1,b²= 1
HCF of c⁴,c²,c² = c²
∴ HCF = 18a² x 1 x c² = 18a²c²

Question 11.
x³, – yx²
Solution:
x³, – yx²
HCF of x³, x² = x²
HCF of 1, y= 1
∴ HCF = x²

Question 12.
15a³, -45a², -150a
Solution:
15a³,-45a²,-150a
HCF of 15,45, 150 = 15
HCF of a³, a², a = a
∴ HCF = 15a

Question 13.
2x³y², 10x²y³, 14xy
Solution:
2x³y², 10x²y³, 14xy
HCF of 2, 10, 14 = 2
HCF of x³, x², x = x
HCF of y²,y³,y=y
∴ HCF = 2xy

Question 14.
14x³y⁵, 10x⁵y³, 2x²y²
Solution:
14x³y⁵, 10x⁵y³, 2x²y²
HCF of 14, 10, 2, = 2
HCF of x³, x⁵, x² = x²
HCF of y⁵,y³,y²=y²
∴ HCF = 2xy

Find the greatest common factor of the terms in each of the following expressions:

Question 15.
5a⁴ + 10a³ – 15a²
Solution:
5a⁴ + 10a³– 15a²
HCF of 5, 10, 15 = 5
HCF of a⁴, a³, a² = a²
∴ HCF = 5a²

Question 16.
2xyz + 3x²y + 4y²
Solution:
2xyz + 3x²y + 4y²
HCF of 2, 3,4 = 1
HCF of x, x², 1 = 1
HCF of y,y,y² =y
HCF of z, 1, 1 = 1
∴ HCF = y

Question 17.
3a²b² + 4b²c² + 12a²b²c²
Solution:
3a²b² + 4b²c² + 12a²b²c²
HCF of 3, 4, 12 = 1
HCF of a², 1, a² = 1
HCF of b², b², b² = b²
HCF of 1, c², c² = 1
∴ HCF = b²

 

Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 20 Mensuration I (Area of a Trapezium and a Polygon) Ex 20.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3

Question 1.
Find the area of the pentagon shown in the figure if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm and BF = 5 cm, CG = 7 cm and EH = 3

Solution:
In the figure, here are three triangles and one trapezium.

Question 2.
Find the area enclosed by each of the following figures as the sum of the areas of a rectangle and a trapezium:

Solution:
(i) In the figure ABCDEF,
Join CF, then, the figure consists one square and one trapezium ABCF is a square whose side = 18 cm

Area of the square = 18 x 18 cm² = 324 cm²
Area of trapezium FCDE = \(\frac { 1 }{ 2 }\) (CF + ED) x 8 cm²
= \(\frac { 1 }{ 2 }\) (18 + 7) x 8
= \(\frac { 1 }{ 2 }\) x 25 x 8 cm²
= 100 cm²
Total area of fig. ABCDEF = 324 + 100 = 424 cm²
(ii) In the figure ABCDEF,
Join BE.
The figure consists of one rectangle BCDE and one trapezium ABEF

Area of rectangle BCDE = BC x CD = 20 x 15 = 300 cm²
Area of trapezium ABEF,
= \(\frac { 1 }{ 2 }\) (BE + AF) x height
= \(\frac { 1 }{ 2 }\) (15 + 6) x 8 cm²
= \(\frac { 1 }{ 2 }\) x 21 x 8 cm²
= 84 cm²
Area of the figure ABCDEF = 300 + 84 = 384 cm²
(iii) In the figure ABCDEFGH,

HC= AB = EF = 6 cm
AH = BC = 4 cm
DE = GF = 5 cm
Join HC.
In right ∆CDE,
ED² = CD² + CE²
⇒ (5)² = (4)² + (CE)²
⇒ 25 = 16 + (CE)²
⇒ (CE)² = 25 – 16 = 9 = (3)²
CE = 3 cm
The figure consist a rectangle and a trapezium
Area of rectangle ABCH = AB x BC = 6 x 4 = 24 cm²
Area of trapezium GDEF,
= \(\frac { 1 }{ 2 }\) (GD + EF) x CE 1
= \(\frac { 1 }{ 2 }\) (GH + HC + CD + EF) x CE
= \(\frac { 1 }{ 2 }\) (4 + 6 + 4 + 6) x 3 cm²
= \(\frac { 1 }{ 2 }\) x 20 x 3 cm²
= 30 cm²
Total area of the figure ABCDEFGH = 24 + 30 = 54 cm²

Question 3.
There is a pentagonal shaped park as shown in the figure. Jyoti and Kavita divided it in two different ways.


Find the area of this park using both ways. Can you suggest some another way of finding its area ?
Solution:
In first case, the figure ABCDE is divided into 2 trapezium of equal area.
Now area of trapezium DFBC

Total area of the pentagon ABCDE = 2 x 168.75 = 337.5 m²
In second case, the figure ABCDE is divided into two parts, namely one square and other triangle.

Total area of pentagon ABCDE = 225 + 112.5 = 337.5 m²

Question 4.
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.

Solution:
In the figure ABCDEF,
AD = 90 cm
BL = 30 cm
AO = 60 cm
CN = 40 cm
AN = 50 cm
EO = 60 cm
AM = 20 cm
FM = 20 cm
AL = 10 cm



Area of ABCDEF = (150 + 800 + 900 + 200 + 1400 + 1600) cm² = 5050 cm²

Question 5.
Find the area of the following regular hexagon:

Solution:
In the regular hexagon MNOPQR There are two triangles and one rectangle.
Join MQ, MO and RP
NQ = 23 cm,
NA = BQ = \(\frac { 10 }{ 2 }\) = 5 cm
MR = OP = 13 cm

In right ∆BDQ,
PQ² = BQ² + BP²
⇒ (13)² = (5)² + BP²
⇒ 169 = 25 + BP²
⇒ BP² = 169 – 25 = 144 = (12)²
BP = 12 cm
PR = MO = 2 x 12 = 24 cm
Now area of rectangle RPOM = RP x PO = 24 x 13 = 312 cm²
Area of ∆PRQ = \(\frac { 1 }{ 2 }\) x PR x BQ
= \(\frac { 1 }{ 2 }\) x 24 x 5 = 60 cm²
Similarly area ∆MON = 60 cm²
Area of the hexagon MNOPQR = 312 + 60 + 60 = 432 cm²

Hope given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Find the following products 

Question 1.
2a³ (3a + 5b)
Solution:
2a³ (3a + 5b) = 2a³ x 3a + 2a³ x 5b
= 6a^{3 +1} + 10a³b
= 6a⁴ + 10a³b

Question 2.
-11a (3a + 2b)
Solution:
-11a (3a + 2b) = -11a x 3a – 11a x 2b
= -33a²– 22ab

Question 3.
-5a (7a – 2b)
Solution:
-5a (7a – 2b) = -5a x 7a- 5a x (-2b)
= -35a² + 10ab

Question 4.
-11y² (3y + 7)
Solution:
-11y² (3y + 7) = -11y² x 3y – 11y² x 7
= -33y²⁺¹-77y²
= 33y³-77y²

Question 5.
\(\frac { 6x }{ 5 }\) (x³+y³)
Solution:

Question 6.
xy (x³-y³)
Solution:
xy (x³ – y³) =xy x x³ – xy x y³
= x^{1 + 3} x y – x x y¹⁺³
= x⁴y – xy⁴

Question 7.
0.1y (0.1x⁵ + 0.1y)
Solution:
0.1y (0.1x⁵ + 0.1y) = 0.1y x 0.1x⁵ + 0.1y x 0.1y
= 0.01x⁵y + 0.01y²

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.
5x (10x²y – 100xy²)
Solution:
5x (10x²y – 100xy²)
= 1.5x x 10x²y – 1.5x x 100xy²
= 15x^{1 + 2}y- 150x¹⁺¹ x y²
15 x³y- 150x² y²

Question 12.
4.1xy (1.1x-y)
Solution:
4.1xy (1.1x-y) = 4.1xy x 1.1x – 4.1xy x y
= 4.51x²y-4.1xy²

Question 13.

Solution:

Question 14.

Solution:

Question 15.
\(\frac { 4 }{ 3 }\) a (a² + 6² – 3c²)
Solution:

Question 16.
Find the product 24x² (1 – 2x) and evaluate its value for x = 3.
Solution:
24x² (1 – 2x) = 24x² x 1 + 24x² x (-2x)
= 24x² + (-48x²⁺¹)
= 24x² – 48x³
If x = 3, then
= 24 (3)² – 48 (3)³
= 24 x 9-48 x 27 = 216- 1296
= -1080

Question 17.
Find the product of -3y (xy +y²) and find its value for x = 4, and y = 5.
Solution:
-3y (xy + y²) = -3y x xy – 3y x y²
= -3xy² -3y^{2 +1}  = -3xy² – 3y³
If x = 4, y = 5, then
= -3 x 4 (5)² – 3 (5)³ = -12 x 25 – 3 x 125
= -300 – 375 = – 675

Question 18.
Multiply – \(\frac { 3 }{ 2 }\) x²y³ by (2x-y) and verify the answer for x = 1 and y = 2.
Solution:

Question 19.
Multiply the monomial by the binomial and find the value of each for x = -1, y = 25 and z =05 :
(i) 15y² (2 – 3x)
(ii) -3x (y² + z²)
(iii) z² (x – y)
(iv) xz (x² + y²)
Solution:

Question 20.
Simplify :
(i) 2x² (at¹ – x) – 3x (x⁴ + 2x) -2 (x⁴ – 3x²)
(ii) x³y (x² – 2x) + 2xy (x³ – x⁴)
(iii) 3a² + 2 (a + 2) – 3a (2a + 1)
(iv) x (x + 4) + 3x (2x² – 1) + 4x² + 4
(v) a (b-c) – b (c – a) – c (a – b)
(vi) a (b – c) + b (c – a) + c (a – b)
(vii) 4ab (a – b) – 6a² (b – b²) -3b² (2a² – a) + 2ab (b-a)
(viii) x² (x² + 1) – x³ (x + 1) – x (x³ – x)
(ix) 2a² + 3a (1 – 2a³) + a (a + 1)
(x) a² (2a – 1) + 3a + a³ – 8
(xi) \(\frac { 3 }{ 2 }\)-x² (x² – 1) + \(\frac { 1 }{4 }\)-x² (x² + x) – \(\frac { 3 }{ 4 }\)x (x³ – 1)
(xii) a²b (a – b²) + ab² (4ab – 2a²) – a³b (1 – 2b)
(xiii )a²b (a³ – a + 1) – ab (a⁴ – 2a² + 2a) – b (a³– a² -1)
Solution:
(i) 2x² (x³ -x) – 3x (x⁴ + 2x) -2 (x⁴ – 3x²)
= 2x² x x³-2x²x x-3x x x⁴-3x x 2x-2x⁴ + 6x²
= 2x^{2 + 3}– 2x^{2 +1} – 3x^{,1+ 4}-6x^,1+1 -2x⁴ + 6x²
= 2x⁵ – 2x³ – 3x⁵ — 6x² – 2x⁴ + 6x²
= 2x⁵ – 3x⁵ – 2a⁴ – 2x³ + 6x² – 6x²
= -x⁵ – 2x⁴ – 2x³ + 0
= -x⁵-2x⁴-2x³
(ii) x³y (x² – 2x) + 2xy (x³ – x⁴)
= x³y x x² – x³y x 2x + 2ay x ac³ – 2xy x x⁴
= x^{3 + 2}y-2x^{3 + 1} y + 2x^{1 + 3}y – 2yx⁴⁺¹
= x⁵y – 2x⁴y + 2x⁴y – 2yx⁵
= -x⁵y
(iii) 3a² + 2 (a + 2) – 3a (2a + 1)
= 3a² + 2a + 4 – 6a² – 3a
= 3a² – 6a² + 2a – 3a + 4
= -3a² – a + 4
(iv) x (x + 4) + 3x (2x² – 1) + 4x² + 4
= x² + 4x + 3x x 2x² – 3x x 1 + 4x² + 4
= x² + 4x + 6x^{2 +1} – 3x + 4x² + 4
= x² + 4x + 6x³ – 3x + 4x² + 4
= 6a³ + 4x² + x² + 4x – 3x + 4
= 6x³ + 5x² + x + 4
(v) a (b – c)-b (c – a) – c (a – b)
= ab – ac – be + ab – ac + bc
= 2ab – 2ac
(vi) a (b – c) + b (c – a) + c (a – b)
= ab – ac + bc – ab + ac – bc
= ab – ab + bc – be + ac – ac
= 0
(vii) 4ab (a – b) – 6a² (b – b²) -3b² (2a² – a) + 2ab (b – a)
= 4a²b – 4ab² – 6a²b + 6a²b² – 6a²b² + 3ab² + 2ab² – 2a²b
= 4a²b- 6a²b – 2 a²b – 4ab² + 3 ab² + 2ab² + 6a²b² – 6a²b²
= 4a²b – 8a²b – 4ab² + 5 ab² + 0
= – 4a²b + ab²
(viii) x² (x² + 1) – x³ (x + 1) – x (x³ – x)
= x^{2 + 2} + x² – x^{3 + 1} – x³ – x^{1 + 3} + x^{1 + 1}
= x⁴ + x²-x⁴-x³-x⁴ + x²
= x⁴-x⁴-x⁴-x³ + x² + x²
= -x⁴ – x³ + 2x²
(ix) 2a² + 3a (1 – 2a³) + a (a + 1)
= 2a² + 3 a – 3 a x 2a³ + a² + a
= 2a² + 3a – 6a^{1 + 3} + a² + a
= 2a² + 3a – 6a⁴ + a² + a
= -6a⁴ + 3a² + 4a
(x) a² (2a – 1) + 3a + a³ – 8
= 2 a² x a – a² x 1+3a + a³-8
= 2a³ – a² + 3a + a³ – 8
= 2a³ + a³ – a² + 3a – 8
= 3a³ – a² + 3a – 8

(xii) a²b (a – b²) + ab² (4ab – 2a²) – a³b (1 – 2b)
= a²b x a – a²b x b¹ + ab² x 4ab – ab¹ x2a² -a³b x 1 + a³b x 2b
= a²⁺¹ b-a²b^{2 +1}+ 4a^{1 +1} b^{2 +1} -2a²⁺¹ b²-a³b + 2a³b^{1 +1}
= a’b – a²b³ + 4a²b³ – 2a³b² – a³b + 2a³b²
= a³b – a³b – a²b³ + 4a²b³ – 2a³b² + 2a³b²
= 0 + 3a²b³ + 0 = 3 a²b³
(xiii) a²b (a³ – a + 1) – ab (a⁴ – 2a² + 2a) – b (a³ -a²– 1)
= a²b x _a³ – a²b x _a + a²b – ab x a² + ab x 2a² – ab x 2a- ba³ + ba² + b
= a^2+ 3b – a²⁺¹ b + a²b -a^{1 + 4}b + 2a^{1 + 2}b- 2a¹⁺¹ b- a³b + a²b + b
= a⁵b – a³b + a²6 – a⁵b + 2a³b – 2a²b – a³b + a²b + b
= a⁵b – a³b + 2a³b – a³6 – a³b + a²b – 2a²b + a²b + b
= a³b – a⁵b + 2a³b – 2a³b + 2a²b-2a²b + b
= 0 + 0 + 0 + b = b

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 20 Mensuration I (Area of a Trapezium and a Polygon) Ex 20.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3

Question 1.
Find the area, in square metres, of the trapezium whose bases and altitude are as under:
(i) bases = 12 dm and 20 dm, altitude =10 dm
(ii) bases = 28 cm and 3 dm, altitude = 25 cm
(iii) bases = 8 m and 60 dm, altitude = 40 dm
(iv) bases = 150 cm and 30 dm, altitude = 9 dm
Solution:

Question 2.
Find the area of trapezium with base 15 cm and height 8 cm. If the side parallel to the given base is 9 cm long.
Solution:
In the trapezium ABCD,

Question 3.
Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
Solution:
Length of parallel sides of a trapezium are 16 dm and 22 dm i.e.
b₁ = 16 dm, b₂ = 22 dm
and height (h) = 12 dm

Question 4.
Find the height of a trapezium, the sum of lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm²
Solution:
Sum of parallel sides (b₁ + b₂) = 60 cm
Area of trapezium = 600 cm²

Question 5.
Find the altitude of a trapezium whose area is 65 cm² and whose bases are 13 cm and 26 cm.
Solution:
Area of a trapezium = 65 cm²
Bases are 13 cm and 26 cm
i.e. b₁ = 13 cm, b₂ = 26 cm.

Question 6.
Find the sum of the lengths of the bases of trapezium whose area is 4.2 m² and whose height is 280 cm.
Solution:
Area of trapezium = 4.2 m²
Height (h) = 280 cm = 2.8 m.

Question 7.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate the area as
(i) the sum of the areas of two triangles and one rectangle.
(ii) the difference of the area of a rectangle id the sum of the areas of two triangles.
Solution:
In trapezium ABCD, parallel sides or bases are 10 cm and 15 cm and height = 6 cm
Area of trapezium


Area of trapezium = 90 – 15 = 75 cm²
= area of rectangle – areas of two triangles.

Question 8.
The area of a trapezium is 960 cm². If the parallel sides are 34 cm and 46 cm, find the distance between them:
Solution:
Area of trapezium = 960 cm²
Parallel sides are 34 cm and 46 cm
b₁ + b₂ = 34 + 46 = 80 cm

Distance between parallel sides = 24 cm

Question 9.
Find the area of the figure as the sum of the areas of two trapezium and a rectangle.

Solution:
In the figure,
One rectangle is ABCD whose sides are 50 cm and 10 cm.
Two trapezium of equal size in which parallel sides are 30 cm and 10 cm and height

Question 10.
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.

Solution:
Top of a table is of trapezium in shape whose parallel sides are 1 m and 1.2 m and distance between them (h) = 0.8 m
Area of trapezium = \(\frac { 1 }{ 2 }\) (Sum of parallel sides) x height

Question 11.
The cross-section of a canal is a trapezium in shape. If the canal is 10 m wide at the top 6 m wide at the bottom, and the area of the cross-section is 72 m², determine its depth.
Solution:
Area of cross-section = 72 m²
Parallel sides of the trapezium = 10 m and 6 m

Question 12.
The area of a trapezium is 91 cm² and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
Solution:
Area of trapezium = 91 cm²
Height (h) = 7 cm.
Sum of parallel sides

One parallel side = 9 cm
and second side = 9 + 8 = 17 cm
Hence parallel sides are 17 cm, 9 cm

Question 13.
The area of a trapezium is 384 cm². Its parallel sides are in the ratio 3 : 5 and the perpendicular distance between them is 12 cm. Find the length of each one of the parallel sides.
Solution:
Area of trapezium = 384 cm²
Perpendicular distance (h) = 12 cm
Sum of parallel sides

First parallel side = 8 x 3 = 24 cm
Second side = 8 x 5 = 40 cm

Question 14.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel and twice the side along the road. If the area of this field is 10500 m² and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.

Solution:
Area of the trapezium shaped field = 10500 m²
and perpendicular distance between them (h) = 100 m.

Question 15.
The area of trapezium is 1586 cm² and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
Solution:
Area of a trapezium = 1586 cm²
and distance between the parallel sides (h) = 26

Question 16.
The parallel sides of a trapezium are 25 cm and 13 cm ; Its nonparallel sides are equal each being 10 cm, find the area of the trapezium.
Solution:
Parallel sides of a trapezium ABCD are 25 cm and 13 cm
i.e. AB = 25 cm, CD = 13 cm
and each non-parallel side = 10 cm
i.e., AD = BC = 10 cm
From C, draw CE || DA and draw CL ⊥ AB
CE = DA = CB = 10 cm
and EB = AB – AE = AB – DC = 25 – 13 = 12 cm
Perpendicular CL bisects base EB of an isosceles ∆CED

Question 17.
Find the area of a trapezium whose parallel sides are 25 cm, 13 cm and other sides are 15 cm each.
Solution:
In trapezium ABCD, parallel sides are AB and DC.

AB = 25 cm, CD = 13 cm
and other sides are 15 cm each i.e. AD = CB = 15 cm
From C, draw CE || DA and CL ⊥ AB
AE = DC = 13 cm
and EB = AB – AE = 25 – 13 = 12 cm
Perpendicular CL bisects the base EB of the isosceles triangle CEB

Question 18.
If the area of a trapezium is 28 cm² and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
Solution:
Area of trapezium = 28 cm²
Altitude (h) = 4 cm.

One of the parallel side = 6 cm
Second parallel side = 14 – 6 = 8 cm

Question 19.
In the figure, a parallelogram is drawn in a trapezium the area of the parallelogram is 80 cm², find the area of the trapezium.

Solution:
Area of parallelogram (AECD) = 80 cm²
Side AE (b) = 10 cm

Question 20.
Find the area of the field shown in the figure by dividing it into a square rectangle and a trapezium.

Solution:
Produce EF to H to meet AB at H and draw DK || EH
HF = 4 cm, KD = HE = 4 + 4 = 8 cm
HK = ED = 4 cm,
KB = 12 – (8) = 4 cm
Now, area of square AGFH = 4 x 4 = 16 cm²
area of rectangle KDEH = l x b = 8 x 4 = 32 cm²
and area of trapezium BCDK.

Total area of the figure = 16 + 32 + 22 = 70 cm²

Hope given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.