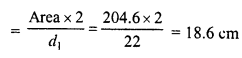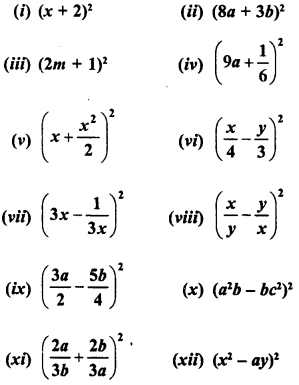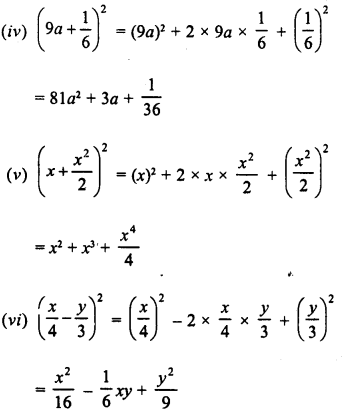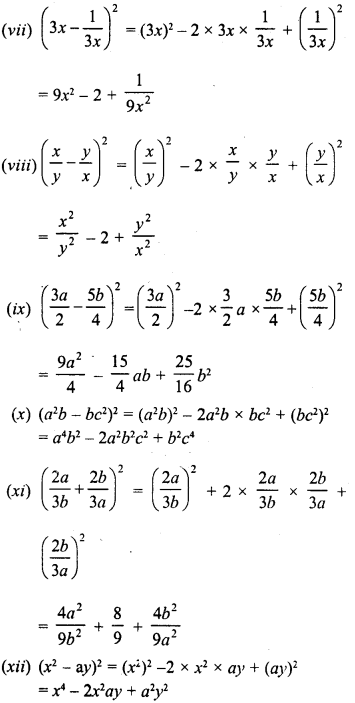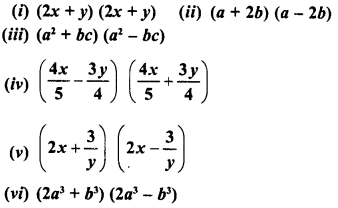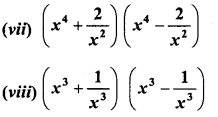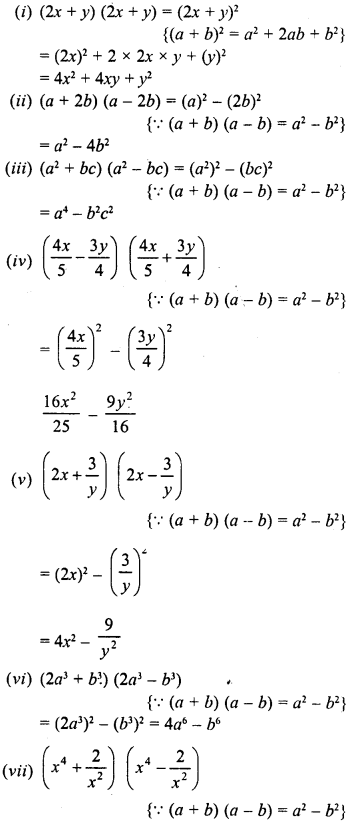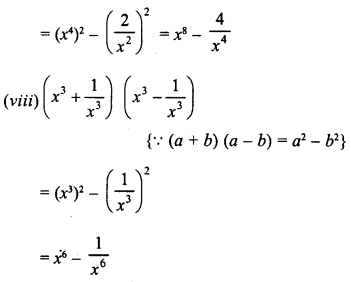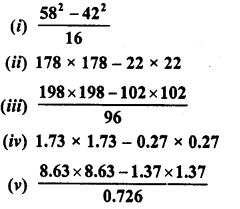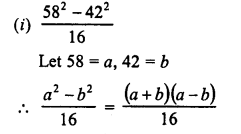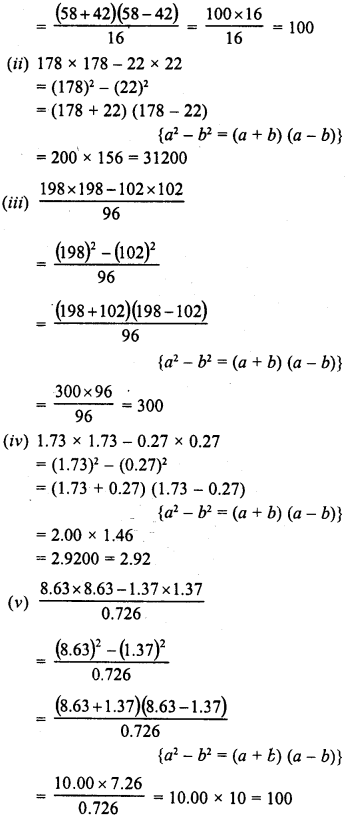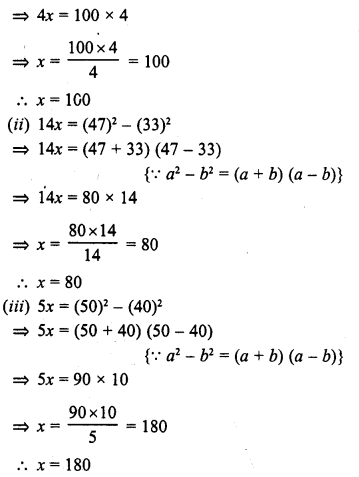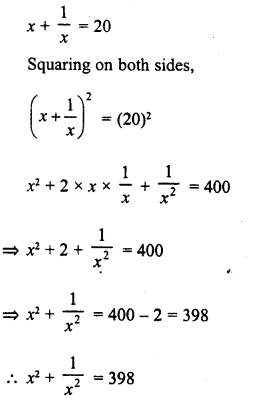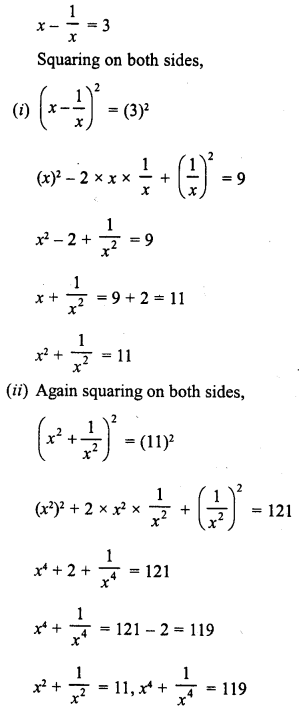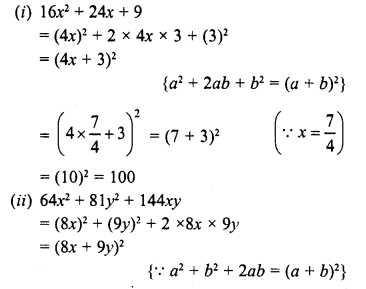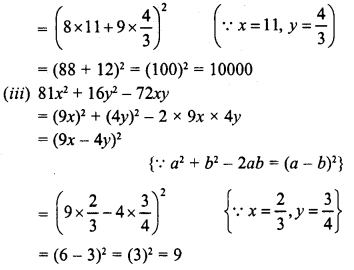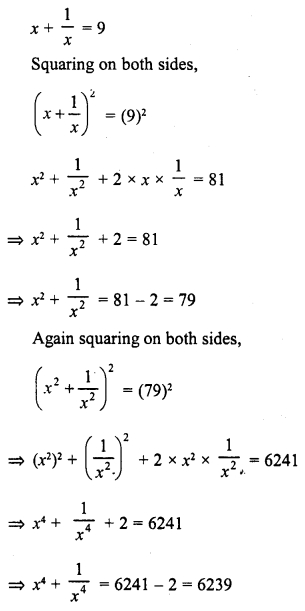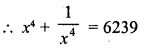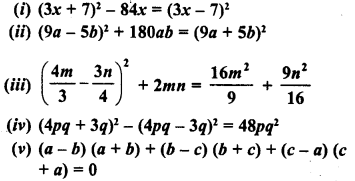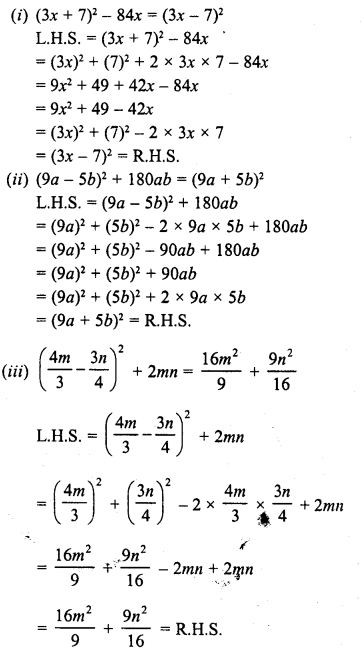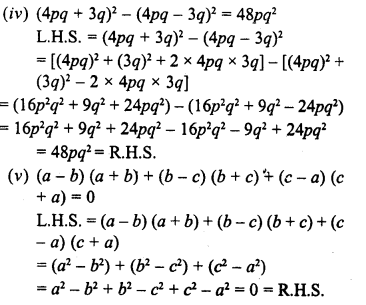Category: CBSE Class 8

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Question 1.
Find the following products :

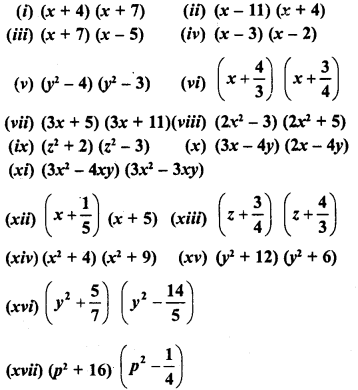
Solution:

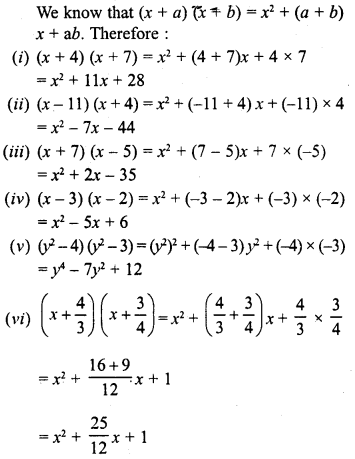
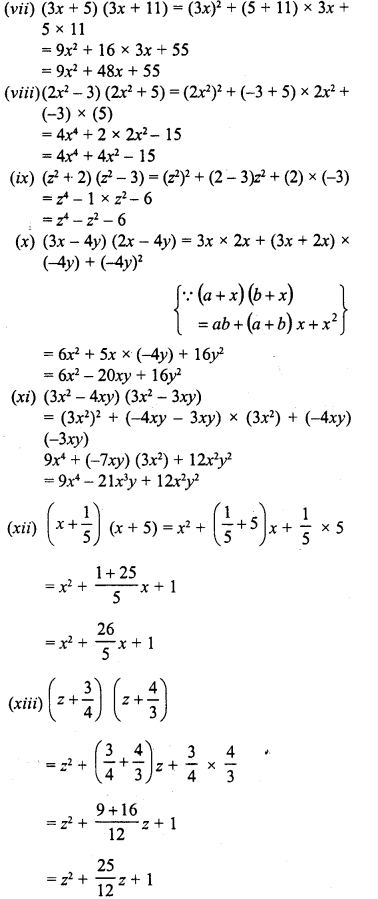
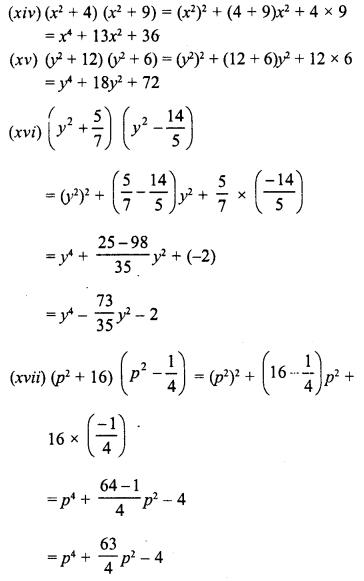
Question 2.
Evaluate the following :
(i) 102 x 106
(ii) 109 x 107
(iii) 35 x 37
(iv) 53 x 55
(v) 103 x 96
(vi) 34 x 36
(vii) 994 x 1006
Solution:
(i) 102 x 106 = (100 + 2) (100 + 6)
= (100)² + (2 + 6) x 100 + 2 x 6
= 10000 + 800 + 12 = 10812

(ii) 109 x 107 = (100 + 9) (100 + 7)
= (100)² + (9 + 7) x 100 + 9 x 7
=10000 + 1600 + 63 = 11663

(iii) 35 x 37 = (30 + 5) (30 + 7)
= (30)² + (5 + 7) x 30 + 5 x 7
= 900 + 12 x 30 + 35
= 900 + 360 + 35 = 1295

(iv) 53 x 55 = (50 + 3) (50 + 5)
= (50)² + (3 + 5) x 50 + 3 x 5
= 2500 + 8 x 50 + 15
= 2500 + 400+ 15 = 2915

(v)103 x 96 = (100 + 3) (100-4)
= (100)² + (3 – 4) x 100 + 3 x (-4)
= 10000+ (-1) x 100-12
= 10000 – 100 – 12 = 10000 – 112 = 9888

(vi) 34 x 36 = (30 + 4) (30 + 6)
= (30)² + (4 + 6) x 30 + 4 x 6
= 900 + 10 x 30 + 24
= 900 + 300 + 24 = 1224

(vii) 994 x 1006 = (1000 – 6) (1000 + 6)
= (1000)² + (-6 + 6) x 1000 + (-6) x 6
= 1000000 + 0-36
= 1000000-36 = 999964

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 16 Understanding Shapes II (Quadrilaterals) Ex 16.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 16 Understanding Shapes II Ex 16.1

Question 1.
Define the following terms:
(i) Quadrilateral
(ii) Convex Quadrilateral.
Solution:
(i) Quadrilateral: A closed figure made of four line segments is called a quadrilateral such that:

(a) no three points of them are collinear
(b) the line segments do not intersect except at their ends points.
(ii) Convex quadrilateral: A quadrilateral is called a convex quadrilateral of the line containing any side of the quadrilateral has the remaining vertices on the same side of it. In the figure, quadrilateral ABCD is a convex quadrilateral.

Question 2.
In a quadrilateral, define each of the following:
(i) Sides
(ii) Vertices
(iii) Angles
(iv) Diagonals
(v) Adjacent angles
(vi) Adjacent sides
(vii) Opposite sides
(viii) Opposite angles
(ix) Interior
(x) Exterior
Solution:
(i) Sides: In a quadrilateral ABCD, form line segments AB, BC, CD and DA are called sides of the quadrilateral.
(ii) Vertices : The ends points are called the vertices of the quadrilateral. Here in the figure, A, B, C and D are its vertices.
(iii) Angles: A quadrilateral has four angles which are at their vertices. In the figure, ∠A, ∠B, ∠C and ∠D are its angles.
(iv) Diagonals: The line segment joining the opposite vertices is called diagonal. A quadrilateral has two diagonals.
(v) Adjacent Angles : The angles having a common arm (side) are called adjacent angles.
(vi) Adjacent sides : If two sides of a quadrilateral have a common end-point, these are called adjacent sides.
(vii) Opposite sides: If two sides do not have a common end-point of a quadrilateral, they are called opposite sides.
(viii) Opposite angles : The angles which are not adjacent are called opposite angles.
(ix) Interior: The region which is surrounded by the sides of the quadrilateral is called its interior.
(x) Exterior : The part of the plane made up by all points as the not enclosed by the quadrilateral, is called its exterior.

Question 3.
Complete each of the following, so as to make a true statement:
(i) A quadrilateral has ………… sides.
(ii) A quadrilateral has ………… angles.
(iii) A quadrilateral has ……….. vertices, no three of which are …………
(iv) A quadrilateral has …………. diagonals.
(v) The number of pairs of adjacent angles of a quadrilateral is ………….
(vi) The number of pairs of opposite angles of a quadrilateral is ……………
(vii) The sum of the angles of a quadrilateral is …………
(viii) A diagonal of a quadrilateral is a line segment that joins two ………. vertices of the quadrilateral.
(ix) The sum of the angles of a quadrilateral is …………. right angles.
(x) The measure of each angle of a convex quadrilateral is …………. 180°.
(xi) In a quadrilateral the point of intersection of the diagonals lies in ………….. of the quadrilateral.
(xii) A point is in the interior of a convex quadrilateral, if it is in the ……….. of its two opposite angles.
(xiii) A quadrilateral is convex if for each side, the remaining …………. lie on the same side of the line containing the side.
Solution:
(i) A quadrilateral has four sides.
(a) A quadrilateral has four angles.
(iii) A quadrilateral has four vertices, no three of which are collinear .
(iv) A quadrilateral has two diagonals.
(v) The number of pairs of adjacent angles of a quadrilateral is four .
(vi) The number of pairs of opposite angles ot a quadrilateral is two.
(vii) The sum of the angles of a quadrilateral is 360°.
(viii) A diagonal of a quadrilateral is a line segment that join two opposite vertices of the quadrilateral.
(ix) The sum of the angles of a quadrilateral is 4 right angles.
(x) The measure of each angle of a convex quadrilateral is less than 180°.
(xi) In a quadrilateral the point of intersection of the diagonals lies in interior of the quadrilateral.
(xii) A point is in the interior of a convex quadrilateral, if it is in the interior of its two opposite angles.
(xiii) A quadrilateral is convex if for each side, the remaining vertices lie on the same side of the line containing the side.

Question 4.
In the figure, ABCD is a quadrilateral.
(i) Name a pair of adjacent sides.
(ii) Name a pair of opposite sides.
(iii) How many pairs of adjacent sides are there?
(iv) How many pairs of Opposite sides are there ?

(v) Name a pair of adjacent angles.
(vi) Name a pair of opposite angles.
(vii) How many pairs of adjacent angles are there ?
(viii) How many pairs of opposite angles are there ?
Solution:
In the figure, ABCD is a quadrilateral
(i) Pairs of adjacent sides are AB, BC, BC, CD, CD, DA, DA, AB.
(ii) Pairs of opposite sides are AB and CD; BC and AD.
(iii) There are four pairs of adjacent sides.
(iv) There are two pairs of opposite sides.
(v) Pairs of adjacent angles are ∠A, ∠B; ∠B, ∠C; ∠C, ∠D; ∠D, ∠A.
(vi) Pairs of opposite angles are ∠A and ∠C; ∠B and ∠D.
(vii) There are four pairs of adjacent angles.
(viii) There are two pairs of opposite angles.

Question 5.
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
Solution:
Sum of four angles of quadrilateral is 360°
110° + 12° + 55° + x° = 360°
⇒ 237° + x° = 360°
⇒ x° = 360° – 237° = 123°
x = 123°

Question 6.
The three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
Solution:
The sum of four angles of a quadrilateral = 360°
Three angles are 110°, 50° and 40°
Let fourth angle = x
Then 110° + 50° + 40° + x° = 360°
⇒ 200° + x° = 360°
⇒ x = 360° – 200° = 160°
x = 160°

Question 7.
A quadrilateral has three acute angles each measures 80°. What is the measure of fourth angle ?
Solution:
Sum of four angles of a quadrilateral = 360°
Sum of three angles having each angle equal to 80° = 80° x 3 = 240°
Let fourth angle = x
Then 240° + x = 360°
⇒ x° = 360° – 240°
⇒ x° = 120°
Fourth angle = 120°

Question 8.
A quadrilateral has all its four angles of the same measure. What is the measure of each ?
Solution:
Let each equal angle of a quadrilateral = x
4x° = 360°
⇒ x° = \(\frac { 360 }{ 4 }\) = 90°
Each angle will be = 90°

Question 9.
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles ?
Solution:
Measures of two angles each = 65°
Sum of these two angles = 2 x 65°= 130°
But sum of four angles of a quadrilateral = 360°
Sum of the remaining two angles = 360° – 130° = 230°
But these are equal to each other
Measure of each angle = \(\frac { 230 }{ 2 }\) = 115°

Question 10.
Three angles of a quadrilateral are equal. Fourth angle is of measure 150°. What is the measure of equal angles ?
Solution:
Sum of four angles of a quadrilateral = 360°
One angle = 150°
Sum of remaining three angles = 360° – 150° = 210°
But these three angles are equal
Measure of each angle = \(\frac { 210 }{ 3 }\) = 70°

Question 11.
The four angles of a quadrilateral are as 3 : 5 : 7 : 9. Find the angles.
Solution:
Sum of four angles of a quadrilateral = 360°
and ratio in angles = 3 : 5 : 7 : 9
Let first angles = 2x
Then second angle = 5x
third angle = 7x
and fourth angle = 9x
3x + 5x + 7x + 9x = 360°
⇒ 24x = 369°
⇒ x = \(\frac { 360 }{ 24 }\) = 15°
First angle = 3x = 3 x 15° = 45°
second angle = 5x = 5 x 15° = 75°
third angle = 7x = 7 x 15° = 105°
and fourth angle = 9x = 9 x 15° = 135°

Question 12.
If the sum of the two angles of a quadrilateral is 180°, what is the sum of the remaining two angles ?
Solution:
Sum of four angles of a quadrilateral = 360°
and sum of two angle out of these = 180°
Sum of other two angles will be = 360° – 180° = 180°

Question 13.
In the figure, find the measure of ∠MPN.

Solution:
In the figure, OMPN is a quadrilateral in which
∠O = 45°, ∠M = ∠N = 90° (PM ⊥ OA and PN ⊥ OB)
Let ∠MPN = x°
∠O + ∠M + ∠N + ∠MPN = 360° (Sum of angles of a quadrilateral)
⇒ 45° + 90° + 90° + x° = 360°
⇒ 225° + x° = 360°
⇒ x° = 360° – 225°
⇒x = 135°
∠MPN = 135°

Question 14.
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles ?
Solution:
The sides of a quadrilateral ABCD are produced in order, forming exterior angles ∠1, ∠2, ∠3 and ∠4.

Now ∠DAB + ∠1 = 180° (Linear pair) ……(i)
Similarly,
∠ABC + ∠2 = 180°
∠BCD + ∠3 = 180°
and ∠CDA + ∠4 = 180°
Adding, we get
∠DAB + ∠1 + ∠ABC + ∠2 + ∠BCD + ∠3 + ∠CDA + ∠4 = 180° + 180° + 180° + 180° = 720°
⇒ ∠DAB + ∠ABC + ∠CDA + ∠ADC + ∠1 + ∠2 + ∠3 + ∠4 = 720°
But ∠DAB + ∠ABC + ∠CDA + ∠ADB = 360° (Sum of angles of a quadrilateral)
360° + ∠1 + ∠2 + ∠3 + ∠4 = 720°
⇒ ∠l + ∠2 + ∠3 + ∠4 = 720° – 360° = 360°
Sum of exterior angles = 360°

Question 15.
In the figure, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
Solution:
In quadrilateral ABCD,

∠D = 50°, ∠C = 100°
PA and PB are the bisectors of ∠A and ∠B.
In quadrilateral ABCD,
∠A + ∠B + ∠C + ∠D = 360° (Sum of angles of a quadrilateral)
⇒ ∠A + ∠B + 100° + 50° = 360°
⇒ ∠A + ∠B + 150° = 360°’
⇒ ∠A + ∠B = 360° – 150° = 210°
and \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B = \(\frac { 210 }{ 2 }\) = 105°
(PA and PB are bisector of ∠A and ∠B respectively)
∠PAB + ∠PBA = 105°
⇒ ∠PAB + ∠PBA + ∠APB = 180° (Sum of angles of a triangle)
⇒ 105° + ∠APB = 180°
⇒ ∠APB = 180° – 105° = 75°
∠APB = 75°

Question 16.
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angle of the quadrilateral.
Solution:
Sum of angles A, B, C and D of a quadrilateral = 360°
i.e. ∠A + ∠B + ∠C + ∠D = 360°
But ∠A = ∠B = ∠C = ∠D = 1 : 2 : 4 : 5

Let ∠A = x,
Then ∠B = 2x
∠C = 4x
∠D = 5x
x + 2x + 4x + 5x = 360°
⇒ 12x = 360°
⇒ x = \(\frac { 360 }{ 12 }\) = 30°
∠A = x = 30°
∠B = 2x = 2 x 30° = 60°
∠C = 4x = 4 x 30° = 120°
∠D = 5A = 5 x 30° = 150°

Question 17.
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD = \(\frac { 1 }{ 2 }\) (∠A + ∠B).
Solution:
In quadrilateral ABCD,

Question 18.
Find the number of sides of a regular polygon when each of its angles has a measures of
(i) 160°
(ii) 135°
(iii) 175°
(iv) 162°
(v) 150°.
Solution:
In a n-sided regular polygon, each angle

Question 19.
Find the number of degrees in each exterior angle of a regular pentagon.
Solution:
In a pentagon or a polygon, sum of exterior angles formed by producing the sides in order, is four right angles or 360°
Each exterior angle = \(\frac { 360 }{ 5 }\) = 72°

Question 20.
The measure of angles of a hexagon are x°, (x – 5)° (x – 5)°, (2x – 5)°, (2x – 5)°, (2x + 20)°. Find the value of x.
Solution:
We know that the sum of interior angels of a hexagon = 720° (180° x 4)
⇒ x + x – 5 + x – 5 + 2x – 5 + 2x – 5 + 2x + 20 = 720°
⇒ 9x – 20 + 20 = 720
⇒ 9x = 720
⇒ x = \(\frac { 720 }{ 9 }\) = 80°
x = 80°

Question 21.
In a convex hexagon, prove that the sum of all interior angles is equal to twice the sum of its exterior angles formed by producing the sides in the same order.
Solution:
In a convex hexagon ABCDEF, its sides AB, BG, CD, DE, EF and FA are produced in order forming exterior angles a, b, c, d, e, f

∠a + ∠b + ∠c + ∠d + ∠e + ∠f = 4 right angles (By definition)
By joining AC, AD, and AE, 4 triangles ABC, ACD, ADE and AEF are formed
In ∆ABC,
∠1 + ∠2 + ∠3 = 180° = 2 right angle (Sum of angles of a triangle) …… (i)
Similarly,
In ∆ACD,
∠4 +∠5 + ∠6 = 180° = 2 right angles
In ∆ADE,
∠1 + ∠8 + ∠9 = 2 right angles …(iii)
In ∆AEF,
∠10 + ∠11 + ∠12 = 2 right angles …(iv)
Joining (i), (ii), (iii) and (iv)
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 + ∠9 + ∠10 + ∠11 + ∠12 = 8 right angles
⇒ ∠2 + ∠3 + ∠5 + ∠6 + ∠8 + ∠9 + ∠11 + ∠12 + ∠1 + ∠4 + ∠7 + ∠10 = 8 right angles
⇒ ∠B + ∠C + ∠D + ∠E +∠F + ∠A = 8 right angles
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 2 (∠a + ∠b + ∠c + ∠d + ∠e + ∠f)
Sum of all interior angles = 2(the sum of exterior angles)
Hence proved.

Question 22.
The sum of the interior angles of a polygon is three times the sum of its exterior angles. Determine the number of sides of the polygon.
Solution:
Let number of sides of a regular polygon = n
Each interior angle = \(\frac { 2n – 4 }{ n }\) right angles
Sum of all interior angles = \(\frac { 2n – 4 }{ n }\) x n
right angles = (2n – 4) right angles
But sum of exterior angles = 4 right angles
According to the condition,
(2n – 4) = 3 x 4 (in right angles)
⇒ 2n – 4 = 12
⇒ 2n = 12 + 4 = 16
⇒ n = 8
Number of sides of the polygon = 8

Question 23.
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
Solution:
Ratio in exterior angle and interior angles of a regular polygon = 1 : 5
But sum of interior and exterior angles = 180° (Linear pair)

By cross multiplication:
6n – 12 = 5n
⇒ 6n – 5n = 12
⇒ n = 12
Number of sides of polygon is 12

Question 24.
PQRSTU is a regular hexagon. Determine each angle of ∆PQT.
Solution:
In regular hexagon, PQRSTU, diagonals PT and QT are joined.

In ∆PUT, PU = UT
∠UPT = ∠UTP
But ∠UPT + ∠UTP = 180° – ∠U = 180° – 120° = 60°
∠UPT = ∠UTP = 30°
∠TPQ = 120° – 30° = 90° (QT is diagonal which bisect ∠Q and ∠T)
∠PQT = \(\frac { 120 }{ 2 }\) = 60°
Now in ∆PQT,
∠TPQ + ∠PQT + ∠PTQ = 180° (Sum of angles of a triangle)
⇒ 90° + 60° + ∠PTQ = 180°
⇒ 150° + ∠PTQ = 180°
⇒ ∠PTQ = 180° – 150° = 30°
Hence in ∆PQT,
∠P = 90°, ∠Q = 60° and ∠T = 30°

Hope given RD Sharma Class 8 Solutions Chapter 16 Understanding Shapes II Ex 16.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I (Polygons) Ex 15.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I Ex 15.1

Question 1.
Draw rough diagrams to illustrate the following:
(i) Open curve
(ii) Closed curve
Solution:

Question 2.
Classify the following curves as open or closed.

Solution:
Open curves : (i), (iv) and (v) are open curves.
(ii) , (iii), and (vi) are closed curves.

Question 3.
Draw a polygon and shade its interior. Also draw its diagonals, if any.
Solution:
In the given polygon, the shaded portion is its interior region AC and BD are the diagonals of polygon ABCD.

Question 4.
Illustrate, if possible, each one of the following with a rough diagram:
(i) A closed curve that is not a polygon.
(ii) An open curve made up entirely of line segments.
(iii) A polygon with two sides.
Solution:
(i) Close curve but not a polygon.

(ii) An open curve made up entirely of line segments.

(iii) A polygon with two sides. It is not possible. At least three sides are necessary

Question 5.
Following are some figures : Classify each of these figures on the basis of the following:


(i) Simple curve
(ii) Simple closed curve
(iii) Polygon
(iv) Convex polygon
(v) Concave polygon
(vi) Not a curve
Solution:
(i) It is a simple closed curve and a concave polygon.
(ii) It is a simple closed curve and convex polygon.
(iii) It is neither a curve nor polygon.
(iv) it is neither a curve not a polygon.
(v) It is a simple closed curve but not a polygon.
(vi) It is a simple closed curve but not a polygon.
(vii) It is a simple closed curve but not a polygon.
(viii) It is a simple closed curve but not a polygon.

Question 6.
How many diagonals does each of the following have ?
(i) A convex quadrilateral
(ii) A regular hexagon
(iii) A triangle.
Solution:
(i) A convex quadrilateral
Here n = 4

Question 7.
What is a regular polygon ? State the name of a regular polygon of:
(i) 3 sides
(ii) 4 sides
(iii) 6 sides.
Solution:
A regular polygon is a polygon which has all its sides equal and so all angles are equal,
(i) 3 sides : It is an equilateral triangle.
(ii) 4 sides : It is a square.
(iii) 6 sides : It is a hexagon.

Hope given RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I Ex 15.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 20 Mensuration I (Area of a Trapezium and a Polygon) Ex 20.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2
• RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3

Question 1.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m² ?
Solution:
Area of floor = 1080 m²
Base of parallelogram shaped tile (b) = 24 cm
and corresponding height (h) = 10 cm
Area of one tile = b x h = 24 x 10 = 240 cm²

Question 2.
A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Fig. If AB = 60 m and BC = 28 m, find the area of the plot.

Solution:
Length of rectangular portion (l) = 60 m
and breadth (b) = 28 m
Area of the rectangular plot = l x b = 60 x 28 m² = 1680 m²
Radius of semicircular portion (r) = \(\frac { b }{ 2 }\) = \(\frac { 28 }{ 2 }\) = 14 m
Area = \(\frac { 1 }{ 2 }\) πr²
= \(\frac { 1 }{ 2 }\) x \(\frac { 22 }{ 7 }\) x 14 x 14 m²
= 308 m²
Total area of the plot = 1680 + 308 = 1988 m²

Question 3.
A playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π = \(\frac { 22 }{ 7 }\)).
Solution:
Length of rectangular portion (l) = 36 m
and breadth (b) = 24.5 m

= \(\frac { 22 }{ 7 }\) x 150.0625 m²
= 471.625 m²
Total area of the playground = 471.625 + 882 = 1353.625 m²

Question 4.
A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 have been cut. Find the area of the remaining part.
Solution:
Length of rectangular piece (l) = 20 m
breadth (b) = 15 m

Area of rectangular piece = l x b = 20 x 15 = 300 m²
Radius of each quadrant (r) = 3.5 m
Total area of 4 quadrants

Area of the remaining portion = 300 – 38.5 m² = 261.5 m²

Question 5.
The inside perimeter of a running track (shown in Fig.) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

Solution:
Inner perimeter = 400 m.
Length (l) = 90 m.
Perimeter of two semicircles = 400 – 2 x 90 = 400 – 180 = 220 m

Question 6.
Find the area of the Figure in square cm, correct to one place of decimal. (Take π = \(\frac { 22 }{ 7 }\))

Solution:
Length of square (a) = 10 cm.
Area = a² = (10)² = 100 cm²
Base of the right triangle AED = 8 cm
and height = 6 cm

Question 7.
The diameter of a wheel of a bus is 90 cm which makes 315 revolutions per minute. Determine its speed in kilometres per hour. (Take π = \(\frac { 22 }{ 7 }\))
Solution:
Diameter of the wheel (d) = 90 cm.

Question 8.
The area of a rhombus is 240 cm² and one of the diagonal is 16 cm. Find another diagonal.
Solution:
Area of rhombus = 240 cm²
Length of one diagonal (d₁) = 16 cm
Second diagonal (d₂)

Question 9.
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution:
In rhombus, diagonal (d₁) = 7.5 cm
and diagonal (d₂) = 12 cm

Question 10.
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Solution:
In quadrilateral shaped field ABCD,
diagonal AC = 24 m

and perpendicular BL = 13 m
and perpendicular DM on AC = 8 m
Area of the field ABED = \(\frac { 1 }{ 2 }\) x AC x (BL + DM)
= \(\frac { 1 }{ 2 }\) x 24 x (13 + 8) m²
= 12 x 21 = 252 m²

Question 11.
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Solution:
Side of rhombus (b) = 6 cm
Altitude (h) = 4 cm

Question 12.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is Rs 4.
Solution:
Number of rhombus shaped tiles = 300
Diagonals of each tile = 45 cm and 130 cm

Rate of polishing the tiles = Rs 4 per m²
Total cost = 202.5 x 4 = Rs 810

Question 13.
A rectangular grassy plot is 112 m long and 78 broad. It has a gravel path 2.5 m wide all around it on the side. Find the area of the path and the cost of constructing it at Rs 4.50 per square metre.
Solution:
Length of rectangular plot (l) = 112 m
and breadth (b) = 78 m
Width of path = 2.5 m

Inner length = 112 – 2 x 2.5 = 112 – 5 = 107 m
and inner breadth = 78 – 2 x 2.5 = 78 – 5 = 73 m
Area of path = outer area – inner area
= (112 x 78 – 107 x 73) m² = 8736 – 7811 = 925 m²
Rate of constructing = Rs 4.50 per m²
Total cost = 925 x Rs 4.50 = Rs 4162.50

Question 14.
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
Solution:
Side of rhombus = 20 cm.
One diagonal (d₁) = 24 cm

Diagonals of a rhombus bisect each other at right angle
AB = 20 cm
and OA = \(\frac { 1 }{ 2 }\) AC = \(\frac { 1 }{ 2 }\) x 24 cm = 12 cm
In right-angled ∆AOB,
AB² = AO² + BO² (Pythagoras theorem)
⇒ (20)² = (12)² + BO²
⇒ 400 = 144 + BO²
⇒ BO² = 400 – 144 = 256 = (16)²
⇒ BO = 16 cm
and diagonal BD = 2 x BO = 2 x 16 = 32 cm
Now area of rhombus ABCD

Question 15.
The length of a side of a square field is 4 m. What will be the altitude of the rhombus if the area of the rhombus is equal to the square field and one of its diagonal is L m ?
Solution:
Side of square = 4 m
Area of square = (a)² = 4 x 4 =16 m²

Diagonals of a rhombus bisect each other at right angles.
In right ∆AOB
AB² = QA² + BO² (Pythagoras theorem)
= (8)² + (1)² = 64 + 1 = 65
AB = √65 m.
Now, length of perpendicular AL (h)

Question 16.
Find the area of the field in the form of a rhombus, if the length of each side be 14 cm and the altitude be 16 cm.
Solution:
Length of each side of rhombus = 14 cm.
Length of altitude = 16 cm
Area = Base x altitude = 14 x 16 cm² = 224 cm²

Question 17.
The cost of fencing a square field at 60 paise per metre is Rs 1,200. Find the cost of reaping the field at the rate of 50 paise per 100 sq. metres.
Solution:
Cost of fencing the square field = Rs 1,200
Rate = 60 paise per m.

Question 18.
In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.
Solution:
Side of a square plot = 84 m
Area = (a)² = (84)² = 84 x 84 m² = 7056 m²
Area of rectangular field = 7056 m²
Length (l) = 144 m

Question 19.
The area of a rhombus is 84 m². If its perimeter is 40 m, then find its altitude.
Solution:
Area of rhombus = 84 m²
Perimeter = 40 m

Question 20.
A garden is in the form of a rhombus whose side is 30 metres and the corresponding altitude is 16 m. Find the cost of levelling the garden at the rate of Rs 2 per m².
Solution:
Side of rhombus garden (b) = 30 m.
Altitude (h) = 16 m
Area = Base x altitude = 30 x 16 = 480 m²
Rate of levelling the garden = Rs 2 per m²
Total cost = Rs 480 x 2 = Rs 960

Question 21.
A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus ?
Solution:
Length of side of rhombus (b) = 64 m
and altitude (h) = 16 m
Area = b x h = 64 x 16 m² = 1024 m²
Now area of square = 1024 m²
Side of the square = √Area = √1024 m = 32 m

Question 22.
The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are 24.8 cm and 16.5 cm respectively. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.
Solution:
Base of triangle (b) = 24.8 cm
and altitude (h) = 16.5 cm
Area of triangle = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x bh= \(\frac { 1 }{ 2 }\) x 24.8 x 16.5 cm² = 204.6 cm²
Area of rhombus = 204.6 cm²
Length of one diagonal (d₁ = 22 cm
Second diagonal (d₂)

 

Hope given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
Mr. Cherian purchased a boat for Rs 16,000. If the total cost of the boat is depreciating at the rate of 5% per annum, calculate its value after 2 years.
Solution:
Cost of boat = Rs 16,000
Rate of depreciating = 5% p.a.
Period = 2 years
Value of boat after 2 years

Question 2.
The value of a machine depreciates at the rate of 10% per annum. What will be its value 2 years hence, if the present value is Rs 1,0,000 ? Also, find the total depreciation during this period.
Solution:
Present value of machine = Rs 1,00,000
Rate of depreciation = 10% p.a.
Period (n) = 2 years
Value of machine after 2 years

Question 3.
Pritam bought a plot of land for Rs 6,40,000. Its value is increasing by 5% of its previous value after every six months. What will be the value of the plot after 2 years ?
Solution:
Present value of plot = Rs 6,40,000
Increase = 5% per half year
Period (n) = 2 years or 4 half years

Question 4.
Mohan purchased a house for Rs 30,000 and its value is depreciating at the rate of 25% per year. Find the value of the house after 3 years.
Solution:
Present value of the house (P) = Rs 30,000
Rate of depreciation = 25% p.a.
Period (n) = 3 years
Value of house after 3 years

Question 5.
The value of a machine depreciates at the rate of 10% per annum. It was purchased 3 years ago. If its present value is Rs 43,740, find its purchased price.
Solution:
Let the purchase price of machine = Rs P
Rate of depreciation = 10% p.a.
Period (n) = 3 years.
and present value = Rs 43,740

Question 6.
The value of a refrigerator which was purchased 2 years ago, depreciates at 12% per annum. If its present value is Rs 9,680, for how much was it purchased ?
Solution:
Let the refrigerator was purchased for = Rs P
Rate of depreciation (R) = 12% p.a.
Period (n) = 2 years
and present value (A) = Rs 9,680

Question 7.
The cost of a TV set was quoted Rs 17,000 at the beginning of 1999. In the beginning of2000, the price was hiked by 5%. Because of decrease in demand the cost was reduced by 4% in the beginning of 2001. What is the cost of the TV set in 2001 ?
Solution:
List price of TV set in 1999 = Rs 17,000
Rate of hike in 2000 = 5%
Rate of decrease in 2001 = 4%
Price of TV set in 2001

Question 8.
Ashish started the business with an initial investment of Rs 5,00,000. In the first year, he incurred a loss of 4%. However, during the second year he earned a profit of 5% which in third year, rose to 10%. Calculate the net profit for the entire period of 3 years.
Solution:
Initial investment = Rs 5,00,000
In the first year, rate of loss = 4%
In the second year, rate of gain = 5%
and in the third year, rate of gain = 10%
Investment after 3 years

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Question 1.
Write the following squares of bionomials as trinomials :

Solution:
Using the formulas
(a + b)² = a² + 2ab + b² and (a – b)² = a² – 2ab + b²
(i) (a + 2)² = (a)² + 2 x a x 2 + (2)²
{(a + b)² = a² + 2ab + b²}
= a² + 4a + 4
(ii) (8a + 3b)² = (8a)² + 2 x 8a * 3b + (3b)² = 64² + 48ab + 9 b²
(iii) (2m+ 1)² = (2m)² + 2 x 2m x1 + (1)²
= 4m² + 4m + 1

Question 2.
Find the product of the following binomials :


Solution:

Question 3.
Using the formula for squaring a binomial, evaluate the following :
(i) (102)²
(ii) (99)²
(iii) (1001)²
(iv) (999)²
(v) (703)²
Solution:
(i) (102)² = (100 + 2)²
= (100)² + 2 x 100 x 2 + (2)²
{(a + b)² = a² + 2ab + b²}
= 10000 + 400 + 4 = 10404
(ii) (99)² = (100 – 1)²
= (100)² – 2 x 100 X 1 +(1)²
{(a – b)² = a² – 2ab + b²}
= 10000 -200+1
= 10001 -200 =9801
(iii) (1001 )² = (1000 + 1)²
{(a + b)² = a² + 2ab + b²}
= (1000)² + 2 x 1000 x 1 + (1)²
= 1000000 + 2000 + 1 = 1002001
(iv) (999)² = (1000 – 1)²
{(a – b)² = a² – 2ab + b²}
= (1000)² – 2 x 1000 x 1 + (1)²
= 1000000 – 2000 + 1
= 1000001 -2000 = 998001

Question 4.
Simplify the following using the formula:
(a – b) (a + b) = a² – b² :
(i) (82)² (18)²
(ii) (467)² (33)²
(iii) (79)² (69)²
(iv) 197 x 203
(v) 113 x 87
(vi) 95 x 105
(vii) 1.8 x 2.2
(viii) 9.8 x 10.2
Solution:
(i) (82)² – (18)² = (82 + 18) (82 – 18)
{(a + b)(a- b) = a² – b²} = 100 x 64 = 6400
(ii) (467)² – (33)² = (467 + 33) (467 – 33)
= 500 x 434 = 217000
(ii) (79)² – (69)² = (79 + 69) (79 – 69)
148 x 10= 1480
(iv) 197 x 203 = (200 – 3) (200 + 3)
= (200)² – (3)²
= 40000-9 = 39991
(v) 113 x 87 = (100 + 13) (100- 13)
= (100)² – (13)²
= 10000- 169 = 9831
(vi) 95 x 105 = (100 – 5) (100 + 5)
= (100)² – (5)²
= 10000 – 25 = 9975
(vii) 8 x 2.2 = (2.0 – 0.2) (2.0 + 0.2)
= (2.0)² – (0.2)²
= 4.00 – 0.04 = 3.96
(viii)9.8 x 10.2 = (10.0 – 0.2) (10.0 + 0.2)
(10.0)² – (0.2)²
= 100.00 – 0.04 = 99.96

Question 5.
Simplify the following using the identities :

Solution:

Question 6.
Find the value of x, if
(i)  4x = (52)² – (48)²
(ii) 14x = (47)² – (33)²
(iii)  5x = (50)² – (40)²
Solution:
(i) 4x = (52)² – (48)²
⇒ 4x = (52 + 48) (52 – 48)

Question 7.
If x + \(\frac { 1 }{ x }\)= 20, find the value of x²+ \(\frac { 1 }{ { x }^{ 2 } }\)

Solution:

Question 8.
If x – \(\frac { 1 }{ x }\) = 3, find the values of x² + \(\frac { 1 }{ { x }^{ 2 } }\) and x⁴ + \(\frac { 1 }{ { x }^{ 4 } }\)

Solution:

Question 9.
If x² – \(\frac { 1 }{ { x }^{ 2 } }\)= 18, find the values of x+ \(\frac { 1 }{ x }\)  and x– \(\frac { 1 }{ x }\)
Solution:

Question 10.
Ifx+y = 4 and xy = 2, find the value of x²+y².
Solution:
x + y = 4
Squaring on both sides,
(x + y)² = (4)²
⇒ x² +y² + 2xy = 16
⇒ x²+y² + 2 x 2 = 16                       (∵ xy = 2)
⇒ x² + y² + 4 = 16
⇒ x²+y² = 16 – 4= 12           ‘
∴ x²+y² = 12

Question 11.
If x-y = 7 and xy = 9, find the value of x²+y².
Solution:
x-y = 7
Squaring on both sides,
(x-y)² = (7)²
⇒ x²+y²-2xy = 49
⇒ x² + y² – 2 x 9 = 49                    (∵ xy = 9)
⇒ x² +y² – 18 = 49
⇒ x² + y² = 49 + 18 = 67
∴ x²+y² = 67

Question 12.
If 3x + 5y = 11 and xy = 2, find the value of 9x² + 25y²
Solution:
3 x + 5y = 11, xy = 2
Squaring on both sides,
(3x + 5y)² = (11)²
⇒ (3x)² + (5y)² + 2 x 3x x 5y = 121
⇒ 9x² + 25y² + 30 x 7 = 121
⇒ 9x² + 25y²+ 30 x 2 = 121           (∵ xy = 2)
⇒ 9x² + 25y² + 60 = 121
⇒ 9x² + 25y² = 121 – 60 = 61
∴ 9x² + 25y² = 61

Question 13.
Find the values of the following expressions :
(i)16x² + 24x + 9, when X’ = \(\frac { 7 }{ 45 }\)
(ii) 64x² + 81y² + 144xy when x = 11 and y = \(\frac { 4 }{ 3 }\)
(iii) 81x² + 16y²-72xy, whenx= \(\frac { 2 }{ 3 }\) andy= \(\frac { 3 }{ 4 }\)
Solution:

Question 14.
If x + \(\frac { 1 }{ x }\) = 9, find the values of x⁴ + \(\frac { 1 }{ { x }^{ 4 } }\).
Solution:

Question 15.
If x + \(\frac { 1 }{ x }\) = 12, find the values of x–  \(\frac { 1 }{ x }\).
Solution:

Question 16.
If 2x + 3y = 14 and 2x – 3y = 2, find the value of xy.
Solution:
2x + 3y = 14, 2x – 3y= 2
We know that
(a + b)² – (a – b)² = 4ab
∴ (2x + 3y)² – (2x – 3y)² = 4 x 2x x 3y = 24xy
⇒ (14)² – (2)² = 24xy
⇒ 24xj= 196-4= 192
⇒ xy = \(\frac { 192 }{ 24 }\) = 8
∴  xy = 8

Question 17.
If x² + y² = 29 and xy = 2, find the value of
(i) x+y
(ii) x-y
(iii) x⁴ +y⁴
Solution:
x² + y² = 29, xy = 2
(i) (x + y)² = x² + y² + 2xy
= 29 + 2×2 = 29+ 4 = 33
∴  x + y= ±√33
(ii) (x – y)² = x² + y² – 2xy
= 29- 2×2 = 29- 4 = 25
∴ x-y= ±√25= ±5
(iii) x² + y² = 29
Squaring on both sides,
(x² + y²)² = (29)²
⇒ (x²)² + (y²)² + 2x²y² = 841
⇒ x⁴ +y + 2 (xy)² = 841
⇒ x⁴ + y + 2 (2)² = 841          (∵ xy = 2)
⇒ x⁴ + y + 2×4 = 841
⇒ x⁴ + y + 8 = 841
⇒ x⁴ + y = 841 – 8 = 833
∴ x⁴ +y = 833

Question 18.
What must be added to each of the following expressions to make it a whole square ?’
(i) 4x² – 12x + 7
(ii) 4x² – 20x + 20
Solution:
(i) 4x² – 12x + 7 = (2x)² – 2x 2x x 3 + 7
In order to complete the square,
we have to add  3² – 7 = 9 – 7 = 2
∴ (2x)² – 2 x 2x x 3 + (3)²
= (2x-3)²
∴ Number to be added = 2
(ii) 4x² – 20x + 20
⇒ (2x)² – 2 x 2x x 5 + 20
In order to complete the square,
we have to add (5)² – 20 = 25 – 20 = 5
∴ (2x)² – 2 x 2x x 5 + (5)²
= (2x – 5)²
∴ Number to be added = 5

Question 19.
Simplify :
(i) (x-y) (x + y) (x² + y²) (x⁴ + y⁴)
(ii) (2x – 1) (2x + 1) (4x² + 1) (16x⁴ + 1)
(iii) (7m – 8m)² + (7m + 8m)²
(iv) (2.5p -5q)² – (1.5p – 2.5q)²
(v) (m² – n²m)² + 2m³n²
Solution:
(i) (x – y) (x + y) (x² + y²) (x⁴ +y)
= (x² – y²) (x² + y) (x⁴ + y⁴)
= [(x²)² – (y²)²] (x⁴+y⁴)
= (x⁴-y⁴) (x⁴+y⁴)
= (x⁴)² – (y⁴)² = x⁸ – y⁸
(ii) (2x – 1) (2x + 1) (4x² + 1) (16x⁴ + 1)
= [(2x)² – (1)²] (4x² + 1) (16x⁴ + 1)
= (4x² – 1) (4x² + 1) (16x⁴ + 1)
= [(4x²)²-(1)²] (16x⁴+ 1)
= (16x⁴-1) (16x⁴+ 1)
= (16x⁴)²– (1)² = 256x⁸ – 1
(iii) (7m – 8m)² + (7m + 8n)²
= (7m)² + (8n)² – 2 x 7m x 8n + (7m)² + (8n)² + 2 x 7m x 8n
= 49m² + 64m² – 112mn + 49m² + 64m² + 112mn
= 98 m² + 128n²
(iv) (2.5p – 1.5q)² – (1.5p – 2.5q)²
= (2.5p)² + (1.5q)² – 2 x 2.5p x 1.5q
= [(1.5p)² + (1.5q)² – 2 x 1.5 p x 2.5q]
= (6.25p² + 2.25q² – 7.5 pq) – (2.25p² + 6.25q²-7.5pq)
= 6.25p² + 2.25q² – 7.5pq – 2.25p² – 6.25q² + 7.5pq
= 6.25p² – 2.25p² + 2.25g² – 6.25q²
= 4.00P² – 4.00_q²
= 4p² – 4q² = 4 (p² – q²)
(v) (m² – n²m)² + 2m³M²
= (m²)² + (n²m)² -2 x m² x n²m + 2;m³m²
= m⁴ + n⁴m² – 2m³n² + 2m³n²
= m⁴ + n⁴m² = m⁴ + m²n⁴

Question 20.
Show that :

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.1
• RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.2

Question 1.
Which among the following are nets for a cube ?

Solution:
Nets for a cube are (ii), (iv) and (vi)

Question 2.
Name the polyhedron that can be made by folding each net:

Solution:
(i) This net is for a square

(ii) This net is for triangular prism.

(iii) This net is for triangular prism.

(iv) This net is for hexagonal prism.

(v) This net is for hexagon pyramid.

(vi) This net is for cuboid.

Question 3.
Dice are cubes where the numbers on the opposite faces must total 7. Which of the following are dice ?


Solution:
Figure (i) shows the net of cube or dice.

Question 4.
Draw nets for each of the following polyhedrons:


Solution:
(i) Net for cube is given below :

(ii) Net of a triangular prism is as under :

(iii) Net of hexagonal prism is as under :

(iv) The net for pentagonal pyramid is as under:

Question 5.
Match the following figures:


Solution:
(a) (iv)
(b) (i)
(c) (ii)
(d) (iii)

Hope given RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.1
• RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.2

Question 1.
What is the least number of planes that can enclose a solid ? What is the name of the solid ?
Solution:
The least number of planes that can enclose a solid is called a Tetrahedron.

Question 2.
Can a polyhedron have for its faces :
(i) three triangles ?
(ii) four triangles ?
(iii) a square and four triangles ?
Solution:
(i) No, polyhedron has three faces.
(ii) Yes, tetrahedron has four triangles as its faces.
(iii) Yes, a square pyramid has a square as its base and four triangles as its faces.

Question 3.
Is it possible to have a polyhedron with any given number of faces ?
Solution:
Yes, it is possible if the number of faces is 4 or more.

Question 4.
Is a square prism same as a cube ?
Solution:
Yes, a square prism is a cube.

Question 5.
Can a polyhedron have 10 faces, 20 edges and 15 vertices ?
Solution:
No, it is not possible as By Euler’s formula
F + V = E + 2
⇒ 10 + 15 = 20 + 2
⇒ 25 = 22
Which is not possible

Question 6.
Verify Euler’s formula for each of the following polyhedrons :

Solution:
(i) In this polyhedron,
Number of faces (F) = 7
Number of edges (E) = 15
Number of vertices (V) = 10
According to Euler’s formula,
F + V = E + 2
⇒ 7 + 10 = 15 + 2
⇒ 17 = 17
Which is true.
(ii) In this polyhedron,
Number of faces (F) = 9
Number of edges (E) = 16
Number of vertices (V) = 9
According to Euler’s formula,
F + V = E + 2
⇒ 9 + 9 = 16 + 2
⇒ 18 = 18
Which is true.
(iii) In this polyhedron,
Number of faces (F) = 9
Number of edges (E) =18
Number of vertices (V) = 11
According to Euler’s formula,
F + V = E + 2
⇒ 9 + 11 = 18 + 2
⇒ 20 = 20
Which is true.
(iv) In this polyhedron,
Number of faces (F) = 5
Number of edges (E) = 8
Number of vertices (V) = 5
According to Euler’s formula,
F + V = E + 2
⇒ 5 + 5 = 8 + 2
⇒ 10 = 10
Which is true.
(v) In the given polyhedron,
Number of faces (F) = 9
Number of edges (E) = 16
Number of vertices (V) = 9
According to Euler’s formula,
F + V = E + 2
⇒ 9 + 9 = 16 + 2
⇒ 18 = 18
Which is true.

Question 7.
Using Euler’s formula, find the unknown:

Solution:
We know that Euler’s formula is
F + V = E + 2
(i) F + 6 = 12 + 2
⇒ F + 6 = 14
⇒ F = 14 – 6 = 8
Faces = 8
(ii) F + V = E + 2
⇒ 5 + V = 9 + 2
⇒ 5 + V = 11
⇒ V = 11 – 5 = 6
Vertices = 6
(iii) F + V = E + 2
⇒ 20 + 12 = E + 2
⇒ 32 = E + 2
⇒ E = 32 – 2 = 30
Edges = 30

Hope given RD Sharma Class 8 Solutions Chapter 19 Visualising Shapes Ex 19.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
Construct a quadrilateral ABCD given that AB = 4 cm, BC = 3 cm, ∠A = 75°, ∠B = 80° and ∠C = 120°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4 cm.

(ii) At A draw a ray AX making an angle of 75°.
(iii) At B draw another ray BY making an angle of 80° and cut off BC = 3 cm.
(iv) At C, draw another ray CZ making an angle of 120° which intersects AX at D.
Then ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD where AB = 5.5 cm, BC = 3.7 cm, ∠A = 60°, ∠B = 105° and ∠D = 90°.
Solution:
∠A = 60°, ∠B = 105° and ∠D = 90°
But ∠A + ∠B + ∠C + ∠D = 360° (Sum of angles of a quadrilateral)
⇒ 60° + 105° + ∠C + 90° = 360°
⇒ 255° + ∠C = 360°
⇒ ∠C = 360° – 255° = 105°
Steps of construction :
(i) Draw a line segment AB = 5.5 cm.
(ii) At A, draw a ray AX making an angle of

(iii) At B, draw another ray BY making an angle of 105° and cut off BC = 3.7 cm.
(iv) At C, draw a ray CZ making an angle of 105° which intersects AX at D.
Then ABCD is the required quadrilateral.

Question 3.
Construct a quadrilateral PQRS where PQ = 3.5 cm, QR = 6.5 cm, ∠P = ∠R = 105° and ∠S = 75°.
Solution:
∠P = 105°, ∠R = 105° and ∠S = 75°
But ∠P + ∠Q + ∠R + ∠S = 360° (Sum of angles of a quadrilateral)
⇒ 105° + ∠Q + 105° + 75° = 360°
⇒ 285° + ∠Q = 360°
⇒ ∠Q = 360° – 285° = 75°
Steps of construction :
(i) Draw a line segment PQ = 3.5 cm.

(ii) At P, draw a ray PX making an angle of 105°.
(iii) At Q, draw another ray QY, making an angle of 75° and cut off QR = 6.5 cm.
(iv) At R, draw a ray RZ making an angle of 105° which intersects PX at S.
Then PQRS is the required quadrilateral.

Question 4.
Construct a quadrilateral ABCD when BC = 5.5 cm, CD = 4.1 cm, ∠A = 70°, ∠B = 110° and ∠D = 85°.
Solution:
∠A = 70°, ∠B = 110°, ∠D = 85°
But ∠A + ∠B + ∠C + ∠D = 360° (Sum of angles of a quadrilateral)
⇒ 70° + 110° + ∠C + 85° = 360°
⇒ 265° + ∠C = 360°
⇒ ∠C = 360° – 265° = 95°
Steps of construction:
(i) Draw a line segment BC = 5.5 cm.
(ii) At B, draw a ray BX making an angle of 110°.
(iii) At C, draw another ray CY making an angle of 95° and cut off CD = 4.1 cm.
(iv) At D, draw a ray DZ making an angle of 85° which intersects BX at A.

Then ABCD is the required quadrilateral.

Question 5.
Construct a quadrilateral ABCD, where ∠A = 65°, ∠B = 105°, ∠C = 75°, BC = 5.7 cm and CD = 6.8 cm.
Solution:
∠A = 65°, ∠B = 105°, ∠C = 75°
But ∠A + ∠B + ∠C + ∠D = 360° (Sum of angles of a quadrilateral)
⇒ 65° + 105° + 75° + ∠D = 360°
⇒ 245° + ∠D = 360°
⇒ ∠D = 360° – 245° = 115°
Steps of construction:
(i) Draw a line segment BC = 5.7 cm.
(ii) At B, draw a ray BX making an angle of

(iii) At C draw a another ray CY making an angle of 75° and cut off CD = 6.8 cm.
(iv) At D, draw a ray DZ making an angle of 115° which intersects BX at A.
Then ABCD is the required quadrilateral.

Question 6.
Construct a quadrilateral PQRS in which PQ = 4 cm, QR = 5 cm, ∠P = 50°, ∠Q = 110° and ∠R = 70°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 4 cm.
(ii) At P, draw a ray PX making an angle of 50°.
(iii) At Q, draw another ray QY making an angle of 110° and cut off QR = 5 cm.
(iv) At R, draw a ray RZ making an angle of 70° which intersects PX at S.

Then PQRS is the required quadrilateral.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
Construct a quadrilateral ABCD, in which AB = 6 cm, BC = 4 cm, CD = 4 cm, ZB = 95° and ∠C = 90°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4 cm.

(ii) At B, draw a ray BX making an angle of 95° and cut off BA = 6 cm.
(iii) At C, draw a ray CY making an angle of 90° and cut off CD = 4 cm.
(iv) Join AD.
Then ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD, where AB = 4.2 cm, BC = 3.6 cm, CD = 4.8 cm, ∠B = 30° and ∠C = 150°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.6 cm.
(ii) At B, draw a ray BX making an angle of 30° and cut of BA = 4.2 cm.
(iii) At C, draw another ray CY making an angle of 150° and cut off CD = 4.8 cm.

(iv) Join AD.
Then ABCD is the required quadrilateral.

Question 3.
Construct a quadrilateral PQRS, in which PQ = 3.5 cm, QR = 2.5 cm, RS = 4.1 cm, ∠Q = 75° and ∠R = 120°.
Solution:
Steps of construction :
(i) Draw a line segment QR = 2.5 cm.

(ii) At Q, draw a ray QX making an angle of 75° and cut off QP = 3.5 cm.
(iii) At R, draw another ray RY making an angle of 120° and cut off RS = 4.1 cm.
(iv) Join PS.
Then PQRS is the required quadrilateral.

Question 4.
Construct a quadrilateral ABCD given BC = 6.6 cm, CD = 4.4 cm, AD = 5.6 cm and ∠D = 100° and ∠C = 95°.
Solution:
Steps of construction :
(i) Draw a line segment CD = 4.4 cm.

(ii) At C, draw a ray CX making an angle of 95° and cut off CB = 6.6 cm
(iii) At D, draw another ray DY making an angle of 100° and cut off DA = 5.6 cm.
(iv) Join AB.
Then ABCD is the required quadrilateral.

Question 5.
Construct a quadrilateral ABCD in which AD = 3.5 cm, AB = 4.4 cm, BC = 4.7 cm, ∠A = 125° and ∠B = 120°.
Solution:
Steps of construction :
(i) Draw a line segment AB 4.4 cm.

(ii) At A, draw a ray AX making an angle of 125° and cut off AD = 3.5 cm.
(iii) At B, draw another ray BY making an angle of 120° and cut off BC = 4.7 cm.
(iv) Join CD.
Then ABCD is the required quadrilateral.

Question 6.
Construct a quadrilateral PQRS in which ∠Q = 45°, ∠R = 90°, QR = 5 cm, PQ = 9 cm and RS = 7 cm.
Solution:
Steps of construction :
This quadrilateral is not possible to construct as shown in the figure.

Question 7.
Construct a quadrilateral ABCD in which AB = BC = 3 cm, AD = 5 cm, ∠A = 90° and ∠B = 105°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 3 cm.

(ii) At A, draw a ray AX making an angle of 90° and cut off AD = 5 cm.
(iii) At B, draw another ray BY making an angle of 105° and cut off BC = 3 cm.
(iv) Join CD.
Then ABCD is the required quadrilateral.

Question 8.
Construct a quadrilateral BDEF where DE = 4.5 cm, EF = 3.5 cm, FB = 6.5 cm and ∠F = 50° and ∠E = 100°
Solution:
Steps of construction :
(i) Draw a line segment EF = 3.5 cm.
(ii) At E, draw a ray EX making an angle of 100° and cut off ED = 4.5 cm.
(iii) At F, draw another ray FY making an angle of 45° and cut off FB = 6.5 cm.
(iv) Join DB.

Then BDEF is the required quadrilateral.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.4 cm, CD = 4.5 cm, AD = 5 cm and ∠B = 80°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 3.8 cm.
(ii) At B, draw a ray BX making an angle of 80° and cut off BC = 3.4 cm.
(iii) With centre A and radius 5 cm and with centre C and radius 4.5 cm, draw arcs which intersect each other at D.
(iv) Join CD and AD.

ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD given that AB = 8 cm, BC = 8 cm, CD = 10 cm, AD = 10 cm and ∠A = 45°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8 cm.

(ii) At A, draw a ray AX making an angle of 45° and cut off BC = 8 cm.
(iii) With centre A and C and radius 10 cm, draw arcs intersecting each other at D.
(iv) Join AD, CD.
Then ABCD is the required quadrilateral.

Question 3.
Construct a quadrilateral ABCD in which AB = 7.7 cm, BC = 6.8 cm, CD = 5.1 cm, AD = 3.6 cm and ∠C = 120°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6.8 cm.

(ii) At C, draw a ray CX making an angle of 120° and cut off CD = 5.1 cm.
(iii) With centre B and radius 7.7 cm and with centre D and radius 3.6 cm draw arcs which intersect each other at A.
(iv) Join AD and AB.
Then ABCD is the required quadrilateral.

Question 4.
Construct a quadrilateral ABCD in which AB = BC = 3 cm, AD = CD = 5 cm and ∠B = 120°
Solution:
Steps of construction :
(i) Draw a line segment AB = 3 cm.

(ii) At B, draw a ray BX making an angle of 120° and cut off BC = 3 cm.
(iii) With centres A and C, and radius 5 cm, draw arcs intersecting each other at D.
(iv) Join AD and CD.
Then ABCD is the required quadrilateral.

Question 5.
Construct a quadrilateral ABCD in which AB = 2.8 cm, BC = 3.1 cm, CD = 2.6 cm and DA = 3.3 cm and ∠A = 60°.
Solution:
Steps of construction :
(i) Draw a line segment AB = 2.8 cm.

(ii) At A draw a ray AX making an angle of 60° and cut off AD = 3.3 cm.
(iii) With centre B and radius 3.1 cm and with centre D and radius 2.6 cm, draw arc which intersect each other at C.
(iv) Join CB and CD.
Then ABCD is the required quadrilateral.

Question 6.
Construct a quadrilateral ABCD in which AB = BC = 6 cm, AD = DC = 4.5 cm and ∠B = 120°.
Solution:
Steps of construction:
The construction is not possible to draw as arcs of radius 4.5 cm from A and C, do not intersect at any point.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.