Category: CBSE Class 8

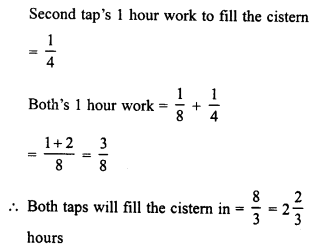
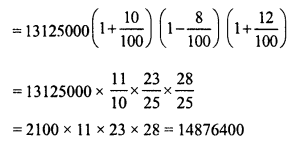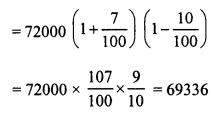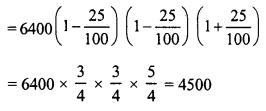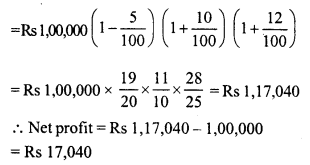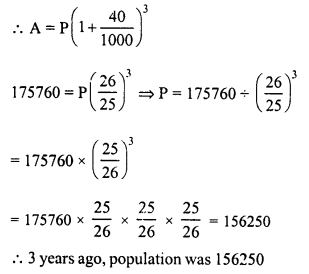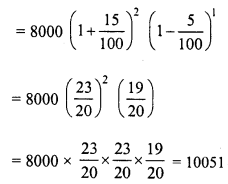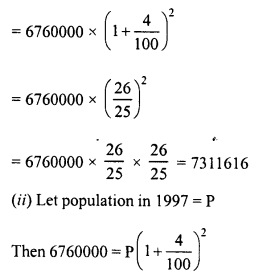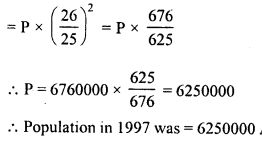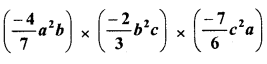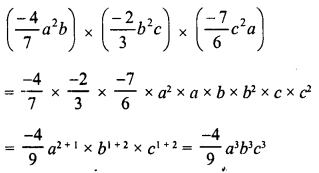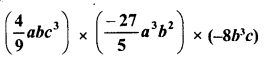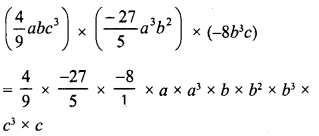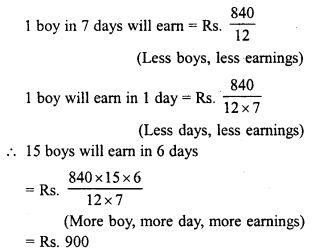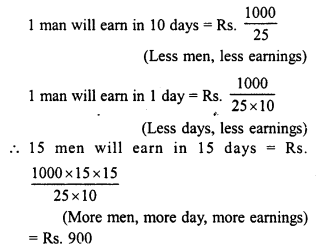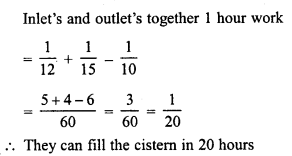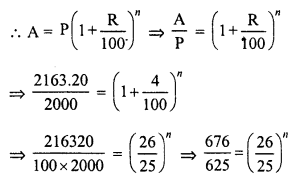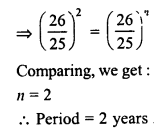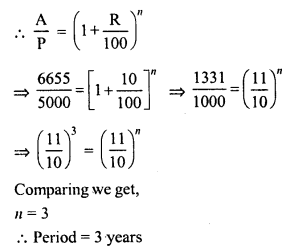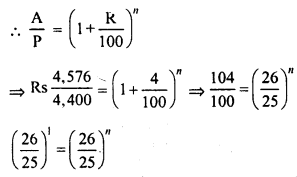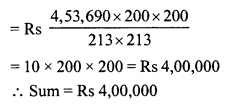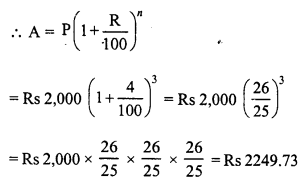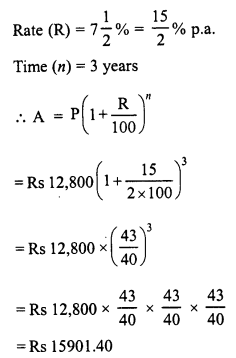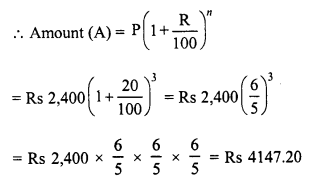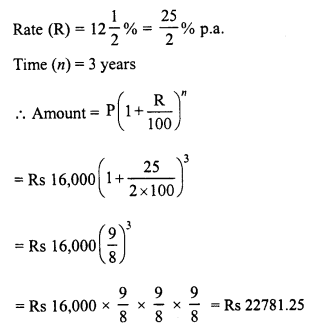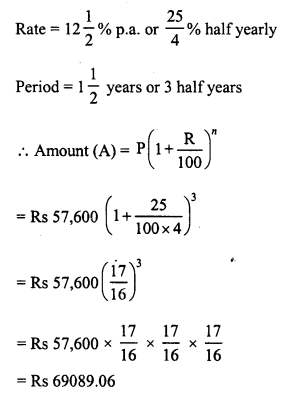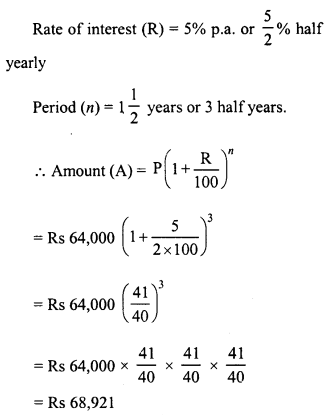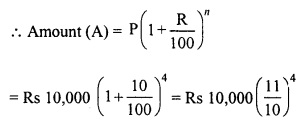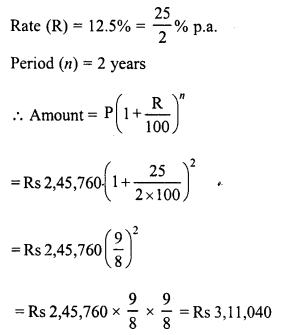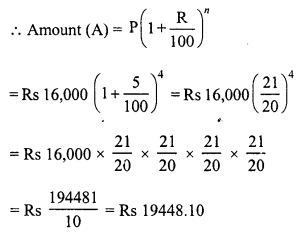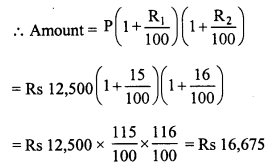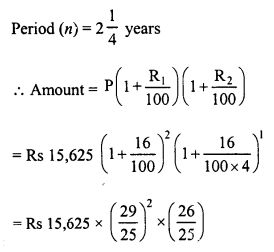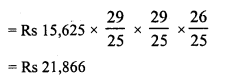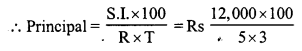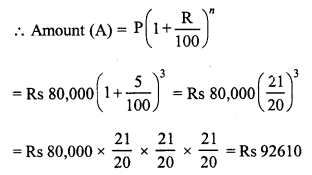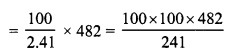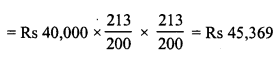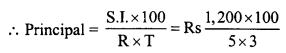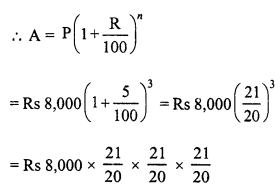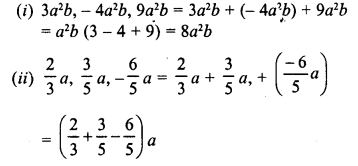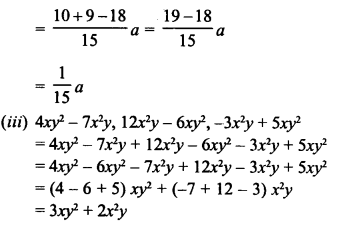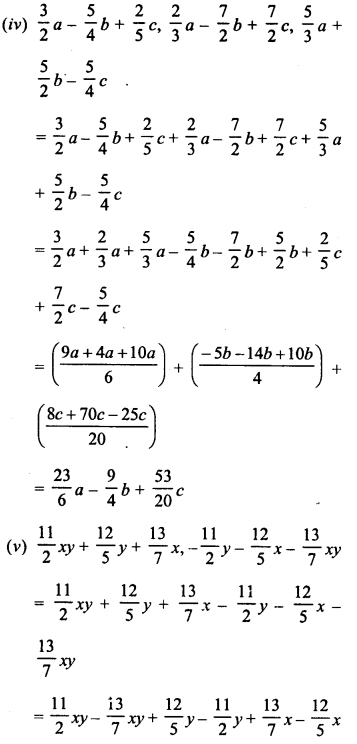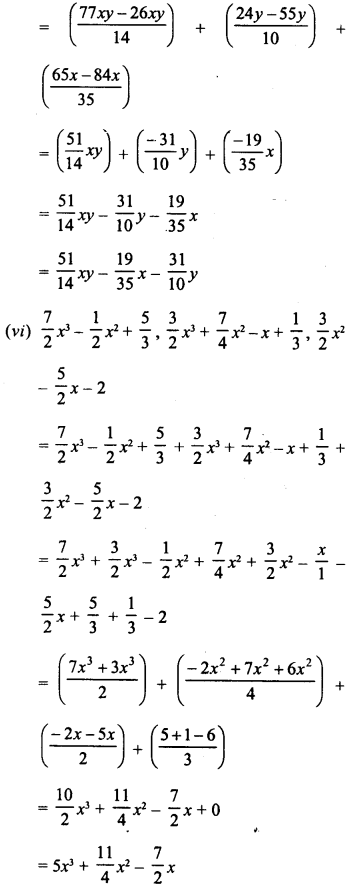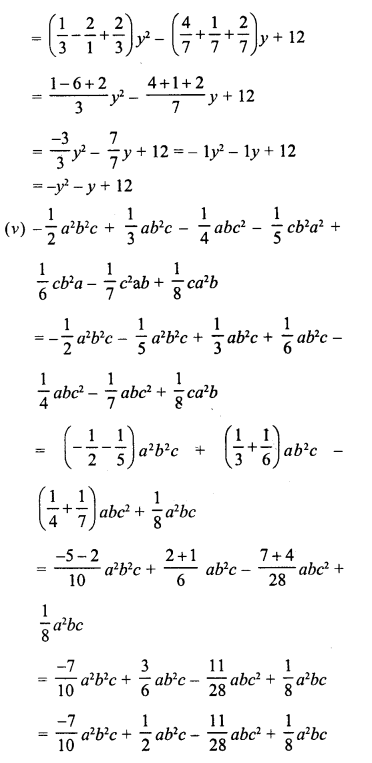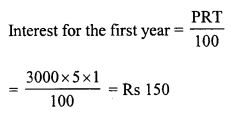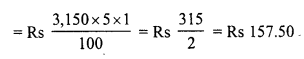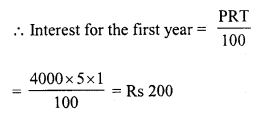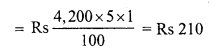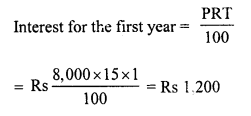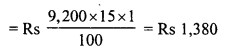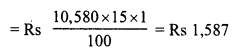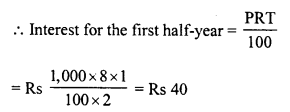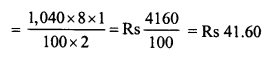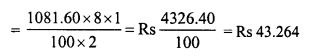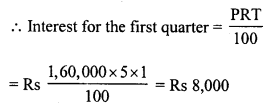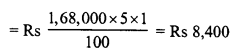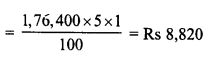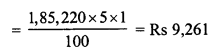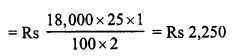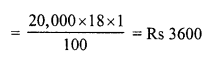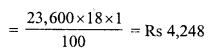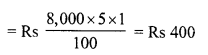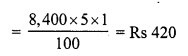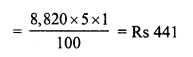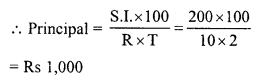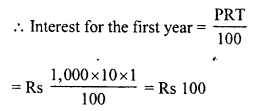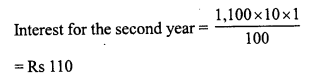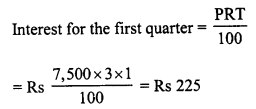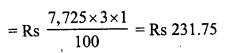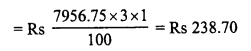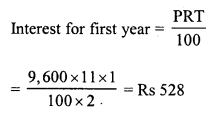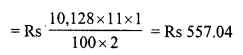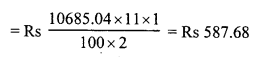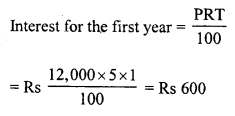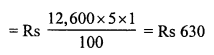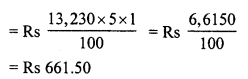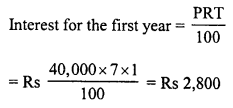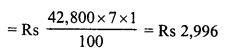RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.1
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.2
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.3

Question 1.
A student buys a pen for Rs. 90 and sells it for Rs. 100. Find his gain and gain percent ?
Solution:
C.P. of a pen = Rs. 90
and S.P. = Rs. 100
Gain = S.P. – C.P. = Rs. 100 – 90 (S.P > C.P.)
= Rs. 10

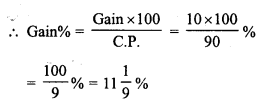
Question 2.
Rekha bought a saree for Rs. 1240 and sold it for Rs. 1147. Find her loss and loss percent.
Solution:
C.P. of saree.= Rs. 1240 and
S.P. = Rs. 1147
Loss = C.P – S.P. = Rs. 1240 – Rs. 1147 (C.P. > S.P.)
= Rs. 93

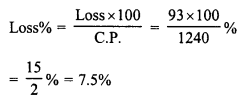
Question 3.
A boy buys 9 apples for Rs. 9.60 and sells them at 11 for Rs. 12. Find his gain or loss percent.
Solution:
L.C.M. of 9 and 11 = 99
Let 99 apples were purchased.
C.P. of 99 apples at the rate of 9 apples for Rs. 9.60

Question 4.
The cost price of 10 articles is equal to the selling price of 9 articles. Find the profit percent.
Solution:
C.P. of 10 articles = S.P. of 9 articles = 90 (Suppose)

Question 5.
A retailer buys a radio for Rs. 225. His overhead expenses are Rs. 15. If he sells the radio for Rs. 300, determine his profit percent.
Solution:
Cost of radio = Rs. 225
Over head expenses = Rs. 15
Total C.P. of the ratio = Rs. 225 + 15 = Rs. 240
S.P. of radio = Rs. 300
Gain = S.P. – C.P. = Rs. 300 – Rs. 240 = Rs. 60

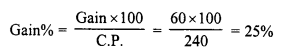
Question 6.
A retailer buys a cooler for Rs. 1200 and overhead expenses on it are Rs. 40. If he sells the cooler for Rs. 1550, determine his profit percent.
Solution:
Cost of cooler = Rs. 1200
Overhead expenses = Rs. 40
Total cost price of cooler = Rs. 1200 + Rs. 40 = Rs. 1240
Selling price = Rs. 1550
Gain = S.P. – C.P. = Rs. 1550 – Rs. 1240 = Rs. 310

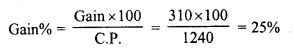
Question 7.
A dealer buys a wristwatch for Rs. 225 and spends Rs. 15 on its repairs. If he sells the same for Rs. 300, find his profit percent.
Solution:
Cost of wristwatch = Rs. 225
Cost on repairs = Rs. 15
Total cost price = Rs. 225 + Rs. 15 = Rs. 240
Selling price = Rs. 300
Gain = S.P. – C.P. = Rs. 300 – Rs. 240 = Rs. 60

Question 8.
Ramesh bought two boxes for Rs. 1300. He sold one box at a profit of 20% and the other box at a loss of 12%. If the selling price of both boxes is the same, find the cost price of each box.
Solution:
Total cost price of two boxes = Rs. 1300
S.P. of each box is same.
Let S.P of each box = Rs. 100
S.P. of first box = Rs. 100
Gain = 20%

Question 9.
If the selling price of 10 pens is equal to cost price of 14 pens, find the gain percent.
Solution:
S.P. of 10 pens = C.P. of 14 pens = Rs. 100 (Suppose)

Question 10.
If the cost price of 18 chairs be equal to selling price of 16 chairs, And the gain or loss percent.
Solution:
C.P. of 18 chairs = S.P. of 16 chairs = Rs. 100 (Suppose)

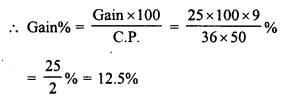
Question 11.
If the selling price of 18 oranges is equal to the cost price of 16 oranges, And the loss percent.
Solution:
S.P. of 18 oranges = C.P. of 16 oranges = Rs. 100 (Suppose)

Question 12.
Ravish sold his motorcycle to Vineet at a loss of 28%. Vineet spent Rs. 1680 on its repairs and sold the motor cycle to Rahul for Rs. 35910, thereby making a profit of 12.5%, find the cost price of the motor cycle for Ravish.
Solution:
Cost price of cycle for Rahul or Selling price for Vineet = Rs. 35910
Gain = 12.5%

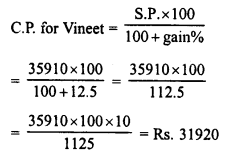
Question 13.
By selling a book for Rs. 258, a book-seller gains 20%. For how much should he sell it to gain 30% ?
Solution:
S.P. of a book = Rs. 258
Gain = 20%

Question 14.
A defective briefcase costing Rs. 800 is being sold at a loss of 8%. If its price is further reduced by 5%, find its selling price.
Solution:
C.P. of a briefcase = Rs. 800
Loss = 8%

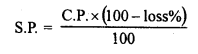
Question 15.
By selling 90 ball pens for Rs. 160, a person losses 20%. How many ball pens should be sold for Rs. 96 so as to have a profit of 20%.
Solution:
S.P of 90 ball pens = Rs. 160

Question 16.
A man sells an article at a profit of 25%. If he had bought it at 20% less and sold it for Rs. 36.75 less, he would have gained 30%. Find the cost price of the article.
Solution:
Let C.P. of the article = Rs. 100
In first case gain = 25%
S.P. = 100 + 25 = Rs. 125
In second case,
C.P. = 20% less of Rs. 100 = 100 – 20 = Rs. 80
Gain = 30%

Question 17.
A dishonest shopkeeper professes to sell pulses at his cost price but uses a false weight of 950 for each kilogram. Find his gain percent.
Solution:
Let C.P. of 1 kg of pulses = Rs. 100
S.P. of 950 gm = Rs. 100

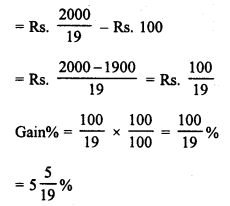
Question 18.
A dealer bought two tables for Rs. 3120. He sold one of them at a loss of 15% and other at a gain of 36%. Then he found that each table was sold for the same price, find the cost price of each table.
Solution:
Cost price of two tables = Rs. 3120
Let S.P of each table = Rs. 100
Now S.P of one table = Rs. 100
Loss = 15%

Question 19.
Mariam bought two fans for Rs. 3605. She sold one at a profit of 15% and the other at a loss of 9%. If Mariam obtained the same amount for each fan, find the cost price of each fan.
Solution:
Total cost price of two fans = Rs. 3605
Let selling price of each fan = Rs. 100
Now S.P. of first fan = Rs. 100
Profit = 15%

Question 20.
Some toffees are bought at the rate of 11 for Rs. 10 and the same number at the rate of 9 for Rs. 10. If the whole lot is sold at one rupee per toffee, find the gain or loss percent on the whole transaction.
Solution:
L.C.M. of 11 and 9 = 99
Let each time 99 toffees are bought.
In first case, the C.P. of 99 toffees at the rate of 11 for Rs. 10

Question 21.
A tricycle is sold at a gain of 16%. Had it been sold for Rs. 100 more, the gain would have been 20%. Find the C.P. of the tricycle.
Solution:
Let the C.P. of tricycle = Rs. 100
In first case, gain = 16%
S.P. = Rs. 100 + 16 = Rs. 116
In second case, gain = 20%
S.P. = Rs. 100 + 20 = Rs. 120
Difference in S.P.’s = Rs. 120 – Rs. 116 = Rs. 4
If difference is Rs. 4,
then C.P. of the tricycle = Rs. 100
and if difference is Re. 1, then C.P.

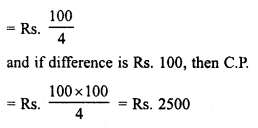
Question 22.
Shabana bought 16 dozen ball pens and sold then at a loss equal to S.P. of 8 ball pens. Find
(i) her loss percent
(ii) S.P. of 1 dozen ball pens, if she purchased these 16 dozen ball pens for Rs. 576.
Solution:
C.P. of 16 dozen ball pens = S.P. of 16 dozen pens – loss
C.P. of 16 x 12 pens = S.P. of 16 dozen pens x S.P. of 8 pens
C.P. of 192 pens = S.P. of 16 x 12 pens x S.P. of 8 pens
S.P. of 192 pens + S.P. of 8 pens = S.P. of 200 pens
(i) Let C.P. of 1 pen = Re. 1
Then C.P. of 192 pens = Rs. 192
and S.P. of 200 pens = Rs. 192

Question 23.
The difference between two selling prices of a shirt at profits of 4% and 5% is Rs. 6. Find
(i) C.P. of the shirt
(ii) The two selling prices of the shirt
Solution:
The difference of two selling prices of shirt = Rs. 6
Difference in profits of 4% and 5% = 5 – 4 = 1%
(i) C.P. = 1 x 6 x 100 = Rs. 600

Question 24.
Toshiba bought 100 hens for Rs. 8000 and sold 20 of these at a gain of 5%. At what gain percent she must sell the remaining hens so as to gain 20% on the whole ?
Solution:
Total number of hens bought = 100
C.P. of 100 hens = Rs. 8000

Hope given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.1
• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.2
• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.3

Question 1.
Without performing actual addition and division, write the quotient when the sum of 69 and 96. is divided by
(i) 11
(ii) 15
Solution:
Two numbers are 69 and 96 whose digits are reversed Here a = 6,= 9
(i) Sum if 69 + 96 is divisible by 11, then quotient = a + 6 = 6 + 9 = 15
(ii) If it is divided by a + b i.e., 6 + 9 = 15, then quotient = 11

Question 2.
Without performing actual computations, find the quotient when 94 – 49 is divided by
(i) 9
(ii) 5
Solution:
Two given numbers are 94 and 49. Whose digits are reversed.
(i) If 94 – 49 is divided by 9, then the quotient = a-b = 9-4 = 5
(ii) and when it is divided by a – b i.e. 9-4 = 5, then quotient will be = 9

Question 3.
If sum of the number 985 and two other numbers obtained by arranging the digits of 985 in cyclic order is divided by 111, 22 and 37 respectively. Find the quotient in each case.
Solution:
The given number is 985
The other two numbers by arranging its digits
in cyclic order, will be 859, 598 of the form
\(\overline{ abc } ,\overline{ bca } ,\overline{ cba }\)
Therefore,
If 985 + 859 + 598 is divided by 111, then quotient will bea + 6 + c = 9 + 8 + 5 = 22
If this sum is divided by 22, then the quotient = 111
and if it is divided by 37, then quotient = 3 (a + b + c) = 3 (22) = 66

Question 4.
Find the quotient when difference of 985 and 958 is divided by 9.
Solution:
The numbers of three digits are
985 and 958 in which tens and ones digits are reversed, then
\(\overline{ abc } -\overline{ acb }\) = 9 (b – c)
985 – 958 = 9 (8 – 5) = 9 x 3
i. e., it is divisible by 9, then quotient = b-c =8-5=3

 

Hope given RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 12 Percentage Ex 12.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 12 Percentage Ex 12.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 12 Percentage Ex 12.1
• RD Sharma Class 8 Solutions Chapter 12 Percentage Ex 12.2

Question 1.
Write each of the following as percent: Solution—
(i) \(\frac { 7 }{ 25 }\)
(ii) \(\frac { 16 }{ 625 }\)
(iii) \(\frac { 5 }{ 8 }\)
(iv) 0.8
(v) 0.005
(vi) 3 : 25
(vii) 11 : 80
(viii) 111 : 125
(ix) 13 : 75
(x) 15 : 16
(xi) 0.18
(xii) \(\frac { 7 }{ 125 }\)
Solution:

Question 2.
Convert the following percentages to fractions and ratios :
(i) 25%
(ii) 2.5%
(iii) 0.25%
(iv) 0.3%
(v) 125%
Solution:

Question 3.
Express the following as decimal fractions :
(i) 27%
(ii) 6.3%
(iii) 32%
(iv) 0.25%
(v) 7.5%
(vi) \(\frac { 1 }{ 8 }\) %
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 12 Percentage Ex 12.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
The present population of a town is 28,000. If it increases at the rate of 5% per annum, what will be its population after 2 years ?
Solution:
Present population = 28000
Rate of increase (R) = 5% p.a.
Period (n) = 2 years
Population after 2 years

Question 2.
The population of a city is 125000. If the annual birth rate and death rate are 5.5% and 3.5% respectively, calculate the population of city after 3 years.
Solution:
Present population = 125000
Rate of birth = 5.5%
and rate of death = 3.5%
Increase = 5.5 – 3.5 = 2% p.a.
Period = 3 years.
Population after 3 years

Question 3.
The present population of a town is 25000. It grows at 4%, 5% and 8% during first year, second year and third year respectively. Find its population after 3 years.
Solution:
Present population = 25000
Increase in first year = 4%
in second year= 5% and
in third year = 8%
Population after 3 years =

Question 4.
Three years ago, the population of a town was 50000. If the annual increase during three successive years be at the rate of 4%, 5% and 3% respectively, find the present population.
Solution:
Three years ago,
Population of a town = 50000
Annual increase in population in first year = 4%
in second year = 5%
and in third year = 3%
Present population

Question 5.
There is a continuous growth in population of a village at the rate of 5% per annum. If its present population is 9261, what it was 3 years ago ?
Solution:
Let 3 years ago, population = P
Present population = 9261
Rate of increase (R) = 5% p.a.
Period (n) = 3 years.

Question 6.
In a factory, the production of scooters rose to 46305 from 40000 in 3 years. Find the annual rate of growth of the production of scooters.
Solution:
Production of scooters 3 years ago (P) = 40000
Present production (A) = 46305
Period (n) = 3 years

Question 7.
The annual rate of growth in population of a certain city is 8%. If its present population is 196830, what it was 3 years ago ?
Solution:
Let 3 years ago, the population of a city = P
Rate of growth (R) = 8% p.a.
Present population = 196830
Period (n) = 3 years

Question 8.
The population of a town increases at the rate of 50 per thousand. Its population after 2 years will be 22050. Find its present population.
Solution:
Population after 2 years = 22050
Rate of increase = 50 per thousand
Period (n) = 2 years
Let present population = P, then

Question 9.
The count of bacteria in a culture grows by 10% in the first hour, decreases by 8% in the second hour and again increases by 12% in the third hour. If the count of bacteria in the sample is 13125000, what will be the count of bacteria after 3 hours ?
Solution:
Present count of bacteria = 13125000
In first hour increase = 10%
decrease in second hour = 8%
increase in third hour = 12%
Count of bacteria after 3 hours

Question 10.
The population of a certain city was 72000 on the last day of the year 1998. During next year it increased by 7% but due to an epidemic it decreased by 10% in the following year. What was its population at the end of the year 2000 ?
Solution:
On the last day of 1998,
Population of a town = 72000
In the first year, increase = 7%
In the second year, decrease = 10%
Population in the last day of 2000

Question 11.
6400 workers were employed to construct a river bridge in four years. At the end of the first year, 25% workers were retrenched. At the end of the second year, 25% of those working at that time were retrenched. However, to complete the project in time, the number of workers was increased by 25% at the end of the third year. How many workers were working during the fourth year ?
Solution:
Number of workers at the beginning = 6400
Period = 4 years.
At the end of 1st year, workers retrenched = 25%
At the end of second year, workers retrenched = 25%
At the end of third year, workers increased = 25%
Total number of workers during the 4 years

Question 12.
Aman started a factory with an initial investment of Rs 1,00,000. In the first year, he incurred a loss of 5%. However, during the second year, he earned a profit of 10% which in the third year rose to 12%. Calculate his net profit for the entire period of three years.
Solution:
Initial investment = Rs 100000
Loss in the first year = 5%
Profit in the second year = 10%
Profit in the third year = 12%
Investment at the end of 3 years

Question 13.
The population of a town increases at the rate of 40 per thousand annually. If the present population be 175760, what was the population three years ago ?
Solution:
Present population (A) = 175760
Increase rate = 40 per 1000
Period = 3 years
Let 3 years ago,
population was = P

Question 14.
The production of a mixi company in 1996 was 8000 mixies. Due to increase in demand it increases its production by 15% in the next two years and after two years its demand decreases by 5%. What will be its production after 3 years ?
Solution:
Production of Mixi in 1996 = 8000
Increase in next 2 years = 15%
Decrease in the third year = 5%
Production after 3 years

Question 15.
The population of a city increases each year by 4% of what it had been at the beginning of each year. If the population in 1999 had been 6760000, find the population of the city in (i) 2001 (ii) 1997.
Solution:
Population of a city in 1999 = 6760000
Increase = 4%
(i) Population in 2001 is after 2 years

Question 16.
Jitendra set up a factory by investing Rs 25,00,000. During the first two successive years his profits were 5% and f 10% respectively. If each year the profit was on previous year’s capital, compute his total profit.
Solution:
Investment in the beginning = Rs 25,00,000
Profit during the first 2 years = 5% and 10% respectively
Investment after 2 years will be

= Rs 28,87,500
Amount of profit = Rs 28,87,500 – Rs 25,00,000 = Rs 3,87,500

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Find each of the following products (1-8)
Question 1.
5x² x 4x³
Solution:
5x² x 4x³ = 5 x 4 x x² x x³
= 20x^{2 + 3} = 20x^s

Question 2.
3a² x 4b⁴
Solution:
-3a² x 4b⁴ = -3 x 4 x a²b⁴
= -12a²b⁴

Question 3.
(-5xy) x (-3x²yz)
Solution:
(-5xy) x (-3x²yz)
= (-5) x (-3)xy x x²yz
= 15x^{1 + 2}xy^{1+ 1}z= 15x³y²z

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Find each of the following products : (9-17)

Question 9.
(7ab) x (-5ab²c) x (6abc²)
Solution:
(7ab) x (-5ab²c) x (6abc²)
= 7 x (-5) x 6 x a x a x a x b x b² x b x c x c²
=-210 x a¹⁺¹⁺¹ x b¹⁺²⁺¹x c¹⁺²
=-210 x a³b⁴c³

Question 10.
(-5a) x (-10a²) x (-2a³)
Solution:
(-5a) x (-10a²) x (-2a³)
= (-5) (-10) (-2) x a x a² x a³
= -100a^{1 + 2 + 3} = -100a⁶

Question 11.
(-4x²) x (-6xy²) x (-3yz²)
Solution:
(-4x²) x (-6xy²) x (-3yz²)
= (-4) x (-6) x (-3) x² x x x y² x y xz²
= -72x²⁺¹ x y²⁺¹ x _z²
= 72x³y³z³

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.
(2.3xy) x (0.1x) x (0.16)
Solution:
(2.3xy) x (0.1x) x (0.16)
= 2.3 x 0.1 x 0.16 x x x x x y
= 0.0368x^{1 +1} x y = 0.0368x²y

Express each of the following products as a monomials and verify the result in each case for x = 1 : (18 -26)

Question 18.
(3x) x (4x) x (-5x)
Solution:

Question 19.

Solution:

Question 20.
(5x⁴) x (x²)³ x (2x)²
Solution:
(5x⁴) x (x²)³ x (2x)²
= 5x⁴ x x^{2 x 3} x 2x x 2x
= 5x⁴ * x⁶ x 4x² = 5 x 4 x x^{4 + 6 + 2}
= 20x¹²
Verification:
L.H.S. = (5x⁴) x (x²)³ x (2x)²
= 5 x (1)⁴ x [(1)²]³ x (2 x 1)²
= 5 x 1 x (1)^{2 x 3}_x (2)²
= 5 x 1⁶ x 2² = 5 x 1 x 4 = 20
R.H.S. = 20x¹² = 20 (1)¹² = 20 x 1 = 20
∴ L.H.S. = R.H.S.

Question 21.
(x²)³ x (2x) x (-4x) x 5
Solution:
(x²)³ x (2x) x (-4x) x (5)
= x^{2 x 3} X 2x X (-4x) X 5
= x⁶ x 2x x (-4x) x 5 = 2 x (-4) x 5x^{6+1 +1}
= -40x⁸
Verification
L.H.S. = (x²)³ x (2x) x (-4x) x (5)
= (1²)³ x (2 x 1) x (-4 x 1) x 5
= 1^2 x 3 x 2 x (- 4) x 5 = 1⁶ x 2 x (-4) x 5
= 1 x 2 x (-4) x 5 = -40
R.H.S. = -40x⁸ = -40 x (1)⁸
= -40 x 1 = -40
∴ L.H.S. = R.H.S.

Question 22.
Write down the product of -8x²y⁶ and – 20xy Verify the product for x = 2.5, y = 1.
Solution:
Product of -8x²y⁶ and -20xy
= (-8x²y⁶) x (-20xy)
= -8 x (-20) x² x _x x y⁶ x y = 160x^{2 + 1} x y^{6 + 1}
= 160x³y³
Verification.
L.H.S. = (-8x²y⁶) x (-20xy)
= -8 x (2.5)² x (1) x (-20 x 2.5 x 1)
= -8 x 6.25 x 1 x -20 x 2.5
= (-50) x (-50) = 2500
R.H.S. = 160 x = 160 (2.5)³ x (1)⁷
= 160 x 15.625 x 1 =2500
∴ L.H.S. = R.H.S.

Question 23.
Evaluate : (3.2x⁶y³) x (2.1x²y²) when x = 1 and y = 0.5.
Solution:
3.2x⁶y³ x 2.1x²y²
= 3.2 x 2.1 x x⁶⁺² x y³⁺²
= 6.72x⁸y⁵ = 6.72 x (1)⁸ x (0.5)⁵
= 6.72 x 1 x 0.03125
= 0.21

Question 24.
Find the value of (5x⁶) x (-1.5x²y³) x (-12xy²) when x = 1, y = 0.5.
Solution:

Question 25.
Evaluate : (2.3a⁵b²) x (1.2a²b²) when a = 1, b = 0.5.
Solution:

Question 26.
Evaluate : (-8x²y⁶) x (-20xy) for x = 2.5 and y = 1.
Solution:

Express each of the following products as a monomials and verify the result for x = 1,y = 2: (27-31)

Question 27.
(-xy³) x (yx³) x (xy)
Solution:
(-xy³) x (yx³) x (xy)
= -x x x³ x x x y³ x y x y = -x^{1 + 3 + 1} x y^{3 + 1 + 1} = -x⁵y⁵
Verification:
L.H.S. = (-xy³) x (yx³) x (xy)
= (-1 x 2³) x [2 x (1)³] x (1 X 2)
= (-1 x 8) x (2 x 1) x (1 x 2)
= -8 x 2 x 2 = -32
R.H.S. =-x⁵y⁵  = -(1)⁵ (2)⁵
= -1 x 32 =-32
∴ L.H.S. = R.H.S.

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.

Solution:

Question 32.

Solution:

Question 33.

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.4
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5

Making use of the cube root table, find the cubes root of the following (correct to three decimal places) 
Question 1.
7
Solution:
\(\sqrt [ 3 ]{ 7 }\) =1.913 (From the table)

Question 2.
70
Solution:
\(\sqrt [ 3 ]{ 70 }\) =4.121 (From the table)

Question 3.
700
Solution:
\(\sqrt [ 3 ]{ 700 } =\sqrt [ 3 ]{ 7\times 100 } \)= 8.879 (from \(\sqrt [ 3 ]{ 10x }\))

Question 4.
7000
Solution:
\(\sqrt [ 3 ]{ 7000 } =\sqrt [ 3 ]{ 70\times 100 }\) = 19.13 (from \(\sqrt [ 3 ]{ 100x }\))

Question 5.
1100
Solution:
\(\sqrt [ 3 ]{ 1100 } =\sqrt [ 3 ]{ 11\times 100 }\) = 10.32 (from \(\sqrt [ 3 ]{ 100x }\))

Question 6.
780
Solution:
\(\sqrt [ 3 ]{ 780 } =\sqrt [ 3 ]{ 78\times 100 }\) = 9.205 (from \(\sqrt [ 3 ]{ 10x }\))

Question 7.
7800
Solution:
\(\sqrt [ 3 ]{ 7800 } =\sqrt [ 3 ]{ 78\times 100 }\) = 19.83 (from \(\sqrt [ 3 ]{ 100x }\))

Question 8.
1346
Solution:

Question 9.
250
Solution:

Question 10.
5112
Solution:

Question 11.
9800
Solution:

Question 12.
732
Solution:

Question 13.
7342
Solution:

Question 14.
133100
Solution:

Question 15.
37800
Solution:

Question 16.
0.27
Solution:

Question 17.
8.6
Solution:

Question 18.
0.86
Solution:

Question 19.
8.65
Solution:

Question 20.
7532
Solution:

Question 21.
833
Solution:

Question 22.
34.2
Solution:

Question 23.
What is the length of the side of a cube whose volume is 275 cm³. Make use of the table for the cube root.
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 11 Time and Work Ex 11.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 11 Time and Work Ex 11.1

Question 1.
Rakesh can do a piece of work in 20 days. How much work can he do in 4 days ?
Solution:
Rakesh can do it in 20 days = 1
his 1 day’s work = \(\frac { 1 }{ 20 }\)
and his 4 days work = \(\frac { 1 }{ 20 }\) x 4 = \(\frac { 1 }{ 5 }\) th work

Question 2.
Rohan can paint \(\frac { 1 }{ 3 }\) of a painting in 6 days. How many days will he take to complete the painting ?
Solution:
Rohan can paint \(\frac { 1 }{ 3 }\) of painting in = 6 days
he will complete the painting in = \(\frac { 6 x 3 }{ 1 }\) = 18 days

Question 3.
Anil can do a piece of work in 5 days and Ankur in 4 days. How long will they take to do the same work, if they work together ?
Solution:
Anil’s 1 day’s work = \(\frac { 1 }{ 5 }\)

Question 4.
Mohan takes 9 hours to mow a large lawn. He and Sohan together can mow it in 4 hours. How long will Sohan take to mow the lawn if he works alone ?
Solution:

Question 5.
Sita can finish typing a 100 page document in 9 hours, Mita in 6 hours and Rita in 12 hours. How long will they take to type a 100 page document if they work together?
Solution:
Sita can do a work in 1 hour = \(\frac { 1 }{ 9 }\)

Question 6.
A, B and C working together can do a piece of work in 8 hours. A alone can do it in 20 hours and B alone can do it in 24 hours. In how many hours will C alone do the same work ?
Solution:

Question 7.
A and B can do a piece of work in 18 days; B and C in 24 days and A and C in 36 days. In what time can they do it, all working together ?
Solution:

Question 8.
A and B can do a piece of work in 12 days; B and C in 15 days; C and A in 20 days. How much time will A alone take to finish the work ?
Solution:

Question 9.
A, B and C can reap a field in 15\(\frac { 3 }{ 4 }\) days; B, C and D in 14 days; C, D and A in 18 days; D, A and B in 21 days. In what time can A, B, C and D together reap it ?
Solution:

Question 10.
A and B can polish the floors of a building in 10 days A alone can do \(\frac { 1 }{ 4 }\) th of it in 12 days. In how many days can B alone polish the floor ?
Solution:

Question 11.
A and B can finish a work in 20 days. A alone can do \(\frac { 1 }{ 5 }\) th of the work in 12 days. In how many days can B alone do it ?
Solution:

Question 12.
A and B can do a piece of work in 20 days and B in 15 days. They work together for 2 days and then A goes away. In how many days will B finish the remaining work ?
Solution:

Question 13.
A can do a piece of work in 40 days and B in 45 days. They work together for 10 days and then B goes away. In how many days will A finish the remaining work ?
Solution:

Question 14.
Aasheesh can paint his doll in 20 minutes and his sister Chinki can do so in 25 minutes. They paint the doll together for five minutes. At this juncture they have a quarrel and Chinki withdraws from painting. In how many minutes will Aasheesh finish the painting of the remaining doll ?
Solution:

Question 15.
A and B can do a piece of work in 6 days and 4 days respectively. A started the work; worked at it for 2 days and then was joined by B. Find the total time taken to complete the work.
Solution:

Question 16.
6 men can complete the electric fitting in a building in 7 days. How many days will it take if 21 men do the job ?
Solution:
6 men can complete the work in = 7 days
1 man will complete the same work in = 7 x 6 days (Less men, more days)
21 men will finish the work in = \(\frac { 7 x 6 }{ 21 }\) days (More men, less days) = 2 days

Question 17.
8 men can do a piece of work in 9 days. In how many days will 6 men do it ?
Solution:
8 men can do a work in = 9 days
1 men will do the work in = 9 x 8 days (Less men, more days)
6 men will do the work in = \(\frac { 9 x 8 }{ 6 }\) days (More men, less days)
= \(\frac { 72 }{ 6 }\) = 12 days

Question 18.
Reema weaves 35 baskets in 25 days. In how many days will she weave 55 baskets?
Solution:
Reema can weave 35 baskets in = 25 days

Question 19.
Neha types 75 pages in 14 hours. How many pages will she type in 20 hours ?
Solution:
Neha types pages in 14 hours = 75 pages

Question 20.
If 12 boys earn Rs. 840 in 7 days, what will 15 boys earn in 6 days ?
Solution:
12 boys in 7 days earn an amount of = Rs. 840

Question 21.
If 25 men earn Rs. 1000 in 10 days, how much will 15 men earn in 15 days ?
Solution:
25 men can earn in 10 days = Rs. 1000

Question 22.
Working 8 hours a day, Ashu can copy a book in 18 days. How many hours a day should he work so as to finish the work in 12 days ?
Solution:
Ashu can copy a book in 18 days working in a day = 8 hours
He will copy the book in 1 day working = 8 x 18 hours a day (Less days, more hours a day)
He will copy the book in 12 days working in a day = \(\frac { 8 x 18 }{ 12 }\) hours
(More days, less hours a day)
= \(\frac { 144 }{ 12 }\) = 12 hours a day

Question 23.
If 9 girls can prepare 135 garlands in 3 hours, how many girls are needed to prepare 270 garlands in 1 hour.
Solution:
135 garlands in 3 hours are prepared by = 9 girls
1 garland in 3 hours will be prepared by

Question 24.
A cistern can be filled by one tap in 8 hours, and by another in 4 hours. How long will it take to fill the cistern if both taps are opened together ?
Solution:
First tap’s 1 hour work to fill the cistern = \(\frac { 1 }{ 8 }\)

Question 25.
Two taps A and B can fill an overhead tank in 10 hours and 15 hours respectively. Both the taps are opened for 4 hours and then B is turned off. How much time will A take to fill the remaining tank ?
Solution:

Question 26.
A pipe can fill a cistern in 10 hours. Due to a leak in the bottom, it is filled in 12 hours. When the cistern is full, in how much time will it be emptied by the leak?
Solution:

Question 27.
A cistern has two inlets A and B which can fill it in 12 hours and 15 hours respectively. An outlet can empty the full cistern in 10 hours. If all the three pipes are opened together in the empty cistern, how much time will they take to fill the cistern completely ?
Solution:

Question 28.
A cistern can be filled by a tap in 4 hours and emptied by an outlet pipe in 6 hours. How long will it take to fill the cistern of both the tap and the pipe are opened together ?
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 11 Time and Work Ex 11.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
On what sum will the compound interest at 5% p.a. annum for 2 years compounded annually be Rs 164 ?
Solution:
Let Principal (P) = Rs 100
Rate (R) = 5% p.a.
Period (n) = 2 years

Question 2.
Find the principal of the interest compounded annually at the rate of 10% for two years is Rs 210.
Solution:
Let principal (P) = Rs 100
Rate (R) = 10% p.a.
Period (n) = 2 years

Question 3.
A sum amounts to Rs 756.25 at 10% per annum in 2 years, compounded annually. Find the sum.
Solution:
Amount (A) = Rs 756.25
Rate (R) = 10% p.a.
Period (n) = 2 years

Question 4.
What sum will amount to Rs 4913 in 18 months, if the rate of interest is 12\(\frac { 1 }{ 2 }\) % per annum, compounded half-yearly.
Solution:
Amount (A) = Rs 4,913

Question 5.
The difference between the compound interest and simple interest on a certain sum at 15% per annum for 3 years is Rs 283.50. Find the sum.
Solution:
Let sum (P) = Rs 100
Rate (R) = 15% p.a.
Period (n) = 3 years

Question 6.
Rachna borrowed a certain sum at the rate of 15% per annum. If she paid at the end of two years Rs 1,290 as interest compounded annually, find the sum she borrowed.
Solution:
C.I. = Rs 1,290
Rate (R) = 15% p.a.
Period (n) = 2 years
Let sum (P) = Rs 100

Question 7.
The interest on a sum of Rs 2,000 is being compounded annually at the rate of 4% per annum. Find the period for which the compound interest is Rs 163.20.
Solution:
Sum (P) = Rs 2,000
C.I. = Rs 163.20
Amount (A) = P + C.I. = Rs 2000 + Rs 163.20 = Rs 2163.20
Rate (R) = 4%
Let period = n years

Question 8.
In how much time would Rs 5,000 amount to Rs 6,655 at 10% per annum compound interest ?
Solution:
Principal (P) = Rs 5,000
Amount (A) = Rs 6,655
Rate (R) = 10%
Let period = n years.

Question 9.
In what time will Rs 4,400 becomes Rs 4,576 at 8% per annum interest compounded half-yearly ?
Solution:
Principal (P) = Rs 4,400
Amount (A) = Rs 4,576
Rate (R) = 8% or 4% half-yearly
Let period = n half-years

n = 1
Period = 1 half year

Question 10.
The difference between the S.I. and C.I. on a certain sum of money for 2 years at 4% per annum is Rs 20. Find the sum.
Solution:
Difference between C.I. and S.I. = Rs 20
Rate (R) = 4% p.a.
Period (n) = 2 years
Let principal (P) = Rs 100

Question 11.
In what time will Rs 1,000 amount to Rs 1,331 at 10% per annum compound interest.
Solution:
Principal (P) = Rs 1,000
Amount (A) = Rs 1,331
Rate (R) = 10% p.a.
Let period = n year

Question 12.
At what rate percent compound interest per annum will Rs 640 amount to Rs 774.40 in 2 years ?
Solution:
Principal (P) = Rs 640
Amount (A) = Rs 774.40
Period (n) = 2 years.
Let R be the rate of interest p.a.

Question 13.
Find the rate percent per annum if Rs 2000 amount to Rs 2,662 in 1\(\frac { 1 }{ 2 }\) years, interest being compounded half-yearly ?
Solution:
Principal (P) = Rs 2,000
Amount (A) = Rs 2,662

Question 14.
Kamala borrowed from Ratan a certain rate for two years simple interest. She lent this sum at the same rate to Hari for two years compound interest. At the end of two years, she received Rs 210 as compound interest, but paid Rs 200 only as simple interest. Find the sum and the rate of interest.
Solution:
Simple interest = Rs 200
and compound interest = Rs 210.
Period = 2 years

Question 15.
Find the rate percent per annum, if Rs 2,000 amount to Rs 2,315.25, in an year and a half, interest being compounded six monthly.
Solution:
Principal (P) = Rs 2,000
Amount (A) = Rs 2315.25

Question 16.
Find the rate at which a sum of money will double itself in 3 years, if the interest is compounded annually.
Solution:
Let Principal (P) = Rs 100
then Amount (A) = Rs 200
Period (n) = 3 years
Let R be the rate % p.a.

Question 17.
Find the rate at which a sum of money will become four times the original amount in 2 years, if the interest is compounded half- yearly.
Solution:
Let Principal (P) = Rs 100
Then Amount (A) = Rs 400
Period (n) = 2 years or 4 half years
Let R be the rate % half-yearly, then

Rate % = 41.42% half yearly and 82.84% p.a.

Question 18.
A certain sum amounts to Rs 5,832 in 2 years at 8% compounded interest. Find the sum.
Solution:
Amount (A) = Rs 5,832
Let P be the sum
Rate (R) = 8% p.a.
Period (n) = 2 years

Question 19.
The difference between the compound interest and simple interest on a certain sum for 2 years at 7.5% per annum is Rs 360. Find the sum.
Solution:
Let sum (P) = Rs 100

Question 20.
The difference in simple interest and compound interest on a certain sum of money at 6\(\frac { 2 }{ 3 }\) % per annum for 3 years is Rs 46. Determine the sum.
Solution:
Let sum (P) = Rs 100

Question 21.
Ishita invested a sum of Rs 12,000 at 5% per annum compound interest. She received an amount of Rs 13,230 after n years, Find the value of n.
Solution:
Principal (P) = Rs 12,000
Amount (A) = Rs 13,230
Rate (R) = 5% p.a.
Period = n years

Question 22.
At what rate percent per annum will a sum of Rs 4,000 yield compound interest of Rs 410 in 2 years ?
Solution:
Principal (P) = Rs 4,060
C.I. = Rs 410
Amount (A) = Rs 4,000 + 410 = Rs 4,410
Let rate = R % p.a.
Period (n) = 2 years

Question 23.
A sum of money deposited at 2% per annum compounded annually becomes Rs 10404 at the end of 2 years. Find the sum deposited.
Solution:
Amount (A) = Rs 10,404
Rate (R) = 2% p.a.
Period (n) = 2 years.

Question 24.
In how much time will a sum of Rs 1,600 amount to Rs 1852.20 at 5% per annum compound interest ?
Solution:
Principal (P) = Rs 1,600
Amount (A) = Rs 1852.20
Rate (R) = 5% p.a.
Let n be the time

Question 25.
At what rate percent will a sum of Rs 1,000 amount to Rs 1102.50 in 2 years at compound interest ?
Solution:
Principal (P) = Rs 1,000
Amount (A) = Rs 1102.50 .
Period (n) = 2 years
Let R be the rate of interest p.a.

Question 26.
The compound interest on Rs 1,800 at 10% per annum for a certain period of time is Rs 378. Find the time in years.
Solution:
Principal (P) = Rs 1,800
C.I. = Rs 378
Amount (A) = P + C.I. = Rs 1,800 + 378 = Rs 2,178
Rate (R) = 10% p.a.
Let n be the period in years

Comparing, we get:
n = 2
Period = 2 years

Question 27.
What sum of money will amount to Rs 45582.25 at 6\(\frac { 3 }{ 4 }\) % per annum in two years, interest being compounded annually ?
Solution:
Amount (A) = Rs 45582.25

Question 28.
Sum of money amounts to Rs 4,53,690 in 2 years at 6.5% per annum compounded annually. Find the sum.
Solution:
Amount (A) = Rs 4,53,690

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
Compute the amount and the compound interest in each of the following by using the formula when :
(i) Principal = Rs 3,000, Rate = 5%, Time = 2 years
(ii) Principal = Rs 3,000 Rate = 18%, Time = 2 years
(iii) Principal = Rs 5,000 Rate = 10 paise per rupee per annum, Time = 2 years
(iv) Principal = Rs 2,000, Rate = 4 paise per rupee per annum, Time = 3 years.
(v) Principal = Rs 12,800, Rate = 7\(\frac { 1 }{ 2 }\) %, Time = 3 years
(vi) Principal = Rs 10,000, Rate = 20% per annum compounded half-yearly, time = 2 years
(vii) Principal = Rs 1,60,000, Rate = 10 paise per rupee per annum compounded half- yearly, Time = 2 years.
Solution:
(i) Principal (P) = Rs 3,000
Rate (R) = 5% p.a.
Time (n) = 2 years

and compound interest (C.I) = A – P = Rs 3307.50 – Rs 3,000 = Rs 307.50
(ii) Principal (P) = Rs 3,000
Rate (R) = 18% p.a.
Time (n) = 2 years

and compound interest (C.I.) = A – P = Rs 4177.20 – Rs 3,000 = Rs 1177.20
(iii) Principal (P) = Rs 5,000
Rate (R) =10 paise per rupee or 10% p.a.
Time (n) = 2 years.

C.I. = A – P = Rs 6,050 – Rs 5,000 = Rs 1,050
(iv) Principal (P) = Rs 2,000
Rate (R) = 4 paise per rupee or 4% p.a.
Time (n) = 3 years

C.I. = A – P = Rs 2249.73 – Rs 2,000 = Rs 249.73
(v) Principal (P) = Rs 12,800

C.I. = A – P = Rs 15901.40 – Rs 12,800 = Rs 3101.40
(vi) Principal (P) = Rs 10,000
Rate (R) = 20% p.a. or 10% half-yearly
Time = 2 years or 4 half-years

C.I. = A – P = Rs 14,641 – Rs 10,000 = Rs 4,641
(vii) Principal (P) = Rs 1,60,000
Rate (R) = 10 paise per rupee or 10% p.a. or 5% half-yearly
Time (n) = 2 years or 4 half-years.

C.I. = A – P = Rs 1,94,481 – Rs 1,60,000 = Rs 34,481

Question 2.
Find the amount of Rs 2,400 after 3 years, when the interest is compounded annually at the rate of 20% per annum.
Solution:
Principal (P) = Rs 2,400
Rate (R) = 20%
Time (n) = 3 years

Question 3.
Rahman lent Rs 16,000 to Rasheed at the rate of 12\(\frac { 1 }{ 2 }\) % per annum compound interest. Find the amount payable by Rasheed to Rahman after 3 years.
Solution:
Principal (P) = Rs 16,000

Question 4.
Meera borrowed a sum of Rs 1,000 from Sita for two years. If the rate of interest is 10% compounded annually find the amount that Meera has to pay back.
Solution:
Amount of loan (P) = Rs 1,000
Rate (R) = 10% p.a.
Period (n) = 2 years

Question 5.
Find the difference between the compound interest and simple interest. On a sum of Rs 50,000 at 10% per annum for 2 years.
Solution:
Principal (P) = Rs 50,000
Rate (R) = 10% p.a.
Period (n) = 2 years.

Difference between C.I. and S.I. = Rs 10,500 – Rs 10,000 = Rs 500

Question 6.
Amit borrowed Rs 16,000 at 17\(\frac { 1 }{ 2 }\) % per annum simple interest on the same day, he lent it to Ashu at the same rate but compounded annually. What does he gain at the end of 2 years ?
Solution:
Amount of loan (P) = Rs 16,000


C.I. = A – P = Rs 22,090 – Rs 16,000 = Rs 6,090
Now gain = C.I. – S.I = Rs 6,090 – 5,600 = Rs 490

Question 7.
Find the amount of Rs 4,096 for 18 months at 12\(\frac { 1 }{ 2 }\) % per annum, interest being compounded semi-annually ?
Solution:
Principal (P) = Rs 4,096

Question 8.
Find the amount and the compound interest on Rs 8,000 for 1\(\frac { 1 }{ 2 }\) years at 10% per annum, compounded half-yearly.
Solution:
Principal (P) = Rs 8,000
Rate (R) = 10% p.a. or 5% half yearly

and C.I. = A – P = Rs 9,261 – Rs 8,000 = Rs 1,261

Question 9.
Kamal borrowed Rs 57,600 from LIC against her policy at 12\(\frac { 1 }{ 2 }\) % per annum to build a house. Find the amount that she pays LIC after 1\(\frac { 1 }{ 2 }\) years if the interest is calculated half-yearly.
Solution:
Amount of loan (P) = Rs 57,600

Question 10.
Abha purchased a house from Avas Parishad on credit. If the cost of the house is Rs 64,000 and the rate of interest is 5% per annum compounded half-yearly, find the interest paid by Abha after one year and a half.
Solution:
Price of house (P) = Rs 64,000

Compound interest (C.I.) = A – P = Rs 68,921 – Rs 64,000 = Rs 4,921

Question 11.
Rakesh lent out Rs 10,000 for 2 years at 20% per annum compounded annually. How much more he could earn if the interest be compounded half-yearly ?
Solution:
Principal (P) = Rs 10,000
Rate (R) = 20% p.a. or 10% half-yearly
Period (n) = 2 years or 4 half-years


C.I. = Rs 14,400 – Rs 10,000 = Rs 4,400
Now difference in C.I. = Rs 4,641 – Rs 4,400 = Rs 241

Question 12.
Romesh borrowed a sum of Rs 2,45,760 at 12.5% per annum compounded annually. On the same day, he lent out his money to Ramu at the same rate of interest but compounded semi-annually. Find his gain after 2 years.
Solution:
In first case,
Principal (P) = Rs 2,45,760


C.I. = A – P = Rs 313203.75 – Rs 2,45,760 = Rs 67443.75
Gain = 67443.75 – Rs 65,280 = Rs2163.75

Question 13.
Find the amount that David would receive if he invests Rs 8,192 for 18 months at 12\(\frac { 1 }{ 2 }\) % per annum, the interest being compounded half-yearly.
Solution:
Principal (P) = Rs 8,192

Question 14.
Find the compound interest on Rs 15,625 for 9 months at 16% per annum, compounded quarterly.
Solution:
Principal (P) = Rs 15,625
Rate (R) = 16% p.a. or 4% quarterly
Period (n) = 9 months or 3 quarters

Compound interest = A – P = Rs 17,576 – Rs 15,625 = Rs 1,951

Question 15.
Rekha deposited Rs 16,000 in a foreign bank which pays interest at the rate of 20% per annum compounded quarterly, find the interest received by Rekha after one year.
Solution:
Principal (P) = Rs 16,000
Rate (R) = 20% p.a. or 5% quarterly
Period (n) = one year or 4 quarters

C.I. = A – P = Rs 19448.10 – Rs 16,000 = Rs 3448.10

Question 16.
Find the amount of Rs 12,500 for 2 years compounded annually, the rate of interest being 15% for the first year and 16% for the second year.
Solution:
Principal (P) = Rs 12,500
Rate (R1) = 15% p.a. for first year
R2 = 16% p.a. for second year
Period = 2 years

Question 17.
Ramu borrowed Rs 15,625 from a finance company to buy a scooter. If the rate of interest be 16% per annum compounded annually, what payment he will have to make after 2\(\frac { 1 }{ 4 }\) years ?
Solution:
Principal (P) = Rs 15,625
Rate (R) = 16%

Question 18.
What will Rs 1,25,000 amount to at the rate of 6% if interest is calculated after every 4 months for one year ?
Solution:
Principal (P) = Rs 1,25,000

Question 19.
Find the compound interest at the rate of 5% for 3 years on that principal which in 3 years at the rate of 5% per annum gives Rs 12,000 as simple interest.
Solution:
In first case,
S.I. = Rs 12,000
Rate (R) = 5% p.a.
Period (T) = 3 years

= Rs 80,000
In second case,
Principal (P) = Rs 80,000
Rate (R) = 5% p.a.
Period (n) = 3 years

C.I. = A – P = Rs 92,610 – 80,000 = Rs 12,610

Question 20.
A sum of money was lent for 2 years at 20% compounded annually. If the interest is payable half-yearly instead of yearly, then the interest is Rs 482 more. Find the sum.
Solution:
Let Sum (P) = Rs x
Rate (R) = 20% p.a. or 10% half-yearly
Period (n) = 2 years or 4 half years
In first case,

Interests = A – P = Rs 146.41 – Rs 100 = Rs 46.41
Now difference in interests = Rs 46.41 – Rs 44.00 = Rs 2.41
If difference is 2.41 then sum is 100 If difference is Rs 482, then sum

Question 21.
Simple interest on a sum of money for 2 years at 6\(\frac { 1 }{ 2 }\) % per annum is Rs 5,200. What will be the compound interest on the sum at the same rate for the same period ?
Solution:
In first case,
S.I. = Rs 5,200


Compound interest = A – P = Rs 45,369 – Rs 40,000 = Rs 5,369

Question 22.
Find the compound interest at the rate of 5% per annum for 3 years on that principal which in 3 years at the rate of 5% per annum gives Rs 1,200 as simple interest.
Solution:
In first case,
S.I. = Rs 1,200
Rate (R) = 5% p.a.
Period (T) = 3 years

In second case,
Principal (P) = Rs 8,000
Rate (R) = 5% p.a.
Period (n) = 3 years

= Rs 9,261
C.I. = A – P = Rs 9,261 – Rs 8000 = Rs 1,261

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Question 1.
Add the following algebraic expressions


Solution:

Question 2.
Subtract:
(i) -5xy from 12xy
(ii) 2a² from -7a²

Solution:

Question 3.
Take away :


Solution:

Question 4.
Subtract 3x – 4y – 7z from the sum of x – 3y + 2z and – 4X + 9y- 11z.
Solution:
Sum of x – 3y + 2z and – 4x + 9y – 11z
= x – 3y + 2z + (- 4x + 9y – 11z)
= x – 3y + 2z – 4x + 9y – 11z
= x – 4x – 3y + 9y + 2z – 11z
= – 3x + 6y – 9z
Now (-3x + 6y – 9z) – (3x – 4y – 7z)
= -3x + 6y – 9z – 3x + 4y + 7z
= -3x – 3x + 6y + 4y -9z +7z
= -6x + 10y – 2z

Question 5.
Subtract the sum of 3l- 4m – 7n² and 2l + 3m – 4n² from the sum of 9l + 2m – 3n² and -3l + m + 4n².
Solution:
Sum of 9l + 2m – 3n² and -3l + m + 4n²
= 9l + 2m – 3 n² + (-3l) + m + 4n²
= 9l + 2m – 3n² – 3l + m + 4n²
= 9l- 3l+ 2m + m – 3 n² + 4n²
= 6l + 3m + n²
and sum of 3l – 4m – 7n² and 2l +3m- 4n²
= 3l- 4m – 7n² + 2l+ 3m- 4n²
= 3l + 2l – 4m + 3m- 7n² – 4n²
= 5l -m- 11n²
Now (6l + 3m + n²) – (5l – m – 11n²)
= 6l + 3m + n² – 5l + m + 11n²
= 6l – 5l + 3m + m + n² + 11n²
= l + 4m+ 12n²

Question 6.
Subtract the sum of 2x – x² + 5 and -4x – 3 + 7x² from 5.
Solution:
5 – (2x-x² + 5-4x-3 + 7x²)
= 5 – (2x – 4x- x² + 7x² + 5-3)
= 5 – (-2x + 6x² + 2)
= 5 + 2x – 6x² – 2
= – 6x²+2x+3
= 3 + 2x – 6x²

Question 7.

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
• RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5

Question 1.
Find the compound interest when principal = Rs 3,000, rate = 5% per annum and time = 2 years.
Solution:
Principal (P) = Rs 3,000
Rate (R) = 5% p.a.
Period (T) = 2 years

Amount after one year = Rs 3,000 + Rs 150 = 3,150
and principal for the second year = Rs 3,150
and interest for the second year

Compound interest for two years = Rs 150 + Rs 157.50 = Rs 307.50

Question 2.
What will be the compound interest on Rs 4,000 in two years when rate of interest is 5% per annum ?
Solution:
Principal (P) = Rs 4,000
Rate (R) = 5% p.a.
Period (T) = 2 years

Amount after one year = Rs 4,000 + Rs 200 = Rs 4,200
Principal for the second year = Rs 4,200
Interest for the second year

Compound interest for 2 years = Rs 200 + Rs 210 = Rs 410

Question 3.
Rohit deposited Rs 8,000 with a finance company for 3 years at an interest of 15% per annum. What is the compound interest that Rohit gets after 3 years ?
Solution:
Principal (P) = Rs 8,000
Rate (R) = 15% p.a.
Period (T) = 3 years

Amount after first year = Rs 8,000 + RS 1,200 = Rs 9,200
or Principal for the second year = Rs 9,200
Interest for the second year

Amount after 2 years = Rs 9,200 + Rs 1,380 = Rs 10,580
or Principal for the third year = Rs 10,580
Interest for the third year

Compound for the 3 years = Rs 1,200 + Rs 1,380 + Rs 1,587 = Rs 4,167

Question 4.
Find the compound interest on Rs 1,000 at the rate of 8% per annum for 1\(\frac { 1 }{ 2 }\) years when interest is compounded half-yearly ?
Solution:
Principal (P) = Rs 1,000
Rate (R) = 8% p.a.
Period (T) = 1\(\frac { 1 }{ 2 }\) years = 3 half-years

Amount after one half-year = Rs 1,000 + Rs 40 = 1,040
Or principal for the second half-year = Rs 1,040
Interest for the second half-year

Amount after second half-year = Rs 1,040 + 41.60 = Rs 1,081.60
Or principal for the third half-year = Rs 1081.60
Interest for the third half-year

Compound interest for the third half-years or 1\(\frac { 1 }{ 2 }\) years
= Rs 40 + Rs 41.60 + Rs 43.264 = Rs 124.864

Question 5.
Find the compound interest on Rs 1,60,000 for one year at the rate of 20% per annum, if the interest is compounded quarterly.
Solution:
Principal (P) = Rs 1,60,000
Rate (R) = 20% p.a. or 5% quarterly
Period (T) = 1 year or 4 quarters

Amount after first quarter = Rs 1,60,000 + 8,000 = 1,68,000
Or principal for the second quarter = Rs 1,68,000
Interest for the second quarter

Amount after the second quarter = Rs 1,68,000 + Rs 8,400 = 1,76,400
Or principal for the third quarter = Rs 1,76,400
Interest for the third quarter

Amount after third quarter = Rs 1,76,400 + 8,820 = Rs 1,85,220
or Principal for the fourth quarter = Rs. 1,85,220
Interest for the fourth quarter

Total compound interest for the 4 quarters = Rs 8,000 + Rs 8,400 + Rs 8,820 + 9,261 = Rs 34,481

Question 6.
Swati took a loan of Rs 16,000 against her insurance policy at the rate of 12\(\frac { 1 }{ 2 }\) % per annum. Calculate the total compound interest payable by Swati after 3 years.
Solution:
Amount of loan or principal (P) = Rs 16,000

Amount after first year = Rs 16,000 + Rs 2,000 = Rs 18,000
Principal for the second year = Rs 18,000
Interest for the second year

Amount after second year = Rs 18,000 + 2,250 = Rs 20,250
Principal for the third year = Rs 20,250

Compound for 3 years = Rs 2,000 + Rs 2,250 + 2531.25 = Rs 6,781.25

Question 7.
Roma borrowed Rs 64,000 from a bank for 1\(\frac { 1 }{ 2 }\) years at the rate of 10% per annum. Compute the total compound interest payable by Roma after 1\(\frac { 1 }{ 2 }\) years, if the interest is compounded half-yearly.
Solution:
Principal (sum borrowed) (P) = Rs 64,000
Rate (R) = 10% p.a. or 5% half-yearly
Period (T) = 1\(\frac { 1 }{ 2 }\) years or 3 half-years

Amount after first half-year = Rs 64,000 + Rs 3,200 = Rs 67,200
Or principal for the second half-year = Rs 67,200
Interest for the second half-year

Amount after second half-year = Rs 6,7200 + 3,360 = Rs 70,560
Or principal for the third half-year = Rs 70,560
Interest for the third half-year

Total compound interest for 3 half-years
or 1\(\frac { 1 }{ 2 }\) years = Rs 3,200 + Rs 3,360 + Rs 3,528 = Rs 10,088

Question 8.
Mewa Lai borrowed Rs 20,000 from his friend RoopLal at 18% per annum simple interest. He lent it to Rampal at the same rate but compounded annually. Find his gain after 2 years.
Solution:
Principal (P) = Rs 20,000
Rate (R) = 18% p.a.
Period (T) = 2 years

In second case
Interest for the first year

Amount after one year = Rs 20,000 + Rs 3,600 = Rs 23,600
Or principal for the second year = Rs 23,600
Interest for the second year

Interest for two years = Rs 3,600 + 4,248 = Rs 7,848
Gain = Rs 7,848 – Rs 7,200 = Rs 648

Question 9.
Find the compound interest on Rs 8,000 for 9 months at 20% per annum compounded quarterly.
Solution:
Principal (P) = Rs 8,000
Rate (R) = 20% p.a. or 5% p.a. quarterly
Period (T) = 9 months or 3 quarters
Interest for the first quarterly

Amount after first quarter = Rs 8,000 + Rs 400 = Rs 8,400
Or principal for second quarter = Rs 8,400
Interest for the second quarter

Amount after second quarter = Rs 8,400 + Rs 420 = Rs 8,820
Or principal for the third quarter = Rs 8,820
Interest for the third quarter

Compound interest for 9 months or 3 quarters = Rs 400 + Rs 420 + Rs 441 = Rs 1,261

Question 10.
Find the compound interest at the rate of 10% per annum for two years on that principal which in two years at the rate of 10% per annum gives Rs. 200 as simple interest.
Solution:
Simple interest = Rs 200
Rate (R) = 10% p.a.
Period (T) = 2 years.

Now in second case,
Principal CP) = Rs 1,000
Rate (R) = 10% p.a.
Period (T) = 2 years.

Amount after one year = Rs 1,000+ Rs 100 = Rs 1,100
Or principal for the second year = Rs 1,100

Total interest for two years = Rs 100 + Rs 110 = Rs 210

Question 11.
Find the compound interest on Rs 64,000 for 1 year at the rate of 10% per annum compounded quarterly.
Solution:
Principal (P) = Rs 64,000
Rate (R) = 10% p.a. or \(\frac { 5 }{ 2 }\) % quarterly
Period (T) = 1 year = 4 quarters

Amount after first quarter = Rs 64,000 + Rs 1,600 = Rs 65,600
Or principal for the second quarter = Rs 65,600
Interest for the second quarter

Amount after second quarter = Rs 65,600 + Rs 1,640 = Rs 67,240
Or principal for the third year = Rs 67,240

= Rs 1,681
Amount after third quarter = Rs 67,240 + Rs 1,681 = Rs 68,921
Or principal for the fourth quarter

Total compound interest for 4 quarters or one year
= Rs 1,600 + Rs 1,640 + Rs 1,681 + Rs 1723.025 = Rs 6644.025

Question 12.
Ramesh deposited Rs 7,500 in a bank which pays him 12% interest per annum compounded quarterly. What is the amount which he receives after 9 months ?
Solution:
Principal (P) = Rs 7,500
Rate (R) = 12% p.a. or 3% quarterly
Time (T) = 9 months or 3 quarters

Amount after one quarter = Rs 7,500 + Rs 225 = Rs 7,725
Or Principal for second quarter = Rs 7,725
Interest for the second quarter

Amount after second quarter = Rs 7,725 + Rs 231.75 = Rs 7956.75
Or principal for the third quarter

Total amount he received after 9 months = Rs 7956.75 + Rs 238.70 = Rs 8195.45

Question 13.
Anil borrowed a sum of Rs 9,600 to install a hand pump in his dairy. If the rate of interest is 5\(\frac { 1 }{ 2 }\) % .per annum compounded annually, determine the compound interest which Anil will have to pay after 3 years.
Solution:
Principal (P) = Rs 9,600
Rate of interest (R) = 5\(\frac { 1 }{ 2 }\) % = \(\frac { 11 }{ 2 }\) % p.a.
Period (T) = 3 years.

Amount after one year = Rs 9,600 + Rs 528 = Rs 10,128
Or principal for second year = Rs 10,128
Interest for the second year

Amount after second year = Rs 10,128 + Rs 557.04 = Rs 10685.04
or Principal for the third year = Rs 10685.04
Interest for the third year

Total compound interest = Rs 528 + Rs 557.04 + Rs 587.68 = Rs 1672.72

Question 14.
Surabhi borrowed a sum of Rs 12,000 from a finance company to purchase a refrigerator. If the rate of interest is 5% per annum compounded annually, calculate the compound interest that Surabhi has to pay to the company after 3 years.
Solution:
Sum of money borrowed (P) = Rs 12,000
Rate (R) = 5% p.a.
Period (T) = 3 years

Amount after one year = Rs 12,000 + Rs 600 = Rs 12,600
Or principal for the second year = Rs 12,600
Interest for the second year

Amount after second year = Rs 12,600 + Rs 630 = Rs 13,230
Or Principal for the third year = Rs 13,230
Interest for the third year

Total compound interest for 3 years = Rs 600 + Rs 630 + Rs 661.50 = Rs 1891.50

Question 15.
Daljit received a sum of Rs 40,000 as a loan from a finance company. If the rate of interest is 7% per annum compounded annually, calculate the compound interest that Daljit pays after 2 years.
Solution:
Amount of loan (P) = Rs 40,000
Rate (R) = 7% p.a.
Period = 2 years

Amount after one year = Rs 40,000 + Rs 2,800 = Rs 42,800
Or principal for the second year = Rs 42,800
Interest for the second year

Total interest paid after two years = Rs 2,800 + 2,996 = Rs 5,796

Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.