RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
Other Exercises
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.4
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5
Question 1.
Find the cubes of the following numbers:
(i) 7
(ii) 12
(iii) 16
(iv) 21
(v) 40
(vi) 55
(vii) 100
(viii) 302
(ix) 301
Solution:
(i) (7)3 = 7 x 7 x 7 = 343
(ii) (12)3 = 12 x-12 x 12 = 1728
(iii) (16)3 = 16 x 16 x 16 = 4096
(iv) (21)3 = 21 x 21 x 21 = 441 x 21 =9261
(v) (40)3 = 40 x 40 x 40 = 64000
(vi) (55)3 = 55 x 55 x 55 = 3025 x 55 = 166375
(vii) (100)3 = 100 x 100 x 100 =1000000
(viii)(302)3 = 302 x 302 x 302 = 91204 x 302 = 27543608
(ix) (301)3 = 301 x 301 x 301 = 90601 x 301 =27270901
Question 2.
Write the cubes of all natural numbers between 1 and 10 and verify the following statements :
(i) Cubes of all odd natural numbers are odd.
(ii) Cubes of all even natural numbers are even.
Solution:
Cubes of first 10 natural numbers :
(1)3 = 1 x 1 x 1 = 1
(2)3 = 2 x 2 x 2 = 8
(3)3 = 3 x 3 x 3 = 27
(4)3= 4 x 4 x 4 = 64
(5)3 = 5 x 5 x 5 = 125
(6)3 = 6 x 6 x 6 = 216
(7)3 = 7 x 7 x 7 = 343
(8)3 = 8 x 8 x 8 = 512
(9)3 = 9 x 9 x 9= 729
(10)3 = 10 x 10 x 10= 1000
We see that the cubes of odd numbers is also odd and cubes of even numbers is also even.
Question 3.
Observe the following pattern :
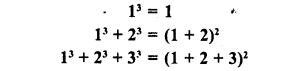
Write the next three rows and calculate the value of 13 + 23 + 33 +…. + 93 + 103 by the above pattern.
Solution:
We see the pattern
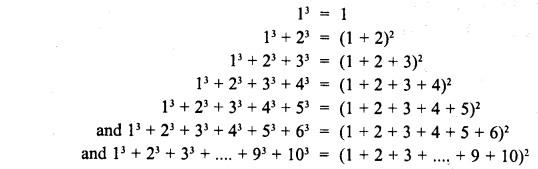
Question 4.
Write the cubes of 5 natural numbers which are multiples of 3 and verify the followings :
The cube of a natural number which is a multiple of 3 is a multiple of 27′
Solution:
5 natural numbers which are multiples of 3
3,6,9,12,15.
(3)3 = 3 x 3 x 3 = 27
Which is multiple of 27
(6)3 = 6 x 6 x 6 = 216 ÷ 27 = 8
Which is multiple of 27
(9)3 = 9 x 9 x 9 = 729 + 27 = 27
Which is multiple of 27
(12)3= 12 x 12 x 12 = 1728 ÷ 27 = 64
Which is multiple of 27
(15)3 = 15 x 15 x 15 = 3375 ÷ 27 = 125
Which is multiple of 27
Hence, cube of multiple of 3 is a multiple of 27
Question 5.
Write the cubes of 5 natural numbers which are of the form 3n+ 1 (e.g.,4, 7, 10, …………) and verify the following :
‘The cube of a natural number of the form 3n + 1 is a natural number of the same form i.e. when divided by 3 it leaves the remainder 1’.
Solution:
3n + 1
Let n = 1, 2, 3, 4, 5, then
If n = 1, then 3n +1= 3 x 1+1= 3+1= 4
If n = 2, then 3n +1=3 x 2+1=6+1=7
If n = 3, then 3n + 1= 3 x 3 + 1= 9 + 1 = 10
If n = 4, then 3n + 1= 3 x 4+1 = 12 + 1= 13
If n = 5, then 3n +1=3 x 5 + 1 = 15 +1 = 16
Now
(4)3 = 4 x 4 x 4 = 64
Which is \(\frac {64 }{ 3 }\)=21, Remainder = 1
(7)3 = 7 x 7 x 7 = 343
Which is \(\frac {343 }{ 3 }\) =114, Remainder = 1
(10)3 = 10 x 10 x 10 = 1000 ÷ 3 = 333, Remainder = 1
(13)3 = 13 x 13 x 13 = 2197 ÷ 3 = 732, Remainder = 1
(16)3 = 16 x 16 x 16 = 4096 ÷ 3 = 1365, Remainder = 1
Hence cube of natural number of the form, 3n + 1, is a natural of the form 3n + 1
Question 6.
Write the cubes of 5 natural numbers of the form 3n + 2 (i.e. 5, 8, 11,……… ) and verify the following :
‘The cube of a natural number of the form 3n + 2 is a natural number of the same form i.e. when it is dividend by 3 the remainder is 2’.
Solution:
Natural numbers of the form 3n + 2, when n
is a natural number i.e. 1, 2, 3, 4, 5,………….
If n = 1, then 3n + 2 = 3 x 1+2 = 3+ 2 = 5
If n = 2, then 3n + 2 = 3 x 2 + 2 = 6 + 2 = 8
If n = 3, then 3n + 2 = 3 x 3 + 2 = 9 + 2 = 11
If n = 4, then 3n + 2 = 3 x 4 + 2 = 12 + 2 = 14
and if n = 5, then 3n + 2 = 3 x 5 + 2 = 15 + 2= 17
Now (5)3 = 5 x 5 x 5 = 125
125 + 3 = 41, Remainder = 2
(8)2 = 8 x 8 x 8 = 512 512 -s- 3 = 170, Remainder = 2
(11)3 = 11 x 11 x 11 = 1331
1331 + 3 = 443, Remainder = 2
(14)3 = 14 x 14 x 14 = 2744
2744 + 3 = 914, Remainder = 2
(17)3 = 17 x 17 x 17 = 4913
4913 = 3 = 1637, Remainder = 2
We see the cube of the natural number of the
form 3n + 2 is also a natural number of the
form 3n + 2.
Question 7.
Write the cubes of 5 natural numbers of which are multiples of 7 and verify the following :
‘The cube of a multiple of 7 is a multiple of 73′.
Solution:
5 natural numbers which are multiple of 7,are 7, 14, 21, 28, 35
(7)3 = (7)3 which is multiple of 73
(14)3 = (2 x 7)3 = 23 x 73, which is multiple of 73
(21)3 = (3 x 7)3 = 33 x 73, which is multiple of 73
(28)3 = (4 x 7)3 = 43 x 73, which is multiple of 73 (35)3 = (5 x 7)3 = 53 x 73 which is multiple of 73
Hence proved.
Question 8.
Which of the following are perfect cubes?
(i) 64
(ii) 216
(iii) 243
(iv) 1000
(v) 1728
(vi) 3087
(vii) 4608
(viii) 106480
(ix) 166375
(x) 456533
Solution:
(i) 64 = 2 x 2 x 2 x 2 x 2 x 2

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 64 is a perfect cube
(ii) 216 = 2 x 2 x 2 x 3 x 3 x 3
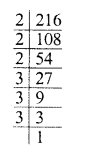
Grouping the factors in triplets of equal factors, we see that no factor is left
216 is a perfect cube.
(iii) 243 = 3 x 3 x 3 x 3 x 3
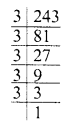
Grouping the factors in triplets, we see that two factors 3 x 3 are left
∴ 243 is not a perfect cube.
(iv) 1000 = 2 x 2 x 2 x 5 x 5 x 5

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 1000 is a perfect cube.
(v) 1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors in triplets of the equal factors, we see that no factor is left
∴ 1728 is a perfect cube,
(vi) 3087 = 3 x 3 x 7 x 7 x 7

Grouping the factors in triplets of the equal factors, we see that two factor 3×3 are left
∴ 3087 is not a perfect cube.
(vii) 4608 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3

Grouping the factors in triplets of equal factors, we see that two factors 3, 3 are left
∴ 4609 is not a perfect cube.
(viii) 106480 = 2 x 2 x 2 x 2 x 5 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, we see that factors 2, 5 are left
∴ 106480 is not a perfect cube.
(ix) 166375 = 5 x 5 x 5 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 166375 is a perfect cube.
(x) 456533 = 7 x 7 x 7 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 456533 is a perfect cube.
Question 9.
Which of the following are cubes of even natural numbers ?
216, 512, 729,1000, 3375, 13824
Solution:
We know that the cube of an even natural number is also an even natural number
∴ 216, 512, 1000, 13824 are even natural numbers.
∴ These can be the cubes of even natural number.
Question 10.
Which of the following are cubes of odd natural numbers ?
125, 343, 1728, 4096, 32768, 6859
Solution:
We know that the cube of an odd natural number is also an odd natural number,
∴ 125, 343, 6859 are the odd natural numbers
∴ These can be the cubes of odd natural numbers.
Question 11.
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes ?
(i) 675
(ii) 1323
(iii) 2560
(iv) 7803
(v) 107311
(vi) 35721
Solution:
(i) 675 = 3 x 3 x 3 x 5 X 5
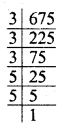
Grouping the factors in triplet of equal factors, 5 x 5 are left without triplet
So, by multiplying by 5, the triplet will be completed.
∴ Least number to be multiplied = 5
(ii) 1323 = 3 x 3 x 3 x 7 x 7

Grouping the factors in triplet of equal factors. We find that 7 x 7 has been left
So, multiplying by 7, we get a triplet
∴ The least number to be multiplied = 7
(iii) 2560 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 5

Grouping the factors in triplet of equal factors, 5 is left.
∴ To complete a triplet 5 x 5 is to multiplied
∴ Least number to be multiplied = 5 x 5 = 25
(iv) 7803 = 3 x 3 x 3 x 17 x 17

Grouping the factors in triplet of equal factors, we find the 17 x 17 are left
So, to complete the triplet, we have to multiply by 17
∴ Least number to be multiplied = 17
(v) 107811 = 3 x 3 x 3 x 3 x 11 x 11 x 11

Grouping the factors in triplet of equal factors, factor 3 is left
So, to complete the triplet 3 x 3 is to be multiplied
∴ Least number to be multiplied = 3 x 3 = 9
(vi) 35721 = 3 x 3 x 3 x 3 x 3 x 3 x 7 x 7

Grouping the factors in triplet of equal factors, we find that 7 x 7 is left
So, in order to complete the triplets, we have to multiplied by 7
∴ Least number to be multiplied = 7
Question 12.
By which smallest number must the following numbers be divided so that the quotient is a perfect cube ?
(i) 675
(ii) 8640
(iii) 1600
(iv) 8788
(v) 7803
(vi) 107811
(vii) 35721
(viii) 243000
Solution:
(i) 675 = 3 x 3 x 3 x 5 x 5
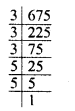
Grouping the factors in triplet of equal factors, 5 x 5 is left
5 x 5 is to be divided so that the quotient will be a perfect cube.
∴ The least number to be divided = 5 x 5 = 25
(ii) 8640 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors in triplets of equal factors, 5 is left
∴ In order to get a perfect cube, 5 is to divided
∴ Least number to be divided = 5
(iii) 1600 = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5

Grouping the factors in triplets of equal factors, we find that 5 x 5 is left
∴ In order to get a perfect cube 5 x 5 = 25 is to be divided.
∴ Least number to be divide = 25
(iv) 8788 = 2 x 2 x 13 x 13 x 13

Grouping the factors in triplets of equal factors, we find that 2 x 2 has been left
∴ In order to get a perfect cube, 2 x 2 is to be divided
∴ Least number to be divided = 4
(v) 7803 = 3 x 3 x 3 x 17 x 17

Grouping the factors in triplets of equal factors, we see that 17 x 17 has been left.
So, in order to get a perfect cube, 17 x 17 is be divided
∴ Least number to be divided = 17 x 17 = 289
(vi) 107811 = 3 x 3 x 3 x 3 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, 3 is left
∴ In order to get a perfect cube, 3 is to be divided
∴ Least number to be divided = 3
(vii) 35721 = 3 x 3 x 3 x 3 x 3 x 3 x 7 x 7

Grouping the factors in triplets of equal factors, we see that 7 x 7 is left
So, in order to get a perfect cube, 7 x 7 = 49 is to be divided
∴ Least number to be divided = 49
(viii) 243000 = 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 5 x 5 x 5

Grouping the factors in triplets of equal factors, 3 x 3 is left
∴ By dividing 3 x 3, we get a perfect cube
∴ Least number to be divided = 3 x 3=9
Question 13.
Prove that if a number is trebled then its cube is 27 times the cube of the given number.
Solution:
Let x be the number, then trebled number of x = 3x
Cubing, we get:
(3x)3 = (3)3 x3 = 27x3
27x3 is 27 times the cube of x i.e., of x3
Question 14.
What happenes to the cube of a number if the number is multiplied by
(i) 3 ?
(ii) 4 ?
(iii) 5 ?
Solution:
number (x)3 = x3
(i) If x is multiplied by 3, then the cube of
∴ (3x)3 = (3)3 x x3 = 27x3
∴ The cube of the resulting number is 27 times of cube of the given number
(ii) If x is multiplied by 4, then the cube of
(4x)3 = (4)3 x x3 = 64x3
∴ The cube of the resulting number is 64 times of the cube of the given number
(ii) If x is multiplied by 5, then the cube of
(5x)3 = (5)3 x x3 = 125x3
∴ The cube of the resulting number is 125 times of the cube of the given number
Question 15.
Find the volume of a cube, one face of which has an area of 64 m2.
Solution:
Area of one face of a cube = 64 m2
∴ Side (edge) of cube = √64
= √64 = 8 m
∴ Volume of the cube = (side)3 = (8 m)3 = 512 m3
Question 16.
Find the volume of a cube whose surface area is 384 m2.
Solution:
Surface area of a cube = 384 m2 Let side = a
Then 6a2 = 384 ⇒ a2 = \(\frac {384 }{ 6 }\)= 64 = (8)2
∴ a = 8 m
Now volume = a3 = (8)3 m3 = 512 m3
Question 17.
Evaluate the following :
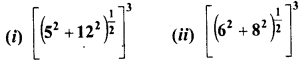
Solution:
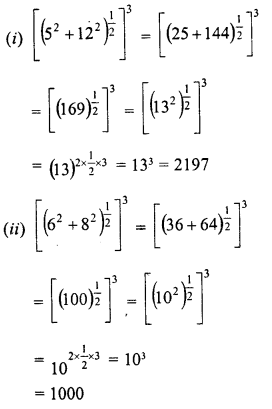
Question 18.
Write the units digit of the cube of each of the following numbers :
31,109,388,833,4276,5922,77774,44447, 125125125.
Solution:
We know that if unit digit of a number n is
= 1, then units digit of its cube = 1
= 2, then units digit of its cube = 8
= 3, then units digit of its cube = 7
= 4, then units digit of its cube = 4
= 5, then units digit of its cube = 5
= 6, then units digit of its cube = 6
= 7, then the units digit of its cube = 3
= 8, then units digit of its cube = 2
= 9, then units digit of its cube = 9
= 0, then units digit of its cube = 0
Now units digit of the cube of 31 = 1
Units digit of the cube of 109 = 9
Units digits of the cube of 388 = 2
Units digits of the cube of 833 = 7
Units digits of the cube of 4276 = 6
Units digit of the cube of 5922 = 8
Units digit of the cube of 77774 = 4
Units digit of tl. cube of 44447 = 3
Units digit of the cube of 125125125 = 5
Question 19.
Find the cubes of the following numbers by column method :
(i) 35
(ii) 56
(iii) 72
Solution:
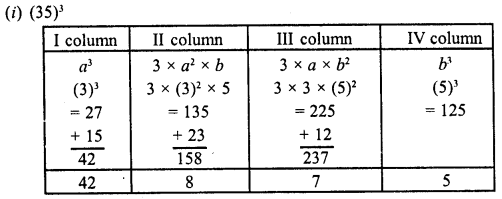
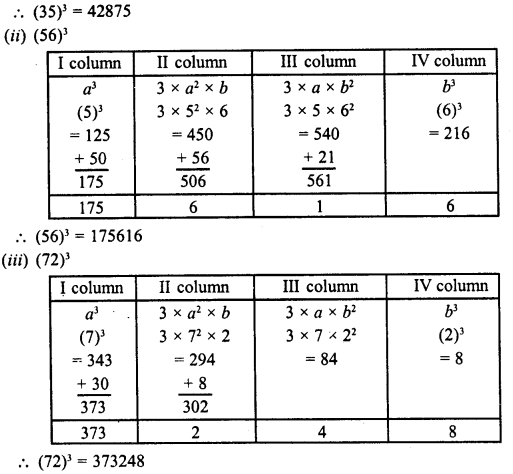
Question 20.
Which of the following numbers are not perfect cubes ?
(i) 64
(ii) 216
(iii) 243
(iv) 1728
Solution:
(i) 64 = 2 x 2 x 2 X 2 x 2 x 2
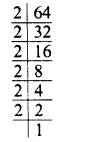
Grouping the factors in triplets, of equal factors, we see that no factor is left
∴ 64 is a perfect cube.
(ii) 216 = 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors in triplets, of equal factors, we see that no factor is left
∴ 216 is a perfect cube.
(iii) 243 = 3 x 3 x 3 x 3 x 3
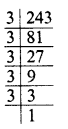
Grouping the factors in triplets, of equal factors, we see that 3 x 3 are left
∴ 243 is not a perfect cube.
(iv) 1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors m triplets, of equal factors, we see that no factor is left.
∴ 1728 is a perfect cube.
Question 21.
For each of the non-perfect cubes, in Q. 20, find the smallest number by which it must be
(a) multiplied so that the product is a perfect cube.
(b) divided so that the quotient is a perfect cube.
Solution:
In qustion 20, 243 is not a perfect cube and 243 = 3 x 3 x 3 x 3 x 3
Grouping the factors in triplets, of equal factors, we see that 3 x 3 is left.
(a) In order to make it a perfect cube, 3 is to be multiplied which makes a triplet.
(b) In order to make it a perfect cube, 3 x 3 or 9 is to be divided.
Question 22.
By taking three different values of n verify the truth of the following statements :
(i) If n is even, then n3 is also even.
(ii) If n is odd, then n3 is also odd.
(iii) If n leaves remainder 1 when divided by 3, then it3 also leaves 1 as remainder when divided by 3.
(iv) If a natural number n is of the form 3p + 2 then n3 also a number of the same type.
Solution:
(i) n is even number.
Let n = 2, 4, 6 then
(a) n3 = (2)3 = 2 x 2 x 2 = 8, which is an even number.
(b) (n)3= (4)3 = 4 x 4 x 4 = 64, which is an even number.
(c) (n)3 = (6)3 = 6 x 6 x 6 = 216, which is an even number.
(ii) n is odd number.
Letx = 3, 5, 7
(a) (n)3 = (3)3 = 3 x 3 x 3 = 27, which is an odd number.
(b) (n)3 = (5)3 = 5 x 5 x 5 = 125, which is an odd number.
(c) (n)3 = (7)3 = 7 x 7 x 7 = 343, which is an odd number.
(iii) If n leaves remainder 1 when divided by 3, then n3 is also leaves 1 as remainder,
Let n = 4, 7, 10 If n = 4,
then «3 = (4)3 = 4 x 4 x 4 = 64
= 64 + 3 = 21, remainder = 1
If n = 7, then
n3 = (7)3 = 7 x 7 x 7 = 343
343 + 3 = 114, remainder = 1
If n – 10, then
(n)3 = (10)3 = 10 x 10 x 10 = 1000
1000 + 3 = 333, remainder = 1
(iv) If the natural number is of the form 3p + 2, then n3 is also of the same type
Let p =’1, 2, 3, then
(a) If p = 1, then
n = 3p + 2 = 3 x 1+2=3+2=5
∴ n3 = (5)3 = 5 x 5 x 5 = 125
125 = 3 x 41 + 2 = 3p +2
(b) If p = 2, then
n = 3p + 2 = 3 x 2 + 2 = 6 + 2 = 8
∴ n3 = (8)3 = 8 x 8 x 8 = 512
∴ 512 = 3 x 170 + 2 = 3p + 2
(c) If p = 3, then
n = 3p + 2 = 3 x 3 + 2 = 9 + 2 = 11
∴ n3 = (11)3 = 11 x 11 x 11 = 1331
and 1331 =3 x 443 + 2 = 3p + 2
Hence proved.
Question 23.
Write true (T) or false (F) for the following statements :
(i) 0 392 is a perfect cube.
(ii) 8640 is not a perfect cube.
(iii) No cube can end with exactly two zeros.
(iv) There is no perfect cube which ends in 4.
(v) For an integer a, a3 is always greater than a2 > b2
(vi) If a and b are integers such that a2 > b2 , then a3 > b3.
(x) If a2 ends in an even number of zeros, then a ends in an odd number of zeros.
Solution:
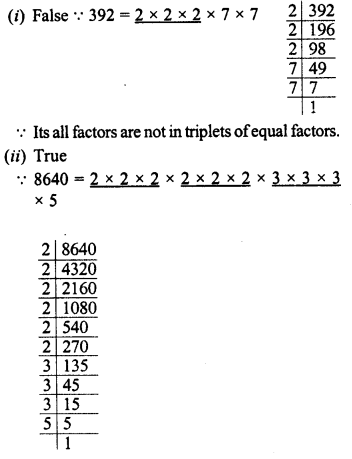
∵ 5 is left.
(iii)True : A number ending three zeros can be a perfect cube.
(iv) False : v (4)3 = 4 x 4 x 4 = 64, which ends with 4.
(v) False : If n is a proper fraction, it is not possible.
(vi) False : It is not true if a and b are proper fraction.
(vii) True.
(viii) False : as a2 ends in 9, then a3 does not necessarily ends in 7. It ends in 3 also.
(ix) False : it is not necessarily that a3 ends in 25 it can end also in 75.
(x) False : If a2 ends with even zeros, then a3 will ends with odd zeros but of multiple of 3.
Hope given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.