Category: CBSE Class 8

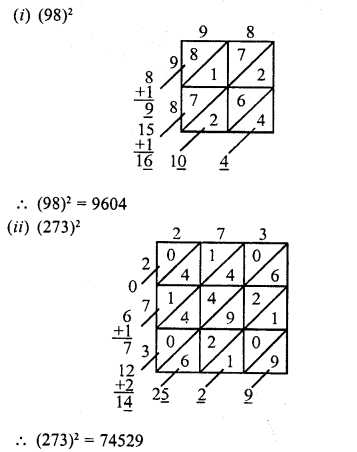
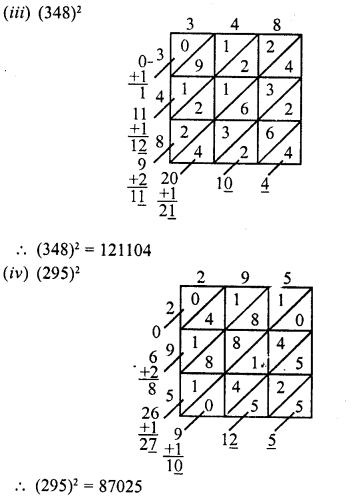
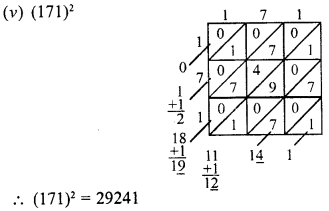
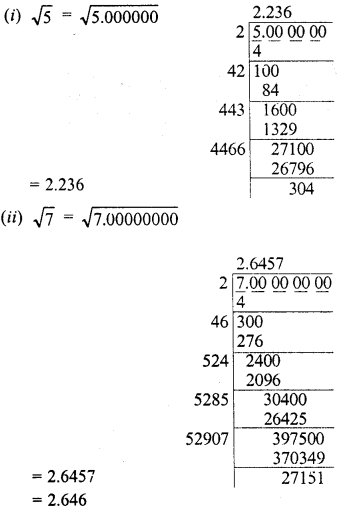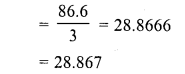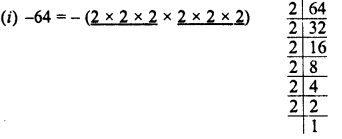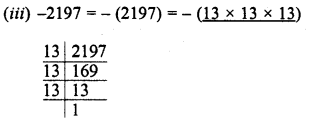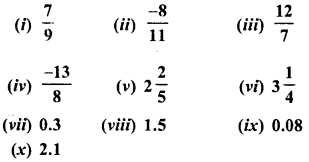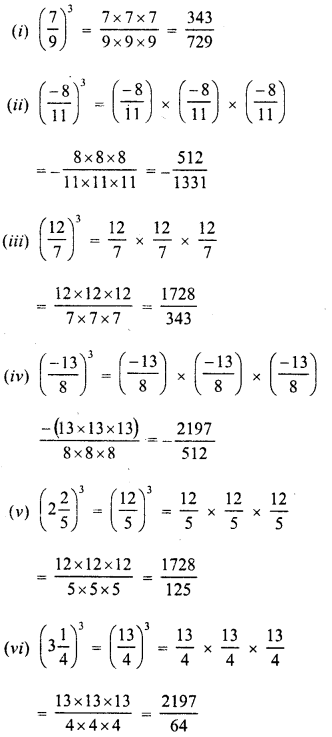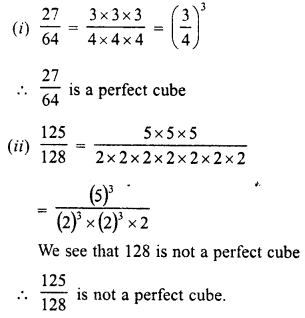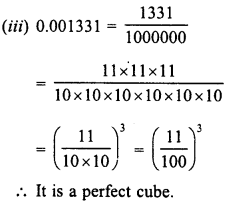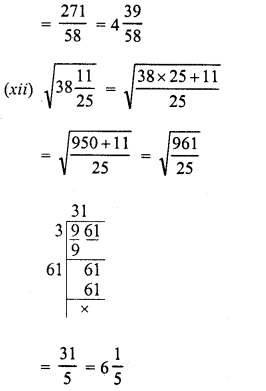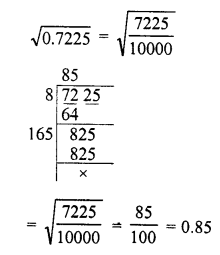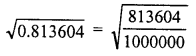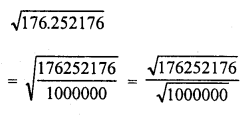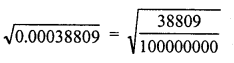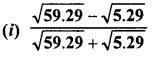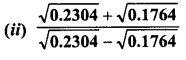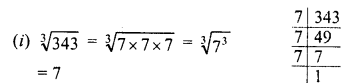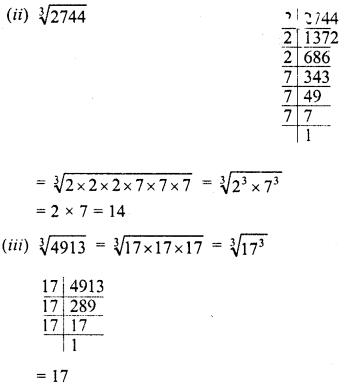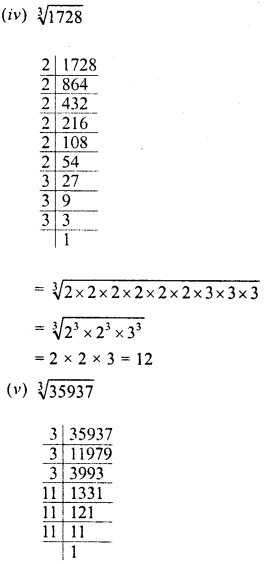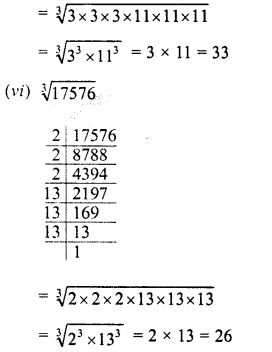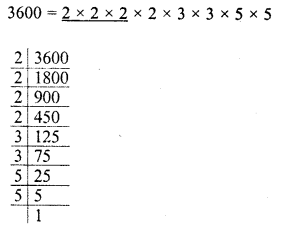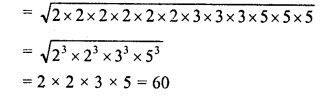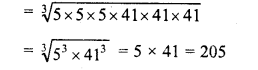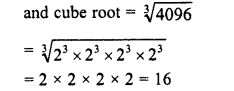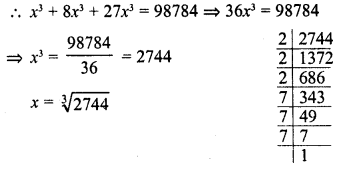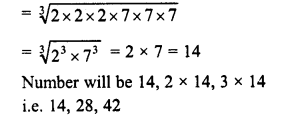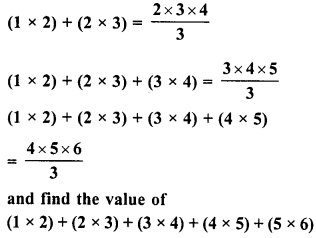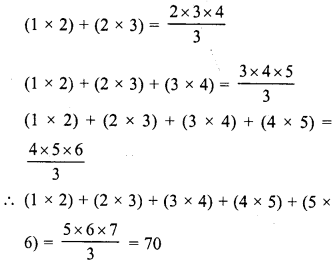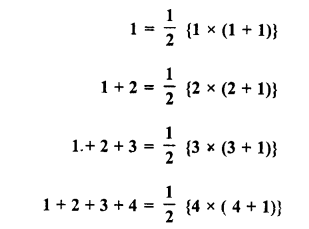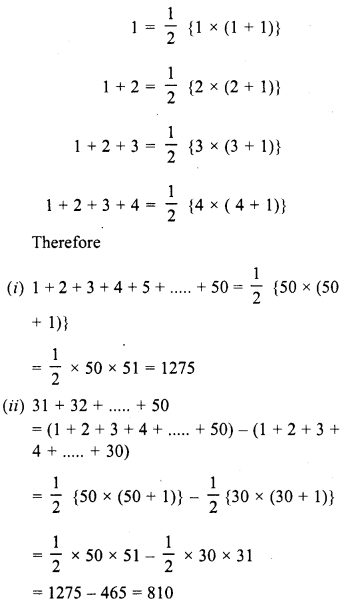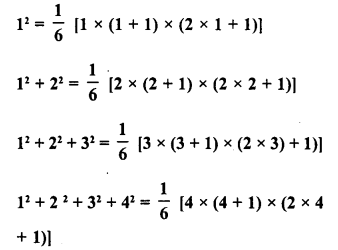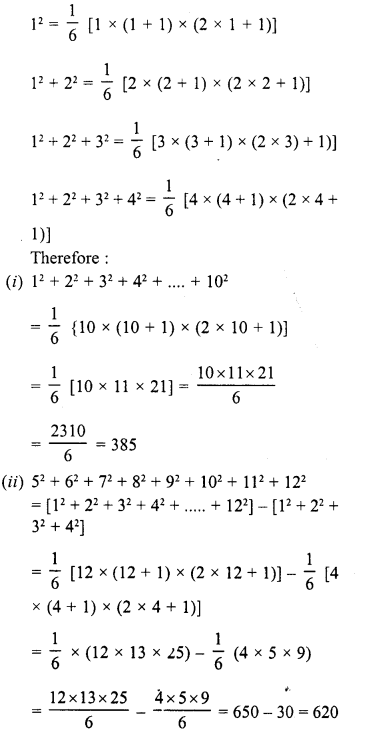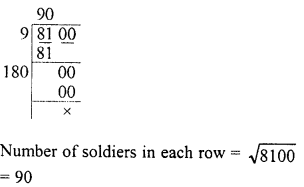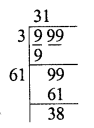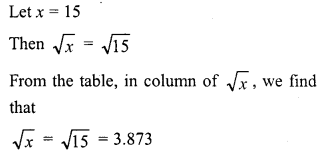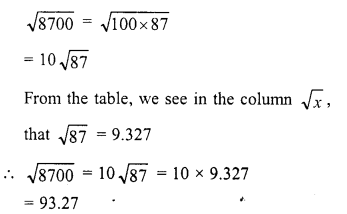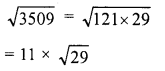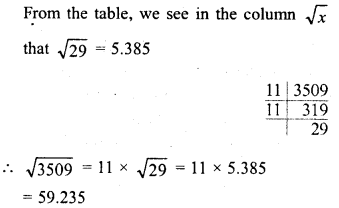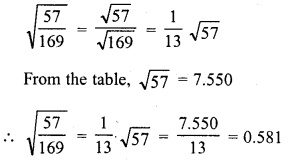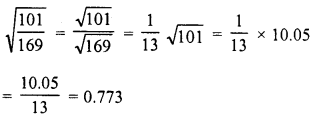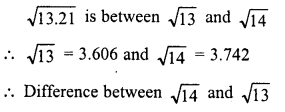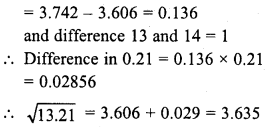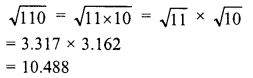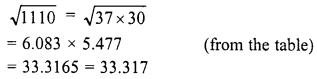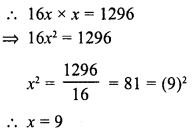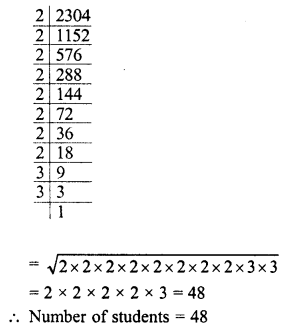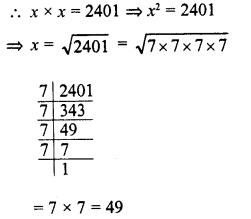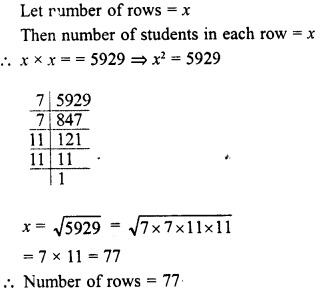RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.4
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5

Question 1.
Find the cubes of the following numbers:
(i) 7
(ii) 12
(iii) 16
(iv) 21
(v) 40
(vi) 55
(vii) 100
(viii) 302
(ix) 301
Solution:
(i) (7)³ = 7 x 7 x 7 = 343
(ii) (12)³ = 12 x-12 x 12 = 1728
(iii) (16)³ = 16 x 16 x 16 = 4096
(iv) (21)³ = 21 x 21 x 21 = 441 x 21 =9261
(v) (40)³ = 40 x 40 x 40 = 64000
(vi) (55)³ = 55 x 55 x 55 = 3025 x 55 = 166375
(vii) (100)³ = 100 x 100 x 100 =1000000
(viii)(302)³ = 302 x 302 x 302 = 91204 x 302 = 27543608
(ix) (301)³ = 301 x 301 x 301 = 90601 x 301 =27270901

Question 2.
Write the cubes of all natural numbers between 1 and 10 and verify the following statements :
(i) Cubes of all odd natural numbers are odd.
(ii) Cubes of all even natural numbers are even.
Solution:
Cubes of first 10 natural numbers :
(1)³ = 1 x 1 x 1 = 1
(2)³ = 2 x 2 x 2 = 8
(3)³ = 3 x 3 x 3 = 27
(4)³= 4 x 4 x 4 = 64
(5)³ = 5 x 5 x 5 = 125
(6)³ = 6 x 6 x 6 = 216
(7)³ = 7 x 7 x 7 = 343
(8)³ = 8 x 8 x 8 = 512
(9)³ = 9 x 9 x 9= 729
(10)³ = 10 x 10 x 10= 1000
We see that the cubes of odd numbers is also odd and cubes of even numbers is also even.

Question 3.
Observe the following pattern :

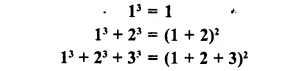
Write the next three rows and calculate the value of 1³ + 2³ + 3³ +…. + 9³ + 10³ by the above pattern.
Solution:
We see the pattern

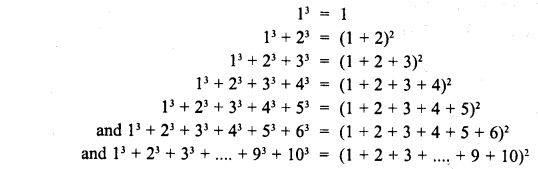
Question 4.
Write the cubes of 5 natural numbers which are multiples of 3 and verify the followings :
The cube of a natural number which is a multiple of 3 is a multiple of 27′
Solution:
5 natural numbers which are multiples of 3
3,6,9,12,15.
(3)³ = 3 x 3 x 3 = 27
Which is multiple of 27
(6)³ = 6 x 6 x 6 = 216 ÷ 27 = 8
Which is multiple of 27
(9)³ = 9 x 9 x 9 = 729 + 27 = 27
Which is multiple of 27
(12)³= 12 x 12 x 12 = 1728 ÷ 27 = 64
Which is multiple of 27
(15)³ = 15 x 15 x 15 = 3375 ÷ 27 = 125
Which is multiple of 27
Hence, cube of multiple of 3 is a multiple of 27

Question 5.
Write the cubes of 5 natural numbers which are of the form 3n+ 1 (e.g.,4, 7, 10, …………) and verify the following :
‘The cube of a natural number of the form 3n + 1 is a natural number of the same form i.e. when divided by 3 it leaves the remainder 1’.
Solution:
3n + 1
Let n = 1, 2, 3, 4, 5, then
If n = 1, then 3n +1= 3 x 1+1= 3+1= 4
If n = 2, then 3n +1=3 x 2+1=6+1=7
If n = 3, then 3n + 1= 3 x 3 + 1= 9 + 1 = 10
If n = 4, then 3n + 1= 3 x 4+1 = 12 + 1= 13
If n = 5, then 3n +1=3 x 5 + 1 = 15 +1 = 16
Now
(4)³ = 4 x 4 x 4 = 64
Which is \(\frac {64 }{ 3 }\)=21, Remainder = 1
(7)³ = 7 x 7 x 7 = 343
Which is \(\frac {343 }{ 3 }\) =114, Remainder = 1
(10)³ = 10 x 10 x 10 = 1000 ÷ 3 = 333, Remainder = 1
(13)³ = 13 x 13 x 13 = 2197 ÷ 3 = 732, Remainder = 1
(16)³ = 16 x 16 x 16 = 4096 ÷ 3 = 1365, Remainder = 1
Hence cube of natural number of the form, 3n + 1, is a natural of the form 3n + 1

Question 6.
Write the cubes of 5 natural numbers of the form 3n + 2 (i.e. 5, 8, 11,……… ) and verify the following :
‘The cube of a natural number of the form 3n + 2 is a natural number of the same form i.e. when it is dividend by 3 the remainder is 2’.
Solution:
Natural numbers of the form 3n + 2, when n
is a natural number i.e. 1, 2, 3, 4, 5,………….
If n = 1, then 3n + 2 = 3 x 1+2 = 3+ 2 = 5
If n = 2, then 3n + 2 = 3 x 2 + 2 = 6 + 2 = 8
If n = 3, then 3n + 2 = 3 x 3 + 2 = 9 + 2 = 11
If n = 4, then 3n + 2 = 3 x 4 + 2 = 12 + 2 = 14
and if n = 5, then 3n + 2 = 3 x 5 + 2 = 15 + 2= 17
Now (5)³ = 5 x 5 x 5 = 125
125 + 3 = 41, Remainder = 2
(8)² = 8 x 8 x 8 = 512 512 -s- 3 = 170, Remainder = 2
(11)³ = 11 x 11 x 11 = 1331
1331 + 3 = 443, Remainder = 2
(14)³ = 14 x 14 x 14 = 2744
2744 + 3 = 914, Remainder = 2
(17)³ = 17 x 17 x 17 = 4913
4913 = 3 = 1637, Remainder = 2
We see the cube of the natural number of the
form 3n + 2 is also a natural number of the
form 3n + 2.

Question 7.
Write the cubes of 5 natural numbers of which are multiples of 7 and verify the following :
‘The cube of a multiple of 7 is a multiple of 7^3′.
Solution:
5 natural numbers which are multiple of 7,are 7, 14, 21, 28, 35
(7)³ = (7)³ which is multiple of 7³
(14)³ = (2 x 7)3 = 2³ x 7³, which is multiple of 7³
(21)³ = (3 x 7)3 = 33 x 7³_, which is multiple of 7³
(28)³ = (4 x 7)³ = 4³ x 7³, which is multiple of 7³ (35)³ = (5 x 7)³ = 5³ x 73 which is multiple of 7³
Hence proved.

Question 8.
Which of the following are perfect cubes?
(i) 64
(ii) 216
(iii) 243
(iv) 1000
(v) 1728
(vi) 3087
(vii) 4608
(viii) 106480
(ix) 166375
(x) 456533
Solution:
(i) 64 = 2 x 2 x 2 x 2 x 2 x 2

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 64 is a perfect cube
(ii) 216 = 2 x 2 x 2 x 3 x 3 x 3

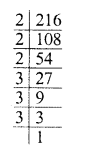
Grouping the factors in triplets of equal factors, we see that no factor is left
216 is a perfect cube.
(iii) 243 = 3 x 3 x 3 x 3 x 3

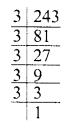
Grouping the factors in triplets, we see that two factors 3 x 3 are left
∴ 243 is not a perfect cube.
(iv) 1000 = 2 x 2 x 2 x 5 x 5 x 5

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 1000 is a perfect cube.
(v) 1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors in triplets of the equal factors, we see that no factor is left
∴ 1728 is a perfect cube,
(vi) 3087 = 3 x 3 x 7 x 7 x 7

Grouping the factors in triplets of the equal factors, we see that two factor 3×3 are left
∴ 3087 is not a perfect cube.
(vii) 4608 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3

Grouping the factors in triplets of equal factors, we see that two factors 3, 3 are left
∴ 4609 is not a perfect cube.
(viii) 106480 = 2 x 2 x 2 x 2 x 5 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, we see that factors 2, 5 are left
∴ 106480 is not a perfect cube.
(ix) 166375 = 5 x 5 x 5 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 166375 is a perfect cube.
(x) 456533 = 7 x 7 x 7 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, we see that no factor is left
∴ 456533 is a perfect cube.

Question 9.
Which of the following are cubes of even natural numbers ?
216, 512, 729,1000, 3375, 13824
Solution:
We know that the cube of an even natural number is also an even natural number
∴ 216, 512, 1000, 13824 are even natural numbers.
∴ These can be the cubes of even natural number.

Question 10.
Which of the following are cubes of odd natural numbers ?
125, 343, 1728, 4096, 32768, 6859
Solution:
We know that the cube of an odd natural number is also an odd natural number,
∴ 125, 343, 6859 are the odd natural numbers
∴ These can be the cubes of odd natural numbers.

Question 11.
What is the smallest number by which the following numbers must be multiplied, so that the products are perfect cubes ?
(i) 675
(ii) 1323
(iii) 2560
(iv) 7803
(v) 107311
(vi) 35721
Solution:
(i) 675 = 3 x 3 x 3 x 5 X 5

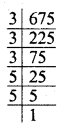
Grouping the factors in triplet of equal factors, 5 x 5 are left without triplet
So, by multiplying by 5, the triplet will be completed.
∴ Least number to be multiplied = 5
(ii) 1323 = 3 x 3 x 3 x 7 x 7

Grouping the factors in triplet of equal factors. We find that 7 x 7 has been left
So, multiplying by 7, we get a triplet
∴ The least number to be multiplied = 7
(iii) 2560 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 5

Grouping the factors in triplet of equal factors, 5 is left.
∴ To complete a triplet 5 x 5 is to multiplied
∴ Least number to be multiplied = 5 x 5 = 25
(iv) 7803 = 3 x 3 x 3 x 17 x 17

Grouping the factors in triplet of equal factors, we find the 17 x 17 are left
So, to complete the triplet, we have to multiply by 17
∴ Least number to be multiplied = 17
(v) 107811 = 3 x 3 x 3 x 3 x 11 x 11 x 11

Grouping the factors in triplet of equal factors, factor 3 is left
So, to complete the triplet 3 x 3 is to be multiplied
∴ Least number to be multiplied = 3 x 3 = 9
(vi) 35721 = 3 x 3 x 3 x 3 x 3 x 3 x 7 x 7

Grouping the factors in triplet of equal factors, we find that 7 x 7 is left
So, in order to complete the triplets, we have to multiplied by 7
∴ Least number to be multiplied = 7

Question 12.
By which smallest number must the following numbers be divided so that the quotient is a perfect cube ?
(i) 675
(ii) 8640
(iii) 1600
(iv) 8788
(v) 7803
(vi) 107811
(vii) 35721
(viii) 243000
Solution:
(i) 675 = 3 x 3 x 3 x 5 x 5

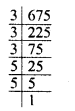
Grouping the factors in triplet of equal factors, 5 x 5 is left
5 x 5 is to be divided so that the quotient will be a perfect cube.
∴ The least number to be divided = 5 x 5 = 25
(ii) 8640 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors in triplets of equal factors, 5 is left
∴ In order to get a perfect cube, 5 is to divided
∴ Least number to be divided = 5
(iii) 1600 = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5

Grouping the factors in triplets of equal factors, we find that 5 x 5 is left
∴ In order to get a perfect cube 5 x 5 = 25 is to be divided.
∴ Least number to be divide = 25
(iv) 8788 = 2 x 2 x 13 x 13 x 13

Grouping the factors in triplets of equal factors, we find that 2 x 2 has been left
∴ In order to get a perfect cube, 2 x 2 is to be divided
∴ Least number to be divided = 4
(v) 7803 = 3 x 3 x 3 x 17 x 17

Grouping the factors in triplets of equal factors, we see that 17 x 17 has been left.
So, in order to get a perfect cube, 17 x 17 is be divided
∴ Least number to be divided = 17 x 17 = 289
(vi) 107811 = 3 x 3 x 3 x 3 x 11 x 11 x 11

Grouping the factors in triplets of equal factors, 3 is left
∴ In order to get a perfect cube, 3 is to be divided
∴ Least number to be divided = 3
(vii) 35721 = 3 x 3 x 3 x 3 x 3 x 3 x 7 x 7

Grouping the factors in triplets of equal factors, we see that 7 x 7 is left
So, in order to get a perfect cube, 7 x 7 = 49 is to be divided
∴ Least number to be divided = 49
(viii) 243000 = 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 5 x 5 x 5

Grouping the factors in triplets of equal factors, 3 x 3 is left
∴ By dividing 3 x 3, we get a perfect cube
∴ Least number to be divided = 3 x 3=9

Question 13.
Prove that if a number is trebled then its cube is 27 times the cube of the given number.
Solution:
Let x be the number, then trebled number of x = 3x
Cubing, we get:
(3x)³ = (3)³ x³ = 27x³
27x³ is 27 times the cube of x i.e., of x³

Question 14.
What happenes to the cube of a number if the number is multiplied by
(i) 3 ?
(ii) 4 ?
(iii) 5 ?
Solution:
number (x)³ = x³
(i) If x is multiplied by 3, then the cube of
∴ (3x)³ = (3)³ x x³ = 27x³
∴ The cube of the resulting number is 27 times of cube of the given number
(ii) If x is multiplied by 4, then the cube of
(4x)³ = (4)³ x x³ = 64x³
∴ The cube of the resulting number is 64 times of the cube of the given number
(ii) If x is multiplied by 5, then the cube of
(5x)³ = (5)³ x x³ = 125x³
∴ The cube of the resulting number is 125 times of the cube of the given number

Question 15.
Find the volume of a cube, one face of which has an area of 64 m².
Solution:
Area of one face of a cube = 64 m²
∴ Side (edge) of cube = √64
= √64 = 8 m
∴ Volume of the cube = (side)³ = (8 m)³ = 512 m³

Question 16.
Find the volume of a cube whose surface area is 384 m².
Solution:
Surface area of a cube = 384 m² Let side = a
Then 6a² = 384 ⇒ a² = \(\frac {384 }{ 6 }\)= 64 = (8)²
∴ a = 8 m
Now volume = a³ = (8)³ m³ = 512 m³

Question 17.
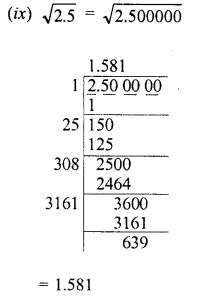
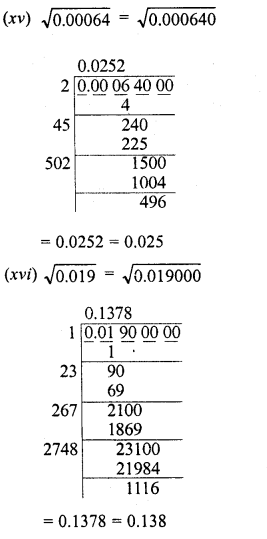
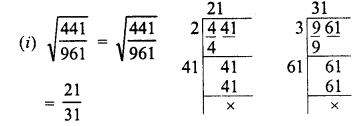
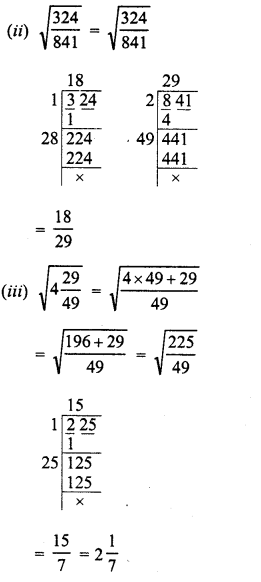
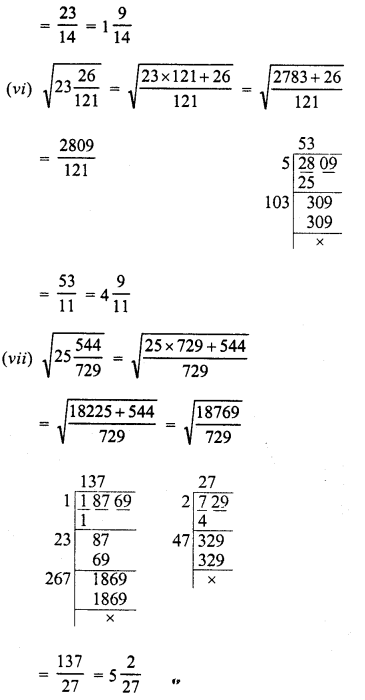
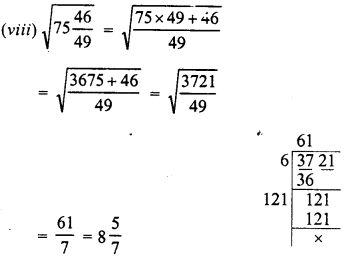
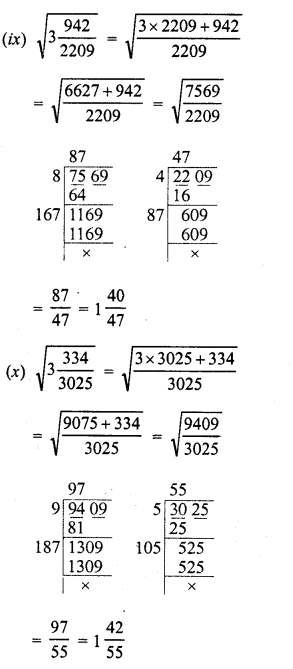
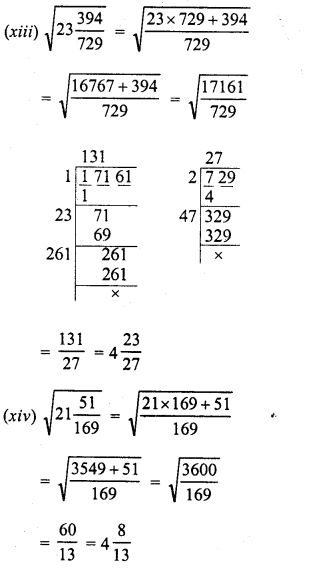
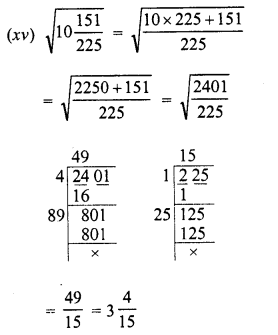
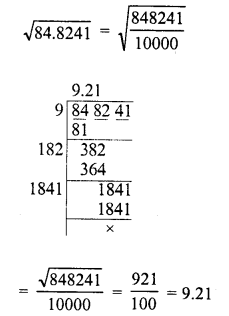
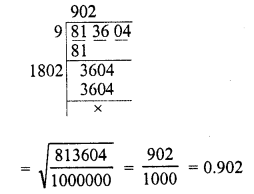
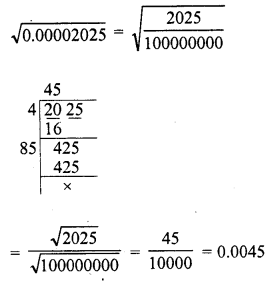
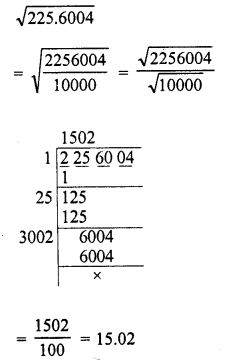
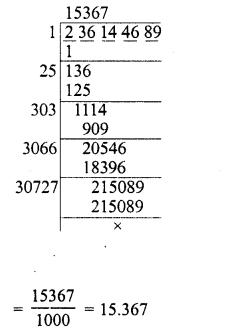
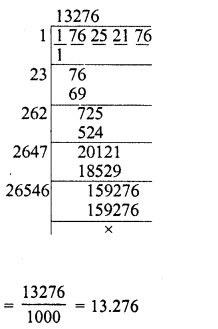
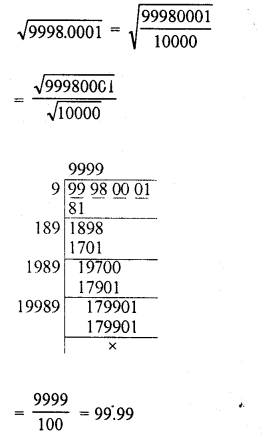
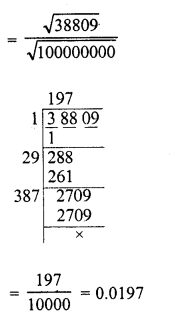
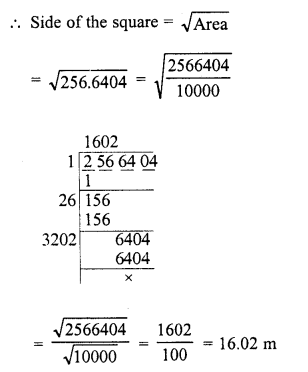
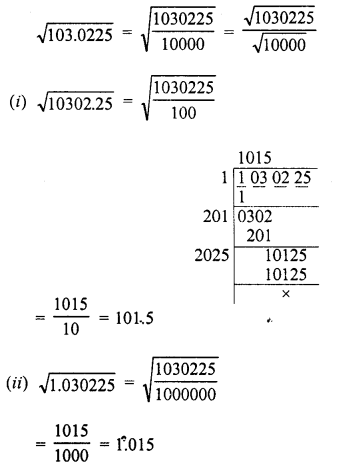
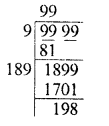
Evaluate the following :

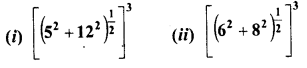
Solution:

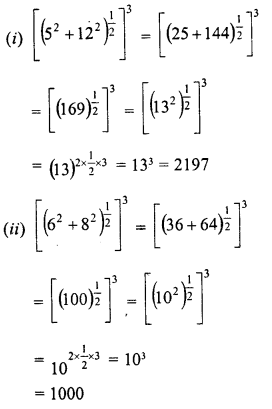
Question 18.
Write the units digit of the cube of each of the following numbers :
31,109,388,833,4276,5922,77774,44447, 125125125.
Solution:
We know that if unit digit of a number n is
= 1, then units digit of its cube = 1
= 2, then units digit of its cube = 8
= 3, then units digit of its cube = 7
= 4, then units digit of its cube = 4
= 5, then units digit of its cube = 5
= 6, then units digit of its cube = 6
= 7, then the units digit of its cube = 3
= 8, then units digit of its cube = 2
= 9, then units digit of its cube = 9
= 0, then units digit of its cube = 0
Now units digit of the cube of 31 = 1
Units digit of the cube of 109 = 9
Units digits of the cube of 388 = 2
Units digits of the cube of 833 = 7
Units digits of the cube of 4276 = 6
Units digit of the cube of 5922 = 8
Units digit of the cube of 77774 = 4
Units digit of tl. cube of 44447 = 3
Units digit of the cube of 125125125 = 5

Question 19.
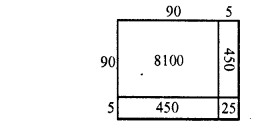
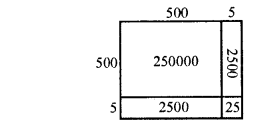
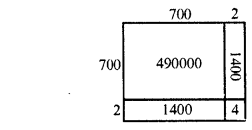
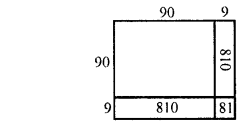
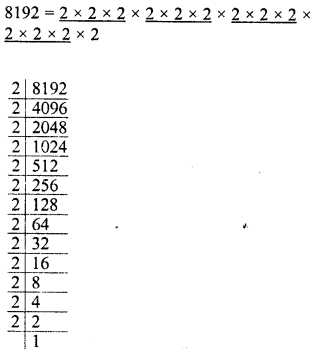
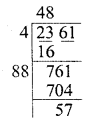
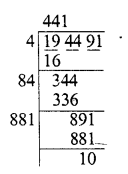
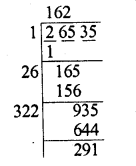
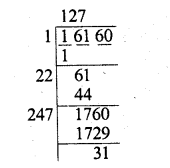
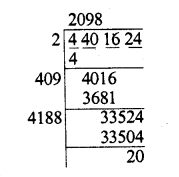
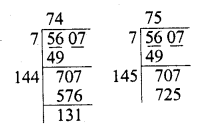
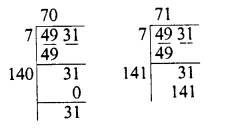
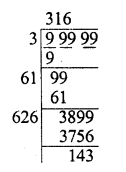
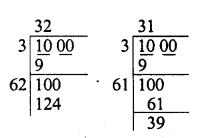
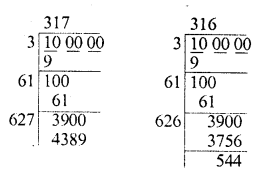
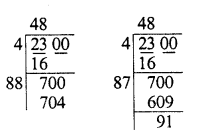
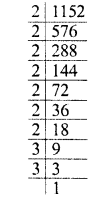
Find the cubes of the following numbers by column method :
(i) 35
(ii) 56
(iii) 72
Solution:

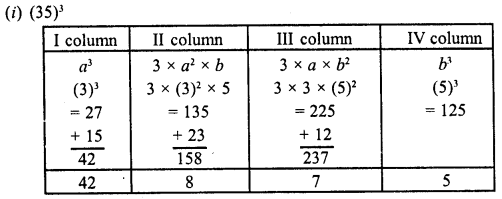
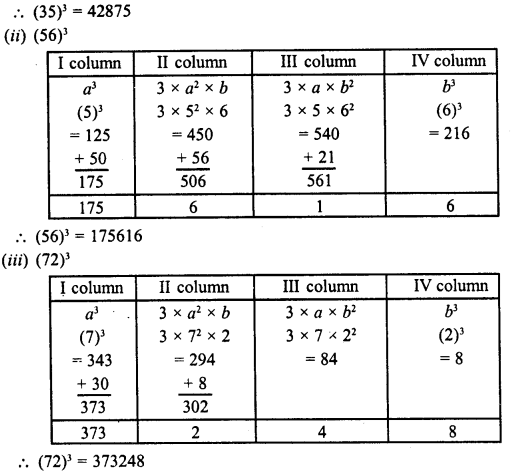
Question 20.
Which of the following numbers are not perfect cubes ?
(i) 64
(ii) 216
(iii) 243
(iv) 1728
Solution:
(i) 64 = 2 x 2 x 2 X 2 x 2 x 2

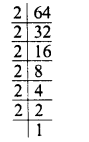
Grouping the factors in triplets, of equal factors, we see that no factor is left
∴ 64 is a perfect cube.
(ii) 216 = 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors in triplets, of equal factors, we see that no factor is left
∴ 216 is a perfect cube.
(iii) 243 = 3 x 3 x 3 x 3 x 3

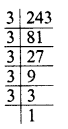
Grouping the factors in triplets, of equal factors, we see that 3 x 3 are left
∴ 243 is not a perfect cube.
(iv) 1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

Grouping the factors m triplets, of equal factors, we see that no factor is left.
∴ 1728 is a perfect cube.

Question 21.
For each of the non-perfect cubes, in Q. 20, find the smallest number by which it must be
(a) multiplied so that the product is a perfect cube.
(b) divided so that the quotient is a perfect cube.
Solution:
In qustion 20, 243 is not a perfect cube and 243 = 3 x 3 x 3 x 3 x 3
Grouping the factors in triplets, of equal factors, we see that 3 x 3 is left.
(a) In order to make it a perfect cube, 3 is to be multiplied which makes a triplet.
(b) In order to make it a perfect cube, 3 x 3 or 9 is to be divided.

Question 22.
By taking three different values of n verify the truth of the following statements :
(i) If n is even, then n³ is also even.
(ii) If n is odd, then n³ is also odd.
(iii) If n leaves remainder 1 when divided by 3, then it3 also leaves 1 as remainder when divided by 3.
(iv) If a natural number n is of the form 3p + 2 then n³ also a number of the same type.
Solution:
(i) n is even number.
Let n = 2, 4, 6 then
(a) n³ = (2)³ = 2 x 2 x 2 = 8, which is an even number.
(b) (n)³= (4)³ = 4 x 4 x 4 = 64, which is an even number.
(c) (n)³ = (6)³ = 6 x 6 x 6 = 216, which is an even number.

(ii) n is odd number.
Letx = 3, 5, 7
(a) (n)³ = (3)³ = 3 x 3 x 3 = 27, which is an odd number.
(b) (n)³ = (5)³ = 5 x 5 x 5 = 125, which is an odd number.
(c) (n)³ = (7)³ = 7 x 7 x 7 = 343, which is an odd number.

(iii) If n leaves remainder 1 when divided by 3, then n³ is also leaves 1 as remainder,
Let n = 4, 7, 10 If n = 4,
then «³ = (4)³ = 4 x 4 x 4 = 64
= 64 + 3 = 21, remainder = 1
If n = 7, then
n³ = (7)³ = 7 x 7 x 7 = 343
343 + 3 = 114, remainder = 1
If n – 10, then
(n)³ = (10)³ = 10 x 10 x 10 = 1000
1000 + 3 = 333, remainder = 1

(iv) If the natural number is of the form 3p + 2, then n³ is also of the same type
Let p =’1, 2, 3, then
(a) If p = 1, then
n = 3p + 2 = 3 x 1+2=3+2=5
∴ n³ = (5)³ = 5 x 5 x 5 = 125
125 = 3 x 41 + 2 = 3p +2

(b) If p = 2, then
n = 3p + 2 = 3 x 2 + 2 = 6 + 2 = 8
∴ n³ = (8)³ = 8 x 8 x 8 = 512
∴ 512 = 3 x 170 + 2 = 3p + 2

(c) If p = 3, then
n = 3p + 2 = 3 x 3 + 2 = 9 + 2 = 11
∴ n³ = (11)³ = 11 x 11 x 11 = 1331
and 1331 =3 x 443 + 2 = 3p + 2
Hence proved.

Question 23.
Write true (T) or false (F) for the following statements :
(i) 0 392 is a perfect cube.
(ii) 8640 is not a perfect cube.
(iii) No cube can end with exactly two zeros.
(iv) There is no perfect cube which ends in 4.
(v) For an integer a, a³ is always greater than a² > b²
(vi) If a and b are integers such that a² > b² , then a³ > b³.
(x) If a² ends in an even number of zeros, then a ends in an odd number of zeros.
Solution:

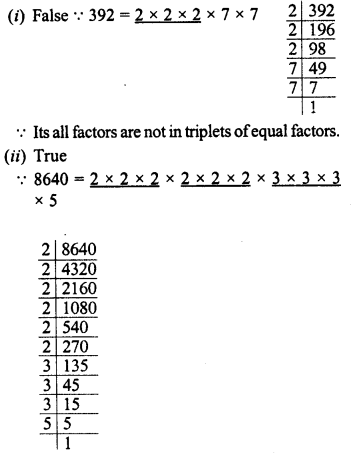
∵ 5 is left.
(iii)True : A number ending three zeros can be a perfect cube.
(iv) False : v (4)³ = 4 x 4 x 4 = 64, which ends with 4.
(v) False : If n is a proper fraction, it is not possible.
(vi) False : It is not true if a and b are proper fraction.
(vii) True.
(viii) False : as a² ends in 9, then a³ does not necessarily ends in 7. It ends in 3 also.
(ix) False : it is not necessarily that a³ ends in 25 it can end also in 75.
(x) False : If a² ends with even zeros, then a³ will ends with odd zeros but of multiple of 3.

 

Hope given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
Find the square root of each of the following correct to three places of decimal :
(i) 5
(ii) 7
(iii) 17
(iv) 20
(v) 66
(vi) 427
(vii) 1.7
(vii’) 23.1
(ix) 2.5
(x) 237.615
(xi) 15.3215
(xii) 0.9
(xiii) 0.1
(xiv) 0.016
(xv) 0.00064
(xvi) 0.019
(xvii) \(\frac {7 }{ 8 }\)
(xviii) \(\frac {5 }{ 12 }\)
(xix) 2 \(\frac {1 }{ 2 }\)
(xx) 287 \(\frac {8 }{ 8 }\)
Solution:

Question 2.
Find the square root of 12.0068 correct to four decimal places.
Solution:

Question 3.
Find the square root of 11 correct to five decimal places.
Solution:

Question 4.
Given that √2, = 1-414, √3 = 1.732, √5 = 2.236 and √7 = 2.646. Evaluate each of the following :

Solution:

Question 5.
Given that √2 = 1-414, √3 = 1-732, √5= 2.236 and √7= 2.646, find the square roots of the following :

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.4
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5

Question 1.
Find the cubes of:
(i) -11
(ii) -12
(iii) – 21
Solution:
(i) (-11)³=(-11)³=(11 x 11 x 11) =-1331
(ii) (-12)³=(-12)³=(12 x 12 x 12) =  -1728
(iii) (-21)³=(-21)³=(21 x 21 x 21) = -9261

Question 2.
Which of the following numbers are cubes of negative integers.
(i) -64
(ii) -1056
(iii) -2197
(iv) -2744
(v)  -42875
Solution:


∴ All factors of 64 can be grouped in triplets of the equal factors completely.
∴ -64 is a perfect cube of negative integer.

All the factors of 1056 can be grouped in triplets of equal factors grouped completely
∴ 1058 is not a perfect cube of negative integer.

All the factors of -2197 can be grouped in triplets of equal factors completely
∴ 2197 is a perfect cube of negative integer,

All the factors of -2744 can be grouped in triplets of equal factors completely
∴ 2744 is a perfect cube of negative integer

All the factors of -42875 can be grouped in triplets of equal factors completely
∴ 42875 is a perfect cube of negative integer.

Question 3.
Show that the following integers are cubes of negative integers. Also, find the integer whose cube is the given integer :
(i) -5832 (ii) -2744000
Solution:


Grouping the factors in triplets of equal factors, we see that no factor is left
∴ -5832 is a perfect cube
Now taking one factor from each triplet we find that
-5832 is a cube of – (2 x 3 x 3) = -18
∴ Cube root of-5832 = -18

Grouping the factors in tuplets of equal factors, we see that no factor is left. Therefore it is a perfect cube.
Now taking one factor from each triplet, we find that.
-2744000 is a cube of – (2 x 2 x 5 x 7) ie. -140
∴ Cube root of -2744000 = -140

Question 4.
Find the cube of :

Solution:

Question 5.
Which of the following numbers are cubes of rational numbers :

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
Find the square root of:


Solution:

Question 2.
Find the value of :

Solution:

Question 3.
The area of a square field is 80 \(\frac {244 }{ 729 }\) square metres. Find the length of each side of the field.
Solution:

Question 4.
The area of a square field is 30 \(\frac {1 }{ 4}\) m². Calculate the length of the side of the squre.
Solution:

Question 5.
Find the length of a side of a square playground whose area is equal to the area of a rectangular field of dimensions 72 m and 338 m.
Solution:
Length of rectangular field (l) = 338 m
and breadth (b) = 72 m
∴ Area = 1 x 6= 338 x 72 m²
∴ Area of square = 338 x 72 m² = 24336 m²
and length of the side of the square

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
Find the squares of the following numbers using column method. Verify the result by finding the square using the usual multiplication :
(i) 25
(ii) 37
(iii) 54
(iv) 71
(v) 96
Solution:
(i) (25)²

Question 2.
Find the squares of the following numbers using diagonal method :
(i) 98
(ii) 273
(iii) 348
(iv) 295
(v) 171
Solution:

Question 3.
Find the squares of the following numbers :
(i) 127
(ii) 503
(iii) 451
(iv) 862
(v) 265
Solution:
(i) (127)² = (120 + 7)²
{(a + b)² = a² + lab + b²}
= (120)² + 2 x 120 x 7 + (7)²
= 14400+ 1680 + 49 = 16129

(ii) (503)² = (500 + 3)²
{(a + b)² = a² + lab + b¹}
= (500)² + 2 x 500 x 3 + (3)²
= 250000 + 3000 + 9 = 353009

(iii) (451)² = (400 + 51)²
{(a + b)² = a² + lab + b²}
= (400)² + 2 x 400 x 51 + (5l)²
= 160000 + 40800 + 2601 = 203401

(iv) (451)² = (800 + 62)²
{(a + b)² = a² + lab + b²}
= (800)² + 2 x 800 x 62 + (62)²
= 640000 + 99200 + 3844 = 743044

(v) (265)²
{(a + b)² = a² + 2ab + b²}
(200 + 65)² = (200)² + 2 x 200 x 65 + (65)²
= 40000 + 26000 + 4225 = 70225

Question 4.
Find the squares of the following numbers
(i) 425
(ii) 575
(iii) 405
(iv) 205
(v) 95
(vi) 745
(vii) 512
(viii) 995
Solution:
(i) (425)²
Here n = 42
∴ n (n + 1) = 42 (42 + 1) = 42 x 43 = 1806
∴ (425)² = 180625

(ii) (575)²
Here n = 57
∴ n (n + 1) = 57 (57 + 1) = 57 x 58 = 3306
∴ (575)² = 330625

(iii) (405)²
Here n = 40
∴ n (n + 1) = 40 (40 + 1) -40 x 41 = 1640
∴ (405)² = 164025

(iv) (205)²
Here n = 20
∴ n (n + 1) = 20 (20 + 1) = 20 x 21 = 420
∴ (205)² = 42025

(v) (95)²
Here n = 9
∴ n (n + 1) = 9 (9 + 1) = 9 x 10 = 90
∴ (95)² = 9025

(vi) (745)²
Here n = 74
∴ n (n + 1) = 74 (74 + 1) = 74 x 75 = 5550
∴ (745)² = 555025

(vii) (512)²
Here a = 1, b = 2
∴ (5ab)² = (250 + ab) x 1000 + (ab)²
∴ (512)² = (250 + 12) x 1000 + (12)²
= 262 x 1000 + 144
= 262000 + 144 = 262144

(viii) (995)²
Here n = 99
∴ n (n + 1) = 99 (99 + 1) = 99 x 100 = 9900
∴ (995)² = 990025

Question 5.
Find the squares of the following numbers using the identity (a + b)1 = a2 + lab + b1
(i) 405
(ii) 510
(iii) 1001
(iv) 209
(v) 605
Solution:
a + b)² = a² + lab + b²

(i) (405)² = (400 + 5)²
= (400)² + 2 x 400 x 5 + (5)²
= 160000 + 4000 + 25 = 164025

(ii) (510)² = (500 + 10)²
= (500)² + 2 x 500 x 10 x (10)²
= 250000 + 10000 + 100
= 260100

(iii) (1001)² = (1000+1)²
= (1000)² + 2 X 1000 x 1 + (1)
= 1000000 + 2000 + 1
=1002001

(iv) (209)² = (200 + 9)²
= (200)² + 2 x 200 x 9 x (9)²
= 40000 + 3600 +81
= 43681

(v) (605)² = (600 + 5)²
= (600)² + 2 x 600 x 5 +(5)²
= 360000 + 6000       25
=366025

Question 6.
Find the squares of the following numbers using the identity (a – b)² = a² – 2ab + b² :
(i) 395
(ii) 995
(iii) 495
(iv) 498
(v) 99
(vi) 999
(vii) 599
Solution:
a – b)² = a² – lab + b²

(i) (395)² = (400 – 5)²
= (400)² – 2 x 400 x 5 + (5)²
= 160000-4000 + 25
= 160025-4000
= 156025

(ii) (995)² = (1000 – 5)²
= (1000)² – 2 x 1000 x 5 + (5)²
= 1000000- 10000 + 25
= 1000025- 10000
= 990025

(iii) (495)² = (500 – 5)²
= (500)² – 2 x 500 x 5 + (5)²
= 250000 – 5000 + 25
= 250025 – 5000
= 245025

(iv) (498)² = (500 – 2)²
= (500)² – 2 x 500 x 2 + (2)²
= 250000 – 2000 + 4
= 250004 – 2000
= 248004

(v) (99)² = (100 – l)²
= (100)² – 2 x 100 x 1 + (1)²
= 10000 – 200 + 1
= 10001 – 200
= 9801

(vi) (999)² = (1000- l)²
= (1000)² – 2 x 1000 x 1+ (1)2
= 1000000-2000+1
= 10000001-2000=998001

(vii) (599)² = (600 – 1)²
= (600)² -2 x 600 X 1+ (1)2
= 360000 -1200+1
= 360001 – 1200 = 358801

Question 7.
Find the squares of the following numbers by visual method :
(i) 52
(ii) 95
(iii) 505
(iv) 702
(v) 99
Solution:
(a + b)² = a² – ab + ab + b²
(i) (52)² = (50 + 2)²
= 2500 + 100 + 100 + 4
= 2704

(ii) (95)² = (90 + 5)²
= 8100 + 450 + 450 + 25
= 9025

(iii) (505)² = (500 + 5)²
= 250000 + 2500 + 2500 + 25
= 255025

(iv) (702)² = (700 + 2)²
= 490000 + 1400+ 1400 + 4
= 492804

(v) (99)² = (90 + 9)²
= 8100 + 810 + 810 + 81
= 9801

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Find the square root of the following numbers in decimal form :

Question 1.
84.8241
Solution:

Question 2.
0.7225
Solution:

Question 3.
0.813604
Solution:

Question 4.
0.00002025
Solution:

Question 5.
150.0625
Solution:

Question 6.
225.6004
Solution:

Question 7.
3600.720036
Solution:

Question 8.
236.144689
Solution:

Question 9.
0.00059049
Solution:

Question 10.
176.252176
Solution:

Question 11.
9998.0001
Solution:

Question 12.
0.00038809
Solution:

Question 13.
What is that fraction which when multiplied by itself gives 227.798649 ?
Solution:

Question 14.
square playground is 256.6404 square metres. Find the length of one side of the playground.
Solution:
Area of square playground = 256.6404 sq. m

Question 15.
What is the fraction which when multiplied by itself gives 0.00053361 ?
Solution:

Question 16.
Simplify :


Solution:

Question 17.
Evaluate \(\sqrt { 50625 }\) and hence find the value of \(\sqrt { 506.25 } +\sqrt { 5.0625 } \).
Solution:

Question 18.
Find the value of \(\sqrt { 103.0225 }\) and hence And the value of

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.4
• RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5

Question 1.
Find the cube roots of the following numbers by successive subtraction of numbers : 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397,
(i) 64
(ii) 512
(iii) 1728
Solution:
(i) 64
64 – 1 = 63
63 – 7 = 56
56 – 19 = 37
37 – 37 = 0
∴ 64 = (4)³
∴ Cube root of 64 = 4

(ii) 512
512 -1 =511
511- 7 = 504
504 – 19 = 485
485 – 37 = 448
448 – 61 = 387
387 – 91 =296
296 – 127 = 169
169 – 169 = 0
∴ 512 = (8)³
∴ Cube root of 512 = 8

(iii) 1728
1728 – 1= 1727
1727 -7 = 1720
1720 -19 = 1701
1701 -37= 1664
1664 – 61 = 1603
1603 – 91 = 1512
1512 -127= 1385 .
1385 – 169= 1216
1216 – 217 = 999
999 – 271 =728
728 – 331 = 397
397 – 397=0
∴ 1728 = (12)³
∴ Cube root of 1728 = 1²

Question 2.
Using the method of successive subtraction, examine whether or not the following numbers are perfect cubes :
(i) 130
(ii) 345
(iii) 792
(iv) 1331
Solution:
(i) 130
130 – 1 = 129
129 -7 = 122
122 -19 = 103
103 -37 = 66
66 – 61 = 5
We see that 5 is left
∴ 130 is not a perfect cube.

(ii) 345
345 – 1 = 344
344 – 7 = 337
337 – 19 = 318
318 – 37 = 281
81 – 61 =220
220 – 91 = 129
129 – 127 = 2
We see that 2 is left
∴ 345 is not a perfect cube.

(iii) 792
792 – 1 = 791
791 – 7 = 784
784 – 19 = 765
765 – 37 = 728
728 – 61 = 667
667 – 91 = 576
576 – 127 = 449
449 – 169 = 280
∴ We see 280 is left as 280 <217
∴ 792 is not a perfect cube.

(iv) 1331
1331 – 1 = 1330
1330 -7 = 1323
1323 – 19 = 1304
1304 – 37 = 1267
1267 – 61 = 1206
1206 – 91 = 1115
1115 – 127 = 988
988 – 169 = 819
819 – 217 = 602
602 – 271 = 331
331 – 331 =0
∴ 1331 is a perfect cube

Question 3.
Find the smallest number that must be subtracted from those of the numbers in question 2, which are not perfect cubes, to make them perfect cubes. What are the corresponding cube roots ?
Solution:
We have examined in Question 2, the numbers 130, 345 and 792 are not perfect cubes. Therefore
(i) 130
130 – 1 = 129
129 -7= 122
122 -19 = 103
103 – 37 = 66
66 – 61 = 5
Here 5 is left
∴ 5 < 91 5 is to be subtracted to get a perfect cube.
Cube root of 130 – 5 = 125 is 5

(ii) 345
345 – 1 = 344
344 -7 = 337
337 – 19 = 318
318 – 37 = 281
281 – 61 =220
220 – 91 = 129
129 – 127 = 2
Here 2 is left ∵ 2 < 169
∴ Cube root of 345 – 2 = 343 is 7
∴ 2 is to be subtracted to get a perfect cube.

(iii) 792
792 – 1 = 791
791 – 7 = 784
784 – 19 = 765
765 – 37 = 728
728 – 61 =667
667 – 91 = 576 5
76 – 127 = 449
449 – 169 = 280
280 – 217 = 63
∴ 63 <217
∴ 63 is to be subtracted
∴ Cube root of 792 – 63 = 729 is 9

Question 4.
Find the cube root of each of the following natural numbers :
(i) 343
(ii) 2744
(iii) 4913
(iv) 1728
(v) 35937
(vi) 17576
(vii) 134217728
(viii) 48228544
(ix) 74088000
(x) 157464
(xi) 1157625
(xii) 33698267
Solution:

Question 5.
Find the smallest number which when multiplied with 3600 will make the product a perfect cube. Further, find the cube root of the product.
Solution:

Grouping the factors in triplets of equal factors, we see that 2, 3 x 3 and 5 x 5 are left
∴ In order to complete the triplets, we have to multiply it by 2, 3 and 5.
∴ The smallest number to be multiplied = 2×2 x 3 x 5 = 60
Now product = 3600 x 60 = 216000 and cube root of 216000

Question 6.
Multiply 210125 by the smallest number so that the product is a perfect cube. Also, find out the cube root of the product.
Solution:

Grouping the factors in triplets of equal factors, we see that 41 x 41 is left
∴ In order to complete the triplet, we have to multiply it by 41
∴ Smallest number to be multiplied = 41
∴ Product = 210125 x 41 = 8615125
∴ Cube root of 8615125

Question 7.
What is the smallest number by which 8192 must be divided so that quotient is a perfect cube ? Also, find the cube root of the quotient so obtained.
Solution:

Grouping the factors in triplets of equal factors, we see that 2 is left
∴ Dividing by 2, we get the quotient a perfect cube
∴ Perfect cube = 8192 + 2 = 4096

Question 8.
Three numbers are in the ratio 1:2:3. The sum of their cubes is 98784. Find the numbers.
Solution:
Ratio in numbers =1:2:3
Let first number = x
Then second number = 2x
and third number = 3x
∴ Sum of cubes of there numbers = (x)³ + (2x)³+(3x)³

Question 9.
The volume of a cube is 9261000 m³. Find the side of the cube.
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
The following numbers are not perfect squares. Give reason :
(i) 1547
(ii) 45743
(iii) 8948
(iv) 333333

Solution:
We know that if the units digit is 2, 3, 7 or 8 of a number, then the number is not a perfect square.

(i) ∴ 1547 has 7 as units digit.
∴ It is not a perfect square.

(ii) 45743 has 3 as units digit
∴ It is not a perfect square.

(iii)  ∴ 8948 has 8 as units digit
∴ It is not a perfect square.

(iv)  ∴ 333333 has 3 as units digits
∴ It is not a perfect square.

Question 2.
Show that the following numbers are not perfect squares :
(i) 9327
(ii) 4058
(iii) 22453
(iv) 743522

Solution:
(i) 9327
∴ The units digit of 9327 is 7
∴ This number can’t be a perfect square.

(ii) 4058
∴ The units digit of 4058 is 8
∴ This number can’t be a perfect square.

(iii) 22453
∴ The units digit of 22453 is 3
.∴ This number can’t be a perfect square.

(iv) 743522
∴ The units digit of 743522 is 2
∴ This number can’t be a perfect square.

Question 3.
The square of which of the following numbers would be an odd number ?
(i) 731
(ii) 3456
(iii) 5559
(iv) 42008
Solution:
We know that the square of an odd number is odd and of even number is even. Therefore
(i) Square of 731 would be odd as it is an odd number.
(ii) Square of 3456 should be even as it is an even number.
(iii) Square of 5559 would be odd as it is an odd number.
(iv) The square of 42008 would be an even number as it is an even number.
Therefore suqares of (i) 731 and (ii) 5559 will be odd numbers.

Question 4.
What will be the units digit of the squares of the following numbers ?
(i) 52
(ii) 977
(iii) 4583
(iv) 78367
(v) 52698
(vi) 99880
(vii) 12796
(viii) 55555
(ix) 53924

Solution:

(i) Square of 52 will be 2704 or (2)² = 4
∴ Its units digit is 4.

(ii) Square of 977 will be 954529 or (7)² = 49 .
∴ Its units digit is 9

(iii) Square of 4583 will be 21003889 or (3)² = 9
∴ Its units digit is 9

(iv) IS 78367, square of 7 = 7² = 49
∴ Its units digit is 9

(v) In 52698, square of 8 = (8)² = 64
∴ Its units digit is 4

(vi) In 99880, square of 0 = 0² = 0
∴ Its units digit is 0

(vii) In 12796, square of 6 = 6² = 36
∴ Its units digit is 6

(viii) In In 55555, square of 5 = 5² = 25
∴ Its units digit is 5

(ix) In 53924, square pf 4 = 4² = 16
∴ Its units digit is 6

Question 5.
Observe the following pattern
1 + 3 = 2²
1 + 3 + 5 = 3²
1+34-5 + 7 = 4²
and write the value of 1 + 3 + 5 + 7 + 9 +…………upto n terms.
Solution:
The given pattern is
1 + 3 = 2²
1 + 3 + 5 = 3²
1+3 + 5 + 7 = 4²
1+3 + 5 + 7 + 9 +……………… upto n terms (number of terms)² = n²

Question 6.
Observe the following pattern :
2² – 1² = 2 + 1
3² – 2² = 3 + 2
4² – 3² = 4 + 3
5² – 4² = 5 + 4
Find the value of
(i) 100² – 99²
(ii) 111² – 109²
(iii) 99² – 96²
Solution:
From the given pattern,
2² – 1² = 2 + 1
3² – 2² = 3 + 2
4² – 3² = 4 + 3
₅² – 4² = 5 + 4
Therefore
(i) 100²-99° = 100 + 99

(ii) 111² – 109² = 111² – 110²– 109²
= (111² – 110²) + (110² – 109²)
= (111 + 110) + (110+ 109)
= 221 + 219 = 440

(iii) 99² – 96² = 99² – 98² + 98² – 97² + 97² – 96²
= (99² – 98²) + (98² – 97²) + (97² – 96²)
= (99 + 98) + (98 + 97) + (97 + 96)
= 197 + 195 + 193 = 585

Question 7.
Which of the following triplets are Pythagorean ?
(i) (8, 15, 17)
(ii) (18, 80, 82)
(iii) (14, 48, 51)
(iv) (10, 24, 26)
(vi) (16, 63, 65)
(vii) (12, 35, 38)
Solution:
A pythagorean triplet is possible if (greatest number)² = (sum of the two smaller numbers)

(i) 8, 15, 17
Here, greatest number =17
∴ (17)² = 289
and (8)² + (15)² = 64 + 225 = 289
∴ 8² + 152 = 172
∴ 8, 15, 17 is a pythagorean triplet

(ii) 18, 80, 82
Greatest number = 82
∴ (82)² = 6724
and 18² + 80² = 324 + 6400 = 6724
∴ 18² + 80² = 82²
∴ 18, 80, 82 is a pythagorean triplet

(iii) 14, 48, 51
Greatest number = 51
∴ (51)² = 2601
and 14² + 48² = 196 + 2304 = 25 00
∴ 51²≠ 14² + 48²
∴ 14, 48, 51 is not a pythagorean triplet

(iv) 10, 24, 26
Greatest number is 26
∴ 26² = 676
and 102 + 242 = 100 + 576 = 676
∴ 26² = 10² + 24²
∴ 10, 24, 26 is a pythagorean triplet

(vi) 16, 63, 65
Greatest number = 65
∴ 65² = 4225
and 16² + 63² = 256 + 3969 = 4225
∴ 65² = 16² + 63²
∴ 16, 63, 65 is a pythagorean triplet

(vii) 12, 35, 38
Greatest number = 38
∴ 38² = 1444
and 12² + 35² = 144 + 1225 = 1369
∴ 38² ≠12² + 35²
∴ 12, 35, 38 is not a pythagorean triplet.

Question 8.
Observe the following pattern

Solution:
From the given pattern

Question 9.
Observe the following pattern

and find the values of each of the following :
(i) 1 + 2 + 3 + 4 + 5 +….. + 50
(ii) 31 + 32 +… + 50
Solution:
From the given pattern,

Question 10.
Observe the following pattern

and find the values of each of the following :
(i) 1² + 2² + 3² + 4² +…………… + 10²
(ii) 5² + 6² + 7² + 8² + 9² + 10² + 12²
Solution:
From the given pattern,

Question 11.
Which of the following numbers are squares of even numbers ?
121,225,256,324,1296,6561,5476,4489, 373758
Solution:
We know that squares of even numbers is also are even number. Therefore numbers 256, 324,1296, 5476 and 373758 have their units digit an even number.
∴ These are the squares of even numbers.

Question 12.
By just examining the units digits, can you tell which of the following cannot be whole squares ?

1. 1026
2. 1028
3. 1024 
4. 1022
5. 1023
6. 1027

Solution:
We know that a perfect square cam at ends with the digit 2, 3, 7, or 8
∴ By examining the given number, we can say that 1028, 1022, 1023, 1027 can not be perfect squares.

Question 13.
Write five numbers for which you cannot decide whether they are squares.
Solution:
A number which ends with 1,4, 5, 6, 9 or 0
can’t be a perfect square
2036, 4225, 4881, 5764, 3349, 6400

Question 14.
Write five numbers which you cannot decide whether they are square just by looking at the unit’s digit.
Solution:
A number which does not end with 2, 3, 7 or 8 can be a perfect square
∴ The five numbers can be 2024, 3036, 4069, 3021, 4900

Question 15.
Write true (T) or false (F) for the following statements.
(i) The number of digits in a square number is even.
(ii) The square of a prime number is prime.
(iii) The sum of two square numbers is a square number.
(iv) The difference of two square numbers is a square number.
(vi) The product of two square numbers is a square number.
(vii) No square number is negative.
(viii) There is not square number between 50 and 60.
(ix) There are fourteen square number upto 200. 

Solution:
(i) False : In a square number, there is no condition of even or odd digits.
(ii) False : A square of a prime is not a prime.
(iii) False : It is not necessarily.
(iv) False : It is not necessarily.
(vi) True.
(vii) True : A square is always positive.
(viii) True : As 7² = 49, and 8² = 64.
(ix) True : As squares upto 200 are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 which are fourteen in numbers.

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
Find the square root of each of the long division method.
(I) 12544
(ii) 97344
(iii) 286225
(iv) 390625
(v) 363609
(vi) 974169
(vii) 120409
(viii) 1471369
(ix) 291600
(x) 9653449
(xi) 1745041
(xii) 4008004
(xiii) 20657025
(xiv) 152547201
(jcv) 20421361
(xvi) 62504836
(xvii) 82264900
(xviii) 3226694416
(xix)6407522209
(xx) 3915380329
Solution:
<

Question 2.
Find the least number which must be subtracted from the following numbers to make them a perfect square :
(i) 2361
(ii) 194491
(iii) 26535
(iv) 16160
(v) 4401624
Solution:
(i) 2361
Finding the square root of 2361

We get 48 as quotient and remainder = 57
∴ To make it a perfect square, we have to subtract 57 from 2361
∴ Least number to be subtracted = 57
(ii) 194491
Finding the square root of 194491

We get 441 as quotient and remainder = 10
∴ To make it a perfect square, we have to subtract 10 from 194491
∴ Least number to be subtracted = 10
(iii) 26535
Finding the square root of 26535

We get 162 as quotient and 291 as remainder
∴ To make it a perfect square, we have to subtract 291 from 26535
∴ Least number to be subtracted = 291
(iv)16160
Finding the square root of 16160

We get 127 as quotient and 31 as remainder
∴ To make it a perfect square, we have to subtract 31 from 16160
∴ Least number to be subtracted = 31
(v) 4401624
Find the square root of 4401624

We get 2098 as quotient and 20 as remainder
∴ To make it a perfect square, we have to subtract 20 from 4401624
∴ Least number to be subtracted = 20

Question 3.
Find the least number which must be added to the following numbers to make them a perfect square :
(i) 5607
(ii) 4931
(iii) 4515600
(iv) 37460
(v) 506900
Solution:
(i) 5607

Finding the square root of 5607, we see that 74² = 5607- 131 =5476 and 75² = 5625
∴ 5476 < 5607 < 5625
∴ 5625 – 5607 = 18 is to be added to get a perfect square
∴ Least number to be added = 18
(ii) 4931

Finding the square root of 4931, we see that 70²= 4900
∴ 71² = 5041 4900 <4931 <5041
∴ 5041 – 4931 = 110 is to be added to get a perfect square.
∴ Least number to be added =110
(iii) 4515600

Finding the square root of 4515600, we see
that 2124² = 4511376
and 2 1 25² = 45 1 56 25
∴ 4511376 <4515600 <4515625
∴ 4515625 – 4515600 = 25 is to be added to get a perfect square.
∴ Least number to be added = 25
(iv) 37460

Finding the square root of 37460
that 193² = 37249, 194² = =37636
∴ 37249 < 37460 < 37636
∴ 37636 – 37460 = 176 is to be added to get a perfect square.
∴ Least number to be added =176
(v) 506900

Finding the square root of 506900, we see that
711² = 505521, 712² = 506944
∴ 505521 < 506900 < 506944
∴ 506944 – 506900 = 44 is to be added to get a perfect square.
∴ Least number to be added = 44

Question 4.
Find the greatest number of 5 digits which is a perfect square.
Solution:
Greatest number of 5-digits = 99999 Finding square root, we see that 143 is left as remainder

∴ Perfect square = 99999 – 143 = 99856 If we add 1 to 99999, it will because a number of 6 digits
∴ Greatest square 5-digits perfect square = 99856

Question 5.
Find the least number of four digits which is a perfect square.
Solution:
Least number of 4-digits = 10000
Finding square root of 1000
We see that if we subtract 39

From 1000, we get three digit number
∴ We shall add 124 – 100 = 24 to 1000 to get a
perfect square of 4-digit number
∴ 1000 + 24 = 1024
∴ Least number of 4-digits which is a perfect square = 1024

Question 6.
Find the least number of six-digits which is a perfect square.
Solution:
Least number of 6-digits = 100000

Finding the square root of 100000, we see that if we subtract 544, we get a perfect square of 5-digits.
So we shall add
4389 – 3900 = 489
to 100000 to get a perfect square
Past perfect square of six digits= 100000 + 489 =100489

Question 7.
Find the greatest number of 4-digits which is a perfect square.
Solution:
Greatest number of 4-digits = 9999

Finding the square root, we see that 198 has been left as remainder
∴ 4-digit greatest perfect square = 9999 – 198 = 9801

Question 8.
A General arranges his soldiers in rows to form a perfect square. He finds that in doing so, 60 soldiers are left out. If the total number of soldiers be 8160, find the number of soldiers in each row.
Solution:
Total number of soldiers = 8160 Soldiers left after arranging them in a square = 60
∴ Number of soldiers which are standing in a square = 8160 – 60 = 8100

Question 9.
The area of a square field is 60025 m². A man cycle along its boundry at 18 km/hr. In how much time will be return at the starting point.
Solution:
Area of a square field = 60025 m²

Question 10.
The cost of levelling and turfing a square lawn at Rs. 250 per m² is Rs. 13322.50. Find the cost of fencing it at Rs. 5 per metre ?
Solution:
Cost of levelling a square field = Rs. 13322.50
Rate of levelling = Rs. 2.50 per m²

and perimeter = 4a = 4 x 73 = 292 m Rate of fencing the field = Rs. 5 per m
∴ Total cost of fencing = Rs. 5 x 292 = Rs. 1460

Question 11.
Find the greatest number of three digits which is a perfect square.
Solution:
3-digits greatest number = 999

Finding the square root, we see that 38 has been left
∴ Perfect square = 999 – 38 = 961
∴ Greatest 3-digit perfect square = 961

Question 12.
Find the smallest number which must be added to 2300 so that it becomes a perfect square.
Solution:
Finding the square root of 2300

We see that we have to add 704 – 700 = 4 to 2300 in order to get a perfect square
∴ Smallest number to be added = 4

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Using square root table, find the square roots of the following :

Question 1.
7
Solution:

Question 2.
15
Solution:

Question 3.
74
Solution:

Question 4.
82
Solution:

Question 5.
198
Solution:

Question 6.
540
Solution:

Question 7.
8700
Solution:

Question 8.
3509
Solution:

Question 9.
6929
Solution:

Question 10.
25725
Solution:

Question 11.
1312
Solution:

Question 12.
4192
Solution:

Question 13.
4955
Solution:

Question 14.
\(\frac {99 }{ 144 }\)
Solution:

Question 15.
\(\frac {57 }{ 169 }\)
Solution:

Question 16.
\(\frac {101 }{ 169 }\)
Solution:

Question 17.
13.21
Solution:

Question 18.
21.97
Solution:

Question 19.
110
Solution:

Question 20.
1110
Solution:

Question 21.
11.11
Solution:

Question 22.
The area of a square field is 325 m². Find the approximate length of one side of the field.
Solution:

Question 23.
Find the length of a side of a square, whose area is equal to the area bf the rectangle with sides 240 m and 70 m.
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
Write the possible unit’s digits of the square root of the following numbers. Which of these numbers are odd square roots ?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i)  In \(\sqrt { 9801 }\) ∴ the units digits is 1, therefore, the units digit of the square root can be 1 or 9
(ii) In \(\sqrt { 799356 }\) ∴ the units digit is 6
∴ The units digit of the square root can be 4 or 6
(iii) In \(\sqrt { 7998001 }\) ∴ the units digit is 1
∴ The units digit of the square root can be 1 or 9
(iv) In 657666025
∴ The unit digit is 5
∴ The units digit of the square root can be 5

Question 2.
Find the square root of each of the following by prime factorization.
(i) 441
(ii) 196
(iii) 529
(iv) 1764
(v) 1156
(vi) 4096
(vii) 7056
(viii) 8281
(ix) 11664
(x) 47089
(xi) 24336
(xii) 190969
(xiii) 586756
(xiv) 27225
(xv) 3013696
Solution:

Question 3.
Find the smallest number by which 180 must be multiplied so that it becomes a perfect square. Also, find the square root of the perfect square so obtained.
Solution:
Factorising 180,

180 = 2 x 2 x 3 x 3 x 5
Grouping the factors in pairs we see that factor 5 is left unpaired.
∴ Multiply 180 by 5, we get the product 180 x 5 = 900
Which is a perfect square
and square root of 900 = 2 x 3 x 5 = 30

Question 4.
Find the smallest number by which 147 must be multiplied so that it becomes a perfect square. Also, find the square root of the number so obtained.
Solution:
Factorising 147,

147 = 3 x 7×7
Grouping the factors in pairs of the equal factors, we see that one factor 3 is left unpaired
∴ Multiplying 147 by 3, we get the product 147 x 3 = 441
Which is a perfect square
and its square root = 3×7 = 21

Question 5.
Find the smallest number by which 3645 must be divided so that it becomes a perfect square. Also, find the square root of the resulting number.
Solution:
Factorising 3645

3645 = 3 x 3 3 x 3 x 3 x 3 x 5
Grouping the factors in pair of the equal factors, we see t at one factor 5 is left unpaired
∴ Dividing 3645 by 5, the quotient 729 will be the perfect square and square root of 729 = 27

Question 6.
Find the smallest number by which 1152 must be divided so that it becomes a perfect square. Also, find the square root of the number so obtained.
Solution:
Factorsing 1152,

1152 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
Grouping the factors in pairs of the equal factors, we see that factor 2 is left unpaired.
∴ Dividing by 2, the quotient 576 is a perfect square .
∴ Square root of 576, it is 24

Question 7.
The product of two numbers is 1296. If one number is 16 times the others find the numbers.
Solution:
Product of two numbers = 1296
Let one number = x
Second number = 16x

∴ First number = 9
and second number = 16 x 9 = 144

Question 8.
A welfare association collected Rs. 202500 as donation from the residents. If each paid as many rupees as there were residents find the number of residents.
Solution:
Total donation collected = Rs. 202500
Let number of residents = x
Then donation given by each resident = Rs. x
∴ Total collection = Rs. x x x

Question 9.
A society collected Rs. 92.16. Each member collected as many paise as there were members. How many members were there and how much did each contribute?
Solution:
Total amount collected = Rs. 92.16 = 9216 paise
Let the number of members = x
Then amount collected by each member = x
paise

∴ Number of members = 96
and each member collected = 96 paise

Question 10.
A school collected Rs. 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school ?
Solution:
Total fee collected = Rs. 2304
Let number of students = x
Then fee paid by each student = Rs. x
∴ x x x = 2304 => x² = 2304
∴ x = \(\sqrt { 2304 }\)

Question 11.
The area of a square field is 5184 m². A rectangular field, whose length is twice its breadth has its perimeter equal to the perimeter of the square field. Find the area of the rectangular field.
Solution:
The area of a square field = 5184 m²
Let side of the square = x

∴ side of square= 72 m
∴ Perimeter, of square field = 72 x 4 m = 288 m
Perimeter of rectangle = 288 m
Let breadth of rectangular field (b) = x
Then length (l) = 2x
∴ Perimeter = 2 (l + b)
= 2 (2x + x) = 2 x 3x = 6x
= 2 (2x + x) = 2 x 3x = 6x

∴ Length of rectangular field = 2x = 2 x 48 = 96 m
and breadth = 48 m
and area = l x b = 96 x 48 m²
= 4608 m²

Question 12.
Find the least square number, exactly divisible by each one of the numbers :
(i) 6, 9,15 and 20
(ii) 8,12,15 and 20
Solution:

LCM of 6, 9, 15, 20 = 2 x 3 x 5 x 3 x 2 = 180
=2 x 2 x 3 x 3 x 5
We see that after grouping the factors in pairs, 5 is left unpaired
∴ Least perfect square = 180 x 5 = 900

We see that after grouping the factors,
factors 2, 3, 5 are left unpaired
∴ Perfect square =120 x 2 x 3 x 5 = 120 x 30 = 3600

Question 13.
Find the square roots of 121 and 169 by the method of repeated subtraction.
Solution:

Question 14.
Write the prime factorization of the following numbers and hence find their square roots. ^
(i) 7744
(ii) 9604
(iii) 5929
(iv) 7056
Solution:
Factorization, we get:
(i) 7744 = 2 x 2 x 2 x 2 x 2 x 2 x 11 x 11

Grouping the factors in pairs of equal factors,

Question 15.
The students of class VIII of a school donated Rs. 2401 for PM’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Total amount of donation = 2401
Let number of students in VIII = x
∴ Amount donoted by each student = Rs. x

Question 16.
A PT teacher wants to arrange maximum possible number of 6000 students in a Held such that the number of rows is equal to the number of columns. Find the number of rows if 71 were left out after arrangement.
Solution:
Number of students = 6000
Students left out = 71
∴ Students arranged in a field = 6000 – 71=5929

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.