Category: CBSE Class 9

On this page, you will find Sound Class 9 Notes Science Chapter 12 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 12 Sound will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 12 Notes Sound

Sound Class 9 Notes Understanding the Lesson

1. Sound
Sound is a form of energy which produces a sensation of hearing in our ears.

2. Production of sound
Sound is produced by vibration of objects.

• The sound of human voice is produced due to vibration in the vocal chord.

3. Propagation of sound
Sound propagates in the form of longitudinal waves and these waves require material medium to propagate. Hence sound waves are mechanical waves.

• A wave is a disturbance that moves through a medium when the particles of the medium set neighbouring particles into motion.
• The longitudinal wave of sound travels in the form of compression and rarefaction. Compression is the region of high pressure and rarefaction is the region of low pressure.
• The propagation of sound can be visualised as propagation of density variations or pressure variation in the medium.

4. Sound needs a medium to travel
Sound is a mechanical wave and need a material medium for its propagation.

• Longitudinal wave
  A wave in which the particles of the medium oscillate to and fro in the same direction in which the wave is moving is called longitudinal wave.
• Transversal wave
  A wave motion is said to transverse if the particles of the medium through which the wave propagates vibrate in the direction perpendicular to the direction of propagation of the wave.

5. Some important terms and Relations for longitudinal wave
Frequency: The frequency of wave is defined as the number of waves produced per second.
Or
The frequency of a sound wave is defined as the number of complete oscillations made by the particle of medium in one second.

• It is denoted by greek letter u (nu). Its SI unit is hertz (Hz).

(ii) Wavelength: The distance between two consecutive compressions or two consecutive rarefactions is called wavelength.

• It is usually represented by X (Greek letter lambda). Its SI units is metre (m).

(iii) Time period: The time taken by two consecutive compressions or rarefactions to cross a fixed point is called time period of wave.
Or

• Time taken by particle of medium to complete one oscillation is known as time period.
• It is represented by the symbol T. Its SI unit is second (s).

8. Amplitude: The magnitude of the maximum disturbance in the medium on either side of the mean value is called amplitude of wave. It is usually represented by the letter A. For sound its unit will be that of density or pressure.

9. Speed: The speed of sound is defined as the distance which a point on a wave, such as a compression or a rarefraction, travels per unit time.

10. Relations

• Relation between time period (T) and frequency (u)
  \(T=\frac{1}{v}\)
• Relation between speed of wave (υ), wavelength (λ) time period (T) and frequency (υ)
  υ = υλ

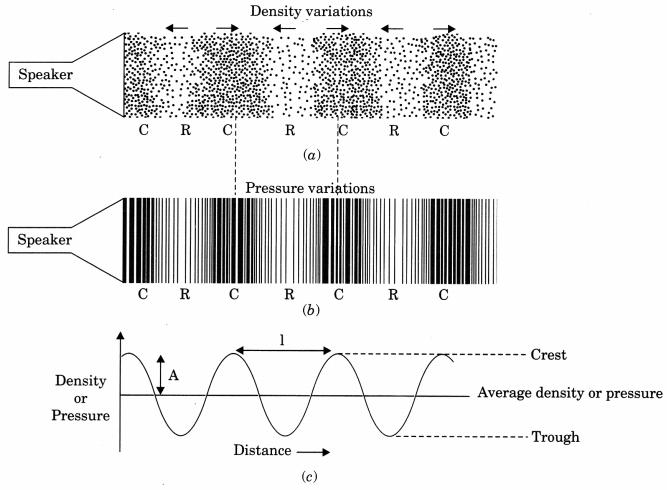
Sound propagates as density or pressure variations as shown in (a), (b) and (c) represents graphically the density and pressure variations.

11. Characteristics of a sound wave
We can describe a sound wave by

• Frequency
• Amplitude
• Speed

12. Frequency-pitch:

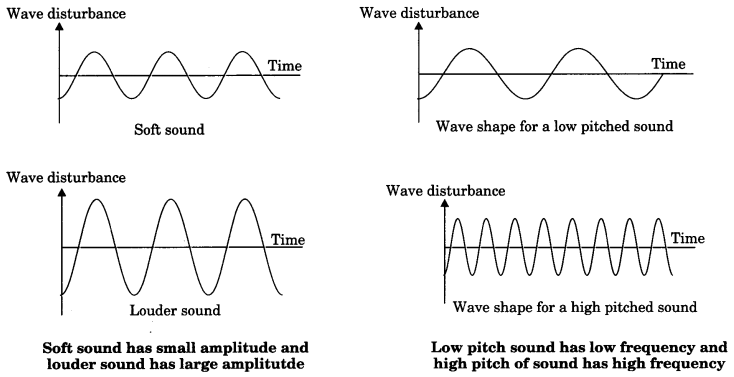
• How the brain interprets the frequency of an emitted sound is called its pitch. The faster the vibration of the source, the higher is the frequency and the higher is the pitch.
• The pitch of sound produced by an object of low frequency is low and the source described as flat sound.
• The pitch of sound produced by an object vibrating with high frequency is high and the sound is described as shrill sound.

13. Amplitude-loudness:

• The loudness or softness of a sound is determined by its amplitude. Greater the amplitude of vibration of source, greater is the loudness of sound.
• Loud sound can travel a larger distance as it is associated with high energy.
• A sound wave moves away from the source, its amplitude as well as its loudness decreases.

14. Quality-timber:

• The quality or timber of sound is that characteristics which enables us to distinguish one sound from an¬other having same loudness and pitch.
• A sound of single frequency is called a tone. The sound which is produced due to a mixture of several fre¬quencies is called a note and is pleasant to listen to.
• Quality of sound is represented by waveform.
• Noice is unpleasant to ear. Music is pleasant to hear and is of rich quantity.

15. Speed of sound in different media

• Speed of sound in a medium depends on inertia and elasticity of the medium.
• Speed of sound increases with increase in temperature.
• The speed of sound decreases when we go from solid to gaseous state.
  Speed of sound in solids > Speed of sound in liquids > Speed of sound in gases
• Speed of sound in air is 331 ms-1 at 0°C and 344 ms^-1 at 22°C.

16. Reflection of sound
Sound is reflected in same way as light. Incident and reflected ray make equal angles with the normal to the reflecting surface at the point of incidence and three are in the same plane.

17. Echo
An echo is the phenomenon of repetition of sound by reflection from an obstacle.

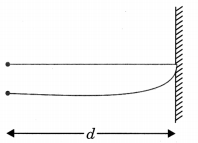
• The sensation of sound lasts in brain for (1/10) of a second. This property is called persistence of hearing. To hear a distinct echo the time interval between the original sound and the reflected one must be at least
  0. 1 second.
• For hearing a distinct echo, the minimum distance of the obstacle from the source of sound should be 17.2 m.

Take speed of sound = 344 m/s
(at temperature 20°C)
2d = v x t
v = 344 m/s
\(t=\frac{1}{10} \mathrm{s}\)
d=17.2m

18. Reverberation
A sound created in a big hall will persist by repeated reflection from the walls until it is reduced to a value where it is no longer audible. The repeated reflection that results in the persistence of sound is called reveberation.

Excessive reveberation is highly undesirable. To reduce reverberation, the roof and walls of the auditorium are generally covered with sound absorbent materials like compressed fibre board, rough plaster or draperies. The seat materials are also selected on the basis of their sound absorbing properties.

Reflection of sound
d – distance of person from obstacle
v = velocity of sound
t = time after echo is heard
2d = v x t
t = 2 dlv and d = vt/2

19. Uses of multiple reflection of sound
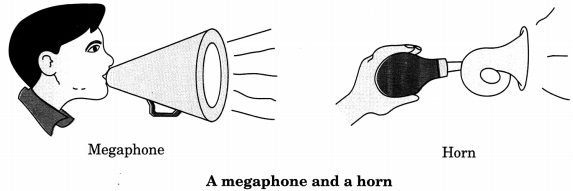
(i) Megaphones, horns, musical instruments such as trumpets and shehnais are all designed to send sound in a particular direction. In these instruments, a tube followed by a conical opening reflects sound successively to guide most of sound successively to guide most of sound from the source in the forward direction towards the audience.

2. Stethoscope is a medical instrument used for listening to sounds produced within the body, chiefly in the heart or lungs

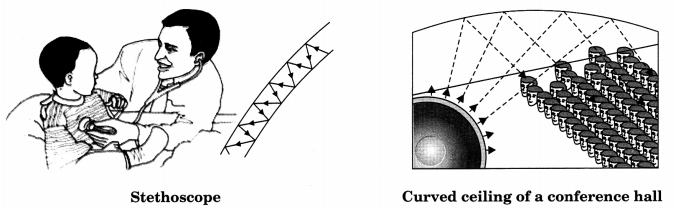
In stethoscopes the sound of the patient’s heartbeat reaches the doctor’s ears by multiple reflection of sound.

3. Generally the ceiling of concert halls, conference halls and cinema halls are curved so that sound after reflection reaches all corners of the hall.
Sometimes curved sound board may be placed behind of the stage so that the sound after reflecting from the sound board, spreads evenly across the width of the hall.

20. Range of Hearing

• Audible range: The sound whose frequency lies between 20 Hz and 20,000 Hz which we are able to hear is called audible sound.
  Inaudible range
• Infrasonic sound: Sound of frequencies below 20 Hz is called infrasonic sound or infra sound.
• Ultrasonic sound: Frequency higher than 20 KHz is called ultrasonic sound or ultrasound.

21. Uses of Ultrasound in Communication
Sonar
The acronym sonar stands for sound navigation and ranging.
Sonar is a device that uses ultrasonic waves to measure the distance, direction and speed of underwater objects.

22. Components of sonar system
Sonar consists of a transmitter and a detector and is installed in a boat or a ship.

23. Working
The transmitter produces and transmits ultrasound waves. These waves travel through water and after striking the object on the sea bed, get reflected back and are sensed by the detector. The detector converts the ultrasonic waves into electrical signals which are appropriately interpreted.

24. Calculation of distance : The distance of the object that reflected the sound wave can be calculated by knowing the speed of sound in water and the time interval between transmission and reception of the ultrasound

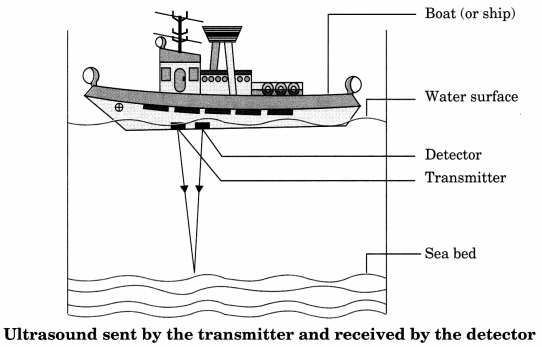
Let the time intervel between transmission and reception of ultrasound signal be t and speed of sound through sea water be υ. The total distance, 2d, travelled by the ultrasound.

• Rhinoceroses communicate using infra sound of frequency as low as 5 Hz.
• Whales and elephants produce sound in infrasonic wave.
• Children under five and some animals, such as dogs can hear infrasonic sound.

Earthquake produces infrasonic waves.

• Ultrasound is produced by dolphines, bats and porpoises. R
• Moths of certain families can hear high frequency waves.

25. Application of Ultrasound
Industrial uses of ultrasound

(i) Cleaning instruments and electronic components
Ultrasound is generally used to clean parts located in hard to reach places, for example, spiral tube, odd shaped parts, electronic component, etc. Objects to be cleaned are placed in a cleaning solution and ultrasonic waves are sent into the solution. Due to the high frequency, the particles of dust, grease and dirt get detached and drop out. The objects are thus thoroughly cleaned.

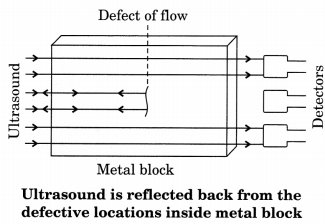
(ii) Detecting flaw and cracks in metal blocks
Ultrasounds can be used to detect crack and flaws in metal blocks. Metallic components are generally used in the construction of big structures like buildings, bridges, machines and also scientific equipments. The cracks or holes inside the metal blocks, which are invisible from outside reduces the strength of the structure. Ultrasonic waves are allowed to pass through the metal block and detectors are used to detect the transmitted waves. If there is even a small defect, the ultrasound gets reflected back indicating the presence of flaws or defect.

Medical uses of ultrasound
(i) Ultrasonography: The technique of obtaining of images of internal organs of the body by using ultrasonic waves is called ultrasonography. An ultrasound scanner is a medical instrument which is used by doctors to detect abnormalities such as stones in gall bladder and kidney or tumours in different organs. In this technique, the ultrasound scanner produces ultrasounds which travel through the tissues of the body, and if there are stones in the gall bladder or kidney or there is tumour in any internal organ, then the ultrasound waves get reflected from these regions due to the change in tissue density. These reflected ultrasound waves are converted into electrical signals and fed to the computer generating a three dimension images of the organ on the monitor of the computer.

(ii) Echocardiography: The technique of obtaining images of the heart by using reflection of ultrasonic waves from various parts of the heart is called echocardiography.

(iii) Breaking of kidney stones: Ultrasound can be used to break small stones formed in the kidney into fine grains. These grains later get flushed out of with urine.
2d = v x t

(iv) Use of ultrasound by bats for determining distance
Bats search out prey and fly in dark night by emitting and detecting reflections of ultrasonic waves. The high pitched ultrasonic squeaks of the bat are reflected from the obstacles or prey and returned to bat’s ear. The nature of reflection tells the bat where the obstacle or pray is and what it is like.

26. Structure of the Human Ear
Introduction
The outer ear is called ‘pinna’. It collects the sound from the surroundings. The collected sound passes through the auditory canal. At the end of the auditory canal there is a thin membrane called the eardrum or tympanic membrane. When compression of the medium reaches the eardrum the pressure on the outside of the membrane increases and forces the eardrum inward.

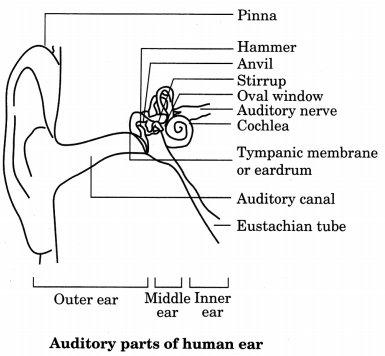
Similarly, the eardrum moves outward when a rarefraction reaches it. In this way the eardrum vibrates. The vibrations are amplified several times by three bones (the hammer, anvil and stirrup) in the middle ear. The middle ear transmits the amplified pressure variations received from the sound wave to the inner ear. In the inner ear, the pressure variations are turned into electrical signals by the cochlea. These electrical signals are sent to the brain via the auditory nerve, and the brain interprets them as sound.

Parts	Function
1. Pinna	Collects sound from surroundings
2. Hammer, anvil and stirrup	Amplifies vibration or pressure wave
3. Cochlea	Converts pressure variation into electrical signal
4. Eardrum	Thin membrane vibrates when sound reaches inside ear
5. Auditory nerve	Electrical signals are sent to brain from cochlea via auditory nerve.

Class 9 Science Chapter 12 Notes Important Terms

Sound: Sound is a form of energy which produces a sensation of hearing in our ears.

Longitudinal wave: A wave in which the particles of the medium oscillate to and fro in the same direction in which the wave is moving is called longitudinal wave.

Transverse wave: A wave in which particles of the medium vibrate at right angles to the direction of the propagation of the the wave.

Echo: The repetition of sound caused by the reflection of sound waves is called an echo.

Reverberation: The persistence of sound in a big hall due to repeated reflection of sound from the walls, ceiling and floor of the hall is called reverberation.

Stethoscope: Stethoscope is a medical instrument used for listening to sounds produced within the body, chiefly in the heart or lungs.

Sonar: Sonar is a device that uses ultrasonic wave to measure the distance, direction and speed of underwater object.

ultrasonography: The technique of obtaining images of internal organs of the body by using echoes of ultrasound wave is called ultrasonography.

Echo cardiography: The technique of obtaining images of the heart by using reflection of ultrasonic waves from various parts of the heart is called echo cardiography.

On this page, you will find Work, Power And Energy Class 9 Notes Science Chapter 11 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 11 Work, Power And Energy will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 11 Notes Work, Power And Energy

Work, Power And Energy Class 9 Notes Understanding the Lesson

1. Work done by a constant force
Work done by a force acting on an object is equal to the magnitude of the force multiplied by the distance moved in the direction of the force.
Work done = force x displacement

• Work done has only magnitude and no direction i.e., work is a scalar quantity.
• SI unit of work is joule (J).
• 1 joule (one joule)

W = Fs
If F = 1 N and s = 1 m
W= 1 N x 1 Nm
W =  1 Nm
1j =1 Nm
1 J is the amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.

2. Conditions that need to be satisfied for work to be done

• Force should act on an object.
• The object must be displaced.

3. Zero work, Positive and Negative work
(i) Zero work: If the angle between force and displacement is 90°, then work done is said to be zero work.
Example: When a man carries a load on his hand and moves on a level road, work done by the man on the load is zero.

(ii) Positive work: Work done is said to be positive if force applied on an object and displacement are in the same direction.

Example: Work done by the force of gravity on a falling body is positive.

(iii) Negative work: Work done is said to be negative if the applied force on an object and displacement are in opposite direction.
W = -Fs
Here displacement is taken to be negative (-s).

Example: Work done by friction force is usually negative on a moving body.

4. Energy
Energy of a body is defined as the capacity or ability of a body to do work.
The SI unit of energy is joule (J) (unit of energy and work is same).

5. Forms of energy
There are various forms of energy in the nature, few of them are mechanical energy (potential energy + kinetic energy) heat energy, chemical energy and light energy.

6. Mechanical energy
Mechanical energy includes kinetic energy and potential energy.

7. Kinetic energy
The energy possessed by a body by the virtue of its motion is called kinetic energy.
Kinetic energy possessed by a body can be calculated by
\(E_{K}=\frac{1}{2} m v^{2}\)
m = mass of body
V = velocity of body

8. Derivation of kinetic energy (work energy theorem)
Let us consider an object lying on a frictionless surface having mass ‘m’

A force of constant magnitude F is acting on the body. Here initial velocity of the body is u and final velocity is v. As there is no dissipative forces, work done on the body will be stored in the form of change in kinetic energy.
W=Fs

If the object is starting from a stationary position u = 0, then

9. Potential energy
The energy possessed by a body due to its position or configuration is called potential energy.

10. Gravitational potential energy
Potential energy at any height (h) from a reference can be calculated by formula
E_p = mgh
where, m = mass of object
v = height from reference
The gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity.

11. Derivation of potential energy
When work is done on the body, the work is stored in the form of energy. Consider an object of mass, m. Let it be raised through a height, h from the ground. A force is required to do this. The minimum force required to raise the object is equal to the weight of the object, mg. The object gains energy equal to the work done on it. Let the work done on the object against gravity be W.

That is W = force x displacement
= mgh .
Since work done on the object is equal to mgh, an energy equal to mgh units is gained by the object. This is the potential energy (Ep) of the object.
E_p = mgh

12. Law of conservation of energy
Energy can neither be created nor be destroyed, it can only be transformed from one form to another. The total energy before and after the transformation always remains constant.

13. Transformation of energy in nature
The change of one form of energy into another form of energy is known as transformation of energy.
Example:

• Potential energy of water is converted into electricity in dams.
• Electricity is converted into heat energy in heaters.
• Chemical energy of fuel is converted into mechanical energy in engines.

14. Conservation of mechanical energy
Mechanical energy is the sum of kinetic energy and potential energy.
If there is no loss, then mechanical energy of a system is always constant.
Potential energy + kinetic energy = constant.
or
\(m g h+\frac{1}{2} m v^{2}=\text { constant }\)

15. Power (P)
Power is defined as the rate of doing work or rate of transfer of energy.
Power = work/time
P=W/T

• Unit of power is watt (W).

16. Watt

17. Commercial unit of energy
Kilowatt hour (kWh) or 1 unit
The energy used in households, industries and commercial establishments are usually expressed in kilowatt hour.
1 kWh is the energy used in one hour (1 h) at the rate of 1000 J/s or (1 kW).
∴1 kWh =lkWxU = 1000 W x 3600 s = 3600000 J
1 kWh = 3.6 x 10⁶ J = 1 unit

18. Power can also be represented as,
P = Fv
F = force applied
v = velocity of object
\(P=\frac{W}{t}=\frac{F s}{t}=F v\)

Class 9 Science Chapter 11 Notes Important Terms

Work done: Work done by a force acting on an object is equal to the magnitude of the force multiplied by the distance moved in the direction of the force.

Energy: Energy of a body is defined as the capacity or ability of the body to do work.

Mechanical energy: Mechanical energy of a body is the sum of its kinetic energy and potential energy. Kinetic energy: The energy possessed by a body by the virtue of its motion.

Potential energy: The energy possessed by a body due to its position or configuration.

Law of conservation of energy: Energy can neither be created nor be destroyed, it can only be transformed from one form to another.

Conservation of mechanical energy: If there is no loss of energy, then mechanical energy of a system is always constant.

Power: Power is defined as the rate of doing work or rate of transfer of energy.

Commercial unit of energy: The energy used in households, industries and commercial establishment are usually expressed, in kilowatt hour. 1 kWh = 1 unit = 3.6 x 10⁶

On this page, you will find Gravitation Class 9 Notes Science Chapter 10 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 10 Gravitation will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 10 Notes Gravitation

Gravitation Class 9 Notes Understanding the Lesson

1. Newton’s law of gravitation
“Every particle in the universe attracts every other particle with a force, which is directly proportional to the product of their masses and inversely proportional to the square of the distance between the two masses. The direction of force is along the line joining the two particles.”

Force of attraction between A and B

Where G is constant of proportionality called universal gravitational constant.

2. Universal gravitational constant
\(\mathrm{G}=\frac{\mathrm{F} r^{2}}{m_{1} m_{2}}\)
SI unit of G is Nm² kg^-2
Value of G = 6.67 x 10^-11 Nm² kg^-2.

3. Properties of gravitational force

• It is always attractive in nature.
• It obeys inverse square law  \(\mathrm{F} \alpha \frac{1}{r^{2}}\)
• Gravitational force is independent of the medium.
• It is a long range force.
• It is a weak force.
• Force of gravitation due to the Earth is called gravity.

4. Definition of G
Take = m2 = m = 1 kg r = 1 m
Hence, the force of attraction between two point masses separated by a unit distance is called universal gravitational constant.

5. Importance of the universal law of gravitation:
The universal law of gravitation successfully explained several phenomena

• The force that binds us to the Earth.
• The motion of the moon around the Earth.
• The motion of planets around the Sun; and
• The tides due to the moon and the Sun.

6. Free fall
Whenever objects fall towards the Earth under gravitational force alone, we say that the objects are in free fall.

7. Acceleration due to gravity (g):
The acceleration with which a body falls towards the Earth due to Earth’s gravitational pull is known as acceleration due to gravity. It is denoted by ‘g’.

8. Expression for acceleration due to gravity on the surface of the Earth:
The gravitational force between a body of mass ‘m’ and the Earth (of mass M) can be represented as
\(\mathbf{F}=\frac{\mathrm{G} \mathrm{Mm}}{r^{2}}\) …………….. (1)
Force of gravity is expressed as, F=Mg ……………(2)
From (1) and (2),\(g=\frac{\mathrm{GM}}{r^{2}}\)
The Earth is not a perfect sphere. As the radius of Earth increases from the poles to the equator, the value of g becomes greater at the poles than at the equator.

9. Calculate the value of g on the Earth:
\(g=\frac{G M}{r^{2}}\)
By putting the value of mass, radius of Earth and universal gravitational constant we can find out the value of acceleration due to gravity on the Earth.

10. Acceleration due to gravity at

• the surface of the Earth, g = 9.8 m/s²
• the centre of the Earth, g = 0.

11. Mass
Mass of a body is the quantity of matter contained in it.

• Mass of an object is constant and does not change from place to place.
• SI unit of mass is kilogram (kg).
• Mass of an object is a measure of its inertia.

12. Weight
The weight of an object is the force with which it is attracted towards the Earth.
w = mg

• SI unit of weight is newton (N).
• Weight is a vector quantity.
• Weight is directly proportional to mass of the body. So at a given place, weight of a body is a measure of its mass. w α m.
• Weight of a body changes from place to place because, acceleration due to gravity varies with position and location of a body.

13. Weight of an object on the moon
The acceleration due to gravity of moon is one sixth of Earth.
\(g_{\text {moon }}=\frac{1}{6} g_{\text {Earth }}\)
Due to this, the weight of an object on the moon is one sixth of the weight of the object on the Earth.
\(\frac{\text { Weight of the object on the moon }}{\text { Weight of the object on the Earth }}=\frac{1}{6}\)
Weight of the object on the moon = 1/6 x weight of the object on the Earth.

14. Gravitation (Flotation)
Thrust: The force acting on an object perpendicular to its surface is called thrust.

• SI unit of thrust is newton (N).

Pressure: The thrust on unit area is called pressure.

• SI unit of pressure is N/m² or Nm^-2.
• In honour of scientist Blaise pascal, the SI unit of pressure is called pascal (pa).
  1 pa = 1 N/m²
  Pressure = Thrust/Area

15. Consequences of pressure

(i) Nails and pins have painted ends so that these can be fixed with minimum force because the pressure on the painted ends would be large.

(ii) Wide wooden or metal or concrete sleepers are kept below railway lines to reduce pressure on the railway tracks and prevent them from sinking into the ground.

(iii) The foundation of a building or a dam has a large surface area so that the pressure exerted by it on the ground is less. This is done to prevent the sinking of the building or dam into the ground.

(iv) Skiers use flat skies to slide over snow as the long flat skies increase the area of contact, which reduces pressure exerted by the skier on the snow enabling the skier to slide over the snow without sinking.

(v) Broad handles are provided in bags and suitcases. Due to broad size of the handles, the area of contact increases which reduces the pressure exerted by the weight of the bag or suitcase.

(vi) A camel walks easily on the sandy surface than a man inspite of the fact that a camel is much heavier than a man. This is because their legs are padded and flat which provides greater surface area of contact with the sand and hence exerts less pressure on the sand. On the other hand, a man has very small surface area, so he exerts greater pressure and is likely to sink in sand.

16. Pressure in fluids
A substance which can flow is called a fluid. All liquid and gasses are fluids.

• A fluid contained in a vessel exerts pressure at all points of the vessel and in all directions.
• Pascal’s law: In an enclosed fluid, if pressure is changed in any part of the fluid, then this change in pressure is transmitted undiminished to all the other parts of the fluid.

17. Buoyancy
When a body is partially or wholly immersed in a fluid, an upward force acts on it which is called upthrust or buoyant force. The property of the fluids responsible for this force is called buoyancy.

18. Why do objects float or sink when placed on the surface of a fluid?

1. A body sinks if its weight is greater than the buoyant force acting on it.
Weight > buoyant force
Apparent weight = weight – buoyant force

2. A body floats if buoyant force balance the weight of the body.
A body having an average density greater than that of water (fluid), sinks into it while a body of average density smaller than that of water (fluid), floats on it.

19. Archimedes principle
When a body is immersed fully or partially in a fluid, it experiences an upward force that is equal to the weight of the fluid displaced by it.

20. Density and relative density
Density: Density of a substance is defined as its mass per unit volume.
\(\text { Density }=\frac{\text { Mass }(\mathrm{M})}{\text { Volume }(v)} \text { or, } d=\frac{\mathrm{M}}{\mathrm{V}}\)
SI unit of density is kg/m³ or kg m^-3

21. Relative density: The relative density of a substance is the ratio of its density to that of water.
Relative density = Density of substance/Density of water.
It has no unit.

Class 9 Science Chapter 10 Notes Important Terms

Newton’s law of gravitation: Every particle in the universe attracts every other particle with a force, which is directly proportional to the product of their masses and inversely proportional to square of distance between the two masses.

Freefall: Whenever objects fall towards the Earth under gravitational force alone, we say that the objects are in free fall.

Acceleration due to gravity: The acceleration with which a body falls towards the Earth due to Earth’s gravitational pull is known as acceleration due to gravity.

Mass: Mass of a body is the quantity of matter contained in it.

Weight: The weight of an object is the force with which it is attracted towards the Earth.

Density: Density of a substance is defined as its mass per unit volume.

Relative density: The relative density of a substance is the ratio of its density to that of water.

Thrust: The force acting on an object perpendicular to the surface is called thrust.

Pressure: The thrust per unit area is called pressure.

Pascal’s law: In an enclosed fluid, if pressure is changed in any part of the fluid, then this change in pressure is transmitted undiminished to all the other parts of the fluid.

Buoyancy: When a body is partially or wholly immersed in a fluid, an upward force acts on it which is called upthrust or buoyant force.

Archimedes principle: When a body is immersed fully or partially in a fluid, it experiences an upward force that is equal to the weight of the fluid displaced by it.

On this page, you will find Force and Laws of Motion Class 9 Notes Science Chapter 9 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 9 Force and Laws of Motion will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 9 Notes Force and Laws of Motion

Force and Laws of Motion Class 9 Notes Understanding the Lesson

1. Force
It is entity which when applied on a body changes or tends to change a body’s

• state of rest
• state of uniform motion
• direction of motion
•  shape

2. Balanced forces
When a number of forces acting simultaneously on a body do not bring about any change in state of rest or of uniform motion along a straight line, then forces acting on a body are said to be balanced forces.

3. Unbalanced forces
When a number of forces acting simultaneously on a body bring about a change in its state of rest or of uniform motion along a straight line, then these forces acting on the body are said to be unbalanced forces.

4. Newton’s first law of motion
An object remains in a state of rest or of uniform motion in a straight line unless compelled to change that state by an applied force.

5. Inertia
Inertia is the natural tendency of an object to resist a change in its state of motion or of rest.

6. The mass of an object is a measure of its inertia.
Examples:

• Passenger tends to fall backward, when a bus starts suddenly.
• Falling of fruits and leaves by a shaking tree.
• When a carpet is beaten with a stick, dust particles come out.
• When the card covering a glass tumbler is flicked with the finger coin placed over it falls in the tumbler.

7. Momentum (P)

• Momentum gives an idea about the quantity of motion contained in a body.
• The momentum (P) of an object is defined as the product of its mass (m) and velocity (v).
  P = mv
• Momentum is vector quantity and its unit is kg ms^-1.

8. Second law of motion
The second law of motion states that the rate of change of momentum of an object is proportional to the applied unbalanced force in the direction of force.

9. Mathematical formulation of second law of motion
Suppose an object of mass, m is moving along a straight line with an initial velocity, v. It is uniformly accel-erated to velocity, v in time, t by application of constant force F throughout the time, t. The initial and final momentum of the object will be, P₁ = mu and P₂ = mv
respectively.


∴ F =ma
K is proportionality constant and the value So,
SI unit of force is newton.

10. First law of motion can be stated from the second law
F = ma
\(F=\frac{m(v-u)}{t}\)
Ft = mv – mu
when F = 0, v – u. This means that the object will continue moving with uniform velocity, u throughout the time, t. If u is zero then v will also be zero. That is, the object will remain at rest.

11. Example of second law of motion:
As we know that \(\text { F } \alpha \frac{1}{t}\)

• A cricket players lowers his hand while catching the ball to increase the time so that impact of force decreases.
• A karate player can break a pile of tiles with a single blow of his hand. This is because, as time decreases impact of force increases.
• Vehicles are fitted with shockers. The shockers increase the time of transmission of the force of the jerk to reach the floor of the vehicle. Hence less jerk is experienced by the passengers.

12. Third law of motion
According to the third law of motion, every action there is an equal and opposite reaction and they act on two different bodies.

Example of third law of motion:

• Recoiling of gun.
• When a man jumps out from a boat, the boat moves backward.

13. Conservation of momentum
In an isolated system (where there is no external force), the total momentum remains conserved.
m_Au_A + m_Bu_B = m_Av_A + m_Bv_B

14. Derivation
Suppose two objects of mass m_A and m_B are travelling in the same direction along a straight line at different velocity u_A and u_B respectively, and there are no external unbalanced forces acting on them. Let u_A > u_B and two balls collide each other. During collision which last for a time t, ball A exerts force on ball B and ball B exerts force F_BA on ball A. Suppose v_A and i>_B are the velocities after collision.

15. Illustration of conservation of momentum

• Recoil of gun.
• Rocket propulsion.
• Inflated balloon lying on the surface of a floor moves forward when pierced with a pin.

Class 9 Science Chapter 9 Notes Important Terms

Force: It is entity which when applied on a body changes or tends to change a body’s.

• state of rest
• state of uniform motion
• direction of motion
• shape

Balanced forces: When a number of forces acting simultaneously on a body do not bring about any change in state of rest or of uniform motion along a straight line, then forces acting on a body are said to be balanced forces.

Unbalanced forces: When a number of forces acting simultaneously on a body bring about change in its state of rest or of uniform motion along a straight line, then these forces acting on the body are said to be unbalanced forces.

Inertia: Inertia is the natural tendency of an object to resist a change in its state of motion or of rest.

Momentum: Momentum of a body is product of its mass and velocity.

Conservation of momentum: In an isolated system the total momentum remains conserved.

On this page, you will find Motion Class 9 Notes Science Chapter 8 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 8 Motion will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 8 Notes Motion

Motion Class 9 Notes Understanding the Lesson

1. Rest: A body is said to be at rest if its position does not change with respect to a fixed point taken as a reference point in its surrounding with the passage of time.

2. Motion: A body is said to be in motion if its position is changes with respect to a fixed point taken as a reference point in its surrounding with the passage of time.

3. Scalar quantity: A physical quantity which is described completely by its magnitude only, is called a scalar quantity.

4. Vector quantity: A physical quantity that has magnitude as well as direction is called a vector quantity. Distance: The total path length travelled by a body in a given interval of time is called distance. Displacement: The shortest distance measured from initial to the final position of an object is known as displacement.

5. Difference between distance and displacement

Distance	Displacement
1.   It is the actual length of the path covered by a moving body. 2.   It is always positive or zero. 3.   It is a scalar quantity.	1.    It is the shortest distance measured between the initial and final position. 2.    It may be positive, negative or zero. 3.    It is a vector quantity.

SI unit of distance and displacement is metre (m).

6. Uniform motion: A body moving in straight line has a uniform motion if it travels equal distance in equal intervals of time.

7. Non-uniform motion: A body has a non-uniform motion if it travels unequal distances in equal intervals of time.

8. Speed: The speed of a body is defined as distance travelled by it per unit time.

Speed is scalar quantity and SI unit of speed is m/s.

9. Average speed: It is defined as the total distance travelled by a body divided by the total time taken to cover this distance.

SI unit of speed and velocity is same.

Difference between speed and velocity

Speed	Velocity
1.   Speed is the ratio of distance and time. 2.   Speed is always positive. 3.   Speed is a scalar quantity.	1.  Velocity is ratio of displacement and time. 2.  Velocity may be negative or positive. 3.  Velocity is a vector quantity.

10. Acceleration: The rate of change of velocity of a body with respect to time is called its acceleration.

\(\text { Acceleration }=\frac{\text { Change in velocity }}{\text { time taken }}\)
\(a=\frac{v-u}{t}\)

Here, u – initial velocity
v = final velocity
t = time

11. Acceleration is a vector quantity and its SI unit is m/s².

12. If a body is travelling with uniform acceleration then its average velocity can be expressed as

\(v_{\text {avg }}=\frac{u+v}{2}\)
Here, u = initial velocity
v – final velocity

13. If the speed of a body is continuously increasing, the body is said to be continuously accelerating. If the speed of body is continuously decreasing, the body is said to be retarding.

14. Graphical Representation of Motion
Distance-time graph (Position time graph)

15. Slope of velocity-time graph gives speed and velocity

16. velocity-time graph

17. Slope of velocity-time graph gives distance and displacement.

18. Equation of motion by graphical method
Let us consider a body moving with acceleration a where u is initial velocity and v is final velocity, s is displacement of the object and t is time interval.

(i) v = u + at
We know that slope of v – t graph gives acceleration so slope
\(=a=\frac{v-u}{t-o}\)
\(\begin{array}{l}
a=\frac{v-u}{t} \\
v=u+\text { at }
\end{array}\)

(ii) \(s=u t+\frac{1}{2} a t^{2}\)
We know that area under v -1 graph gives displacement.
Area = s = area of triangle CDE + area of rectangle ABCE
\(s=u t+\frac{1}{2} \times t \times(v-u)\)
Putting the value of v – u.
\(s=u t+\frac{1}{2} \mathrm{at}^{2}\)

(iii) v² – u² = 2as
a where u is initial velocity and v is final velocity, s is displacement of the object and t is time interval.
\(s=\frac{1}{2} \times(v+u) \times t\)
\(\text { from } 1\left(t=\frac{v-u}{a}\right)\)
Putting the value of t.
v² – u² = 2as

19. Uniform circular motion
When an object moves in a circular path with uniform speed, its motion is called uniform circular motion.
\(v=\frac{2 \pi r}{t}\)

If a body is moving in a circular path and completes one round (2πr distance) in time, speed is given by
Uniform circular motion is accelerated motion.

Class 9 Science Chapter 8 Notes Important Terms

State of rest: A body is said to be at rest if it does not change its position with respect to a fixed point taken as a reference point in its surroundings with passage of time.

State of motion: A body is said to be in motion if it changes its position with respect to a fixed point as a reference point in its surroundings with the passage of time.

Scalar quantity: A physical quantity which is described completely by its magnitude only, is called scalar quantity.

Vector quantity: A physical quantity which has magnitude as well as direction and obeys the vector addition is called vector quantity.

Distance: The total path length travelled by a body in a given interval of time is called distance.

Displacement: The shortest distance measured from initial to the final position of an object is known as displacement.

Uniform motion: A body moving in a straight line has a uniform motion, if it travels equal distance in equal intervals of time.

Non-uniform motion: A body has a non-uniform motion, if it travels unequal distances in equal intervals of time.

Speed: The speed of a body is defined as distance travelled by it per unit time.

Velocity: Velocity is defined as displacement per unit time.

Acceleration: The rate of change of velocity of a body with respect to time is called its acceleration.

Retardation: When acceleration of a body is opposite to its velocity, it is called retardation.

Uniform circular motion: When an object is moving in a circular path with a constant speed, the motion of the object is said to be uniform circular motion.

On this page, you will find Diversity in Living Organisms Class 9 Notes Science Chapter 7 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 7 Diversity in Living Organisms will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 7 Notes Diversity in Living Organisms

Diversity in Living Organisms Class 9 Notes Understanding the Lesson

1. What is classification?
Grouping the organisms on the basis of their similarities and differences is called classification.

2. Need for classification

• To provide information regarding diversity of plants and animals on the Earth.
• Understand the interrelationship between different groups of plants and animals.
• To find similarities or dissimilarities in their characteristic features.
• To identify the organism.
• To indicate evolutionary trends.

3. Characteristics or criteria of classification

• Complexity of structure: Prokaryotes or Eukaryotes
• Body organisation: Unicellular or Multicellular
• Mode of obtaining Nutrition: Autotrophic or Heterotrophic
• Evolutionary relationship
• Presence or absence of cell wall

4. Kingdom
It is the highest category of classification. Each kingdom has some similar fundamental characteristics in all organisms grouped under that kingdom. The five-kingdom classification was given by R.H. Whittaker.

Characteristics	Monera	Protista	Fungi	Plantae	Animalia
Complexity of structure	Prokaryotes	Eukaryotes	Eukaryotes	Eukaryotes	Eukaryotes
Body organisation	Unicellular	Unicellular	Multicellular (at some stage of life)	Multicellular	Multicellular
Mode of nutrition	Autotrophic or Heterotrophic	Autotrophic or Heterotrophic	Heterotrophic Parasitic Saprophytic Symbiotic	Autotrophic	Heterotrophic

 

Characteristics	Monera	Protista	Fungi	Plantae	Animalia
Cell wall	Present or absent	Present or absent	Present (made up of chitin)	Present (made up of cellulose)	Absent
Appendages	Cilia or flagella for movement	Cilia, flagella or pseudopodia for movement	Do not move	Do not move	Different appendages
	e.g., Bacteria	e.g., Amoeba	e.g., Mushroom	e.g., Rose	e.g., Monkey

Differentiate between:

S. No.	Thallophyta	Bryophyta	Pteridophyta
1.	Plant body thallus like, not differentiated into root, stem or leaf.	Plant body does not have true root, stem or leaf but shows root­like and leaf-like structures.	Plants have true root stem or leaf.
2.	Vascular system absent.	True vascular system is absent.	True vascular system is present.
3.	Predominantly aquatic.	They live on land and in water. They are known as the Amphibians of the plant kingdom.	They are terrestrial, i.e., they live on land.
4.	No embryo formation after fertilization. e.g., Algae	Embryo formed after fertilisation. e.g., Mosses, liverworts .	Embryo formed after fertilisation. e.g., Ferns

 

S. No.	Cryptogamae	Phanerogamae
1.	Reproductive organs are hidden.	Reproductive organs are visible.
2.	Fertilisation results in the formation of a naked embryo called spores.	Fertilisation results in the formation of seeds which consists of embryo and cotyledons.
3.	Water is required for fertilisation.	Water is not required for fertilisation always except for aquatic phanerogams.
	e.g., Thallophyta, Bryophyta, Pteridophyta	e.g., Gymnospermae and Angiospermae

 

S. No.	Gymnospermae	Angiospermae
1.	Plants bear naked seeds.	Seeds are present inside fruits.
2.	Xylem is without vessels and phloem is without companion cells.	Well developed vascular tissue present.
3.	Plants are perennial, woody and evergreen.	Plants are annual, biennial, perennial, woody or green.
	e.g., Pinus, Cycas	e.g., Neem, Rose, Mango

 

S. No.	Monocotyledonous Plants	Dicotyledonous Plants
1.	Single cotyledon in seeds.	Two cotyledons in seeds.
2.	Fibrous roots.	Tap roots.
3.	Parallel venation.	Reticulate venation.
	e.g., Lily, Rice, Wheat	e.g., Hibiscus, Pea, Gram

5. Characteristic features of different Phyla of Kingdom Animalia Porifera

• Porifera means organisms with holes.
• Non-motile animals attached to solid support
• Holes or pores all over body
• Have canal system that helps in circulating water throughout the body to bring in food and oxygen.
• Body covered with hard outside layer or skeleton
• Minimal differentiation of body and division into tissues
• Commonly called sponges found in marine habitats
• Acoelomate (without body cavity)
  Examples: Euplectella, Sycon, Spongilla

6. Coelenterata

• Animals living in water
• More body design differentiation
• Diploblastic body
• Some species live in colonies (corals) while others have a solitary life span (Hydra)
  Examples: Jelly fish, Sea Anemone, Hydra

7. Platyhelminthes

• Body is complexly designed
• Bilaterally symmetrical body
• Triploblastic body
• Acoelomate
• Body flattened dorsi-ventrally, so called flatworms
• Free living or parasitic
  Examples: Planarian (free living) liver flukes, tapeworms (Parasitic)

8. Nematodes

• Bilaterally symmetrical
• Triploblastic body
• Cylindrical body
• Tissues present but no real organs
• Presence of pseudo coelom, a sort of body cavity
• Familiar as parasitic worms causing diseases, present in intestines
  Examples: Ascaris, Wucheraria

9. Annelida

• Bilaterally symmetrical
• Triploblastic
• Coelomate (having a body cavity or coelon)
• Extensive organ differentiation
• Segmented body (Metamerism)
• Found in fresh water, marine and on land
  Examples: Earthworms, Leech, Nereis

10. Arthropoda

• Largest group of animals
• Bilaterally symmetrical
• Segmented body
• Open circulatory system
• Coelomate
• Arthropoda means jointed legs
  Examples: Prawns, Butterflies, Housefly, Cockroach

11. Mollusca

• Bilaterally symmetrical
• Coelomic cavity is reduced
• Little segmentation
• Open circulatory system
• Kidney like organ for excretion
• There is a foot like structure for moving around
  Examples: Snails, mussels, Chiton, Octopus, Unio, Pila

12. Echinodermata

• They are spiny skinned organisms
• Echinos’ means hedgehog and ‘Derma’ means skin.
• Exclusively free living marine animals
• Triploblastic
• Acoelomate
• Peculiar water driven tube system
• Hard calcium carbonate structures as skeleton
  Examples: Star fish, sea urchin, feather star, sea cucumber

13. Protochordate

• Bilaterally symmetrical
• Triploblastic
• Coelomate
• Notochord present during larval stage
• Provides place for muscles to attach for easy movement
• Marine animals
  Examples: Balanoglossus, Herdmania, Amphioxu

14. Vertebrata

• Have a true vertebral column and internal skeleton
• Bilaterally symmetrical
• Triploblastic
• Coelomate and segmented
• Complex differentiation of body tissues and organs

15. All chordates possess the following features:

• Have a notochord
• Have a dorsal nerve cord
• Are triploblastic
• Have paired gill pouches in some stage of their life cycle
• Are coelomate

16. Vertebrates are grouped into 5 classes
Pisces

• Exclusively aquatic animals
• Skin covered with scales or plates
• Obtain oxygen dissolved in water
• Streamlined body and muscular tail for movement in water
• Cold-blooded
• Two-chambered heart
• Lays eggs in water

17. Are of two types:

• Cartilaginous fish (skeleton made entirely of cartilage), e.g., Shark
• Bony fish (skeleton made of both cartilages and bones), e.g., Rohu, Tima

18. Amphibia

• Lack scales
• Have mucus glands in skin
• Cold-blooded
• Three-chambered heart
• Respiration through gills, lungs or skin
• Lay eggs in water
• Live both on land and in water
  Examples: Frogs, toads, salamander, etc.

19. Reptilia

• Have scales
• Three-chambered heart but crocodiles have four chambered heart
• Cold-blooded
• Breathe through lungs
• Lay eggs with tough coverings so they do not lay eggs in water
  Examples: Snakes, turtles, lizards, crocodiles, chameleon

20. Aves

• Outside covering of feathers
• Four-chambered heart
• Warm-blooded
• Breathe through lungs
• Lay eggs
• Two forelimbs modified into wings for flight
  Examples: All birds like crow, pigeon, peacock, etc.

21. Mammalia

• Skin has hairs, oil and sweat glands
• Four-chambered heart
• Warm-blooded.
• Most of them give birth to young ones
• Few like Platypus and Echidna lay eggs
• Some like kangaroos give birth to poorly developed young ones
• Mammary glands present for production of milk to nourish their young ones
  Examples: Cat, human, rat, bat, whale, etc.

21. Nomenclature: System of assigning names or terms to the organisms is called as nomenclature. The names given to the organism can be

• Common name or
• Scientific name.

Common names cannot be used in the same way by the scientist world over and can often result in confusion. To avoid this, a system of scientific names has been proposed.

Binomial System of Nomenclature: The binomial system of nomenclature assigns two names to the organism in order to identify it first is the generic name (genus) and the second is the specific epithet (species). This system of nomenclature was given by Carolus Linnaeus.

22. Convention for writing the scientific names:

• The name of the genus begins with a capital letter.
• The name of the species begins with a small letter.
• When printed, the scientific name is given in italics.
• When written by hand, the genus name and the species name have to be underlined separately.

23. Scientific names of some organisms:

• Tiger – Panthera tigris
• Peacock – Pauo cristatus
• Mango – Mangifera indica
• Lotus – Nelumbo nucifera
• Neem – Azadiraehta indica
• Potato – Solanum tuberosum
• Ant – Hymenopetrous formicidae
• Frog – Rana tigrina
• Rose – Rosa indica
• Pea – Pisum sativum

Class 9 Science Chapter 7 Notes Important Terms

Prokaryotes: Organisms which do not have a clearly demarcated nucleus and other organelles.

Eukaryotes: Organisms having membrane bound cell organelles and a well-defined nucleus.

Unicellular: Organisms having only one cell in their body.

Multicellular: Organisms having many cells in their body.

Autotrophs: Organisms synthesising their own food by photosynthesis.

Heterotrophs: Organisms which depend on other organisms for their food.

Bilateral symmetry: The body organisation in which the left and right halves have same body design.

Radial symmetry: Arrangement of similar parts around a central body axis as in a wheel.

Diploblastic: Animals having a body made up of two layers of cells i.e., ectoderm and endoderm.

On this page, you will find Tissues Class 9 Notes Science Chapter 6 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 6 Tissues will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 6 Notes Tissues

Tissues Class 9 Notes Understanding the Lesson

1. A single cell performs all the basic functions like digestion, respiration, excretion, etc. in order to sustain life in the unicellular organisms like Amoeba. In multicellular organisms like human beings, each specialised function to sustain life is taken up by a different group of cells.

2. Division of labour: The multicellular organisms show division of labour as each function is carried out by a cluster of specialised cells at a definite place in the body.
For example:
In human beings, muscle cells contract and relax to cause movement, nerve cells carry messages, blood flows to transport oxygen, etc. In plants, vascular tissues called xylem and phloem conduct water and food respectively from one part of the plant to the other parts.

3. Tissue: A group of cells that are similar in structure and/or work together to achieve a particular function forms a tissue. Example: Blood, phloem and muscle. Plant tissues are classified as growing or meristematic tissue and permanent tissue.

4. Meristematic tissue: This tissue consists of cells which continuously divide to produce new cells. The cells of this tissue are very active, lack vacuoles, have dense cytoplasm, thin cellulosic cell walls and prominent nuclei.

5. Location of meristematic tissue: This tissue is present only at specific regions of the plant like the root tip, shoot tip and at the base of intemodes and leaves.

6. Types of meristematic tissue: They are classified as apical, lateral and intercalary meristematic tissue based on the region where they are present.

• Apical meristem: It is present at the growing tips of stems and roots and results in increase in the length of the stem and the root.
• Lateral meristem (cambium): It helps to increase the girth of the stem or root.
• Intercalary meristem: It is present at the base of the leaves or intemodes.

5. Permanent tissue: Consists of cells which have taken up a specific role and lost the ability to divide.
It is of two types:

• Simple tissue: It is made up of only one type of cells. Its three types are: parenchyma, collenchyma and sclerenchyma.
• Complex tissue: It is made up of more than one type of cells. They are the conducting tissues called xylem and phloem.

6. Differentiation: The process of taking up a permanent shape, size, and a function by the cells is called differentiation.

7. Types of simple tissue:
(a) Parenchyma: They are loosely packed living cells, with thin cell walls and large intercellular spaces. They provide support to plants and store food. It is called chlorenchyma if it contains chlorophyll and performs photosynthesis. The parenchyma of aquatic plants have large cavities to provide buoyancy to the plants to help them float. Such type of parenchyma is called aerenchyma.

(b) Collenchyma: It consists of living, elongated cells that are irregularly thickened at the corners and have a very little intercellular space. It allows easy bending in various parts of a plant (leaf, stem) without breaking. It also provides mechanical support to plants like in the leaf stalks below the epidermis.

(c) Sclerenchyma: This tissue consists of dead cells which makes the plant hard and stiff. The cells are long and narrow as the walls are thickened (often so thick that there is no internal space inside the cell) due to lignin (a chemical substance which acts as cement and hardens them). This tissue provides strength to the plants and is present in stems, around vascular bundles, in the veins of leaves and in the hard covering of seeds and nuts.

8. Epidermis: The outermost layer of cells covering an organism is called epidermis. It is usually made up of a single layer of cells and gives protection. The epidermis may be thicker in some plants living in dry habitats or often secrete a waxy, water-resistant layer on their outer surface called cutin (chemical substance with waterproof quality) to prevent water loss.

The epidermis of leaves have small pores called stomata which are enclosed by two kidney shaped cells called guard cells. Stomata help in gaseous exchange and transpiration. The epidermal cells of roots bear root hairs that greatly increase the total absorptive surface area of the roots for absorption of water.

9. Cork: A strip of secondary meristem replaces the epidermis of the older stem and cuts off cells towards outside to form a several-layer thick cork or the bark of the tree. Cells of cork are dead, compactly arranged without intercellular spaces and have a chemical called suberin in their walls that makes them impervious to gases and water.

10. Complex Permanent Tissue: These tissues are made of more than one type of cells which coordinate to perform a common function, e.g., Xylem and phloem. They are mainly conducting tissues and constitute a vascular bundle.

(a) Xylem: Xylem consists of tracheids, vessels, xylem parenchyma and xylem fibres. All the cells of xylem except the xylem parenchyma are dead. Xylem helps to transport water and minerals. Tracheids and vessels help in vertical transport whereas the parenchyma stores food and helps in the sideways conduction of water. Fibres are mainly supportive in function.

(b) Phloem: Phloem has four elements called sieve tubes, companion cells, phloem fibres and the phloem parenchyma. All cells of phloem are living except the phloem fibres. Phloem transports food from leaves to other parts of the plant.

11. Animal Tissues: The animal tissues are of four types: epithelial tissue, connective tissue, muscular tissue and nervous tissue.

12. Epithelial Tissue: They are the covering or protective tissues and cover most organs and cavities in the animal body. These cells are tightly packed, form a continuous sheet and are almost without any intercellular spaces between them. e.g., skin, the lining of the mouth, the lining of blood vessels, lung alveoli and kidney tubules are all made of epithelial tissue. All epithelium is usually separated from the underlying tissue by an extracellular fibrous basement membrane. The types of epithelium on the basis of their structure and functions are:

(a) Squamous epithelium: Consists of flattened cells. Present in oesophagus and lining of the mouth. Skin epithelial cells are arranged in many layers to prevent wear and tear and are called as stratified squamous epithelium.

(b) Columnar epithelium: Has tall or ‘pillar-like’ cells. It forms inner lining of the intestine.

(c) Cuboidal epithelium: Has cube-shaped cells. It forms the lining of kidney tubules and ducts of salivary glands, where it provides mechanical support.

(d) Ciliated epithelium: Have cilia on the outer surfaces of epithelial cells. The cilia can move and their movement pushes the mucus in the respiratory tract forward to clear it.

(e) Glandular epithelium: Has gland cells which secrete substances at the epithelial surface.

13. Connective Tissue: The cells of connective tissue are loosely spaced and embedded in an intercellular matrix which may be jelly like, fluid, dense or rigid, e.g., blood, bone, cartilage, etc.

(a) Blood: It has a fluid (liquid) matrix called plasma having red blood cells (RBCs), white blood cells (WBCs) and platelets. Blood helps in the transport of gases, digested food, hormones and waste materials to different parts of the body.

(b) Bone: It has bone cells embedded in a hard matrix composed of calcium and phosphorus compounds. It is a strong and non-flexible tissue which forms a framework that supports the body, anchors the muscles and supports the main organs of the body.

(c) Cartilage: It has widely spaced cells and a solid matrix composed of proteins and sugars. It helps to smoothen bone surfaces at joints and is also present in the nose, ear, trachea and larynx.

(d) Areolar connective tissue: It fills the space inside the organs, supports internal organs and helps in repair of tissues. It is found between the skin and muscles, around blood vessels and nerves and in the bone marrow.

(e) Adipose tissue: It is a fat storing tissue having cells filled with fat globules. It is found below the skin and between the internal organs.

(f) Ligament: It is the connective tissue which connects two bones. This tissue has very little matrix, is very elastic and has considerable strength.

(g) Tendon: It is the connective tissue which connects muscles to bones. It is a fibrous tissue with great strength but limited flexibility.

14. Muscular Tissue: This tissue is responsible for movement in our body and consists of elongated cells, also called muscle fibres. Muscles contain special proteins called contractile proteins, which contract and relax to cause movement.

(а) Striated Muscles: These muscles are also called skeletal muscles as they are mostly attached to bones and help in body movement. These muscles show alternate light and dark bands. These are long, cylindrical, unbranched and multinucleate. These are voluntary muscles as we can move them by conscious will, e.g., muscles of our limbs.

(b) Unstriated Muscles: They are also called smooth muscles or unstriated muscles as they do not have light and dark bands. The cells are long, uninucleate, involuntary in nature and spindle shaped. They are present in iris of the eye, ureters, blood vessels, alimentary canal and bronchi of lungs.

(c) Cardiac Muscles: These are the muscles of the heart which show rhythmic contraction and relaxation throughout life. They are involuntary, cylindrical, branched and uninucleate.

15. Nervous Tissue: The cells of this tissue are called nerve cells or neurons. Each neuron consists of a cell body with a nucleus and cytoplasm, a single long part called the axon, and many short branched parts called dendrites. The cells of the nervous tissue are highly specialised for transmitting the stimulus from one place to another within the body on being stimulated. The brain, spinal cord and nerves are composed of the nervous tissue. A nerve consists of many nerve fibres bound together by connective tissue.

Class 9 Science Chapter 6 Notes Important Terms

Tissue: A group of cells that are similar in structure and/or work together to achieve a particular function.

Meristematic tissue: This tissue that consists of cells which continuously divide to produce new cells.

Permanent tissue: The tissue which consists of cells which have taken up a specific role and lost the ability to divide.

Differentiation: The process of taking up a permanent shape, size, and a function by the cells is called differentiation.

Chlorenchyma: Parenchyma which contains chlorophyll and performs photosynthesis.

Aerenchyma: Parenchyma which contains large cavities to provide buoyancy to the aquatic plants to help them float.

Cambium: It is a lateral meristem which helps in increasing the girth of the stem or root.

Lignin: A chemical substance which acts as cement and hardens the cells of sclerenchyma.

Cutin: A chemical substance with waterproof quality present in epidermis of leaves to prevent water loss by transpiration.

Suberin: A chemical present in the walls of cork cells that makes them impervious to gases and water.

Adipose tissue: It is a fat storing tissue having cells filled with fat globules.

Ligament: It is the connective tissue which connects two bones. This tissue has very little matrix, is very elastic and has considerable strength.

Tendon: It is the connective tissue which connects muscles to bones. It is a fibrous tissue with great strength but limited flexibility.

Contractile proteins: Special proteins present in muscles which contract and relax to cause movement of body parts.

Nerve: A nerve consists of many nerve fibres bound together by connective tissue.

On this page, you will find The Fundamental Unit of Life Class 9 Notes Science Chapter 5 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 5 The Fundamental Unit of Life will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 5 The Fundamental Unit of Life

The Fundamental Unit of Life Class 9 Notes Understanding the Lesson

1. Robert Hooke: In 1665, he discovered cell in a thin slice of cork (bark of cork tree) by using a self designed microscope. The structure consisted of many little compartments which resembled the structure of a honeycomb. He called boxes as ‘cell’ which is Latin word for ‘a little room’.

2. Leeuwenhoek: In 1674, discovered the free-living cells in pond water for the first time by using an improved microscope.

3. Robert Brown: In 1831, discovered the nucleus in the cell.

4. Piirkinje: In 1839, coined the term ‘protoplasm’ for the fluid substance of the cell.

5. Schleiden (1838) and Schwann (1839): Put forth the cell theory, which said that:

• all the plants and animals are composed of cells and
• cell is the basic unit of life.

6. Virchow: In 1855, expanded the cell theory by suggesting ‘Omni cellula-e-cellula’ which means all cells arise from pre-existing cells.

7. Unicellular organisms: Organisms which have only a single cell, e.gAmoeba, Paramecium, Chlamydomonas, bacteria, etc.

8. Multicellular organisms: Organisms which consist of more than one cell e.g., Plants, animals, fungi, etc.

9. Cell division: It is the process by which a cell divides to form new cells. This supports the fact that, all cells arise from the existing cells.

10. The shape and size of cells are related to the specific function they perform: Amoeba can change its shape as per the conditions or its need whereas for most of the other cases, the cell shape is more or less fixed, e.g., nerve cells have a typical shape.

11. Division of Labour: In all multicellular organisms there is a division of labour. This means that different parts of the body perform different functions. For example, the stomach helps in digestion; blood is pumped by the heart, etc. Division of labour can also be seen within a single cell.

12. Three main parts of a cell: Most cells (excluding bacteria) have three main parts:

• Plasma membrane/Cell Membrane
• Nucleus
• Cytoplasm

13. Plasma Membrane or Cell Membrane

• It is the outermost covering of the cell.
• It separates the contents of the cell from its external environment.
• It is mainly composed of lipids and proteins.
• It is called selectively permeable as it permits the entry and exit of only some materials in and out of the cell.

14. Diffusion: The movement of a substance from a region of its high concentration to the region of its low concentration is called diffusion. Diffusion helps in gaseous exchange between the cells as well as the cell and its external environment.

15. Osmosis: The spontaneous movement of water molecules from a region of its high concentration to the region of its low concentration through a selectively permeable membrane is called osmosis.

Effect on animal cell or a plant cell put into a solution of sugar or salt in water

Kind of solution	Nature of surrounding medium	Effect on cell	Result
Hypotonic solution	Medium surrounding the cell has a higher water concentration than the cell (outside solution is very dilute).	Water will enter the cell by osmosis.	Cell is likely to swell up.
Isotonic solution	Medium surrounding the cell has exactly the same water concentration as the cell.	There is no overall movement of water.	Cell will stay the same size.
Hypertonic solution	Medium surrounding the cell has a lower concentration of water than the cell (very concentrated solution).	Cell will lose water by osmosis.	Cell will shrink.

16. Cell Wall

• It is a rigid outer covering which lies outside the plasma membrane.
• It is made of cellulose which provides structural strength to plants.
• The shrinkage or contraction of the contents of the cell away from the cell wall when a living plant cell loses water through osmosis is known as plasmolysis.

17. Nucleus

• It is a dark coloured, spherical or oval, dot-like structure near the centre of each cell.
• It is the control centre of the cell as it controls all the activities of the cell.
• It has a double-layered covering called nuclear membrane.
• The nuclear membrane has pores which allow the transfer of materials from inside the nucleus to its outside, that is, to the cytoplasm.
• The nucleus plays a central role in cellular reproduction (process by which a single cell divides and forms two new cells).
•  Nucleus along with the environment directs the chemical activities of the cell to determine the way the cell will develop and the form it will exhibit at maturity.
• Nuclear region of the cell may be poorly defined due to the absence of a nuclear membrane in some organisms like bacteria. Such an undefined nuclear region containing only nucleic acids is called a nucleoid.

18. Chromosomes

• The nucleus contains chromosomes, which are visible as rod-shaped structures only when the cell is about to divide.
• Chromosomes contain information for inheritance of features from parents to next generation in the form of DNA (Deoxyribo Nucleic Acid) molecules.
• Chromosomes are composed of DNA and protein.

19. Genes
Functional segments of DNA are called genes.
Chromatin Material:

• DNA is present as part of chromatin material in the cells which are not dividing.
• Chromatin material is visible as entangled mass of thread-like structures.
• Chromatin material gets organised into chromosomes, when the cell is about to divide.

20. Types of organisms on the basis of the nature of nucleus and nuclear membrane

Prokaryotes	Eukaryotes
(i) Organisms whose cells lack a well defined nuclear membrane.	(i) Organisms with cells having a well defined nuclear membrane.
(ii) They lack membrane bound cell organelles.	(ii) They have membrane bound cell organelles.
(iii) Size is generally small (1-10 pm).	(iii) Size is generally large (5-100 pm).
(iv) Have a single chromosome.	(iv) Have more than one chromosome.

20. Cytoplasm

• It is the fluid content enclosed by the plasma membrane.
• It contains many specialised cell organelles.

21. Cell Organelles
Cell organelles are parts of the cell which are specialised for carrying out one or more vital functions, analogous to the organs of the human body.

22. A. Endoplasmic Reticulum (ER)
(i) Consists of a large network of membrane-bound tubes and sheets which appear as long tubules or round or oblong bags (vesicles).

(ii) ER serves as channels for the transport of materials (especially proteins) between various regions of the cytoplasm or between the cytoplasm and the nucleus.

(iii) It also functions as a cytoplasmic framework providing a surface for some of the biochemical activities of the cell.

(iv) ER are of two types:
Rough endoplasmic reticulum (RER) and
Smooth endoplasmic reticulum (SER).

(v) Rough endoplasmic reticulum

• It looks rough as it has particles called ribosomes attached to its surface. Ribosomes are the site of protein synthesis.

(vi) Smooth endoplasmic reticulum

• It helps in the manufacture of fat molecules, or lipids, important for cell function.
• Some proteins and lipids made by SER help in building the cell membrane and this process is known
  as membrane biogenesis.
• Helps in detoxifying many poisons and drugs in the liver cells of the group of vertebrates.

B. Golgi Apparatus

• First described by Camillo Golgi.
• It has membrane-bound vesicles arranged approximately parallel to each other in stacks called cisterns.
• They constitute another portion of a complex cellular membrane system as their membranes often have connections with the membranes of ER.
•  Its functions include storage, modification and packaging of products in vesicles.
• Golgi apparatus packages and dispatches the material synthesised near the ER to various targets inside and outside the cell.
• They are also involved in the formation oflysosomes.

C. Lysosomes

• They are membrane-bound sacs filled with digestive enzymes made by RER.
• They are waste disposal system of the cell as they help to keep the cell clean by digesting any foreign material as well as worn-out cell organelles.
• Lysosomes have powerful digestive enzymes capable of breaking down all organic materials.
• Lysosomes are also known as the ‘suicide bags’ of a cell because if the cell gets damaged during disturbance in cellular metabolism, the lysosomes may burst and its enzymes digest their own cell.

D. Mitochondria

• Also known as the powerhouses of the cell as the energy required for various chemical activities needed for life is released by mitochondria in the form of Adenosine triphosphate – ATP (ATP is known as the energy currency of the cell).
• Mitochondrion is a double-membrane structure whose outer membrane is very porous while the inner
  membrane is deeply folded to form cristae. Cristae are folds which create a large surface area for ATP’ generating chemical reactions.
• Mitochondria have their own DNA and ribosomes so they can make some of their own proteins.

E. Plastids

• Plastids are present only in plant cells and are of two types – chromoplasts (coloured plastids) and leucoplasts (white or colourless plastids).
• Chlorophyll containing plastids are known as chloroplasts and help in photosynthesis.
• Leucoplasts store starch (amyloplast), oils (elaioplasts) and protein granules (aleuroplasts).
• The plastids internally consist of numerous membrane layers embedded in a material called the stroma.
• Plastids have their own DNA and ribosomes so they can make some of their own proteins.

F. Vacuoles

• Vacuoles are storage sacs for solid or liquid contents like amino acids, sugars, various organic acids and some proteins.
• Small-sized vacuoles are present in animal cells while plant cells have very large vacuoles. A large central vacuole may occupy 50-90% of the cell volume in some plant cells.
• The vacuoles are full of cell sap and provide turgidity and rigidity to the cell in plant cells.
• Food vacuole found in Amoeba contains the food items that the Amoeba has consumed.
• Contractile vacuole found in some unicellular organisms help in expelling excess water and some wastes f from the cell.

Class 9 Science Chapter 5 Notes Important Terms

Unicellular organisms: They are single-celled organisms, e.g., Amoeba, Paramecium, Chlamydomonas, bacteria, etc.

Multicellular organisms: They are composed of more than one cell, e.g., plants, animals, fungi, etc. Diffusion: The movement of a substance from a region of its high concentration to the region of its low concentration is called diffusion.

Osmosis: The spontaneous movement of water molecules from a region of its high concentration to the region of its low concentration through a selectively permeable membrane is called osmosis.

Hypotonic solution: If the medium surrounding the cell has a higher water concentration than the cell i.e., outside solution is very dilute, then it is called a hypotonic solution.

Isotonic solution: If the medium surrounding the cell has exactly the same water concentration as the cell, then it is called isotonic solution.

Hypertonic solution: If the medium surrounding the cell has a lower concentration of water than the cell i.e., very concentrated solution, then it is called hypertonic solution.

Plasmolysis: The shrinkage or contraction of the contents of the cell away from the cell wall when a living plant cell loses water through osmosis is known as plasmolysis.

Genes: Functional segments of deoxyribonucleic acid (DNA) are called genes.

Prokaryotes: The single celled organisms which lack a well-defined nuclear membrane are called prokaryotes.

Eukaryotes: The single celled or multicellular organisms which have a well defined nuclear membrane are called eukaryotes.

Membrane biogenesis: Some proteins and lipids made by SER help in building the cell membrane and this process is known as membrane biogenesis.

Amyloplast: The starch containing leucoplasts are called amyloplast.

Elaioplast: The oil containing leucoplasts are called elaioplasts.

Aleuroplast: The protein containing leucoplasts are called aleuroplasts.

On this page, you will find Structure of the Atom Class 9 Notes Science Chapter 4 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 4 Structure of the Atom will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 4 Notes Structure of the Atom

Structure of the Atom Class 9 Notes Understanding the Lesson

1. Discovery of electron: Study of cathode rays.

• On electrical discharge through gases at very low pressure, cathode rays are produced.
• Cathode rays move in straight line.
• Cathode rays have some mechanical energy.
• Cathode rays consist of negatively charged particles, i.e., electrons.

2. Electron: An electron is the sub-atomic or fundamental particle which carries one unit negative charge.
It is represented by e^–.
Mass of one electron = 9.11 x 10^-31 kg.
Charge of one electron = – 1.6 x 10^-19 C.

3. Proton: Discovered by Goldstein (1886) anode ray or canal ray experiment.
Mass of proton = 1.67 x 10^-24 kg.
One proton is 1840 times heavier than electron.
Charge on proton = + 1.6 x 10^-19 C.

4. Thomson’s model of an atom
He proposed that:

• An atom consists of a uniform sphere of positive electricity in which the electrons are distributed more or less uniformly.
• The negative and the positive charge are equal in magnitude. Thus, the atom as a whole is electrically neutral.

5. Rutherford’s model of an atom
Rutherford observed that:

• Most of the a-particles (nearly 99%) passed through the gold foil undeflected.
• Some of the a-particles (about one in every 20,000) were deflected by small angles.
• A few particles (1 in about 10⁶) were either deflected by very large angles or were actually reflected back along their path.

In order to explain the observation of his scattering experiment, Rutherford assumed that the solid gold foil consists of layers of individual atoms touching each other so that there is hardly any empty space between them. Rutherford explained his observation as follows:

• Most of the space inside the atom is empty because most of the a-particles passed through the gold foil without getting deflected.
• Very few particles were deflected from their path, indicating that the positive charge of the atom occupies very little space
• A very small fraction of a-particles was deflected by 180°, indicating that all the positive charge and mass of the gold atom were, concentrated in a very small volume within the atom.

On the basis of his experiment, Rutherford put forward the nuclear model of an atom, which had the following features:

• There is a positively charged centre in an atom called the nucleus. Nearly all the mass of an atom resides in the nucleus.
• The electrons revolve around the nucleus in circular paths.
• The size of the nucleus is very small as compared to the size of the atom.

6. Drawbacks of Rutherford’s model of the atom
Rutherford’s model could not explain the stability of the atom. This is because according to Rutherford’s model, an atom consists of a small heavy positively charged nucleus in the centre and the electrons revolve around it.

However, whenever a charged particle like an electron revolves around a central force like that of a nucleus, it loses energy continuously in the form of radiations. Thus, the orbit of the revolving electron will keep on becoming smaller and smaller and ultimately the electron should fall into the nucleus.

7. Discovery of Neutrons
Neutron may be defined as subatomic particle which had no charge and a mass nearly equal to that of proton:

• Mass of neutron = 1.676 x 10^-24
• Charge of neutron = 0 (zero).

8. Bohr’s atomic model

• Electron revolves around nucleus only in certain selected circular orbits with definite energies and are called energy shells or energy levels.
• While revolving around the nucleus in an orbit, an electron does not lose energy nor does it gain energy.
• Different shells or orbits are numbered as 1, 2, 3, 4…………………… or designated as K, L, M, N……………….
• Every orbit is associated with a fixed amount of energy, so on gaining a certain amount of energy e~, jumps to the higher orbit.

9. How are electrons distributed in different orbit (shells)?
Answer:
The distribution of the electrons in the shells is known as electronic configuration. It is based on certain guide­lines or rules given by Bohr and Bury. This is known as Bohr-Bury scheme. According to this scheme,

1. The maximum number of electrons present in a shell is given by the formula 2n², where ‘n’ is the orbit number of energy level index, 1, 2. 3,………………… Hence the maximum number of electrons in different shells are as follows:

• First orbit or K-shell will be = 2 x 1² = 2,
• Second orbit or L-shell will be = 2 x 2² = 4,
• Third orbit or M-shell will be = 2 x 3² = 18,
• Fourth orbit or N-shell will be = 2 x 4² = 32 and so on.

3. The maximum number of electrons that can be accommodated in the outermost orbit is 8.

4. Electrons are not accommodated in a given shell, unless the inner shells are filled. That is, the shells are filled in a step-wise manner.
Atomic structure of first eighteen elements is shown schematically in the figure given below.

10. Valency
The electrons present in the outermost shell of an atom are known as the valence electrons.
From the Bohr-Bury scheme, the outermost shell of the an atom can accommodate a maximum of 8 electrons. The combining capacity or valency of elements having a completely filled outermost shell is zero. Inert elements, like helium atom has two electrons in its outermost shell and all other elements have atoms with eight electrons in their outermost shell.

The combining capacity of the atoms of other elements was explained in terms of their tendency to attain a fully-filled outermost shell (stable octect or dulpet). The atoms which do not have their outermost shell fully filled enter into bond formation with other atoms in order to achieve an octet (or duplet) of electrons in their outermost shells. They do so either by sharing, losing or gaining electrons.

If the number of electrons in the outermost shell of an atom is close to its full capacity, then valency is determined in a different way.

11. Atomic number (Z)
The number of unit positive charges present in the nucleus of an atom is known as atomic number of the element.
It is denoted by the symbol Z.
Atomic no. (Z) = No. of protons = No. of electrons.
For example: Hydrogen, Z = 1 because in hydrogen atom, only one proton is present in the nucleus.
Similarly, for carbon Z = 6.

12. Mass number
The mass number is defined as the sum of the total number of protons and neutrons present in the nucleus of an atom. For example, mass of carbon is 12u because it has 6 protons and 6 neutrons, 6u + 6u = 12u. Similarly, the mass of aluminium is 27u because it has 13 protons and 14 neutrons.

The atomic number, mass number and symbol of the element are to be written as:

For example: Nitrogen is written as \({ }_{7}^{14} \mathrm{N}\).

13. Isotopes
The different atoms of the same element having same atomic number but different mass numbers.
For example: Hydrogen atom, has three isotopes, namely protium \(\left({ }_{1}^{1} \mathrm{H}\right)\), deuterium and tritium \(\left({ }_{1}^{3} \mathrm{H} \text { or } \mathrm{T}\right)\)

14. Applications of isotopes:

• An isotope of Uranium (U-235) is used as a fuel in nuclear reactors.
• An isotope of cobalt (C-60) is used in treatment of cancer by radiation therapy.
• An isotope of iodine is used in the treatment of goitre.
• Ages of old wooden articles are determined by observing the radioactivity of C-14 isotope of carbon.

15. Isobars:
Atoms of different elements with different atomic numbers which have the same mass number are known as isobars.

For example: Two elements – calcium, atomic number 20, and argon, atomic number 18 are isobars. The number of electrons in these atoms is different, but the mass number of both of these elements is 40.

Class 9 Science Chapter 4 Notes Important Terms

Cathode rays: It consist of negatively charged particles (electrons) emitted by passing electricity through gases at low pressure.

Anode rays: These rays are produced along with cathode rays and move towards cathode. They consist of positively charged ions.

Electrons: Electrons are fundamental particles carrying a unit negative charge and are a common constituent of all atoms.

Protons: (This positively charged particle was characterised in 1919). The fundamental particle which carries one unit of positive charge and has a mass nearly equal to that of an H-atom. Mass of proton = 1.6726 x 10^-24 g.

Neutron: The fundamental particle, which has a mass nearly equal to that of an H atom but has no charge.
Mass of neutron = 1.6749 x 10^-24 g.

Valency: It is the capacity of atoms of a given element to combine with, or replace atoms of hydrogen. In HCl gas, valency of chlorine is 1.

Nucleons: Protons and neutrons together are known as nucleons.

Isobars: Atoms having the same mass number but different atomic numbers.
For example, K – 40 and Ar – 40.

Isotopes: Atoms with identical atomic number but different mass numbers.
For example,\({ }_{1}^{1} \mathrm{H},{ }_{1}^{2} \mathrm{H} \text { and }{ }_{1}^{3} \mathrm{H}\)

On this page, you will find NCERT Class 9 History Chapter 6 Notes Pdf free download. CBSE Class 9 Social Science Notes History Chapter 6 SST Peasants and Farmers will seemingly, help them to revise the important concepts in less time.

Peasants and Farmers Class 9 Notes Social Science History Chapter 6

CBSE Class 9 History Chapter 6 Notes Understanding the Lesson

1. This lesson deals with the small cottages in England, the wheat farmers of the USA, and the opium producers of Bengal and what happened to them with the coming to modern agriculture.

2. It is England where the agriculture revolution first occurred. Over the late eighteenth and early nineteenth centuries the English countryside changed dramatically.

3. Before this time in large parts of England the countryside was open where peasants cultivated, pastured their cows and grazed their sheep. For the poor, the common land was essential for survival.

4. But their life change miserably when common land began to be enclosed. Rich farmers drove them out and prevented them from entering the enclosed fields.

5. The early enclosures were usually created by individual landlords. They were not supported by the state or the church. After the mid-eighteenth century, however the enclosure movement swept through the countryside, changing the English landscape forever. The British Parliament legalized these enclosures.

6. Unlike the early enclosures that promoted sheep farming, the land being enclosed in the late eighteenth century was for grain production to feed the growing population.

7. Landlords were encouraged to enclose lands and enlarge the area under grain cultivation. Farmers at this time continued to use the simple innovations in agriculture that had become common by the early eighteenth century.

8. Enclosures allowed the richer landowners to expand the land under their control and produce more for the market. But it worsened the condition of the poor. They could no longer collect their firewood from the forests, or graze their cattle on the commons.

9. In places where enclosures happened on an extensive scale—the poor were displaced from the land. They found their customary rights gradually disappearing. Deprived of their rights and driven off the land, they wandered in search of work.

10. The introduction of threshing machines increased the miseries of the poor. The rich farmers bought the new threshing machines that had come into the market. This reduced their dependence on laborers. As a result, their income became instable, their jobs insecure, their livelihood precarious. For them the threshing machines had become a sigh of bad times.

11. At the time that common fields were being enclosed in England at the end of the eighteenth century, settled agriculture had not developed on any extensive scale in the USA. Forests covered over 800 millions acres and grasslands 600 million acres.

12. By the early nineteenth century, this landscape had transformed radically. White Americans had moved westward and established control upto the west coast, displacing local tribes and carving out the entire landscape into different agricultural belts.

13. The story of agrarian expansion is closely connected to the westward movement of the white settlers who took over the land. After the American War of Independence from 1775 to 1783 and the formation of the United States of America, the white Americans began to move westward and turn forests into cultivated fields.

14. From the late nineteenth century, wheat production expanded in the USA dramatically. By the early twentieth century about 45 million acres of land in the USA was under wheat. The area soon expanded to 74 million acres. This dramatic expansion was made possible by new technological innovations such as mechanical reapers, drills, tractors, etc.

15. For the poorer farmers, machines brought miseries. They became jobless because mechanization had reduced the need for labour. The boom of the late nineteenth and early twentieth centuries came to an end by the mid-1920s. There was large surplus wheat which lowered down its prices.

16. The expansion of wheat agriculture in the Great Plains created ecological problems too because zealous farmers had recklessly uprooted all vegetation, and tractors had turned the soil over, and broken the sod into dust. In the early twentieth century, the whole region had become a dust bowl.

17. In the colonial period, rural India produced a range of crops for the world market. In the early nineteenth century, indigo and opium were two of the major commercial crops. By the end of the century, peasants were producing sugar cane, cotton, jute, wheat and several other crops for export.

18. The history of opium production in India was linked up with the story of British trade with China. In the late eighteenth century, the English East India Company was buying tea and silk from China for sale in England. As tea became a popular English drink, the trade became very important.

19. But there was a problem. England at this time produced nothing that could be easily sold in China. Opium, they thought, could be sold in China so they persuaded Indian farmers to grow this commodity.

20. They introduced system of advances to trap the poor farmers of Bengal and Bihar. When offered a loan, they readily accepted it, hoping to meet their immediate needs and pay back the loan at a later stage. But the loan tied the peasants to the headmen and through him to the government.

21. By taking the loan, the cultivator was forced to grow opium on a specified area of land and handover the produce to the agents once the crop had been harvested. Here, it is worth mentioning that the prices given to the peasants were very low.

Peasants and Farmers Class 9 CBSE Notes Important Terms

Bushel: A measure of capacity.

Shillings: An English currency. (20 shillings = £ 1)

Commons: Land or resources belonging to or affecting the whole of a community.

Sod: Pieces of earth with grass.

Maund: A measure of weight. (1 maund = 40 seers. 1 seer is a little under a kg))

Opium: The dried latex obtained from the opium poppy.

Scythe: A machine used for mowing grass.

Agrarian: Relating to cultivated land or the cultivation of land.

Enclosure: An area that is surrounded by a barrier.

On this page, you will find NCERT Class 9 History Chapter 5 Notes Pdf free download. CBSE Class 9 Social Science Notes History Chapter 5 SST Pastoralists in the Modern World will seemingly, help them to revise the important concepts in less time.

Pastoralists in the Modern World Class 9 Notes Social Science History Chapter 5

CBSE Class 9 History Chapter 5 Notes Understanding the Lesson

1. Pastoralism has been important in societies like India and Africa. Here we will read about the way colonialism impacted their lives, and how they have coped with the pressures of modern society. Pastoralism in India-Pastoralists are found in mountains, plateaus, plains and deserts of India. In the mountains of Jammu and Kashmir are found the Gujjar Bakarwals. They are great herders of goat and sheep.

2. The Gaddi shepherds are found in Himachal Pradesh. Further to the east, in Garhwal and Kumaon, the Gujjar cattle herders can be seen.

3. These pastoral communities moved annually between their summer and winter grazing grounds. They had to adjust to seasonal changes and make effective use of available pastures in different places. When the pasture was exhausted or unusable in one place they moved their herds and flock to new areas.

4. Dhangars were an important pastoral community of Maharashtra. They stayed in the central plateau of Maharashtra during the monsoon, grew bajra and moved west by October. After a march of about one month they reached the Konkan where they lived till the onset of monsoon. Afterwards, they left the Konkan and the coastal areas with their flocks and returned to the settlements on the dry plateau.

5. In Karnataka and Andhra Pradesh, the dry central plateau was inhabited by cattle, goat and sheepherders. The Gollas herded cattle. The Kurumas and Kurubas reared sheep and goats and sold woven blankets.

6. Banjaras were well-known group of graziers. They were to be found in the villages of Uttar Pradesh, Punjab, Rajasthan, Madhya Pradesh and Maharashtra.

7. In the deserts of Rajasthan lived the Raikas. They combined cultivation with pastoralism. One group of Raikas-known as the Maru (desert) Raikas-herded camels and another group reared sheep and goat.

8. The life of pastoralists changed dramatically during the colonial rule. Their grazing grounds shrank, their movements were regulated, and the revenue they had to pay increased.

9. The colonial government enacted Forest Acts which prevented pastoralists from entering many forests that had earlier provided valuable forage for their cattle.

10. The British officials were suspicious of nomadic people. Since they kept on moving from one place to another, they were considered to be criminal. In 1871, the colonial government in India passed the Criminal Tribes Act to check their movement.

11. As pasturelands were turned into cultivated fields, the existing animal stock had to feed on whatever grazing land remained. This led to continuous intensive grazing of these pastures. As a result of this the quality of pastures declined. This in turn created a further shortage of forage for animals and the deterioration of animal stock.

12. Some pastoralists reduced the number of cattle in their herds, because there was dearth of enough pastures. Others discovered new pastures when movement to old grazing grounds became difficult. And thus, pastoralists continue to survive. In many regions their numbers have also expanded over recent decades.

13. Pastoralism in Africa-Over half the world’s pastoral population lives in Africa. Even today, over 22 million Africans depend on some form of pastoral activity for their livelihood. They include communities like Bedouins, Berbers, Maasai, Somali, Boran and Turkana.

14. Like pastoralists in India, the lives of African pastoralists have changed dramatically over the colonial and post-colonial periods. We can take example of one pastoral community-the Maasai-whose life changed when new laws and regulations were imposed on them by the colonial government.

15. The Maasai cattle herders live primarily in east Africa in Kenya and Tanzania. Before colonial times, Maasai land stretched over a vast area from north Kenya to the steppes of northern Tanzania. In the late nineteenth century, their best grazing lands were gradually taken over for white settlement and they were pushed into a small area in south Kenya and north Tanzania.

16. From the late nineteenth century, the British colonial government in east Africa also encouraged local peasant communities to expand cultivation. As a result, pasturelands were turned into cultivated fields. Large areas of grazing land were also turned into game reserves like the Maasai Mara and Samburu National Park in Kenya and Serengeti Park in Tanzania.

17. The loss of the finest grazing lands and water resources created pressure on the small area of land that the Maasai were confined within. Continuous grazing within a small area deteriorated the quality of pastures.

18. Like the Maasai, other pastoral groups were also forced to live within the confines of special reserves. The boundaries of these reserves became the limits within which they could now move.

19. The new territorial boundaries and restrictions imposed on them suddenly changed the loves of pastoralists. This adversely affected their pastoral and trading activities.

20. Pastoral communities in different parts of the world are affected in a variety of different ways by changes in the modem world. New laws and new borders affect the patterns of their movement. Yet, they do adapt to new times. They change the paths of their annual movement and reduce their cattle number but at the same time also demand a right in the management of forests and water resources.

Pastoralists in the Modern World Class 9 CBSE Notes Important Terms

Nomads: People who do not live in one place but move from one area to another to earn their living.

Pastoralism: The branch of agriculture concerned with the raising of livestock. It is animal | husbandry: the care, tending and use of animals such as camels, goats, cattle, etc.

Kafila: When several households come together for a journey, it is known as

Bhabar: A dry forested area below the foothills of Garhwal and Kumaun.

Bugyal: Vast meadows in the high mountains.

Kharif: The autumn crop, usually harvested between September and October.

Rabi: The spring crop, usually harvested after March.

Stubble: Lower ends of grain stalks left in the ground after harvesting.

Customary rights: Rights that people are used to by custom and tradition.

Livestock: Cattle, goats and sheep.

Drought: A period of below-average precipitation in a given region, resulting in prolonged shortages in its water supply.

Forage: Plant material (mainly plant leaves and stems) eaten by grazing livestock.