Category: ICSE

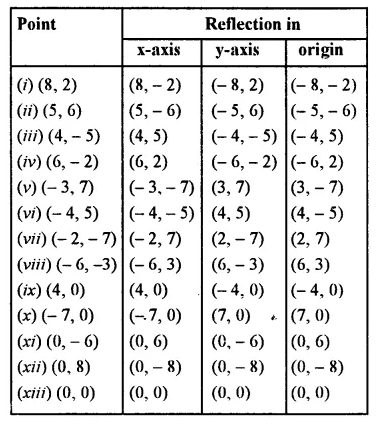
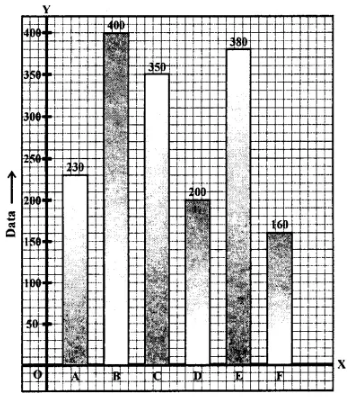
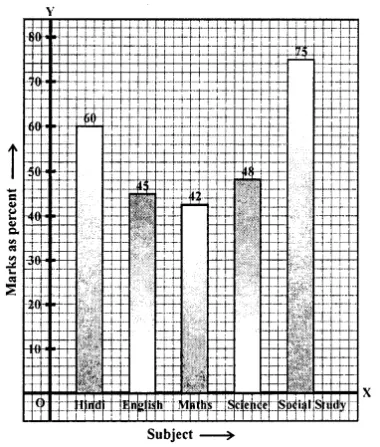
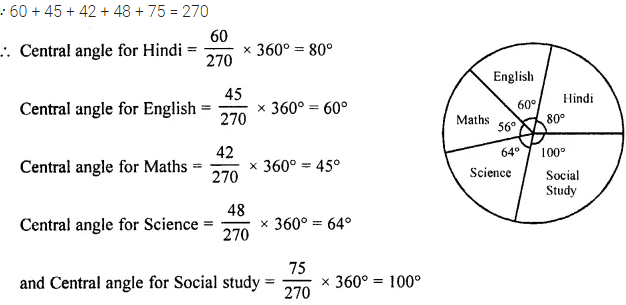
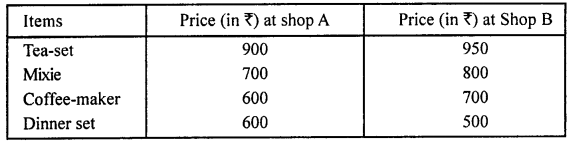
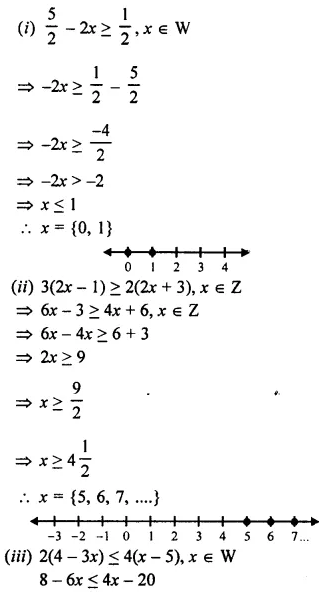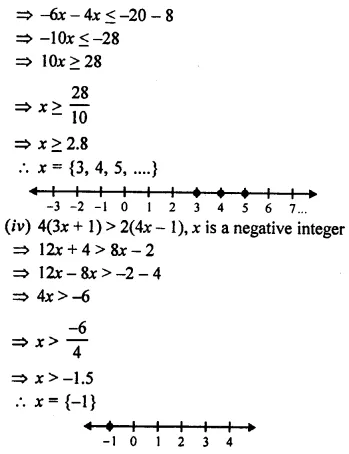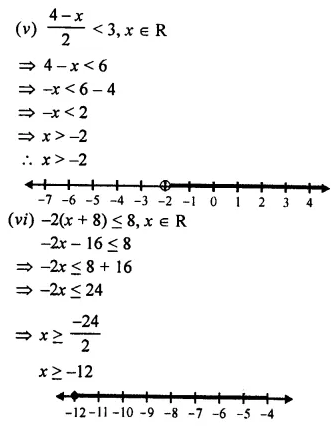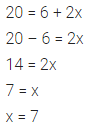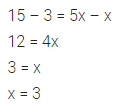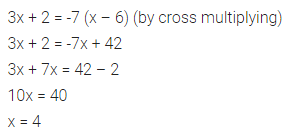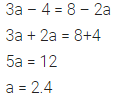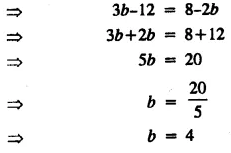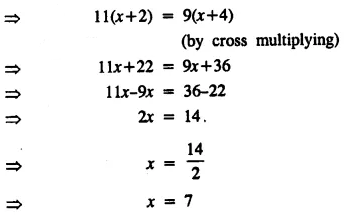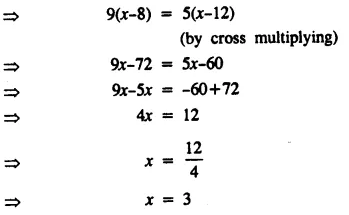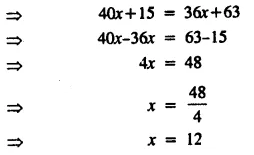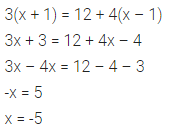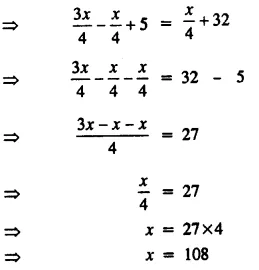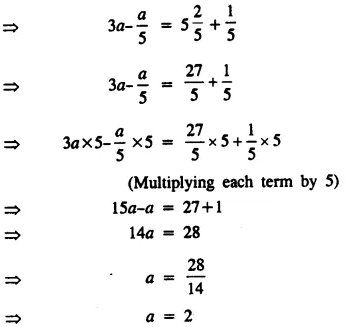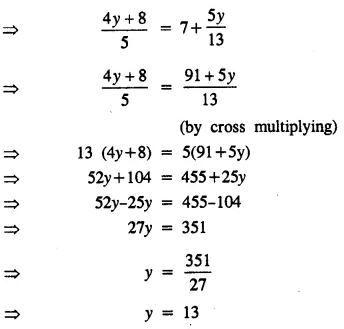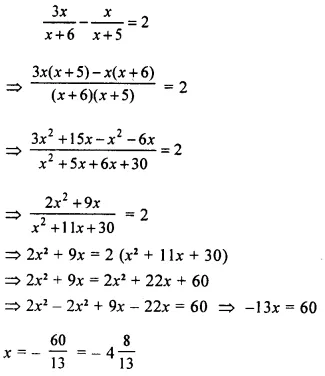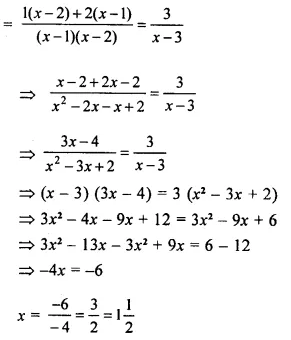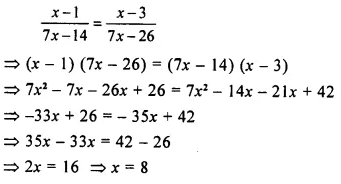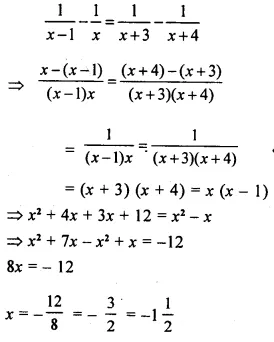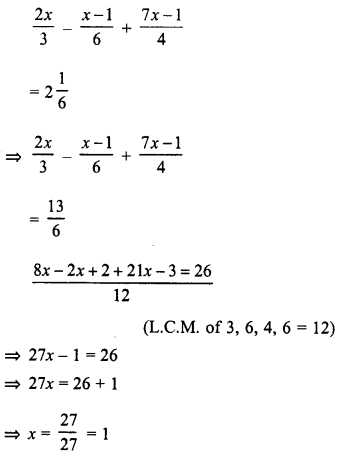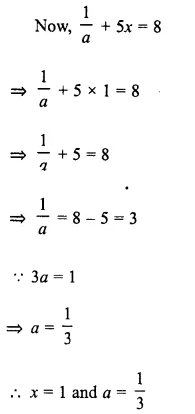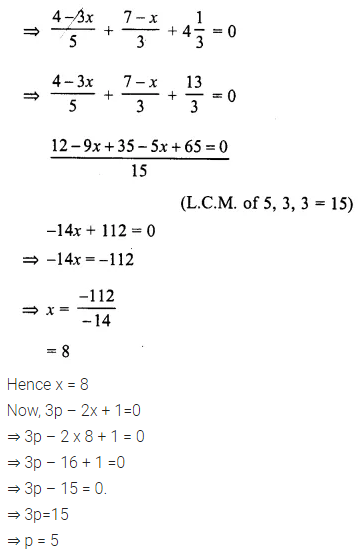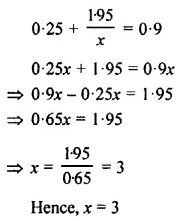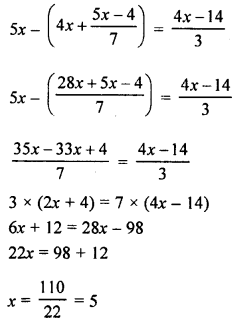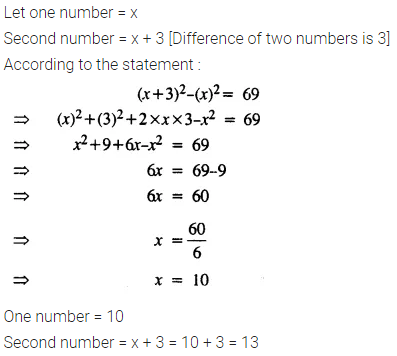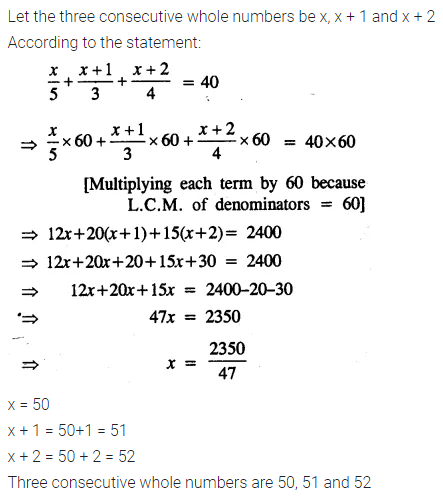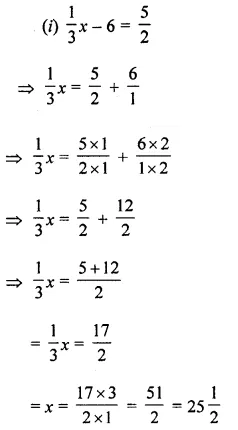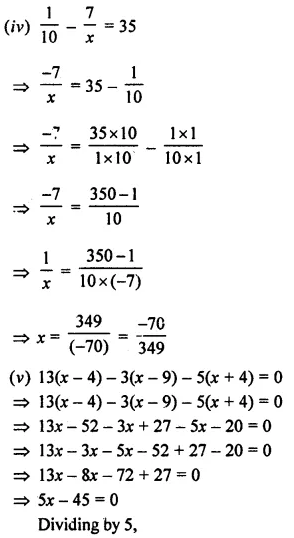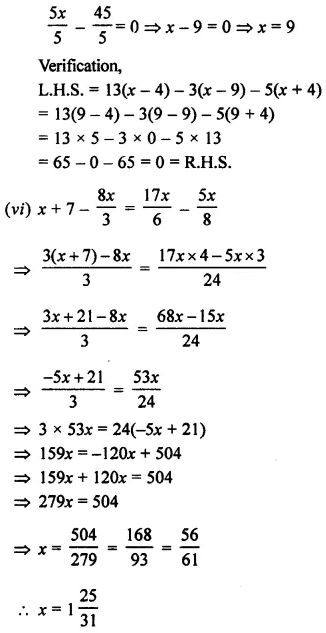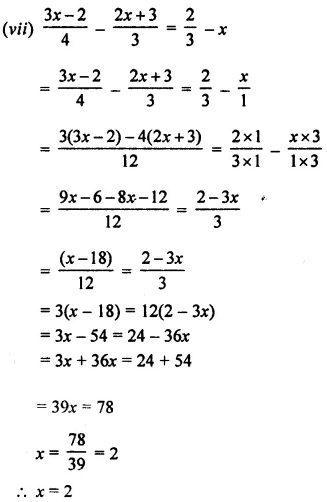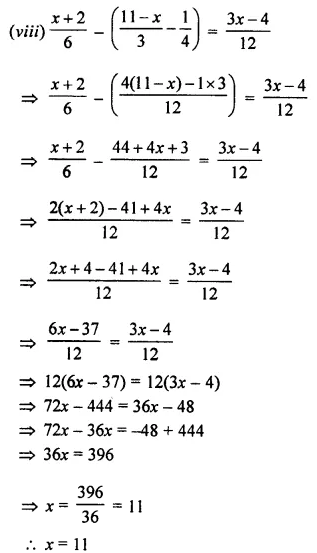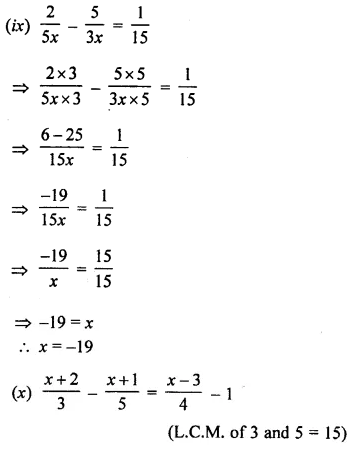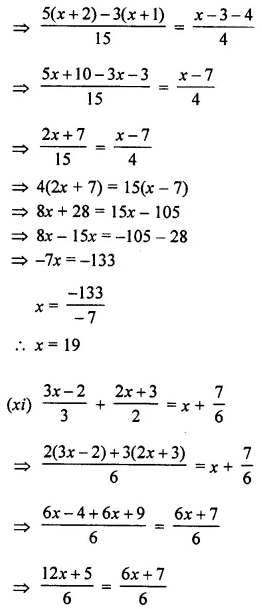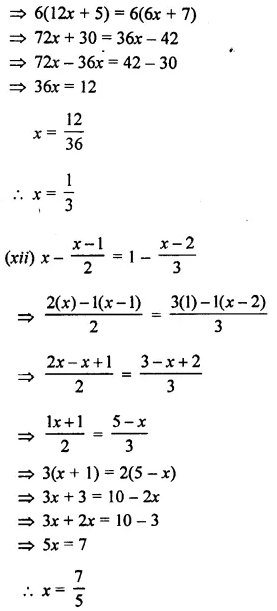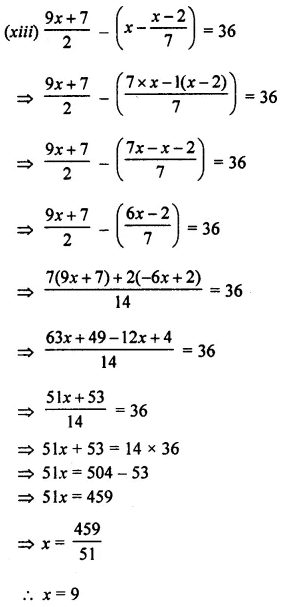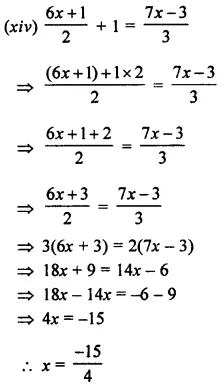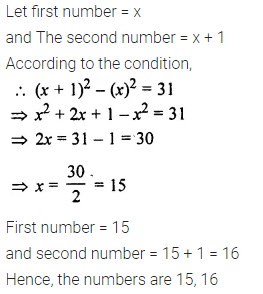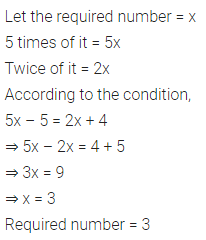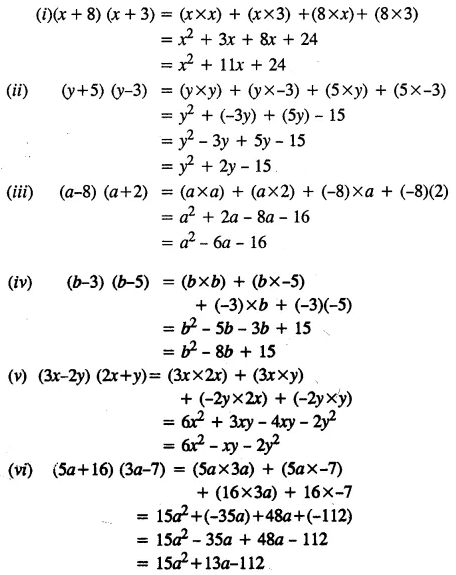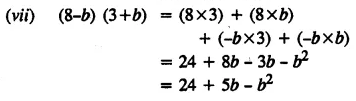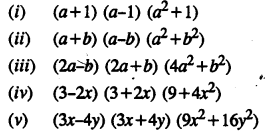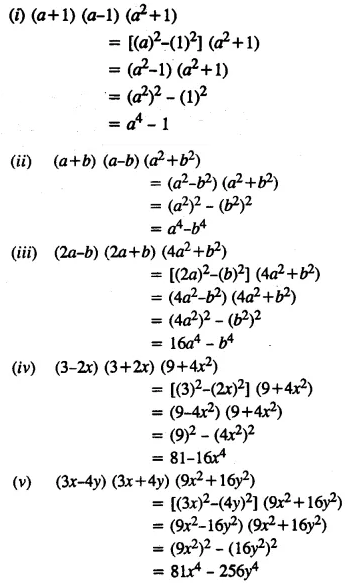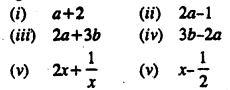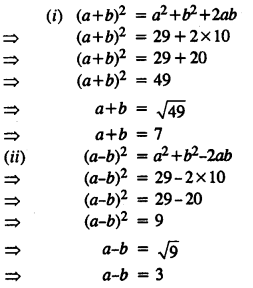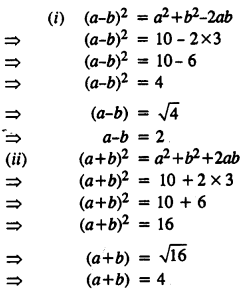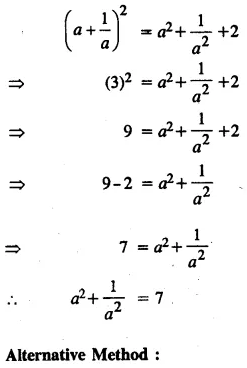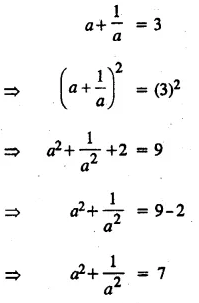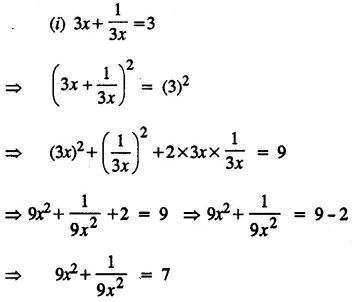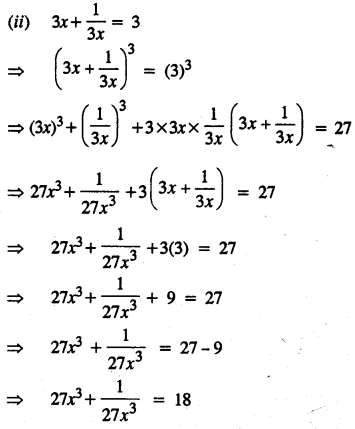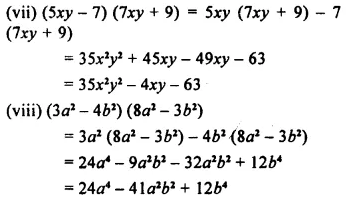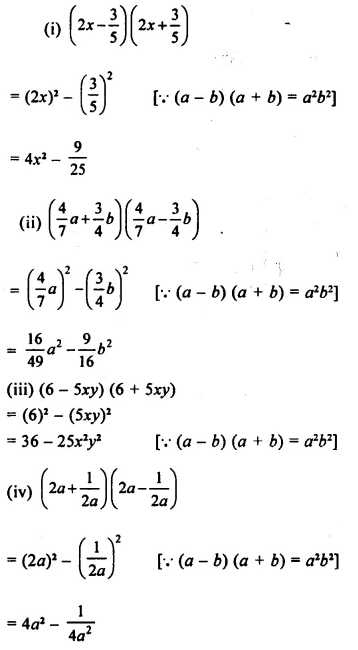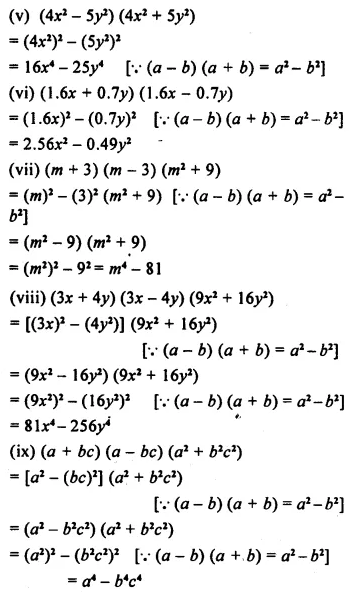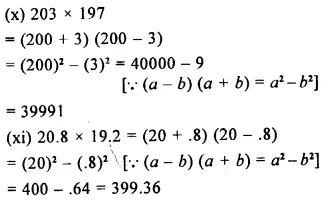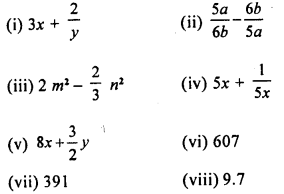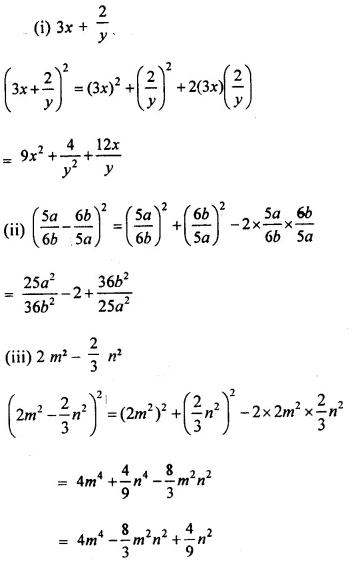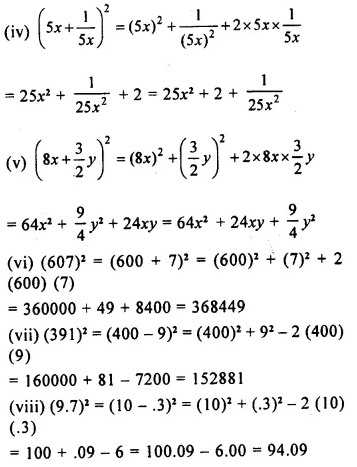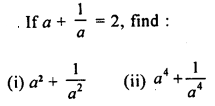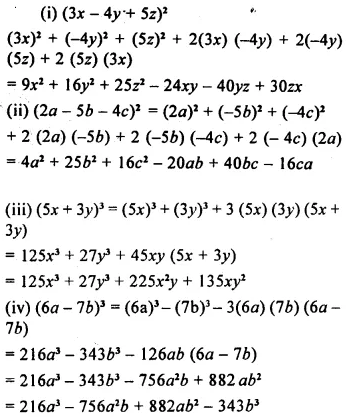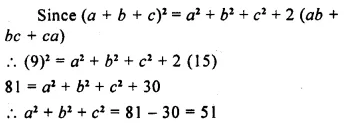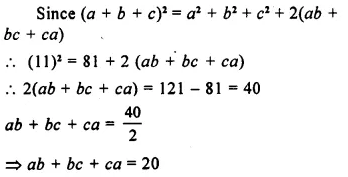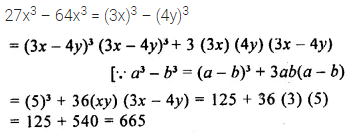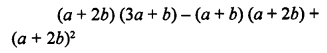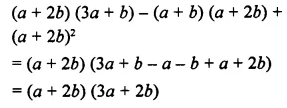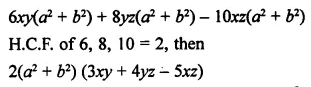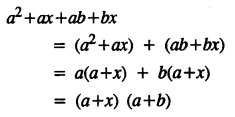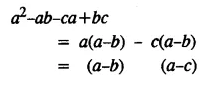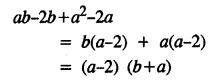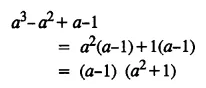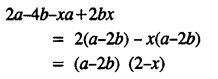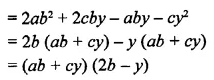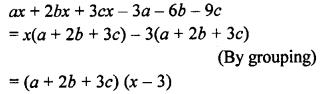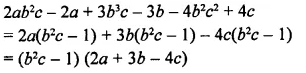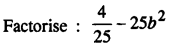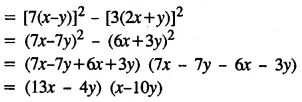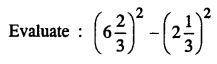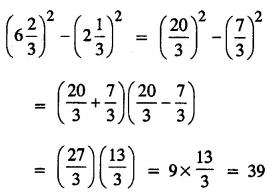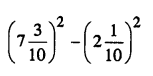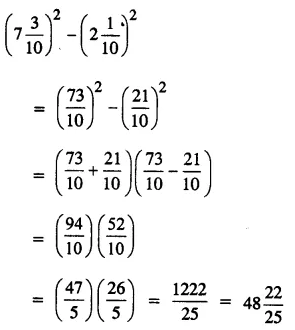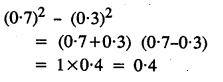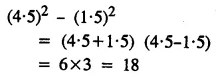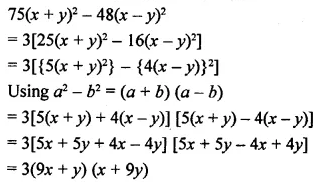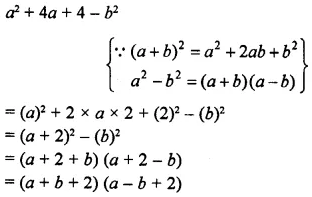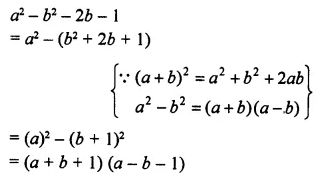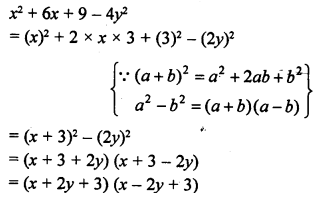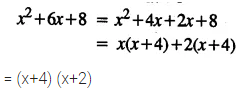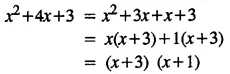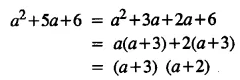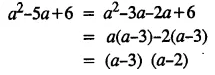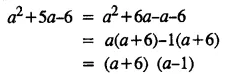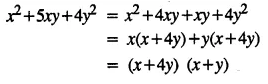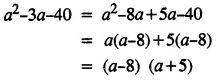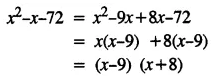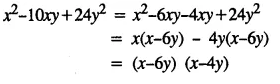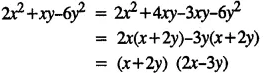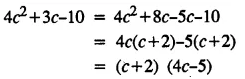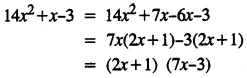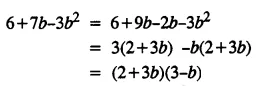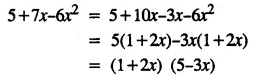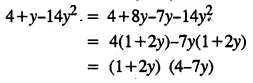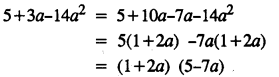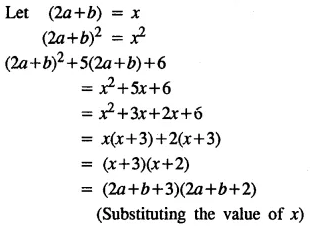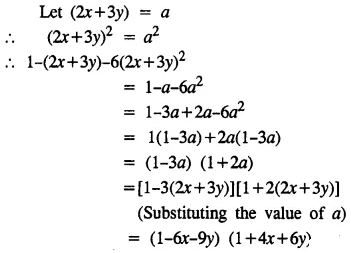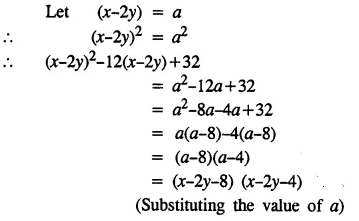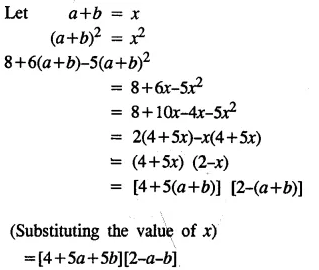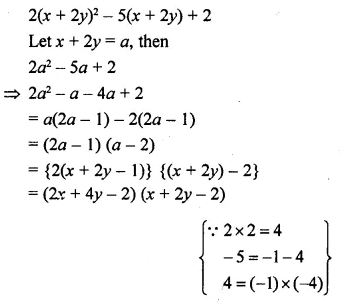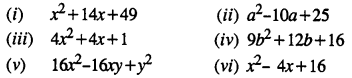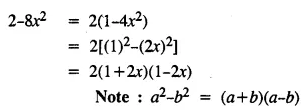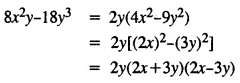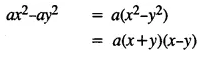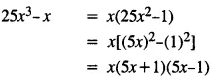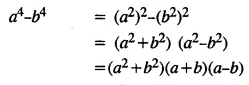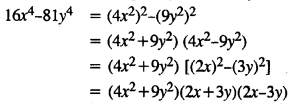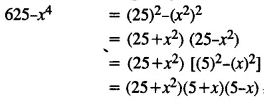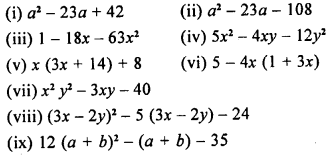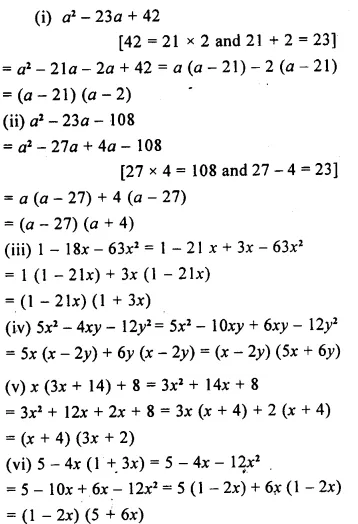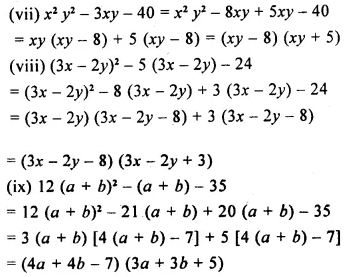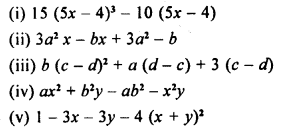Selina Concise Mathematics Class 8 ICSE Solutions Chapter 15 Linear Inequations (Including Number Lines)

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 15 Linear Inequations (Including Number Lines)

Linear Inequations Exercise 15A – Selina Concise Mathematics Class 8 ICSE Solutions

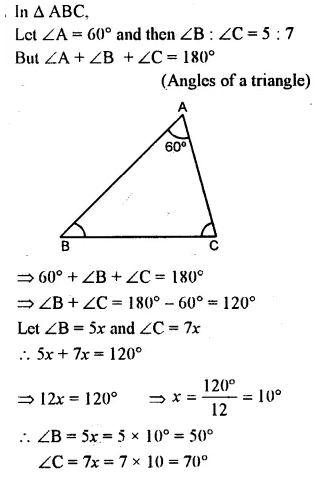
Question 1.
If the replacement set is the set of natural numbers, solve.
(i) x – 5 < 0
(ii) x + 1 < 7
(iii) 3x – 4 > 6
(iv) 4x + 1 > 17
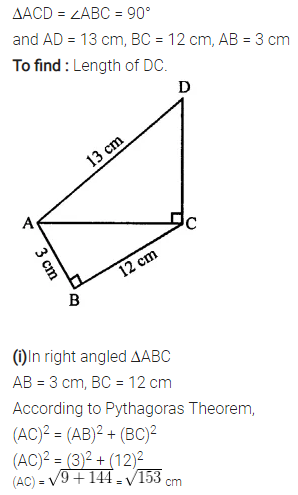
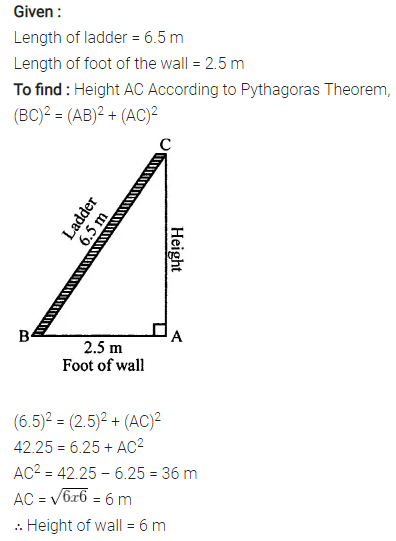
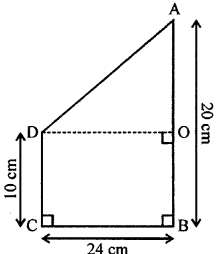
Solution:

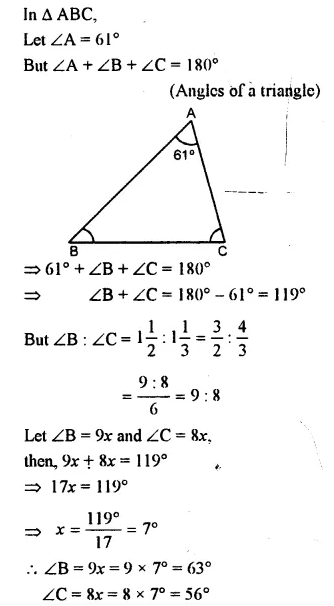
Question 2.
If the replacement set = {-6, -3, 0, 3, 6, 9}; find the truth set of the following:
(i) 2x – 1 > 9
(ii) 3x + 7 < 1
Solution:

Question 3.
Solve 7 > 3x – 8; x ∈ N
Solution:

Question 4.
-17 < 9y – 8 ; y ∈ Z
Solution:

Question 5.
Solve 9x – 7 ≤ 28 + 4x; x ∈ W
Solution:

Question 6.
Solve : \(\frac { 2 }{ 3 }\)x + 8 < 12 ; x ∈ W
Solution:

Question 7.
Solve -5 (x + 4) > 30 ; x ∈ Z
Solution:

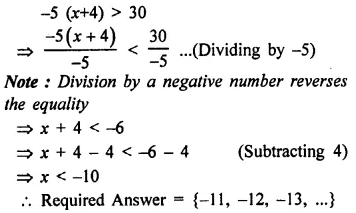
Question 8.
Solve the inquation 8 – 2x > x – 5 ; x ∈ N.
Solution:

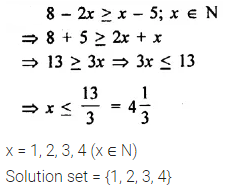
Question 9.
Solve the inequality 18 – 3 (2x – 5) > 12; x ∈ W.
Solution:

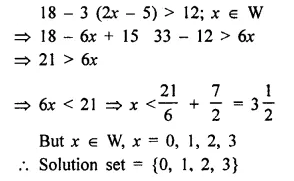
Question 10.
Solve : \(\frac { 2x+1 }{ 3 }\) + 15 < 17; x ∈ W.
Solution:

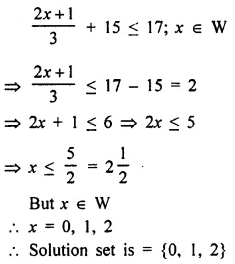
Question 11.
Solve : -3 + x < 2, x ∈ N
Solution:

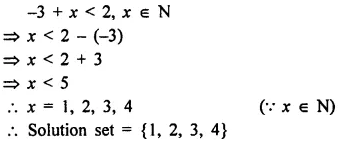
Question 12.
Solve : 4x – 5 > 10 – x, x ∈ {0, 1, 2, 3, 4, 5, 6, 7}
Solution:

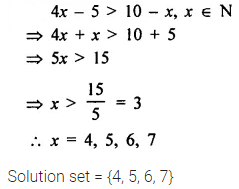
Question 13.
Solve : 15 – 2(2x – 1) < 15, x ∈ Z.
Solution:

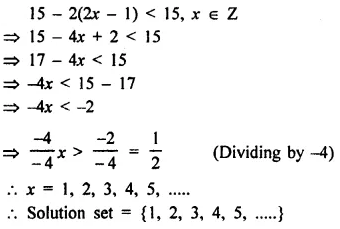
Question 14.
Solve : \(\frac { 2x+3 }{ 5 }\) > \(\frac { 4x-1 }{ 2 }\) , x ∈ W.
Solution:

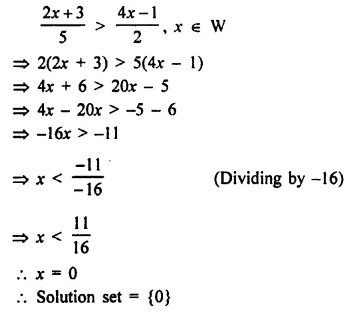
Linear Inequations Exercise 15B – Selina Concise Mathematics Class 8 ICSE Solutions

Solve and graph the solution set on a number line :
Question 1.
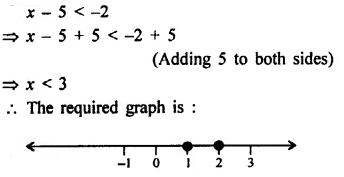
x – 5 < -2 ; x ∈ N
Solution:

Question 2.
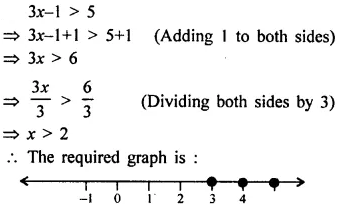
3x – 1 > 5 ; x ∈ W
Solution:

Question 3.
-3x + 12 < -15 ; x ∈ R.
Solution:

Question 4.
7 > 3x – 8 ; x ∈ W
Solution:

Question 5.
8x – 8 < – 24 ; x ∈ Z
Solution:

Question 6.
8x – 9 > 35 – 3x ; x ∈ N
Solution:

Question 7.
5x + 4 > 8x – 11 ; x ∈ Z
Solution:

Question 8.
\(\frac { 2x }{ 5 }\) + 1 < -3 ; x ∈ R
Solution:

Question 9.
\(\frac { x }{ 2 }\) > -1 + \(\frac { 3x }{ 4 }\) ; x ∈ N
Solution:

Question 10.
\(\frac { 2 }{ 3 }\) x + 5 ≤ \(\frac { 1 }{ 2 }\) x + 6 ; x ∈ W
Solution:

Question 11.
Solve the inequation 5(x – 2) > 4 (x + 3) – 24 and represent its solution on a number line.
Given the replacement set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Solution:

Question 12.
Solve \(\frac { 2 }{ 3 }\) (x – 1) + 4 < 10 and represent its solution on a number line.
Given replacement set is {-8, -6, -4, 3, 6, 8, 12}.
Solution:

Question 13.
For each inequation, given below, represent the solution on a number line :
(i) \(\frac { 5 }{ 2 }\) – 2x ≥ \(\frac { 1 }{ 2 }\) ; x ∈ W
(ii) 3(2x – 1) ≥ 2(2x + 3), x ∈ Z
(iii) 2(4 – 3x) ≤ 4(x – 5), x ∈ W
(iv) 4(3x + 1) > 2(4x – 1), x is a negative integer
(v) \(\frac { 4 – x }{ 2 }\) < 3, x ∈ R
(vi) -2(x + 8) ≤ 8, x ∈ R
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 17 Symmetry (Including Reflection and Rotation)

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 17 Symmetry (Including Reflection and Rotation)

Symmetry Exercise 17A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
For each figure, given below, draw the line (s) of symmetry, if possible :

Solution:

Question 2.
Write capital letters A to Z of English alphabet ; and in each case, if possible, draw the largest number of lines of symmetry.
Solution:

Question 3.
By drawing a free hand sketch of each of the following, draw in each case, the line (s) of symmetry,
if any:
(i) a scalene triangle
(ii) an isosceles right angled triangle
(iii) a rhombus
(iv) a kite shaped figure triangle.
(v) a rectangle
(vi) a square
(vii) an isosceles
Solution:

Question 4.
Draw a triangle with :
(i) no line of symmetry,
(ii) only one line of symmetry,
(iii) exactly two lines of symmetry,
(iv) exactly three lines of symmetry,
(v) more than three lines of symmetry.
In each case, if possible, represent the line/ lines of symmetry by dotted lines. Also, write the special name of the triangle drawn.
Solution:

Question 5.
Draw a quadrilateral with :
(i) no line of symmetry.
(ii) only one line of symmetry.
(iii) exactly two lines of symmetry.
(iv) exactly three lines of symmetry.
(v) exactly four lines of symmetry.
(vi) more than four lines of symmetry.
In each case, if possible, represent the line/ lines of symmetry by dotted lines. Also, write the special name of the quadrilateral drawn.
Solution:

Question 6.
Construct an equilateral triangle with each side 6 cm. In the triangle drawn, draw all the possible lines of symmetry.
Solution:

Question 7.
Construct a triangle ABC in which AB = AC = 5cin and BC = 5.6 cm. If possible, draw its lines of symmetry.
Solution:

Question 8.
Construct a triangle PQR such that PQ = QR = 5 .5 cm and angle PQR = 90°. If possible, draw its lines of symmetry.
Solution:

Question 9.
If possible, draw a rough sketch of a quadrilateral which has exactly two lines of symmetry.
Solution:

Question 10.
A quadrilateral ABCD is symmetric about its diagonal AC. Name tire sides of this quadrilateral which are equal.
Solution:

Symmetry Exercise 17B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
In each figure, given below, find the image of the point P in the line AB :

Solution:

Question 2.
In each figure, given below, find the image of the line segment AB in the line PQ :

Solution:

Question 3.
Complete the following table :

Solution:

Question 4.
A point P (7,3)|is reflected in x-axis to point P’. The point P’ is further reflected in v-axis to point P” Find :
(i) the co-ordinates of P’
(ii) the co-ordinates of P”
(iii) the image of P (7, 3) in origin.
Solution:

Question 5.
A point A (- 5, 4) is reflected in y-axis to point B. The point B is further reflected in origin to point C. find :
(i) the co-ordinates of B
(ii) the co-ordinates of C
(iii) the image of A (- 5, 4) in x-axis.
Solution:

Question 6.
The point P (3, – 8) is reflected in origin to point Q. The Point Q is further reflected in x-axis to point R. Find :
(i) the co-ordinates of Q
(ii) the co-ordinates of R
(iii) the image of P (3, – 8) in y-axis.
Solution:

Question 7.
Each of the points A (3, 0), B (7, 0), C (- 8, 0), D (- 7, 0) and E (0, 0) is reflected in x-axis to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Solution:

Question 8.
Each of the points A (0, 4), B (0, 10), C (0, – 4), D (0, – 6) and E (0, 0) is reflected in y-axis to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Solution:

Question 9.
Each of the points A (0, 7), B (8. 0), C (0, -5), D (- 7, 0) and E (0, 0) are reflected in origin to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Solution:

Question 10.
Mark points A (4, 5) and B (- 5, 4) on a graph paper. Find A’, the image of A in x-axis and B’, the image of B in x-axis.
Mark A’ and B’ also on the same graph paper.
(ii) Join AB and A’ B’ and
find if AB = A’ B’ ?
Solution:

Question 11.
Mark points A (6, 4) and B (4, – 6) on a graph paper.
Find A’, the image of A in y-axis and B’, the image of B in y-axis. Mark A’ and B’ also on the same graph paper.
Solution:

Question 12.
Mark points A (- 6, 5) and B (- 4, – 6) on a graph paper. Find A’, the image of A in origin and B’, the image of B in origin. Mark A’ and B’ also on the same graph paper. Join AB and A’ B’. Is AB = A’ B’ ?
Solution:

Symmetry Exercise 17C – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
How many lines of symmetry does a rhombus have?
Solution:

Question 2.
What is the order of rotational symmetry of a rhombus?
Solution:

Question 3.
Show that each of the following figures has two lines of symmetry and a rotational.

Solution:

Question 4.
Name a figure that has a line of symmetry but does not have any roational symmetry.
Solution:

Question 5.
In each of the following figures, draw all possible lines of symmetry and also write the order of rotational symmetry:

Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 14 Linear Equations in one Variable (With Problems Based on Linear equations)

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 14 Linear Equations in one Variable (With Problems Based on Linear equations)

Linear Equations in one Variable Exercise 14A – Selina Concise Mathematics Class 8 ICSE Solutions

Solve the following equations:
Question 1.
20 = 6 + 2x
Solution:

Question 2.
15 + x = 5x + 3
Solution:

Question 3.
\(\frac { 3x+2 }{ x-6 }\) = -7
Solution:

Question 4.
3a – 4 = 2(4 – a)
Solution:

Question 5.
3(b – 4) = 2(4 – b)
Solution:

Question 6.
\(\frac { x+2 }{ 9 } =\frac { x+4 }{ 11 }\)
Solution:

Question 7.
\(\frac { x-8 }{ 5 } =\frac { x-12 }{ 9 }\)
Solution:

Question 8.
5(8x + 3) = 9(4x + 7)
Solution:

Question 9.
3(x + 1) = 12 + 4(x – 1)
Solution:

Question 10.
\(\frac { 3x }{ 4 } -\frac { 1 }{ 4 } \left( x-20 \right) =\frac { x }{ 4 } +32\)
Solution:

Question 11.
\(3a-\frac { 1 }{ 5 } =\frac { a }{ 5 } +5\frac { 2 }{ 5 }\)
Solution:

Question 12.
\(\frac { x }{ 3 } -2\frac { 1 }{ 2 } =\frac { 4x }{ 9 } -\frac { 2x }{ 3 }\)
Solution:

Question 13.
\(\frac { 4\left( y+2 \right) }{ 5 } =7+\frac { 5y }{ 13 }\)
Solution:

Question 14.
\(\frac { a+5 }{ 6 } -\frac { a+1 }{ 9 } =\frac { a+3 }{ 4 }\)
Solution:

Question 15.
\(\frac { 2x-13 }{ 5 } -\frac { x-3 }{ 11 } =\frac { x-9 }{ 5 } +1\)
Solution:

Question 16.
6(6x – 5) – 5 (7x – 8) = 12 (4 – x) + 1
Solution:

Question 17.
(x – 5) (x + 3) = (x – 7) (x + 4)
Solution:

Question 18.
(x – 5)² – (x + 2)² = -2
Solution:

Question 19.
(x – 1) (x + 6) – (x – 2) (x – 3) = 3
Solution:

Question 20.
\(\frac { 3x }{ x+6 } -\frac { x }{ x+5 } =2\)
Solution:

Question 21.
\(\frac { 1 }{ x-1 } +\frac { 2 }{ x-2 } =\frac { 3 }{ x-3 }\)
Solution:

Question 22.
\(\frac { x-1 }{ 7x-14 } =\frac { x-3 }{ 7x-26 }\)
Solution:

Question 23.
\(\frac { 1 }{ x-1 } -\frac { 1 }{ x } =\frac { 1 }{ x+3 } -\frac { 1 }{ x+4 }\)
Solution:

Question 24.
Solve: \(\frac { 2x }{ 3 } -\frac { x-1 }{ 6 } +\frac { 7x-1 }{ 4 } =2\frac { 1 }{ 6 }\)
Hence, find the value of ‘a’, if \(\frac { 1 }{ a }\) + 5x = 8.
Solution:

Question 25.
Solve: \(\frac { 4-3x }{ 5 } +\frac { 7-x }{ 3 } +4\frac { 1 }{ 3 } =0\)
Hence find the value of ‘p’ if 2p – 2x + 1 = 0
Solution:

Question 26.
Solve: \(0.25+\frac { 1.95 }{ x } =0.9\)
Solution:

Question 27.
Solve: \(5x-\left( 4x+\frac { 5x-4 }{ 7 } \right) =\frac { 4x-14 }{ 3 }\)
Solution:

Linear Equations in one Variable Exercise 14B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Fifteen less than 4 times a number is 9. Find the number.
Solution:

Question 2.
If Megha’s age is increased by three times her age, the result is 60 years. Find her age
Solution:

Question 3.
28 is 12 less than 4 times a number. Find the number.
Solution:

Question 4.
Five less than 3 times a number is -20. Find the number.
Solution:

Question 5.
Fifteen more than 3 times Neetu’s age is the same as 4 times her age. How old is she?
Solution:

Question 6.
A number decreased by 30 is the same as 14 decreased by 3 times the number; Find the number.
Solution:

Question 7.
A’s salary is same as 4 times B’s salary. If together they earn Rs.3,750 a month, find the salary of each.
Solution:

Question 8.
Separate 178 into two parts so that the first part is 8 less than twice the second part.
Solution:

Question 9.
Six more than one-fourth of a number is two-fifth of the number. Find the number.
Solution:

Question 10.
The length of a rectangle is twice its width. If its perimeter is 54 cm; find its length.
Solution:

Question 11.
A rectangle’s length is 5 cm less than twice its width. If the length is decreased by 5 cm and width is increased by 2 cm; the perimeter of the resulting rectangle will be 74 cm. Find the length and the width of the origi¬nal rectangle.
Solution:

Question 12.
The sum of three consecutive odd numbers is 57. Find the numbers.
Solution:

Question 13.
A man’s age is three times that of his son, and in twelve years he will be twice as old as his son would be. What are their present ages.
Solution:

Question 14.
A man is 42 years old and his son is 12 years old. In how many years will the age of the son be half the age of the man at that time?
Solution:

Question 15.
A man completed a trip of 136 km in 8 hours. Some part of the trip was covered at 15 km/hr and the remaining at 18 km/hr. Find the part of the trip covered at 18 km/hr.
Solution:

Question 16.
The difference of two numbers is 3 and the difference of their squares is 69. Find the numbers.
Solution:

Question 17.
Two consecutive natural numbers are such that one-fourth of the smaller exceeds one-fifth of the greater by 1. Find the numbers.
Solution:

Question 18.
Three consecutive whole numbers are such that if they are divided by 5, 3 and 4 respectively; the sum of the quotients is 40. Find the numbers.
Solution:

Question 19.
If the same number be added to the numbers 5, 11, 15 and 31, the resulting numbers are in proportion. Find the number.
Solution:

Question 20.
The present age of a man is twice that of his son. Eight years hence, their ages will be in the ratio 7 : 4. Find their present ages.
Solution:

Linear Equations in one Variable Exercise 14C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Solve:
(i) \(\frac { 1 }{ 3 } x-6=\frac { 5 }{ 2 }\)
(ii) \(\frac { 2x }{ 3 } -\frac { 3x }{ 8 } =\frac { 7 }{ 12 }\)
(iii) (x + 2)(x + 3) + (x – 3)(x – 2) – 2x(x + 1) = 0
(iv) \(\frac { 1 }{ 10 } -\frac { 7 }{ x } =35\)
(v) 13(x – 4) – 3(x – 9) – 5(x + 4) = 0
(vi) x + 7 – \(\frac { 8x }{ 3 } =\frac { 17x }{ 6 } -\frac { 5x }{ 8 }\)
(vii) \(\frac { 3x-2 }{ 4 } -\frac { 2x+3 }{ 3 } =\frac { 2 }{ 3 } -x\)
(viii) \(\frac { x+2 }{ 6 } -\left( \frac { 11-x }{ 3 } -\frac { 1 }{ 4 } \right) =\frac { 3x-4 }{ 12 }\)
(ix) \(\frac { 2 }{ 5x } -\frac { 5 }{ 3x } =\frac { 1 }{ 15 }\)
(x) \(\frac { x+2 }{ 3 } -\frac { x+1 }{ 5 } =\frac { x-3 }{ 4 } -1\)
(xi) \(\frac { 3x-2 }{ 3 } +\frac { 2x+3 }{ 2 } =x+\frac { 7 }{ 6 }\)
(xii) \(x-\frac { x-1 }{ 2 } =1-\frac { x-2 }{ 3 }\)
(xiii) \(\frac { 9x+7 }{ 2 } -\left( x-\frac { x-2 }{ 7 } \right) =36\)
(xiv) \(\frac { 6x+1 }{ 2 } +1=\frac { 7x-3 }{ 3 }\)
Solution:

Question 2.
After 12 years, I shall be 3 times as old as 1 was 4 years ago. Find my present age.
Solution:

Question 3.
A man sold an article for 7396 and gained 10% on it. Find the cost price of the article
Solution:

Question 4.
The sum of two numbers is 4500. If 10% of one number is 12.5% of the other, find the numbers.
Solution:

Question 5.
The sum of two numbers is 405 and their ratio is 8 : 7. Find the numbers.
Solution:

Question 6.
The ages of A and B are in the ratio 7 : 5. Ten years hence, the ratio of their ages will be 9 : 7. Find their present ages.
Solution:

Question 7.
Find the number whose double is 45 greater than its half.
Solution:

Question 8.
The difference between the squares of two consecutive numbers is 31. Find the numbers.
Solution:

Question 9.
Find a number such that when 5 is subtracted from 5 times the number, the result is 4 more than twice the number.
Solution:

Question 10.
The numerator of a fraction is 5 less than its denominator. If 3 is added to the numerator, and denominator both, the fraction becomes \(\frac { 2 }{ 3 }\). Find the original fraction.
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Publishers Concise Biology Class 7 ICSE Solutions Chapter 1 Plant And Animal Tissues

Selina Concise Biology Class 7 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 16 Pythagoras Theorem

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 16 Pythagoras Theorem

Pythagoras Theorem Exercise 16 – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Solution:

Question 2.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
Solution:

Question 3.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if:
PQ = 34 cm and QR = 33.6 cm.
Solution:

Question 4.
The sides of a certain triangle are given below. Find, which of them is right-triangle
(i) 16 cm, 20 cm and 12 cm
(ii) 6 m, 9 m and 13 m
Solution:

Question 5.
In the given figure, angle BAC = 90°, AC = 400 m and AB = 300 m. Find the length of BC.

Solution:

Question 6.
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD
Solution:

Question 7.
In triangle PQR, angle Q = 90°, find :
(i) PR, if PQ = 8 cm and QR = 6 cm
(ii) PQ, if PR = 34 cm and QR = 30 cm
Solution:

Question 8.
Show that the triangle ABC is a right-angled triangle; if:
AB = 9 cm, BC = 40 cm and AC = 41 cm
Solution:

Question 9.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

Solution:

Question 10.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

Solution:

Question 11.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

Solution:

Question 12.
A ladder, 6.5 m long, rests against a vertical wall. Ifthe foot of the ladcler is 2.5 m from the foot of the wall, find upto how much height does the ladder reach?
Solution:

Question 13.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Solution:

Question 14.
Use the information given in the figure to find the length AD.

Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 12 Algebraic Identities

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 12 Algebraic Identities

Algebraic Identities Exercise 12A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Use direct method to evaluate the following products :
(i) (x + 8)(x + 3)
(ii) (y + 5)(y – 3)
(iii) (a – 8)(a + 2)
(iv) (b – 3)(b – 5)
(v) (3x – 2y)(2x + y)
(vi) (5a + 16)(3a – 7)
(vii) (8 – b) (3 + b)
Solution:

Question 2.
Use direct method to evaluate :

Solution:

Question 3.
Evaluate :

Solution:

Question 4.
Use the product (a + b) (a – b) = a² – b² to evaluate:
(i) 21 × 19
(ii) 33 × 27
(iii) 103 × 97
(iv) 9.8 × 10.2
(v) 7.7 × 8.3
(vi) 4.6 × 5.4
Solution:

Question 5.
Evaluate :
(i) (6 – xy) (6 + xy)

Solution:

Algebraic Identities Exercise 12B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Expand :
(i) (2a + b)²
(ii) (a – 2b)²

Solution:

Question 2.
Find the square of :

Solution:

Question 3.
Evaluate:
Using expansion of (a + b)² or (a – b)²
(i) (208)²
(ii) (92)²
(iii)(415)²
(iv) (188)²
(v) (9.4)²
(vi) (20.7)²
Solution:

Question 4.
Expand :

Solution:

Question 5.
Find the cube of :

Solution:

Algebraic Identities Exercise 12C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
If a  +b = 5 and ab = 6; find a² + b²
Solution:

Question 2.
If a – b = 6 and ab = 16; find a² + b²
Solution:

Question 3.
If a² + b² = 29 and ab = 10 ; find :
(i) a + b
(ii) a – b
Solution:

Question 4.
If a² + b² = 10 and ab = 3; find :
(i) a – b
(ii) a + b
Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.
If a + b + c = 10 and a² + b² + c² = 38; find ab + bc + ca
Solution:

Question 10.
Find a² + b² + c² ; if a + b + c = 9 and ab + bc + ca = 24
Solution:

Question 11.
Find a + b + c; if a² + b² + c² = 83 and ab + bc + ca = 71
Solution:

Question 12.
If a + b = 6 and ab=8; find a³ + b³
Solution:

Question 13.
If a – b = 3 and ab = 10; find a³ – b³
Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.
The sum of the squares of two numbers is 13 and their product is 6. Find:
(i) the sum of the two numbers.
(ii) the difference between them.
Solution:

Algebraic Identities Exercise 12D – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Evaluate:

Solution:

Question 2.
Evaluate:

Solution:

Question 3.
Find the square of :

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.
If a² + b² = 41 and ab = 4, find :
(i) a – b
(ii) a + b
Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.
Expand :
(i) (3x – 4y + 5z)²
(ii) (2a – 5b – 4c)²
(iii) (5x + 3y)³
(iv) (6a – 7b)³
Solution:

Question 10.
If a + b + c = 9 and ab + bc + ca = 15, find: a² + b² + c².
Solution:

Question 11.
If a + b + c = 11 and a² + b² + c² = 81, find ab + bc + ca.
Solution:

Question 12.
If 3x – 4y = 5 and xy = 3, find : 27x³ – 64y³.
Solution:

Question 13.
If a + b = 8 and ab = 15, find : a³ + b³.
Solution:

Question 14.
If 3x + 2y = 9 and xy = 3, find : 27x³ + 8y³
Solution:

Question 15.
If 5x – 4y = 7 and xy = 8, find : 125x³ – 64y³
Solution:

Question 16.
The difference between two numbers is 5 and their products is 14. Find the difference between their cubes.
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 15 Triangles

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 15 Triangles

Triangles Exercise 15A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Stale, if the triangles are possible with the following angles :
(i) 20°, 70° and 90°
(ii) 40°, 130° and 20°
(iii) 60°, 60° and 50°
(iv) 125°, 40° and 15°
Solution:

Question 2.
If the angles of a triangle are equal, find its angles.
Solution:

Question 3.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
Solution:

Question 4.
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Solution:

Question 5.
Calculate the unknown marked angles in each figure :

Solution:

Question 6.
Find the value of each angle in the given figures:

Solution:

Question 7.
Find the unknown marked angles in the given figure:

Solution:

Question 8.
In the given figure, show that: ∠a = ∠b + ∠c

(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
Solution:

Question 9.
Calculate the angles of a triangle if they are in the ratio 4 : 5 : 6.
Solution:

Question 10.
One angle of a triangle is 60°. The, other two angles are in the ratio of 5 : 7. Find the two angles.
Solution:

Question 11.
One angle of a triangle is 61° and the other two angles are in the ratio 1\(\frac { 1 }{ 2 }\) : 1 \(\frac { 1 }{ 3 }\). Find these angles.
Solution:

Question 12.
Find the unknown marked angles in the given figures :

Solution:

Triangles Exercise 15B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Find the unknown angles in the given figures:

Solution:

Question 2.
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figures :

Solution:

Question 3.
The angle of vertex of an isosceles triangle is 100°. Find its base angles.
Solution:

Question 4.
One of the base angles of an isosceles triangle is 52°. Find its angle of vertex.
Solution:

Question 5.
In an isosceles triangle, each base angle is four times of its vertical angle. Find all the angles of the triangle.
Solution:

Question 6.
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
Solution:

Question 7.
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
Solution:

Question 8.
The vertical angle of an isosceles triangle is three times the sum of its base angles. Find each angle.
Solution:

Question 9.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1 : 4. Find each angle of the triangle.
Solution:

Question 10.
In the given figure, BI is the bisector of∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.

Solution:

Question 11.
In the given figure, express a in terms of b.

Solution:

Question 12.
(a) In Figure (i) BP bisects ∠ABC and AB = AC. Find x.
(b) Find x in Figure (ii) Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.

Solution:

Question 13.
In each figure, given below, ABCD is a square and ∆ BEC is an equilateral triangle.
Find, in each case : (i) ∠ABE(ii) ∠BAE

Solution:

Question 14.
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.

Solution:

Triangles Exercise 15C – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Construct a ∆ABC such that:
(i) AB = 6 cm, BC = 4 cm and CA = 5.5 cm
(ii) CB = 6.5 cm, CA = 4.2 cm and BA = 51 cm
(iii) BC = 4 cm, AC = 5 cm and AB = 3.5 cm
Solution:

Question 2.
Construct a A ABC such that:
(i) AB = 7 cm, BC = 5 cm and ∠ABC = 60°
(ii) BC = 6 cm, AC = 5.7 cm and ∠ACB = 75°
(iii) AB = 6.5 cm, AC = 5.8 cm and ∠A = 45°
Solution:

Question 3.
Construct a ∆ PQR such that :
(i) PQ = 6 cm, ∠Q = 60° and ∠P = 45°. Measure ∠R.
(ii) QR = 4.4 cm, ∠R = 30° and ∠Q = 75°. Measure PQ and PR.
(iii) PR = 5.8 cm, ∠P = 60° and ∠R = 45°.
Measure ∠Q and verify it by calculations
Solution:

Question 4.
Construct an isosceles A ABC such that:
(i) base BC = 4 cm and base angle = 30°
(ii) base AB = 6-2 cm and base angle = 45°
(iii) base AC = 5 cm and base angle = 75°.
Measure the other two sides of the triangle.
Solution:

Question 5.
Construct an isosceles ∆ABC such that:
(i) AB = AC = 6.5 cm and ∠A = 60°
(ii) One of the equal sides = 6 cm and vertex angle = 45°. Measure the base angles.
(iii) BC = AB = 5-8 cm and ZB = 30°. Measure ∠A and ∠C.
Solution:

Question 6.
Construct an equilateral A ABC such that:
(i) AB = 5 cm. Draw the perpendicular bisectors of BC and AC. Let P be the point of intersection of these two bisectors. Measure PA, PB and PC.
(ii) Each side is 6 cm.
Solution:

Question 7.
(i) Construct a ∆ ABC such that AB = 6 cm, BC = 4.5 cm and AC = 5.5 cm. Construct a circumcircle of this triangle.
(ii) Construct an isosceles ∆PQR such that PQ = PR = 6.5 cm and ∠PQR = 75°. Using ruler and compasses only construct a circumcircle to this triangle.
(iii) Construct an equilateral triangle ABC such that its one side = 5.5 cm.
Construct a circumcircle to this triangle.
Solution:

Question 8.
(i) Construct a ∆ABC such that AB = 6 cm, BC = 5.6 cm and CA = 6.5 cm. Inscribe a circle to this triangle and measure its radius.
(ii) Construct an isosceles ∆ MNP such that base MN = 5.8 cm, base angle MNP = 30°. Construct an incircle to this triangle and measure its radius.
(iii) Construct an equilateral ∆DEF whose one side is 5.5 cm. Construct an incircle to this triangle.
(iv) Construct a ∆ PQR such that PQ = 6 cm, ∠QPR = 45° and angle PQR = 60°. Locate its incentre and then draw its incircle.
Solution:

Selina Concise Mathematics Class 7 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 23 Probability

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 23 Probability

Probability Exercise 23 – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
A die is thrown, find the probability of getting:
(i) a prime number
(ii) a number greater than 4
(iii) a number not greater than 4.
Solution:

Question 2.
A coin is tossed. What is the probability of getting:
(i) a tail? (ii) ahead?
Solution:

Question 3.
A coin is tossed twice. Find the probability of getting:
(i) exactly one head (ii) exactly one tail
(iii) two tails (iv) two heads
Solution:

Question 4.
A letter is chosen from the word ‘PENCIL’ what is the probability that the letter chosen is a consonant?
Solution:

Question 5.
A bag contains a black ball, a red ball and a green ball, all the balls are identical in shape and size. A ball is drawn from the bag without looking into it. What is the probability that the ball drawn is:
(i) a red ball
(ii) not a red ball
(iii) a white ball.
Solution:

Question 6.
6. In a single throw of a die, find the probability of getting a number
(i) greater than 2
(ii) less than or equal to 2
(iii) not greater than 2.
Solution:

Question 7.
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size.
A ball is drawn from the bag without looking into it, find the probability that the ball drawn is:
(i) a black ball.
(ii) a red ball.
(iii) a white ball.
(iv) not a red ball.
(v) not a black ball.
Solution:

Question 8.
In a single throw of a die, find the probability that the number:
(i) will be an even number.
(ii) will be an odd number.
(iii) will not be an even number.
Solution:

Question 9.
In a single throw of a die, find the probability of getting :
(i) 8
(ii) a number greater than 8
(iii) a number less than 8
Solution:

Question 10.
Which of the following can not be the probability of an event?

Solution:

Question 11.
A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:
(i) a white ball,
(ii) a black ball
Solution:

Question 12.
Three identical coins are tossed together. What is the probability of obtaining:
all heads?
exactly two heads?
exactly one head?
no head?
Solution:

Question 13.
A book contains 92 pages. A page is chosen at random. What is the probability that the sum of the digits in the page number is 9?
Solution:

Question 14.
Two coins are tossed together. What is the probability of getting:
(i) at least one head
(ii) both heads or both tails.
Solution:

Question 15.
From 10 identical cards, numbered 1, 2, 3, …… , 10, one card is drawn at random. Find the probability that the number on the card drawn is a multiple of:
(i) 2 (ii) 3
(iii) 2 and 3 (iv) 2 or 3
Solution:

Question 16.
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is:
(i) 0
(ii) 12
(iii) less than 12
(iv) less than or equal to 12
Solution:

Question 17.
A die is thrown once. Find the probability of getting:
(i) a prime number
(ii) a number greater than 3
(iii) a number other than 3 and 5
(iv) a number less than 6
(v) a number greater than 6.
Solution:

Question 18.
Two coins are tossed together. Find the probability of getting:
(i) exactly one tail
(ii) at least one head
(iii) no head
(iv) at most one head
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 13 Factorisation

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 13 Factorisation

Factorisation Exercise 13A – Selina Concise Mathematics Class 8 ICSE Solutions

Factorise :
Question 1.
15x + 5
Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Factorisation Exercise 13B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Factorise : a² + ax + ab + bx
Solution:

Question 2.
Factorise : a² – ab – ca + bc
Solution:

Question 3.
Factorise : ab – 2b + a² – 2a
Solution:

Question 4.
Factorise : a³ – a² + a – 1
Solution:

Question 5.
Factorise : 2a – 4b – xa + 2bx
Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Factorisation Exercise 13C – Selina Concise Mathematics Class 8 ICSE Solutions

Note : a² – b² = (a + b) (a – b)
Question 1.
Factorise : 16 – 9x²
Solution:

Question 2.
Factorise : 1 – 100a²
Solution:

Question 3.
Factorise : 4x² – 81y²
Solution:

Question 4.

Solution:

Question 5.
Factorise : (a+2b)² – a²
Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.
Evaluate :

Solution:

Question 15.
Evaluate :
(0.7)² – (0.3)²
Solution:

Question 16.
Evaluate :
(4.5)² – (1.5)²
Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Factorisation Exercise 13D – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:
<

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21.

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.

Solution:

Question 25.

Solution:

Factorisation Exercise 13E – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
In each case find whether the trinomial is a perfect square or not:

Solution:

Question 2.
Factorise completely 2 – 8x².
Solution:

Question 3.
Factorise completely : 8x²y – 18y³
Solution:

Question 4.
Factorise completely : ax² – ay²
Solution:

Question 5.
Factorise completely : 25x³ – x
Solution:

Question 6.
Factorise completely : a⁴ – b⁴
Solution:

Question 7.
Factorise completely : 16x⁴ – 81y⁴
Solution:

Question 8.
Factorise completely : 625 – x⁴
Solution:

Question 9.
Factorise completely : x² – y² – 3x – 3y
Solution:

Question 10.
Factorise completely : x² – y² – 2x + 2y
Solution:

Question 11.
Factorise completely : 3x² + 15x – 72
Solution:

Question 12.
Factorise completely : 2a² – 8a – 64
Solution:

Question 13.
Factorise completely : 5b² + 45b + 90
Solution:

Question 14.
Factorise completely : 3x²y + 11xy + 6y
Solution:

Question 15.
Factorise completely : 5ap² + 11ap + 2a
Solution:

Question 16.
Factorise completely : a² + 2ab + b² – c²
Solution:

Question 17.
Factorise completely : x² + 6xy + 9y² + x + 3y
Solution:

Question 18.
Factorise completely : 4a² – 12ab + 9b² + 4a – 6b
Solution:

Question 19.
Factorise completely : 2a²b² – 98b⁴
Solution:

Question 20.
Factorise completely : a² – 16b² – 2a – 8b
Solution:

Factorisation Exercise 13F – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Factorise :

Solution:

Question 2.
Factorise :

Solution:

Question 3.
Factorise :

Solution:

Question 4.
Factorise :

Solution:

Question 5.
Factorise :

Solution:

Question 6.
Factorise :


Solution:

Question 7.
Factorise xy² – xz², Hence, find the value of:

Solution:

Question 8.
Factorise :

Solution:

Question 9.
Factorise a²b – b³ Using this result, find the value of 101² × 100 – 100³.
Solution:

Question 10.
Evaluate (using factors): 301² × 300 – 300³.
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 22 Data Handling

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 22 Data Handling

Data Handling Exercise 22A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Arrange the following data as an array (in ascending order):
(i) 7, 5, 15, 12, 10, 11, 16
(ii) 6.3, 5.9, 9.8, 12.3, 5.6, 4.7
Solution:

Question 2.
Arrange the following data as an array (descending order):
(i) 0 2, 0, 3, 4, 1, 2, 3, 5
(ii) 9.1, 3.7, 5.6, 8.3, 11.5, 10.6
Solution:

Question 3.
Construct a frequency table for the following data:
(i) 6, 7, 5, 6, 8, 9, 5, 5, 6, 7, 8, 9, 8, 10, 10, 9, 8, 10, 5, 7, 6, 8.
(ii) 3, 2, 1, 5, 4, 3, 2, 5, 5, 4, 2, 2, 2, 1, 4, 1, 5, 4.
Solution:

Question 4.
Following are the marks obtained by 30 students in an examinations.

Taking class intervals 0-10, 10-20, ……… 40-50 ; construct a frequency table.
Solution:

Question 5.
Construct a frequency distribution table for the following data ; taking class-intervals 4-6, 6-8, ……… 14-16.

Solution:

Question 6.
Fill in the blanks:
(i) Lower class limit of 15-18 is ………
(ii) Upper class limit of 24-30 is ……..
(iii) Upper limit of 5-12.5 is ………
(iv) If the upper and the lower limits of a class interval are 16 and 10 ; the class-interval is ……..
(v) If the lower and the upper limits of a class interval are 7.5 and 12.5 ; the class interval is ……..
Solution:

Data Handling Exercise 22B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Hundred students from a certain locality use different modes of travelling to school as given below. Draw a bar graph.

Solution:

Question 2.
Mr. Mirza’s monthly income is Rs. 7,200. He spends Rs. 1,800 on rent, Rs. 2,700 on food, Rs. 900 on education of his children ; Rs. 1,200 on Other things and saves the rest.
Draw a pie-chart to represent it.
Solution:

Question 3.
The percentage of marks obtained, in different subjects by Ashok Sharma (in an examination) are given below. Draw a bar graph to represent it.

Solution:

Question 4.
The following table shows the market position of different brand of tea-leaves.

Draw it-pie-chart to represent the above information.
Solution:

Question 5.
Students of a small school use different modes of travel to school as shown below:

Draw a suitable bar graph.
Solution:

Question 6.
For the following table, draw a bar-graph

Solution:

Question 7.
Manoj appeared for ICSE examination 2018 and secured percentage of marks as shown in the following table:

Represent the above data by drawing a suitable bar graph.
Solution:

Question 8.
For the data given above in question number 7, draw a suitable pie-graph.
Solution:

Question 9.
Mr. Kapoor compares the prices (in Rs.) of different items at two different shops A and B. Examine the following table carefully and represent the data by a double bar graph.

Solution:

Question 10.
The following tables shows the mode of transport used by boys and girls for going to the same school.

Draw a double bar graph representing the above data.
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 21 Surface Area, Volume and Capacity (Cuboid, Cube and Cylinder)

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 21 Surface Area, Volume and Capacity (Cuboid, Cube and Cylinder)

Surface Area, Volume and Capacity Exercise 21A – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
Find the volume and the total surface area of a cuboid, whose :
(i) length = 15 cm, breadth = 10 cm and height = 8 cm.
(ii) l = 3.5 m, b = 2.6 m and h = 90 cm,
Solution:

Question 2.
(i) The volume of a cuboid is 3456 cm³. If its length = 24 cm and breadth = 18 cm ; find its height.
(ii) The volume of a cuboid is 7.68 m³. If its length = 3.2 m and height = 1.0 m; find its breadth.
(iii) The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m³; find its length.
Solution:

Question 3.
The length, breadth and height of a cuboid are in the ratio 5 : 3 : 2. If its volume is 240 cm³; find its dimensions. (Dimensions means : its length, breadth and height). Also find the total surface area of the cuboid.
Solution:

Question 4.
The length, breadth and height of a cuboid are in the ratio 6 : 5 : 3. If its total surface area is 504 cm2; find its dimensions. Also, find the volume of the cuboid.
Solution:

Question 5.
Find the volume and total surface area of a cube whose each edge is :
(i) 8 cm
(ii) 2 m 40 cm.
Solution:

Question 6.
Find the length of each edge of a cube, if its volume is :
(i) 216 cm³
(ii) 1.728 m³
Solution:

Question 7.
The total surface area of a cube is 216 cm2. Find its volume.
Solution:

Question 8.
A solid cuboid of metal has dimensions 24 cm, 18 cm and 4 cm. Find its volume.
Solution:

Question 9.
A wall 9 m long, 6 m high and 20 cm thick, is to be constructed using bricks of dimensions 30 cm, 15 cm and 10 cm. How many bricks will be required.
Solution:

Question 10.
A solid cube of edge 14 cm is melted down and recasted into smaller and equal cubes each of edge 2 cm; find the number of smaller cubes obtained.
Solution:

Question 11.
A closed box is cuboid in shape with length = 40 cm, breadth = 30 cm and height = 50 cm. It is made of thin metal sheet. Find the cost of metal sheet required to make 20 such boxes, if 1 m² of metal sheet costs Rs. 45.
Solution:

Question 12.
Four cubes, each of edge 9 cm, are joined as shown below :

Write the dimensions of the resulting cuboid obtained. Also, find the total surface area and the volume of the resulting cuboid.
Solution:

Surface Area, Volume and Capacity Exercise 21B – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
How many persons can be accommodated in a big-hall of dimensions 40 m, 25 m and 15 m ; assuming that each person requires 5 m³ of air?
Solution:

Question 2.
The dimension of a class-room are; length = 15 m, breadth = 12 m and height = 7.5 m. Find, how many children can be accommodated in this class-room ; assuming 3.6 m³ of air is needed for each child.
Solution:

Question 3.
The length, breadth and height of a room are 6 m, 5.4 m and 4 m respectively. Find the area of :
(i) its four-walls
(ii) its roof.
Solution:

Question 4.
A room 5 m long, 4.5 m wide and 3.6 m high has one door 1.5 m by 2.4 m and two windows, each 1 m by 0.75 m. Find :
(i) the area of its walls, excluding door and windows ;
(ii) the cost of distempering its walls at the rate of Rs.4.50 per m².
(iii) the cost of painting its roof at the rate of Rs.9 per m².
Solution:

Question 5.
The dining-hall of a hotel is 75 m long ; 60 m broad and 16 m high. It has five – doors 4 m by 3 m each and four windows 3 m by 1.6 m each. Find the cost of :
(i) papering its walls at the rate of Rs.12 per m²;
(ii) carpetting its floor at the rate of Rs.25 per m².
Solution:

Question 6.
Find the volume of wood required to make a closed box of external dimensions 80 cm, 75 cm and 60 cm, the thickness of walls of the box being 2 cm throughout.
Solution:

Question 7.
A closed box measures 66 cm, 36 cm and 21 cm from outside. If its walls are made of metal-sheet, 0.5 cm thick ; find :
(i) the capacity of the box ;
(ii) volume of metal-sheet and
(iii) weight of the box, if 1 cm³ of metal weights 3.6 gm.
Solution:

Question 8.
The internal length, breadth and height of a closed box are 1 m, 80 cm and 25 cm. respectively. If its sides are made of 2.5 cm thick wood ; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
Solution:

Question 9.
Find the area of metal-sheet required to make an open tank of length = 10 m, breadth = 7.5 m and depth = 3.8 m.
Solution:

Question 10.
A tank 30 m long, 24 m wide and 4.5 m deep is to be made. It is open from the top. Find the cost of iron-sheet required, at the rate of ₹ 65 per m², to make the tank.
Solution:

Surface Area, Volume and Capacity Exercise 21C – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
The edges of three solid cubes are 6 cm, 8 cm and 10 cm. These cubes are melted and recast into a single cube. Find the edge of the resulting cube.
Solution:

Question 2.
Three solid cubes of edges 6 cm, 10 cm and x cm are melted to form a single cube of edge 12 cm, find the value of x.
Solution:

Question 3.
The length of the diagonals of a cube is 8√3 cm.
Find its:
(i) edge
(ii) total surface area
(iii) Volume
Solution:

Question 4.
A cube of edge 6 cm and a cuboid with dimensions 4 cm x x cm x 15 cm are equal in volume. Find:
(i) the value of x.
(ii) total surface area of the cuboid.
(iii) total surface area of the cube.
(iv) which of these two has greater surface and by how much?
Solution:

Question 5.
The capacity of a rectangular tank is 5.2 m³ and the area of its base is 2.6 x 104 cm²; find its height (depth).
Solution:

Question 6.
The height of a rectangular solid is 5 times its width and its length is 8 times its height. If the volume of the wall is 102.4 cm³, find its length.
Solution:

Question 7.
The ratio between the lengths of the edges of two cubes are in the ratio 3 : 2. Find the ratio between their:
(i) total surface area
(ii) volume.
Solution:

Question 8.
The length, breadth and height of a cuboid (rectangular solid) are 4 : 3 : 2.
(i) If its surface are is 2548 cm², find its volume.
(ii) If its volume is 3000 m³, find its surface area.
Solution:

Surface Area, Volume and Capacity Exercise 21D – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
The height of a circular cylinder is 20 cm and the diameter of its base is 14 cm. Find:
(i) the volume
(ii) the total surface area.
Solution:

Question 2.
Find the curved surface area and the total surface area of a right circular cylinder whose height is 15 cm and the diameter of the cross-section is 14 cm.
Solution:

Question 3.
Find the height of the cylinder whose radius is 7 cm and the total surface area is 1100 cm².
Solution:

Question 4.
The curved surface area of a cylinder of height 14 cm is 88 cm². Find the diameter of the base of the cylinder.
Solution:

Question 5.
The ratio between the curved surface area and the total surface area of a cylinder is 1 : 2. Find the ratio between the height and the radius of the cylinder.
Solution:

Question 6.
Find the capacity of a cylindrical container with internal diameter 28 cm and height 20 cm.
Solution:

Question 7.
The total surface area of a cylinder is 6512 cm² and the circumference of its bases is 88 cm. Find:
(i) its radius
(ii) its volume
Solution:

Question 8.
The sum of the radius and the height of a cylinder is 37 cm and the total surface area of the cylinder is 1628 cm². Find the height and the volume of the cylinder.
Solution:

Question 9.
A cylindrical pillar has radius 21 cm and height 4 m. Find :
(i) the curved surface area of the pillar
(ii) cost of polishing 36 such cylindrical pillars at the rate of ₹ 12 per m².
Solution:

Question 10.
If radii of two cylinders are in the ratio 4 : 3 and their heights are in the ratio 5 : 6, find the ratio of their curved surfaces.
Solution:

Surface Area, Volume and Capacity Exercise 21E – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
A cuboid is 8 m long, 12 m broad and 3.5 high, Find its
(i) total surface area
(ii) lateral surface area
Solution:

Question 2.
How many bricks will be required for constructing a wall which is 16 m long, 3 m high and 22.5 cm thick, if each brick measures 25 cm x 11.25 cm x 6 cm?
Solution:

Question 3.
The length, breadth and height of cuboid are in the ratio 6 : 5 : 3. If its total surface area is 504 cm², find its volume.
Solution:

Question 4.
The external dimensions of an open wooden box are 65 cm, 34 cm and 25 cm. If the box is made up of wood 2 cm thick, find the capacity of the box and the volume of wood used to make it.
Solution:

Question 5.
The curved surface area and the volume of a toy, cylindrical in shape, are 132 cm² and 462 cm³ respectively. Find, its diameter and its length.
Solution:

Question 6.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m² is ₹ 15,000, find the height of the hall.
Solution:

Question 7.
The length of a hall is double its breadth. Its height is 3 m. The area of its four walls (including doors and windows) is 108 m², find its volume.
Solution:

Question 8.
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
Solution:

Question 9.
The diameter of a garden roller is 1.4 m and it 2 m long. Find the maximum area covered by it 50 revolutions?
Solution:

Question 10.
In a building, there are 24 cylindrical pillars. For each pillar, radius is 28 m and height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m².
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions