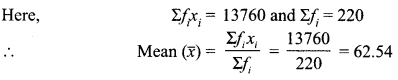CBSE Sample Papers for Class 10 Maths Basic Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 3 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.

Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.

Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.

Part – A
Section-I

Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.

Question 1.
Express 225 as the product of prime numbers.
Solution :

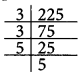
225 = 3 x 3 x 5 x 5
= 3² x 5²

Question 2.
The sum and product of the zeroes of a quadratic polynomial are 3 and -10 respectively. The quadratic polynomial is Solution :
Let the zeroes of a quadratic polynomial be a and p.
Then  α + β = 3 and αβ =-10
So, required polynomial
p(x) = x² – (a + p)x + ap = x² – 3x – 10

Question 3.
HCF of 144 and 198 is 18, find the LCM of 144 and 198.
OR
Explain why 3 x 5 x 7 + 7 is a composite number.
Solution :
Let a = 144 and b = 198
Then a x b = HCF x LCM
⇒ 144 x 198= 18 x LCM

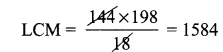
OR
3 x 5 x 7 + 7= (15 + 1) x 7
= 16 x 7 = 112 = 2 x 2 x 2 x 2 x 7
= Product of prime factors
Hence, it is a composite number.

Question 4.
If the equations kx – 2y = 3 and 3x + y = 5 represent two intersecting lines at unique point, then find the value of k
Solution :
Lines kx -2y = 3 and 3x + y = 5 intersect at unique point.
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \Rightarrow \frac{k}{3} \neq \frac{-2}{1} \Rightarrow k \neq-6\)
∴ k has any real value except 6.

Question 5.
The decimal expansion of the rational number of \(\frac{43}{2^{4} 5^{3}}\) will terminate after how many places
Solution :
Here we have a rational number of the form \(\frac{p}{q}\) and the prime factorisation of q is of the form 2ⁿ5^m,
Now, \(\frac{43}{2^{4} 5^{3}}=\frac{43 \times 5}{2^{4} 5^{4}}=\frac{215}{10^{4}}=0.0215\)
where n, m are non-negative integers, so decimal expansion of given rational number terminates.

Question 6.
The radius of a circle is 5 cm. Find the radius of the circle whose area is 49 times the area of the given circle.
OR
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 6k cm.
Solution :
Area of the given circle = πr² = 25π sq. cm.
Area of other circle = 49 x 25π sq. cm.
Let radius of this circle be R.
Then  πR² = 49 x 25π
⇒ R² = 7² × 5² = R = 7 x 5 = 35 cm.
OR
Here l = 6π, r = 6 cm, θ = ?
∵ \(l=\frac{\pi r \theta}{180^{\circ}} \Rightarrow 6 \pi=\frac{\pi \times 6 \times \theta}{180^{\circ}}\)
∴ θ = 180°

Question 7.
The angle of elevation of the top of a tower from a point 15 metres away from the base is 30°. Find the height of the tower
OR
Find the angle of depression from the top of 12 m tall tower of an object lying at a point 12 m away from the base of the tower.
Solution :
Let AB be the tower and C the point 15 m away from the base of the tower.

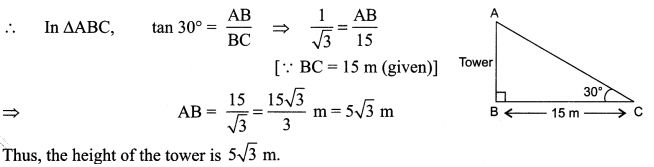
OR
Let AB be the tower of 12 m height and B its base. Let C be a point 12 m away from base B of tower AB where an object is situated.


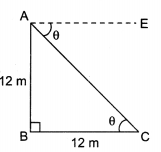
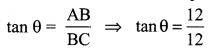
tan θ = 1
tan θ = tan 45° ⇒ θ = 45°
Thus, angle of depression = ∠EAC = ∠ACB = 45°

Question 8.
The areas of two circles are in the ratio 9 : 4, then what is the ratio of their circumferences?
Solution :

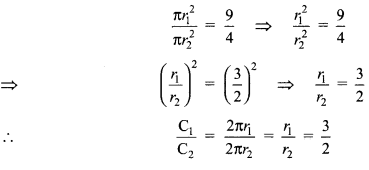
Question 9.
The angle of elevation of the top of a tower from a point on the ground is 30°. If the height of the tower is 20 m, find the distance of the point from the foot of the tower.
Solution :

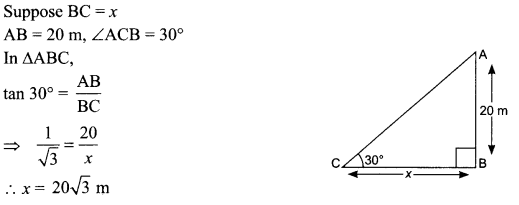
Question 10.
A road which is 7 m wide surrounds a circular park whose circumference is 88 m. Find the radius of the park.
Solution :

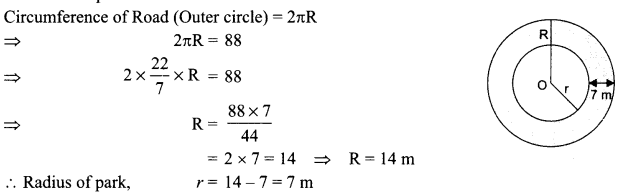
Question 11.
The median and mode respectively of a frequency distribution are 26 and 29. Then find its mean
Solution :
Median = 26
and Mode = 29
We know that 3 Median = Mode + 2 Mean
⇒ 3 x 26 = 29 + 2 Mean
⇒ 2 Mean = 78 – 29 = 49
Mean = 24.5

Question 12.
To divide line segment AB in the ratio m : n, we draw a ray AX so that ∠BAX is an acute angle and then mark points on ray AX at equal distance. What is the minimum number of these points on AX?
Solution :
m + n.

Question 13.
Find the value of k for which the given system has unique solution. 2x + 3y – 5 = 0, kx – 6y – 8 = 0
OR
If the pair of equations x sin 9 + y cos 0 = 1 and x + y = a/2 has infinitely many solutions, then what is the value of 0?
Solution :
For unique solution:

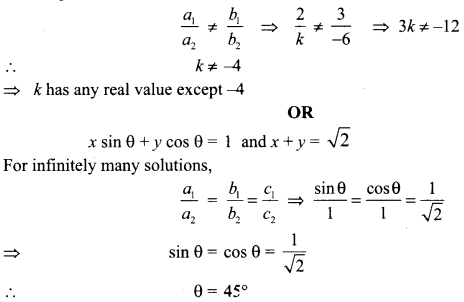
Question 14.
Find the probability that a number selected at random from the numbers 1,2,3, of 4
OR
If a pair of dice is thrown once, then what is the probability of getting a sum of 8?
Solution :
Number of outcomes = 15 (i.e., 1, 2,…, 15)
Number of favourable outcomes = 3 (i.e., 4, 8, 12)
P(multiples of 4) \(\frac{3}{15}=\frac{1}{5}\)
OR
Number of outcomes = 36
Favourable outcomes = (2, 6), (3, 5), (4, 4), (5, 3) and (6, 2)
Number of favourable outcomes = 5
P(getting a sum of 8) \(=\frac{5}{36}\)

Question 15.
Find the angle of depression from the top of 12 m high tower of an object lying at a point 12 m away from the base of the tower.
Solution :
Let AB be the tower and C the point 12 m away from the base of the tower.

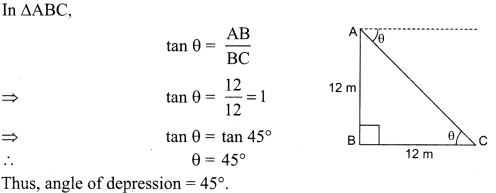
Question 16.
Two different dice are thrown together, find the probability that the sum of the numbers appeared is less than 5. 1
Solution :
Number of outcomes = 36
Favourable outcomes = (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (3, 1)
Number of favourable outcomes = 6
\(\mathrm{P}(\mathrm{sum}<5)=\frac{6}{36}=\frac{1}{6}\)

Section – II

Case study-based questions are compulsory. Attempt any 4 sub-parts from each question. Each sub-part carries 1 mark.
Case Study Based-I

Question 17.
Students of class X^th standard managed to visit Qutub Minar on an educational trip. Their teacher narrated the facts of Qutub Minar.

The teacher said that the monument is made of red sandstone and marble. with a 73-meters tall tapering tower of five stories with 14.3 metres base diametre. The students also saw iron pillar of Ashoka.

(i) What is the angle of elevation if they were standing at a distance of 73 metres away from the minar?
(a) 30°
(b) 45°
(c) 60°
(d) 0°

(ii) They want to see the tower at an angle of 60°. So, they want to know the distance where they should stand and hence find the distance.
(a) 30 m
(b) 35 m
(c) 42.14 m
(d) 45 m

(iii) Considering that the iron pillar is 3.5 metres tall and a radius of 14 cm.  What is the volume of cylindrical portion of the pillar?
(a) 205600 cu. cm
(b) 15560 cu.cm
(c) 244200 cu. cm
(d) 215600 cu.cm

(iv) Write the formula to find the curve surface of the cylindrical portion of the pillar.
(a) 2πrh
(b) πrh
(c) πr²h
(d) 2πr(r + h)

(v) What is the curved surface area of the pillar if it has its radius 14 cm and height 3.5 m?
(a) 20800 sq. cm
(b) 24600 sq. cm
(c) 35600 sq. cm
(d) 30800 sq. cm
Solution :

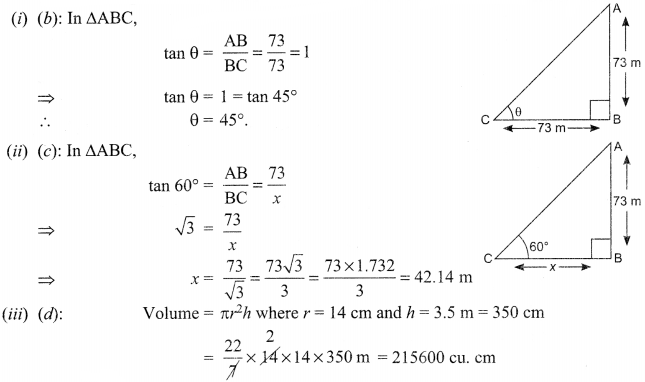
(iv) (a): Curved surface area of a cylinder = 2itrh
(y) (d): Curved surface area = 2πrh
Here r = 14cm and h = 3.5m = 3.5 x 100cm 350 cm

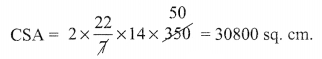
Case Study Based-2

Question 18.
To conduct sports day activities, in your rectangular-shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in figure. Niharika runs \(\frac{1}{4} \mathrm{th}\) the distance AD on the 2nd line and posts a green flag. Preet runs \(\frac{1}{5} th \) the distance AD on the eighth line and posts a red flag. Rashmi is in between these two girls with blue flag.

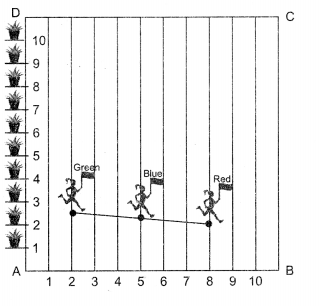
(i) Coordinates of Niharika are ……………
(a) (2,25)
(b) (25,2)
(c) (-2,25)
(d) (-25,2)

(ii) Coordinates of Preet are …………..
(a) (20, 8)
(b) (8, 20)
(c) (-20, 8)
(d) (-8, 20)

(iii) What is the distance between two flags?
(a) \(\sqrt{68}\)
(b)  \(\sqrt{71}\)
(c)  \(\sqrt{61}\)
(d) \(\sqrt{52}\)

(iv) Position of Rashmi’s flag is …………..
(a) (2,22.5)
(b) (22.5,2)
(c) (-2,22.5)
(d) (-22.5,2)

(v) If each flower pot costs ₹ 50. How much they have to pay for 100 pots?
(a) ₹  2000
(b) ₹  5000
(c) ₹ 3000
(d) ₹ 6000
Solution :
(i)  (a):(2,25)
Niharika runs \(\frac{1}{4} \text { th }\) the distance AD on 2nd line = \(\frac{1}{4} \text { th }\) x 100 = 25 4
So, coordinates of Niharika are (2, 25).

(ii) (b): (8, 20)
Preet runs \(\frac{1}{5} \text { th }\)distance AD on 8th line = \(\frac{1}{5} \text { th }\) x 100 = 20.
So Preet’s coordinate = (8,20).

(iii) (c):√61
Distance between two flags

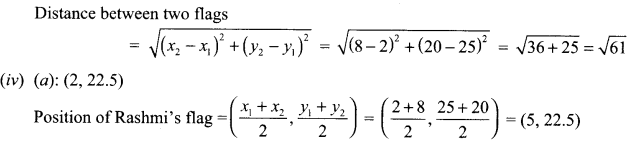
(v) (b): ₹ 5000.
Cost of one pot = ₹ 50
Cost of 100 pots = 100 x ₹ 50 = ₹ 5000

Case Study Based-3

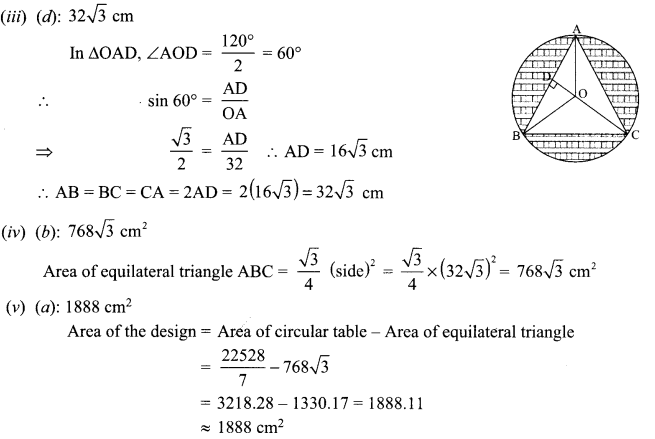
Question 19.
A student of class X standard finds in a circular table cover with radius 32 cm, a design which is formed leaving an equilateral triangle ABC in the middle as shown in the figure. Some questions arises in his mind which he shares with you. Help him to solve these questions.

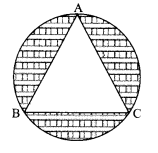
(i) What is the area of the circular table?
(a) \(\frac{22528}{7} \mathrm{~cm}^{2}\)
(b) \(\frac{20528}{7} \mathrm{~cm}^{2}\)
(c) \(\frac{22028}{7} \mathrm{~cm}^{2}\)
(d) \(\frac{28022}{7} \mathrm{~cm}^{2}\)

(ii) What is the measure of angle subtended by each side of the equilateral triangle at the centre of the circle?
(a) 30°
(b) 60°
(c) 120°
(d) 90°

(iii) Each side of the equilateral triangle is:
(a) \(64 \sqrt{3} \mathrm{~cm}\)
(b) \(8 \sqrt{3} \mathrm{~cm}\)
(c) \(16 \sqrt{3} \mathrm{~cm}\)
(d) \(32 \sqrt{3} \mathrm{~cm}\)

(iv) What is the area of equilateral triangle?
(a) \(700 \sqrt{3} \mathrm{~cm}^{2}\)
(b) \(768 \sqrt{3} \mathrm{~cm}^{2}\)
(c) \(678 \sqrt{3} \mathrm{~cm}^{2}\)
(d) \(876 \sqrt{3} \mathrm{~cm}^{2}\)

(v) What is the area of the design?
(a) 1888 cm²
(b) 1688 cm²
(c) 1988 cm²
(d) 1588 cm²
Solution :

Case Study Based-4

Question 20.
A child was playing with a rope. He laid the rope on two straight lines which were perpendicular to each other. He marked the horizontal line from -3 to 3 and vertical line from -2 to 2. The rope forms some mathematical shape which can be answered below:

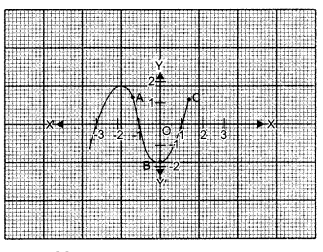
(i) What is the name of the shape from A, B to C?
(a) parabola
(b) linear
(c) elliptical
(d) spiral

(ii) How many zeroes are there for the polynomical (shape of the rope)?
(a) 3
(b) 1
(c) 2
(d) 4

(iii) The zeroes of the polynomial are
(a) 3,-1,2
(b) -3, -1,1
(c) 3, 1,-2
(d) -3, 2, -2

(iv) What will be the expression of the polynomial?
(a) x³ + 3x¹ – x – 3
(b) x² – 3x² + x + 3
(c) x³ + 3x² + x + 3
(d) x³ + 3x² + x – 3

(v) What is the degree of the polynomial so formed?
(a) 1
(b) 2
(c) 3
(d) 0
Solution :
(i) (a): parabola
(ii) (a) : The graph of the polynomial intersects the x-axis at three points.
So, the number of zeroes of the polynomial is 3.
(iii)
(b): -3,-1, 1
(a): x³ + 3x² -x- 3
(c): 3

Section-III
Part-B

All questions are compulsory. In case of internal choices, attempt anyone.

Question 21.
If the point C(k, 4) divides the line segment joining two points A(2, 6) and B(5, 1) in ratio 2:3, what is the value of k
OR
What is the coordinates of the mid-point of the line segment joining (4, 3) and (-2, -1)?
Solution :
C(k, 4) divides the line segment joining two points A(2, 6) and B(5, 1) in ratio 2:3

Let the points (4, 3) and (-2, -1) be denoted by A and B respectively.

Let M be the mid-point of AB. Coordinates of M are \(\left(\frac{4+(-2)}{2}, \frac{3+(-1)}{2}\right), \text { i.e. }(1,1)\)
Thus, the coordinates of the mid-point of the line segment joining (4, 3) and (-2, -1) are (1,1).

Question 22.
In an obtuse AABC (ZB is obtuse), AD is perpendicular to CB produced. Then prove that AC² = AB² + BC² + 2BC x BD.
Solution :

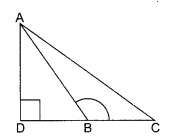
Given: A AABC in which ZB is obtuse and AD ⊥ BC.
To prove: AC² = AB² + BC² + 2BC x BD
Proof: In Δ ADC,
AC² = AD² + DC² [Pythagoras Theorem]
AC² = AD² + (DB + BC)²
AC² = AD² + DB² + BC² + 2DB x BC
AC² = AB² + BC² + 2DB x BC   [AD² + DB² = AB²]

Question 23.
In the given figure, a circle touches all the four sides of a quadrilateral ABCD in which AB = 6 cm, BC = 7 cm and CD = 4 cm. Find AD.

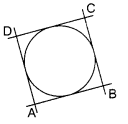
Solution :

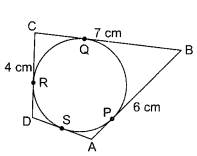
Given: Circle touches all the four sides of a quadrilateral ABCD.
Also , AB = 6 cm, BC = 7 cm and CD = 4 cm
Here AP = AS [Tangents from same external point]
Let AP = AS = x
Similarly BP = BQ, CQ = CR, RD = DS
Since AP = x
⇒ BP= AB – AP = 6-x
Now, BP = BQ = 6- x
CQ = BC – BQ = 7 – (6 – x) = 1 +x
Now CQ = CR = 1 +x
RD = CD – CR = 4- (1+x) = 3- x
Now RD = DS = 3 – x = SD
AD = AS + SD
= x + 3 – x = 3
AD = 3 cm

Question 24.
Draw a circle of radius 4 cm. From a point 7 cm away from the centre of circle. Construct a pair of tangents to the circle.
Solution :

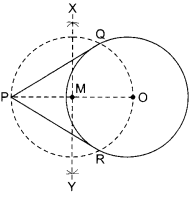
Steps of construction:
1. Taking radius of 4 cm, draw a circle with centre O.
2. Draw a line segment OP = 7 cm.
3. Draw XY, the perpendicular bisector of OP. Let it intersects OP at M.
4. With M as centre and radius equal to MO or MP, draw a circle. Let it intersects the given circle at points Q and R.
5. Join PQ and PR.

Question 25.
Prove that prove that \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sec \theta-\tan \theta\)
OR
Prove that \(\frac{\tan ^{2} \theta}{1+\tan ^{2} \theta}+\frac{\cot ^{2} \theta}{1+\cot ^{2} \theta}=1\)
Sol.

Question 26.
If 4 times the 4th term of an AP is equal to 18 times the 18th term, then find the 22nd term.
Solution :
Let a be the first term and d be the common difference of the AP.
Then its, 4th term = a + 3d
and its 18th term = a + 17d
We have
4(a + 3d) = 18(a+ 17d)
⇒ 4 a+ 12 d= 18a + 306d
⇒ 18a- 4a = 12d – 306d
⇒  14a = -294d
⇒ 14a + 294d= 0
⇒ 14(a + 21d) = 0
⇒ a + 21d= 0
⇒ a + (22 – 1)d = 0
So, 22nd term of AP = 0

Section-IV

Question 27.
Given that √3 is an irrational number, show that (5 + 2√3) is an irrational number.
Solution :
Suppose 5 + 2√3 is a rational number.

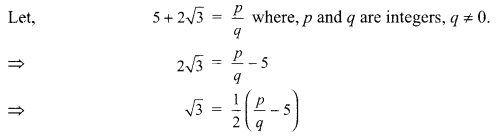
Here \(\frac{1}{2}\left(\frac{p}{q}-5\right)\) is rational number but √3 is an irrational number (given). This contradicts our assumption.
So, 5 + 2√3is an irrational number.

Question 28.
A right triangle ABC, right angled at A, is circumscribing a circle. If AB = 6 cm and BC = 10 cm, find the radius of the circle.
Solution :

Question 29.
Solve graphically: 2x + 3y = 2, x – 2y = 8
Solution :
We have
1x + 3y = 2
⇒ 3y= 2 – 2x
⇒ \(y=\frac{2-2 x}{3}\)

Tables of values

X	1	-2	4
y	0	2	-2

Plotting the value of above table and joining them by a straight line, we get a graph of 2x + 3y = 2.
Also, x – 2y = 8 ⇒ 2y = x – 8 ⇒ \(y=\frac{x-8}{2}\)

Table of values

X	0	2	4
y	-4	-3	-2

Plotting the values of above tables and joining them by a straight line, we get a graph of x – 2y = 8.

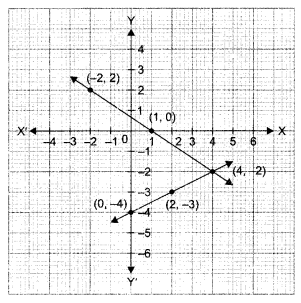
The two graph lines intersect at (4, -2)
x = 4 and y= -2 are the solutions of the given system of equations.

Question 30.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball at random from the bag is three times that of a red ball, find the number of blue balls in the bag.
OR
Find the probability that 5 Sundays occur in the month of November of a randomly selected year.
Solution :
Let the number of blue balls in the bag = x.

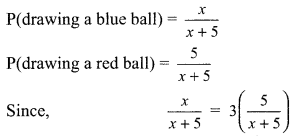
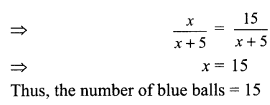
OR
We know that November has 30 days, which means 4 weeks and 2 days.
Now, 4 weeks will contain 4 Sundays.
The remaining 2 days may be (Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday) and (Saturday, Sunday).
Total number of possible outcomes = 7 Number of favourable outcomes = 2
∴ P(5 Sundays) = \(\frac{2}{7}\)

Question 31.
The rainwater from a roof 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m.
If the vessel is just full, find the rainfall in cm.
Solution :
Let L be the length and B the breadth of the roof.
Then, L = 22 m and B = 20 m. Let the rainfall in metres be x.
Then, the volume of rainwater drained from the roof into the cylindrical vessel
= LB x = 22 x 20 x x m³  ………… (i)
Let, r be the radius and h the height of the cylindrical vessel.
Then,
r= \(\frac{2}{2}m \)= 1 m and h = 3.5 m
The volume of the cylindrical vessel

Question 32.
Prove that

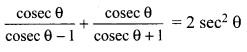
Solution :

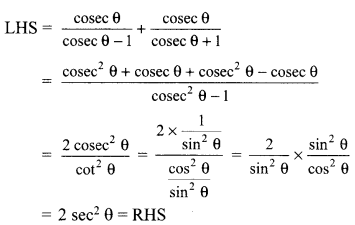
Question 33.
The difference of two natural numbers is 5 and the difference of their reciprocals is \(\frac{1}{10}\). Find the numbers.
OR
Find two consecutive odd natural numbers the sum of whose squares is 394.
Solution :
Let the smaller natural number be x.
Then greater natural number = x + 5

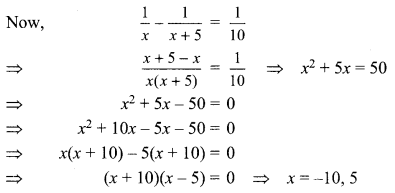
Natural number cannot be negative.
So, x = 5 So, smaller number = 5 and
greater number = 10
OR
Let first odd natural number be (2x -1) then other consecutive odd natural number be (2x+ 1)

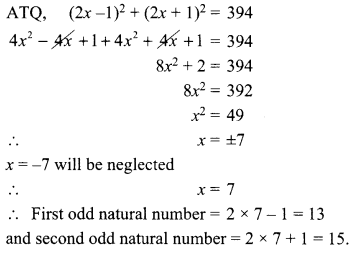
Section-V

Question 34.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
OR
In the given figure, ABC is a triangle in which AB = AC, D and E are points on the sides AB and AC respectively, such that AD = AE. Show that the points B, C, E and D are concylic.

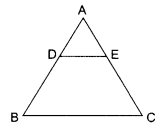
Solution :
Let AB be the lamp-post and CD be the girl after walking for 4 seconds away from the lamp-post. DE is the shadow of the girl.
Let DE = x cm.
BD = Distance covered by girl in 4 seconds = 1.2 x 4 = 4.8 m

Question 35.
Find the zeroes of the quadratic polynomial x² + lx + 10, and verify the relationship between the zeroes and the coefficients.
Solution :
We have,
p(x) = x² + 1x + 10
⇒ p(x) = x² + 5x + 2x + 10
⇒ x(x + 5) + 2(x + 5)
⇒ (x + 5) (x + 2)

Question 36.
Find the mean of the following data:

Classes	0 – 20	20 – 40	40 – 60	60 – 80	80 – 100	100­ – 120
Frequency	20	35	52	44	38	31

Solution :

Class interval	Frequency (fi)	Class Mark (xi)	fixi
0-20	20	10	200
20-40	35	30	1050
40-60	52	50	2600
60-80	44	70	3080
80-100	38	90	3420
100-120	31	110	3410
Total	∑ fi = 220		∑fixi – 13760