CBSE Sample Papers for Class 11 Physics Term 2 Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 11 Physics with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Physics Standard Term 2 Set 2 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks. :
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the choices in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

Section – A (2 Marks Each)

Question 1.
Derive the equation of continuity.
Answer:
Equation of continuity. Consider a non-viscous liquid in stream line flow through a tube AB of varying cross-section.
Let a₁ a₂ = area of cross-sections of the tube at A and B respectively,

υ₁ υ₂ = velocities of flow of liquid at A and B respectively.
ρ₁, ρ₂ = densities of liquid at A and B respectively.
∴ Volume of liquid entering per second at A = a₁υ₁
Mass of liquid entering per second at A = a₁υ₁ρ₁
Similarly, mass of liquid leaving per second at B = a₂υ₂ρ₂
If there is no loss of liquid in the tube and the flow is steady, then
Mass of liquid entering per second at A = Mass of liquid leaving per second at B
or a₁υ₁ρ₁ = a₁υ₁ρ₁ ………………… (1)
If the liquid is incompressible,
then ρ₁ = ρ₂
From (1) = a₁υ₁ = a₂υ₂
or aυ = (constant) ……………. (2)
This is known as equation of continuity.

Question 2.
Why the does the temperature of a gas decrease, when it is allowed to expand adiabatically ?
OR
State second law of thermodynamics.
Answer:
For an adiabatic change, the first law of thermodynamics may be expressed as
dU + PdV = 0
or PdV = – dU ………………. (i)
During expansion, dV is + υe. Therefore the equation (i) will hold, if dU is – υe, i.e., tempera-ture decreases.
OR
Kelvin’s statement: No process is possible whose sole result is the absorption of heat from a reservoir and complete conversion of the heat into work .

Clausius statement : It is not possible to transfer heat from a body at lower temperature to another at higher temperature without the help of some external energy.

Question 3.
What is beam ? What is its use ? Give an expression for the depression of a beam.
Answer:
Beam is ordinarily a bar supported at its ends.
It is used in the construction of a roof or a bridge.
δ = \(\frac{W l^{3}}{4 Y b d^{3}}\)
Here, all alphabets are in their usual meanings.

Section – B (3 Marks Each)

Question 4.
If the coefficient performance of a refrigerator is 5 and operates at the room temperature (27°C), find the temperature inside the refrigerator.
Answer:
Given: β = 5, T₁ = 27°C = 27° + 273 = 300 K
Coefficient performance of refrigerator,
β = \(\frac{T_{2}}{T_{1}-T_{2}}\)
5 = \(\frac{T_{2}}{300-T_{2}}\) ⇒ T₂ = 1500 – 5T₂
T₂ 5T₂ = 1500
6T₂ = 1500
T₂ = \(\frac{1500}{6}\) = 250K
T₂ = 250 – 273
T₂ = -23° C

Question 5.
For Brownian motion of particles of suspensions in liquid. Answer the following :
(a) What should be the typical size of suspended particles ?
(b) Bombardments of the suspended particles by molecules of the liquid are random. We should then expect equal no. of molecules hitting a suspended particle from all directions. Why is the net impact not zero ?
(c) Can the assembly of suspended particles be considered a ‘gas’ of ‘heavy molecules’ ? If so, what will be the temperature of this gas if temperature of the liquid is T ?
Answer:
(a)10^-6m.
(b) The average number of molecules hit in different directions so their net impact is not zero.
(c) Yes, since the heavy gas is in thermal equilibrium with the liquid, its temperature is equal to the temperature of liquid, i.e., T.

Question 6.
A truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is 800 N. How much has the cable stretched? (Young’s modulus for steel is 2 × 10¹¹ Nm^-2.)
Answer:
Given:
Steel cable’s length, l = 9.1 m
Radius, r = 5 mm = 5 × 10^-3 m.
Tension in cable, F = 800 N
Young’s modulus = 2 × 10¹¹ N/m²
Youngf s modulus,
Y = \(\frac{F}{A} \times \frac{l}{\Delta l}\)‘
or
Δl = \(\frac{F}{\pi r^{2}} \times \frac{l}{Y}\)
= \(\frac{800 \times 9.1}{3.14 \times\left(5 \times 10^{-3}\right)^{2} \times 2 \times 10^{11}}\)
= 4.64 × 10^-4 m

Question 7.
Discuss strings stretched between fixed points.
Answer:
Let a spring be stretched between two points as shown in figure. Vibrations will set up in this string when it is disturbed, say from middle. The figure given below shows that vibration set up in this string appears to be similar to a half wave having wavelength \(\frac{\lambda}{2}\).

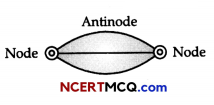
Length of the spring l = \(\frac{\lambda}{2}\)
or λ = 2l …………… (i)
If T is tension in the string and m is mass per unit length of the string, then velocity of disturbance is given by
υ = \(\sqrt{\frac{\mathrm{T}}{m}}\) ……………. (ii)
also υ = \(\frac{\text { Wavelength }}{\text { Time }}\)
= Wavelength x Frequency
= λf
or υ = 2l x f using equ (i)
or f = \(\frac{v}{2 l}\) ……………. (iii)
From equation (ii) and (iii)
f = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mathrm{M}}}\) (∵ υ = \(\sqrt{\frac{\mathrm{T}}{\mathrm{M}}}\))

Question 8.
State Pascal’s law of transmission of fluid pressure. Explain how is Pascal’s law applied in a hydraulic lift, (with suitable diagram).
OR
A razor blade can be made to float on water. What forces act on this blade ?
Answer:
Pascal law : If gravity effect is neglected the pressure at every point of liquid in equilibrium at rest is same.

Hydraulic lift: It is used to lift the heavy loads. Its working is based on Pascal’s law. A simple hydraulic lift is shown in Figure. Here C and D are two cylinders of different areas of cross section. They are connected to each other with a pipe E. Each cylinder is provided with airtight frictionless piston. Let a, and A be the areas of cross-sections of the pistons in C and D respectively, where a < < A. The cylinders are filled with an incompressible liquid.

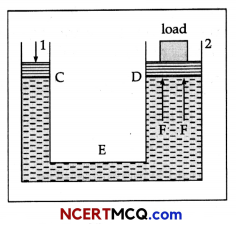
Let a downward force/be applied on the piston of C. Then the pressure exerted on the liquid, P = f/a.

Solutions
According to Pascal’s law, this pressure is transmitted equally to piston of cylinder D.
∴ Upward force acting on the piston of cylinder D will be
F = PA = \(\frac{f}{a}\) A = f\(\frac{\mathrm{A}}{a}\).
OR
When a razor blade is made to float on water, three forces act on the blade:

• Weight of the blade acting vertically downwards.
• Reaction on blade exerted by the liquid surface acting vertically upwards.
• Force of the surface tension on circumference of the blade acting tangentially to the liquid surface.

Question 9.
A standing wave is represented by y = 2Asin kx cos ωt. ff one of the component waves is y₁ = Asin (ωt – kx). What is the equation of the second component wave ?
Answer:
∴ y = 2Asin kx cos ωt
As 2sin Acos B = sin(A + B) + sin(A – B)
= Asin (kx + ωt) + Asin (kx – ωt)
According to superposition principle,
y = y₁ + y₂
and y₁ = Asin (ωt – kx)
= – Asin (kx – ωt)
y₂ = y – y₁ = 2Asin kx cos ωt + Asin (kx – ωt)
– Asin (kx + ωt) + 2Asin (kx – ωt)
= Asin (kx + ωt) – 2Asin (ωt – kx)

Question 10.
A particle moves with S.H.M. in a straight line. In the first second after starting from rest, it travels a distance x₁ cm and in the next second it travels a distance x₂ cm in the same direction. Prove that the
amplitude of oscillation is \(\frac{2 x_{1}^{2}}{\left(3 x_{1}-x_{2}\right)}\)
Answer:
As the particle starts from rest, it must start from the extreme position. Hence, when t = 0, x = r, where r is the required amplitude. 1
Using the relation, x = rcos ωt
or r – x₁ = rcos (ω × 1)
= rcos ω ………………. (i)
and r- (x₁ + x₂) = rcos (ω × 2)
= rcos 2ω
or r – x₁ – x₂ = r(2 cos² ω – 1) …….. (ii)
Solving (i) and (ii),
r = \(\frac{2 x_{1}^{2}}{3 x_{1}-x_{2}}\)

Question 11.
What is standing wave ? Give its characteristics.
OR
Obtain an equation of a progressive wave.
Answer:
Standing or stationary wave results when two progressive waves of same wavelength and amplitude travelling with same speed in opposite directions superimpose.
Characteristics:

1. Energy is not transferred from particle to particle.
2. Amplitude of vibration of particles is maximum at antinode and minimum (say zero) at nodes.
3. Time period of all particles is same except at nodes.
4. Wavelength and frequency of standing wave is same as that of the component wave.
5. Pressure variation is minimum at antinode and maximum at nodes.

OR
For a simple harmonic motion, displacement
y = r sin (ωt + Φ)
where r is amplitude, ω is angular velocity and Φ is phase difference
But ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πf
and Φ = \(\frac{2 \pi}{\mathrm{T}}\) x
where λ is wavelength and x is path difference.
∴ y = rsin 2π(\(\frac{t}{\mathrm{~T}}+\frac{x}{\lambda}\))

Section – C (5 Marks)

Question 12.
Case Study: Triple Point:
The temperature of a substance remains constant during its change of state (phase change). A graph between the temperature T and the Pressure P of the substance is called a phase diagram or P-T diagram.
The following figure shows the phase diagram of water and CO₂. Such a phase diagram divides the P-T plane into a solid-region, the vapour-region and the liquid-region. The regions are separated by the curves such as sublimation curve (BO), fusion curve (AO) and vaporisation curve (CO).

The points on sublimation curve represent states in which solid and vapour phases coexist. The point on the sublimation curve BO represent states in which the solid and vapour phases coexist.
Points on the fusion curve AO represent states in which solid and liquid phase coexist.

Points on the vaporisation curve CO represent states in which the liquid and vapour phases coexist.
The temperature and pressure at which the fusion curve, the vaporisation curve and the sublimation curve meet and all the three phases of a substance coexist is called the triple point of the substance.

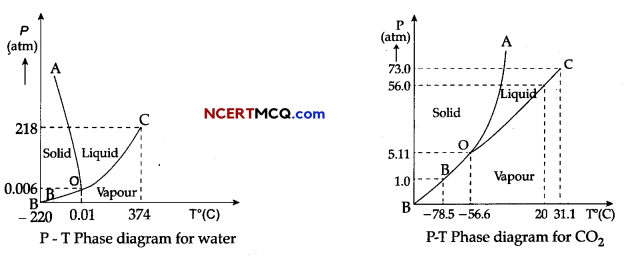
(i) Sublimation curve represents the coexistence of
(a) Solid and liquid state
(b) Solid and vapour state
(c) Liquid and vapour state
(d) Liquid, solid and vapour state [1]

(ii) The temperature and pressure at which all the three phases of a substance coexist is called
(a) Boiling point
(b) Freezing point
(c) Triple point
(d) Melting point [1]

(iii) During phase change of a substance
(a) The temperature remains constant
(b) The temperature changes very slowly
(c) The temperature changes very fast
(d) Both temperature and pressure change very slowly [1]

(iv) The triple point of water is:
(a) 0.01 °C at 0.006 atmosphere
(b) 0.01K at 0.006 atmosphere
(c) – 0.01K at 0.006 atmosphere
(d) – 0.01°C at 0.006 atmosphere [1]

(v) Triple point of CO₂ is
(a) – 78.5° C at pressure of 1 atm.
(b) -56.4° C at pressure of 5.11 atm.
(c) -56.4 K at pressure of 5.11 atm.
(d) – 78.5 K at pressure of 1 atm. [1]
Answer:
(i) Option (b) in correct.
Explanation: The points on sublimation curve represent states in which solid and vapour phases coexist. The point on the sublimation curve BO represent states in which the solid and vapour phases coexist.

(ii) Option (c) in correct.
Explanation: The temperature and pressure at which the fusion curve, the vaporisation curve and the sublimation curve meet and all the three phases of a substance coexist is called the triple point of the substance.

(iii) Option (a) in correct.
Explanation: The temperature of a substance remains constant during its change of state (phase change).

(iv) Option (a) in correct
Explanation: From graph, the triple pint of water is 0.01° C at 0.006 atmosphere pressure.

(v) Option (b) in correct.
Explanation: From graph, the triple pint of CO₂ is -56.4° C and a pressure of 5.11 atm.