CBSE Sample Papers for Class 12 Physics Term 2 Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 2 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B, and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

 SECTION – A
(Section A contains 3 questions of 2 marks each.)

Question 1.
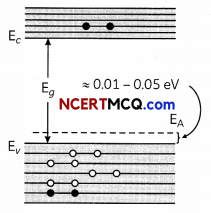
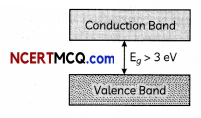
How is a p-type semiconductor formed? Draw energy band of p-type semiconductors and name the majority charge carriers in it. (2)
Answer:
1. If trivalent impurity atoms of B, Al, or In are doped in a pure semiconductor of Silicon or Germanium, we get a p-type semiconductor. Holes are the majority charge carriers in a p-type semiconductor. The diagram of energy band of p-type semiconductors is given below.

Related Theory
There are two types of dopants used for doping the tetravaLent Silicon or Germanium.
1. Pentavalent dopants which have five valence electrons like Arsenic, Antimony, and Phosphorus.
2. Trivalent dopants have three valence electrons like Indium, Boron, and Aluminium.

Question 2.
Photons, with a continuous range of frequencies, are made to pass through a sample of rarefied hydrogen.
Transitions of electrons are shown in figure:

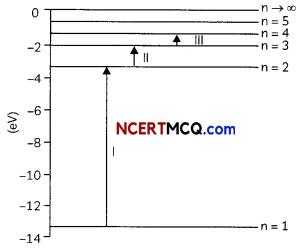
(A) Identify the spectral series, of the hydrogen emission spectrum corresponding to these lines.
(B) Which of these lines corresponding to absorption of radiation of maximum wavelength?
OR
Plot a graph showing the variation of stopping potential with the frequency of incident radiation for two different photosensitive materials having work functions W₂ and W₂ (W₁ > W₂).
On what factors does the (i) slope and (ii) intercept of the lines depend? (2)
Answer:
(A) Transition I → Lyman series
Transition II → Balmer series
Transition III → Paschen series of spectral absorption lines in the continuous spectrum.

(B) Energy of electron in hydrogen atom
E_n = \(-\frac{13.6}{n^{2}}\) eV
E₁ = -13.6 eV
E₂ = – 3. 4 eV and similarly we can find E₃, E₄, ……………..
For transition III energy absorbed is:
ΔE = E₄ – E₃ = 0.66 eV

which is least out of three transitions. Transition III corresponds to the absorption of radiation of maximum wavelength.
OR
The graph of stopping potential Vs and frequency (v) for two metals 1 and 2 is shown in fig.

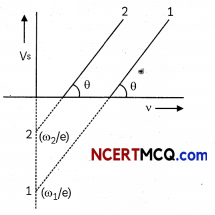
(A) Slope of graph tan θ= \(\frac{h}{e}\) and depends on h and e.
(B) Intersect of lines depend on the work function.

Question 3.
Distinguish between the metals and insulators on the basis of energy band theory. Why does a diamond behave as an insulator? (2)
Answer:
For metals, the valence band is completely filled and the conduction band have the possibilities,
either it is partially filled within extremely small energy gap between valence band and conduction band or it is empty, with two bands overlapping each other.

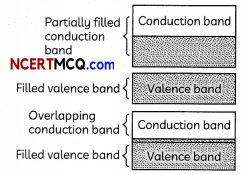
For insulators, the energy gap between the conduction and valence band are very large, also the conduction band is partially empty. When an electric field is applied across such a solid, the electrons find it difficult to acquire sufficient energy to jump to conduction band. There is a Large forbidden band of 6eV in diamond. It is difficult to excite the electrons from valence band to the conduction band. Due to the absence of free charges, diamond behaves as an insulator.

SECTION – B
(Section B consists of 8 questions of 3 marks each.)

Question 4.
(A) State Bohr’s postuLate to define stable orbits in hydrogen atoms. How does Louis de BrogUe’s hypothesis explain the stability of these orbits?
(B) A hydrogen atom initially in the ground state absorbs a photon which excites it to the n = 4 LeveL Estimate the frequency of the photon. (3)
Answer:
(A) Bohr’s postulate for stable orbits in hydrogen atom: An electron can revolve only in those circular orbits in which its angular momentum is an integral multiple of \(\frac{h}{2 \pi}\). where h is Planck’s constant.

If n is the principal quantum number of orbit, then an electron can revolve only in a certain orbits of definite radii. These are called stable orbits. Louis de Broglie’s explanation of stabiLity of orbits:

According to de Broglie. orbiting electron around the nucleus is associated with a stationary wave. Electron wave is a circular standing wave. Since destructive interference will occur if the standing wave does not close upon itself only those Louis de Brog lie waves exist for which the circumference of circular orbit Contains a whole number of wavelengths i.e., for orbit circumference of nth orbit as 2nπr_n
2πr_n = nλ
2πr_n = n \(\left(\frac{h}{m v}\right)\)
mvr_n = n \(\left(\frac{h}{2 \pi}\right)\)
which is the quantum condition proposed by Bohr.

(B) In ground state, n = 1
In excited state, n = 4
\(\frac{1}{\lambda}=R\left[\frac{1}{(1)^{2}}-\frac{1}{(4)^{2}}\right]\) where R is Rydberg constant
\(\frac{1}{\lambda}\) = 1.097 x 10⁷ x \(\frac{15}{16}\)
= 1.028 x 10⁷ m^-1
Frequency, v = \(\frac{c}{\lambda}\) = 3 x 10⁸ x 1.028 x 10⁷
= 3.09 x 10¹⁵ Hz.

Question 5.
(A) When p-n junction Is said to be reverse-biased, what will be the direction of flow of majority charge carriers?
(B) Which semiconductors are preferred to make LED and why?
(C) Give two advantages of using LED. (3)
Answer:
(A) A p-n junctión ¡s set to be reverse biased when its p-region is maintained at lower potential with respect to its n-region. i.e, p-end is connected with negative terminal, and n-end is connected with positive terminal In a reverse-biased p-n junction.
majority charge carriers move away from the junction.
(B) MateriaLs Like gaLLium phosphide (Gap) Gallium arsenide (GaAs), etc., are used.
They emit the maximum amount of energy in form of tight radiation.
(C) The following are the advantages of LEDs:
(i) They are operational at two voltages.
(ii) They are quick in action and their power consumption is Low.

Question 6.
What is meant by the size of nucleus? A nucleus of mass number 225 splits into two fresh nucLei having radius R = 1.1 x 10^-15 A^1/3 m, find the radii of the new nuclei formed. (3)
Answer:
The extremely small central core of the atom in which whole of the positive charge and practically the entire mass is confined is known as nucleus. Different nuclei differ in size. The radius of nuclei is directly proportional to A^1/3.
where A is its mass number.
Here A = 225, R = 1.1 x 10^-15 A^1/3 m
Let A₁ and A₂ be the respective mass number of two new nuclei formed.
A₁= \(\frac{3}{(3+2)}\) A
= \(\frac{3}{5}\) x 225
= 135
And,
A₂ = \(\frac{3}{(3+2)}\) A
=\(\frac{2}{5}\) x 225 = 90

R₁= 1.1 x 10^-15 A^1/3
= 1.1 x 10^-15 x 135^1/3
= 5.643 x 10^-15 m

R₂ = 1.1 x 10^-15 A^1/3
= 1.1 x 10^-15 x 90^1/3
= 4.93 x 10^-15 m.

Question 7.
State Huygens’ principLe. Using this principle draw a diagram to show how a plane wavefront incident at the interface of the two media gets refracted when It propagates from a rarer to a denser medium. Hence, verify Snell’s Law of refraction. (3)
Answer:
(A) Huygens’ Principle:
(i) Each point on the primary wavefront acts as a source of secondary wavelets, transferring out a disturbance in all directions in the same way as the original source of Light does.
(ii) The new position of the wavefront at any instant is the envelope of the secondary wavelets at that instant.

(B) Refraction on the basis of wave theory:
(i) Consider any point Q on the incident wavefront
(ii) Suppose when disturbance from point P on incident wavefront reaches point P’ on the refracted wavefront, the disturbance from point Q reaches Q’ on the refracting surface XY.

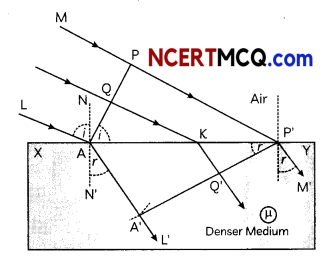
(iii) Since P’A’ represents the refracted wavefront, the time taken by light to travel from o point on incident wavefront to the corresponding point on refracted wavefront should always be the same. Now, time taken by Light to go from Q to Q will be

t = \(\frac{Q K}{c}+\frac{Q K}{v}\) ………………………… (i)

In right-angled ΔAQK,
∠QAK = i
∴ QK=AK sin i …………………………………. (ii)
In right-angled ΔP’Q’K.
∠Q’P’K = r
and Q’K = KP’ sin r …………………………. (iii)
Substituting (ii) and (iii) in equation (i).

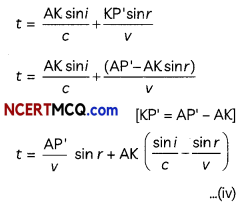
The rays from different points on the incident wave front will take the same time to reach the corresponding points on the refracted wave front i.e., given equation (iv) is independent of AK. It will happen so. if
\(\frac{\sin i}{c}-\frac{\sin r}{v}\) = 0
⇒ \(\frac{\sin i}{\sin r}=\frac{c}{v}\)
⇒ n = \(\frac{\sin i}{\sin r}\)
This is the Snells low for refraction of light.

Retated Theory
Wave theory explained Lows of reflection and refraction both.

Question 8.
Draw a labelled ray diagram of an astronomical telescope in the near-point adjustment position. A giant refracting telescope at an observatory has an objective Lens of Focal Length 15 m and an eyepiece of focal length 1.0 cm. If this telescope is used to view the Moon, find the diameter of the image of the Moon formed by the objective lens.
The diameter of the Moon is 3.48 x 10⁶ m and the radius of lunar orbit is 3.8 x 10⁶ m.
OR
ExpLain the refraction of Light through a glass-slab with a neat ray diagram. (3)
Answer:
Astronomical teLescope in near points adjustment

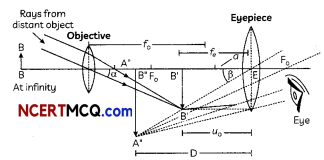
Here, f₀ = 15 m,
f_e=1 cm = 0.1 m
Diameter of moon,
d = 3.48 x 10⁶ m

Radius of lunar orbit
μ₀ = 3.8 x 10⁸ m
size of the image of moon I = ?
The angle subtended by the moon at the objective lens,
α = \(\frac{d}{\left|\mu_{0}\right|}\) ………………………….. (i)
And the angle subtended by the image of the moon at the objective lens,
β = \(\frac{I}{f_{0}}\) ……………………… (ii)

Both these angles in equations (i) and (ii) wift be equal.
∴ \(\frac{d}{\left|\mu_{0}\right|}=\frac{1}{f_{0}}\)
⇒ I = \(\frac{d \times f_{0}}{\left|\mu_{0}\right|}\)
= \(\frac{3.48 \times 10^{6} \times 15}{3.8 \times 10^{8}}\) m
= 13.73 x 10^-2 m
= 13.73 cm.
OR

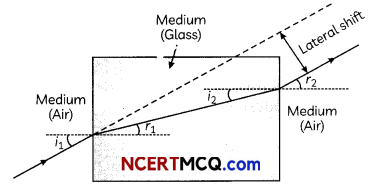
On entering into the glass medium-light ray bends towards the normal that is tight ray gets refracted on entering the gLass medium. After getting refracted this ray now travels through the glass slab and comes Out of the glass slab by refraction from the other interface boundary. Since ray goes from glass medium to air it again gets refracted and bends away from normal.

The incident ray and the emergent ray are parallel to each other. i₁ is the angLe of incidence, r₁ is the angLe of
refraction and r₂ is the angle of emergence. The angle of incidence and angle of emergence are equal as emergent ray and incident ray are parallel to each other. When a Lightray is incident normally to the interface of two media then there is no bending of tight ray and it goes straight through the medium.

Question 9.
In the study of a photoeLectric effect the graph between the stopping potential V and frequency y of the incident radiation on two different metals P and Q is shown below:
(A) Which one of the two metals has higher threshold frequency?
(B) Determine the work function of the metal which has greater value.
(C) Find the maximum kinetic energy of electron emitted by light of frequency 8 x 10¹⁴ Hz for this metal. (3)
Answer:
(A) Q has higher threshoLd frequency.
(B) Work function of Q
Φ_o = hv₀
hv0 = (6.6 x 10^-34) x \(\frac{6 \times 10^{14}}{1.6 \times 10^{-19}}\) eV
= 2.5 eV

(C) K_max = h(v – v₀)
= \(\frac{6.6 \times 10^{-34}\left(8 \times 10^{14}-6 \times 10^{14}\right)}{1.6 \times 10^{-19}} \mathrm{eV}\)
= \(\frac{6.6 \times 10^{-34} \times 2 \times 10^{14}}{1.6 \times 10^{-19}} \mathrm{eV}\)
K_max=0.83eV.

Question 10.
(A) Monochromatic Light of wavelength 589 nm is incident from air on a water surface. If μ for water is 1.33, find the wavelength, frequency, and speed of the refracted light.
(B) A doubLe convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature.
Find the radius of curvature required, if the focal length is 20 cm. (3)
Answer:
(A) Given: m= 1.33
λ_a= 589 nm
We know that,
μ = \(\frac{C}{V}\)
v = \(\frac{c}{\mu}\)
= \(\frac{3 \times 10^{8}}{1.33}\)
Speed, v = 2.26 x 10⁸ m/s

Frequency remains same.
∴ v = \(\frac{c}{\lambda_{a}}=\frac{3 \times 10^{8}}{589 \times 10^{-9}} \)
Frequency, v = 5.09 x 10¹⁴ Hz
Wavelength.
λ_w = \(\frac{\lambda_{a}}{\mu} \)
= \(\frac{589 n m}{1.33}\)
= 442.8 nm

(B) Given: μ= 1.55.
20 cm
We know that,

R = 20 x 0.55 x 2
R= 22 cm.

Question 11.
Which constituent radiation of the electromagnetic spectrum is used
(A) in radar
(B) to photograph internal part of a human body, and
(C) for taking photographs of the sky during night and foggy conditions?
Give one reason for your answer in each case.
OR
(A) When a convex Lens of Focal Length 30 cm is in contact with concave tens of focal length 20 cm, find out if the system is converging or diverging.
(B) Obtain the expression for the angle of incidence of a ray of light which is incident on the face of a prism of
refracting angle A so that it suffers total internal reflection at the other face. (Given the refractive index of the glass of the prism is μ.)
Answer:
(A) Microwaves are used .in the operation of radar because microwaves have small wavelengths and are not bent by objects coming in its path. Due to it, these waves can be sent in a particular direction as a beam signal.

(B) X-rays are used to photograph internal parts of a human body because X-rays are a quite short wavelengths. They can easily pass-through flesh but not bones.
(i) Infrared rays are used for taking photographs of the sky during night and foggy conditions because these
can easily pass-through fog and dark.
OR
(A) f₁= f_convex= 30 cm
f₂ = f_concave = – 20 cm
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
= \(\frac{1}{30}-\frac{1}{20} \)
= \(\frac{2-3}{60}\)
\(\frac{1}{f}=-\frac{1}{60}\)
[∴ concave (diverging) lens)]

(B) μ = \(\frac{\sin \left(\frac{\delta_{\min }+A}{2}\right)}{\sin \frac{A}{2}}\)
Let C is the critica angle,
sin C = \(\frac{1}{\mu}\)

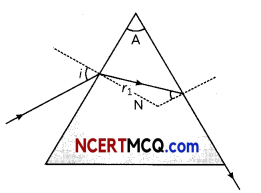
r₁+r₂ = A
r₁+C = A
r₁ = A – C
μ = \(\frac{\sin i}{\sin r_{1}}\)
⇒ sin i = μ sinr₁
sin i = μ sin(A-C)
i = sin^-1μ sin(A-C)

SECTION – C
(Section C consists one case study-based quote of 5 marks.)

Question 12.
If the setup of Young’s doubLe slit experiment is immersed in a liquid then the Wavelength of the Light gets changed. Since an immersion frequency remains unchanged, velocity decreases hence, waveLength decreases. Now, alt those parameters which are dependent on wave Length will be affected. If the fringe width is air in \(\frac{\lambda D}{d}\) then in Light it will be \(\frac{\lambda D}{\mu d}\) in the same way, the angular fringe width also changes and the position of cringes on-screen aIs changes. (3)

(A) In Young’s experiment when sodium Light of waveLength 5893A° is used, then 62 fringes are seen in the field of view. Instead, if violet Light of waveLength 4358A° is used, then the number of fringes that will be seen in the field of view will be:
(a) 54
(b) 64
(c) 74
(d) 84
at x = 0. The third maximum (taking the central maximum as zero maximum) will be at x equal to:
(a) 1.67 x 10^-2 m
(b) 1.5 x 10^-2 m
(c)O.5 10^-2m
(d) 5.0 10^-2 m

(C) In Young’s experiment, the ratio of maximum to minimum intensities of the fringe system is 4:1. The amplitudes of the coherent sources are in the ratio:
(a) 4:1
(b) 3:1
(c) 2:1
(d) 1:1

(D) The displacement of two Interfering Light waves are y₁ = 4sinωt and Y₂ = 3sinω \(\left(\frac{\omega t+\pi}{2}\right)\) .The ampLitude of the resultant wave is:
(a) 5
(b) 7
(c) 1
(d) 0
(E) In Young’s experiment, tight of waveLength 4000Å is used to produce bright fringes of width 0.6 mm, at a
dipped in a Liquid of refractive index 1.5, then the fringe width will be:
(a) 0.2 mm
(b) 0.3 mm
(c) 0.4 mm
(d) 1.2 mm (5)
Answer:
(A) (d) 84
Explanation: From Young’s double slit experiment,
λ₁ = 5893 Å
λ₂= 4359 Å
\(\frac{n_{1} \lambda_{1} D}{d}\) = \(\frac{n_{2} \lambda_{2} D}{d}\)
The above condition is total extent of fringes is constant for both wavelengths.
\(\frac{62 \times 5893 \times 10^{-10} \times \mathrm{D}}{d}=\frac{n_{2} \times 4359 \times 10^{-10} \times \mathrm{D}}{d}\)
n₂ = \(\frac{62 \times 5893}{4359}\)
= \(\frac{365366}{4359}\) = 83.8
n₂ = 84

Related Theory:
In Young’s double-slit, experiment the number of fringes ate inversely proportional to the fringe width.
(B) (b) 1.5 x 10^-2 m
Explanation: x = (n) \(\lambda \frac{\mathrm{D}}{d} \)
= 3 x 5000 x 10^-10 x \(\frac{2}{0.2 \times 10^{-3}}\)
= 1.5 x 10^-2 m = 1.5 cm

Caution:
Students are often confused about the number of slits. In Young’s double-slit experiment two slits are there.
(C) (b) 3:1

Explanation: \(\frac{I_{(m a x)}}{I_{(m i n)}}=\frac{\left(a_{1}+a_{2}\right)^{2}}{\left(a_{1}-a_{2}\right)^{2}}\)
⇒ \(\frac{4}{1}=\frac{\left(a_{1}+a_{2}\right)^{2}}{\left(a_{1}-a_{2}\right)^{2}}\)

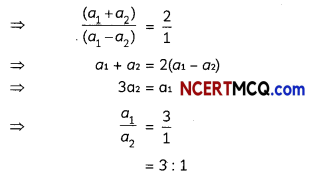
Related Theory:
In Young’s experiment, intensity of tight is directly proportional to the square of the amplitude.
(D) (a) S
Explanation: Here,
Φ = \(\frac{\pi}{2}\)
Amplitude of first wave = A₁ = 4
Amplitude of second wave = A₂ = 3
Resultant = \(\sqrt{\left[(4)^{2}+(3)^{2}\right]}\)
= 16 + 9 = 5cm.

(E) (c) 0.4 mm
Explanation: Fringe width.

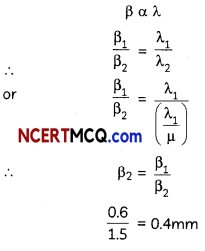
Caution:
Students are often confused in the relation of fringe width and wavelength of Light. Here, fringe width is
directly proportional of a wavelength of Light.