CBSE Sample Papers for Class 12 Physics Term 2 Set 8 with Solutions

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 8 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 8 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A contains 3 questions of 2 marks each.)

Question 1.
What is ‘greenhouse effect’? State its importance for us.
OR
Explain the dual nature of radiation. (2)
Answer:
The sun’s rays warms the surface of earth. A part of the radiation which falls on the earth is reflected back into the space and only a part of it is absorbed. This trapped radiation further warms the earth. The trapping of radiation by the earth’s atmosphere is known as Greenhouse effect. Life would not have been possible without this process. Carbon dioxide is one of the gases responsible for this effect. Some other gases like methane, nitrous oxide and water vapours also contribute towards this process.
OR
Dual nature of radiation is:
(A) The phenomenon of radiation such as photoelectric effect, Compton effect, Stark effect, Raman effect etc can only be explained on the basis of particle nature of radiation.
(B) The phenomenon of radiation such as interference, diffraction, polarization, reflection, refraction etc. can be explained on the basis of wave nature of radiation. Therefore, radiation has dual character wave and particle wave.

Question 2.
Considering the V-l characteristics of a p-n diode answer the following questions.
(A) Why under reverse bias almost independent of the applied potential up to a critical voltage?

(B) Why does the reverse current show a sudden increase in the critical voltage? 2
Answer:
(A) In reverse biasing, the current of order micro ampere is due to the drifting of minority charge carriers from one region to another through the junction. A small applied voltage is sufficient t o s weep t he minority charge carriers through thejunction. Therefore, reverse current is almost independent of critical voltage.

(B) At critical voltage which is also known as breakdown voltage, a large number of covalent bonds break, resulting in the increase of large number of charge carriers. Hence current increases at voltage.

Related Theory
After the cut-in voltage, the diode current increases exponentially even for a very small increase in diode bias voltage. Here, the majority charge carriers feet negligible resistance at the junction.

Question 3.
Two convex lenses of same focal length but of aperture A₁ and A₂ (A₂ > A₁), are used as the objective lenses in two astronomical telescopes having identical eyepieces. What is the ratio of their resolving power? Which telescope will you prefer and why? Give reason. (2)
Answer:
Resolving power of a telescope is proportional to its aperture, and is given by a relation, Therefore, the telescope with objective of aperture A₁ should be preferred for viewing as this would:
(A) give a better resolution.
(B) has a higher light gathering power of telescope.

SECTION – B
(Section B consists of 8 questions of 3 marks each.)

Question 4.
Why is the mass of a nucleus always less than the sum of masses of constituents? If the total number of protons and neutrons in a nuclear reaction is conserved, then how is the energy absorbed or evolved in reaction? (3)
Answer:
When nucleons combine to form nucleus, some mass is converted into binding energy in accordance with mass-energy equivalence relation. Hence, the mass of the nucleus is less than that of nucleons. The number of protons and number of neutrons are the same before a nuclear reaction and different after a nuclear reaction. This difference is called the mass defect.. It is denoted by ΔM.
ΔM =[ Zm_p+( A – Z)m_n ] – M
Einstein’s mass energy relation can be express this mass difference in terms of
ΔE_b = ΔMc²
This shows that if a certain number of neutrons and protons are brought together to form a nucleus of a certain charge and mass, an energy will be released in the process. That energy is termed as binding energy. If we separate a nucleus into its nucleons we would have to transfer a total energy to AEb, to the particles.

Question 5.
(A) When violet light is incident of a lens instead of red light, how does the focal length changes?
(B) Why does bluish colour predominate in a clear sky?
(C) Why does sun appear red at sunrise and sunset? (3)
Answer:
(A) Refractive index of a material is inversely proportional to the wavelength of the incident light. So, the focal length will decrease with decrease in wavelength according to the Lens maker formula,
\(\frac{1}{f}\) = (μ – 1)(\(\frac{1}{R_{1}}-\frac{1}{R_{2}}\))
Therefore, when violet light replaces the red light, then due to increase in wavelength, the focal length of the lens decreases.

(B) While light from the sun reaches the atmosphere that is comprised of the tiny particles of the atmosphere. These act as a prism and cause the different components to scatter. As blue light travels in shorter and smaller waves in comparison to the other colours of the spectrum, it is scattered the most, causing the sky to appear bluish.

(C) Sun appears red at sunrise and sunset due to the Least scattering of red light as it has the longest wavelength.

Related Theory
w Scattering of light is the phenomenon in which light is deflected from its path due to its interaction with the particles of the medium through which it passes.

Question 6.
What do you mean by Q-value of nuclear reaction?
OR
Explain the colours in thin film and state the uses of interference. (3)
Answer:
Q vo[ue of reaction is calculated from Einsteins mass energy equivalence relation. E = mc², It may be positive or negative. A nuclear reaction in which Q vaLue is positive, energy is released. Such a reaction is caL[ed exoergic. A nuclear reaction in which Q vaLue is negative, energy has to be supplied beftwe the reaction occurs. Such a reaction is called endoergic.

When white light is incident on a thin film (like oil film on the surface of water or a soap bubble) then interference takes place between the waves reflected from its two surfaces and waves refracted through it. The intensity becomes maximum and minimum as a result of interference and colours are seen. The source of light must be an extended source. The colours obtained in reflected and transmitted light are mutually complementary. The colours obtained in thin films are due to interference whereas those obtained in prims are due to dispersion.

The thin layer of oil on water and soap bubbles shows different colours due to interference of waves reflected from two surfaces of their films. Here we get two coherent beams by division of amplitude making use of partial reflection and partial refraction.

The interference effect can be used to determine the wavelength of Light precisely. It can be used to determine refractive index or thickness of transparent sheet. It is also used in holography to produce three-dimensional images.

Question 7.
(A) How does one understand the temperature dependence of resistivity of semiconductor?
(B) Calculate the resistance of the diode at (A) I = 15 mA and at (B) V = -10 V with the help of V-l characteristic of a silicon diode given below.

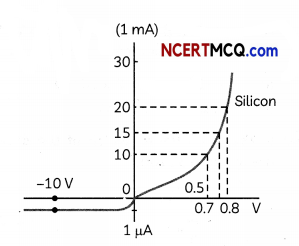
Answer:
(A) When temperature increases, covalent bonds of neighbouring atom breaks and charge carriers become free to cause conduction, so resistivity of semiconductor decreases with the rise of temperature.

(B) (i) From the given curve, voltage,
V = 0.7 V for current
I = 15 mA for voltage
Resistance= \(\frac{V}{I}\) = \(\frac{0.7}{15 \times 10^{-3}}\)
= 46.66 Ω

(ii) For V =-10V,
we have I = -1 μA
= -1 × 10^-6A
R = \(\frac{10}{1 \times 10^{-6}}\)
= 1.0 × 10⁷Ω

Caution
If the junction does not permit the flow of current, the diode is known to be at zero bias conditions and voltage is zero.

Question 8.
The intensity of central maxima (0) in YDSE is l_o. If the distance OP equals to \(\frac{1}{3}\) rd of fringe width, then show that the intensity at a point p would be \(\frac{I_{0}}{4}\)

Answer:
Given that
OP = Y_n
OP is equal to \(\frac{1}{3}\) rd of fringe width at the pattern.
Y_n = \(\frac{1}{3}\left(\frac{D \lambda}{d}\right)\)
\(\frac{d Y_{n}}{D}=\frac{\lambda}{3}\)
Phase difference,
ΔΦ = \(\frac{2 \pi}{\lambda} \times \frac{\lambda}{3}\)
= \(\frac{2 \pi}{3}\)

If the intensity at central fringe is I_o, then intensity at a point P, where phase difference is ΔΦ is given by,
I = I_o cos²ΔΦ
I = I_o (-cos\(\frac{\pi}{3}\))²
I = I_o(-\(\frac{1}{2}\))²
= \(\frac{\mathrm{I}_{0}}{4}\)
The intensity at point P would be \(\frac{\mathrm{I}_{0}}{4}\) .

Question 9.
A triangular prism of refracting angle 60° is made of a transparent material of refractive
index 2√3 A ray of light is incident normally on the face KL as shown in the figure. Trace the path of the ray as it passes through the prism and calculate the angle of emergence and angle of deviation.

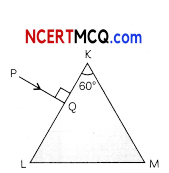
A convex lens of focal length 30 cm is placed coaxially in contact with a concave lens of focal length 40 cm. Determine the power of the combination. Will the system be converging or diverging in nature? (3)
Answer:
From diagram it is clear that incidence angle at face KM is 60°.

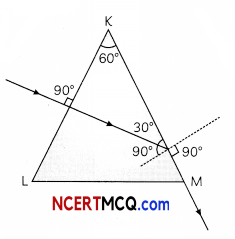
sin C \(\frac{1}{\mu}\) = \(\frac{\sqrt{3}}{2}\)
Hence, critical angle is also 60°.
Therefore, incident light ray will not emerge from KM face due to total internal reflection at this face. Hence, it will move along face KM Angle of emergence = 90°.
Hence angle of deviation = 30° (from fig.)
OR
focal length of convex lens,
f₁ = + 30 cm
= 0.30 m
Focal length of concave lens
f₂ = – 40 cm
= – 0.40 m
Equivalent focal length
\(\frac{1}{\mathrm{~F}}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
= \(\frac{1}{30}+\frac{1}{(-40)}\)
= \(\frac{40-30}{1200}=\frac{1}{120}\)
∴ F = 120 m
= 1.2 m
∴ Power of the combination,
p = \(\) = 0.83D
The focal length of combination = 1.2 m = 120 cm. As the focal length is positive the system will be converging in nature.

Question 10.
(A) How does one explain the emission of electrons from a photosensitive surface with the help of Einstein’s photoelectric equation?
(B) The work function of the following metals is given: Na = 2.75 eV, K = 23 eV, Mo = 4.17 eV and Ni = 5.15 eV. Which of these metals will not cause photoelectric emission for radiation of wavelength 3300 A from a laser source placed 1 m away from these metals ? What happens if the laser source is brought nearer and placed 50 cm away? (3)
Answer:
(A) According to Einstein’s photoelectric equation,
hv = hv₀ + E_max
E_max = hv- hv₀
E_max = h(v – V₀)
If v < v₀ then Emax will be negative so, no emission takes place.

If v > v₀ then E_max will be positive and directly proportional to □ so, emission takes place.

(B) E = \(\frac{h c}{\lambda}\)
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{3300 \times 10^{-10} \times 1.6 \times 10^{-19}}\)
E = 3.76 eV

The work function of Na and K is less than the energy of incident radiation. Therefore, Na and K will cause photoelectric emission while M0 and Ni will not cause photoelectric emission. There will be no effect on photoelectric emission if the source is brought nearer.

Question 11.
(A) Using Bohr’s second postulate of quantization of orbital angular momentum show that the circumference of the electron in the nth orbital state in hydrogen atom is n times the de Broglie wavelength associated with it.

(B) The electron in hydrogen atom is initially in the third excited state. What is the maximum number of spectral lines which can be emitted when it finally moves to the ground state? 3
Answer:
(A) According to Bohr’s second postulate of quantization, the electron can revolve around the nucleus only in those circular orbits in which the angular momentum of the electron is integral multiple of \(\frac{h}{2 \pi}\) where h is Planck’s constant (= 6.62 × 10^-34 Js).
So, if m is the mass of electron and v is the velocity of electron in permitted quantized orbit with radius r then
mvr = n \(\frac{h}{2 \pi}\) ……….(i)
Where n is the principal quantum number and can take integral values like
n = 1, 2, 3,…
This is the Bohr’s quantization condition. Now, de-Broglie wavelength is given as,
λ = \(\frac{h}{m v}\)
Where λ = Wavelength of wave associated with electron
m = Mass of the electron
h = Planck’s constant
mv = \(\frac{h}{\lambda}\)
or mvr = \(\frac{h r}{\lambda}\) ……………. (ii)
From equation (i) and (ii)
∴ \(\frac{h}{\lambda} r=\frac{2 h}{2 \pi}\)
\(\frac{r}{\lambda}=\frac{n}{2 \pi}\)
2πr = nλ
Now, circumference of the electron in the n^th orbital state of Hydrogen atom with radius r is nλ.

(B) If n is quantum number of the highest energy level involved in the transitions, then the total number of possible lines emitted is
N = \(\frac{n(n-1)}{2}\)
Third excited state means fourth energy level i.e., n = 1. So, highest number is n = 4.
Thus, possible spectral lines
N = \(\frac{4(4-1)}{2}\)
= \(\frac{4 \times 3}{2}\) = 6
The maximum possible number of spectral lines is 6.

SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
Due to movement of holes and electrons along the electric field sets up current. There are few basic features of forward biasing. Within the junction diode the current is due to both types of majority charge carriers but in external circuit it is due to electrons only. The current is due to diffusion of majority charge carriers through the junction and is of the order of milliamperes. In the same way the current is set up diode is reverse biased. There are two basic features of reverse biasing. Within junction diode the current is due to both types of minority charge carriers but in external circuit it is due to electrons only. The current is due to minority charge carriers through the junction and is very small of the order of microampere.


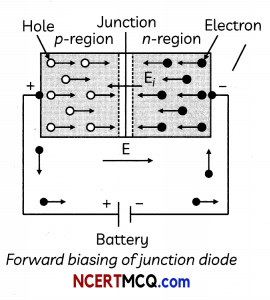
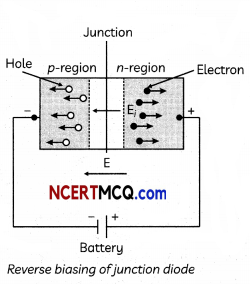
(A) When the forward bias voltage of a diode is changed from 0.6 V to 0.7 V, the current changes from 5 mA to 15 mA. Then its forward bias resistance is:
(i) 0.01
(ii) 0.1
(iii) 10.0
(iv) 100.00

(B) In the circuit, if the forward voltage drop for the diode is 0.5 V, the current will be:
0.5 V

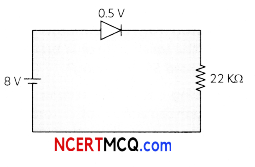
(i) 3.4 mA
(ii) 2 mA
(iii) 2.5 mA
(iv) 3 mA

(C) In a reverse biased diode when the applied voltage changes by 1 V, the current is found to change by 0.5 The reverse bias resistance of the diode is:
(i) 2 × 10⁵ Ω
(ii) 2 × 10⁶ Ω
(iii) 200 Ω
(iv) 2Ω

(D) In the given figure, which of the diodes are forward biased?

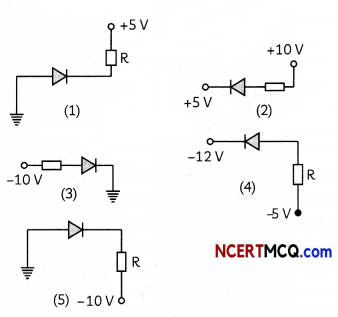
(i) 1, 2, 3
(ii) 2,4, 5
(iii) 1, 3, 4
(iv) 2, 3, 4

(E) In a diode, when there is a saturation current, the plate resistance will be:
(i) Data insufficient
(ii) Zero
(iii) Some finite quantity
(iv) Infinite quantity (5)

(A) (c) 10
Explanation: Forward biased resistance
\(\frac{\Delta V}{\Delta I}\) = \(\frac{0.7-0.6}{(15-5) \times 10^{-3}}\)
= \(\frac{0.1}{10 \times 10^{-3}}\) = 10Ω

Caution
The resistance in reverse bias is different from forward bias. Forward bias resistance is low whereas reverse bias resistance is high.

(B) (a) 3.4 mA
Explanation: When diode is forward biased, then there is a small voltage drop across it
i = \(\frac{V-V^{\prime}}{R}\)
Given, V = 8 volt,
V’ = 0.5 volt,
R = 2.2 kΩ
= 2.2 × 10³Ω
∴ i = \(\frac{8-0.5}{2.2 \times 10^{5}}=\frac{7.5 \times 10^{-5}}{2.2}\)
= 3.4 × 10^-3 A
= 3.4 mA

Related Theory
For forward bias, the voltage of an anode is greater than cathode and for reverse bias, the voltage for cathode is greater than an anode.

(C) (b) 2 x 10⁶Ω
Explanation: Reverse resistance
= \(\frac{\Delta V}{\Delta l}\) = \(\frac{1}{0.5 \times 10^{-6}}\)
= 2 x 10⁶ Ω

(D) (b) 2, 4, 5
Explanation: In figure 2, 4 and 5 P-crystals are more positive as compared to N- crystals.

(E) (d) Infinite quantity
Explanation: We know that plate resistance is given by:
∴ r_p = \(\frac{\Delta V}{\Delta l}\)
where ΔV is change in voltage and Δl is change in current.
Also, at saturation change in current is zero.
∴ r_p = \(\frac{\Delta V}{0}\) = ∞

Hence, plate resistance will be infinite.