Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 9 Ray Optics and Optical Instruments. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.
Class 12 Physics Chapter 9 Important Extra Questions Ray Optics and Optical Instruments
Ray Optics and Optical Instruments Important Extra Questions Very Short Answer Type
Question 1.
When light undergoes refraction at the surface of separation of two media, what happens to its frequency/wavelength?
Answer:
There is no change in its frequency, but its wavelength changes.
Question 2.
Define the refractive index.
Answer:
The Refractive index of a medium is defined as the ratio of the speed of light in a vacuum to the speed of light in the given medium.
Question 3.
What is the distance between the objective and eyepiece of an astronomical telescope in its normal adjustment?
Answer:
Distance between objective and eyepiece of telescope = fo + fe
Question 4.
Name the phenomenon responsible for the reddish appearance of the sun at sunrise and sunset.
Answer:
Atmospheric refraction.
Question 5.
What are the two main considerations that have to be kept in mind while designing the ‘objective’ of an astronomical telescope?
Answer:
Two main considerations are
- Large light gathering power
- Higher resolution (or resolving power)
Question 6.
Under what condition does a biconvex lens of glass having a certain refractive index act as a plane glass sheet when immersed in a liquid? (CBSE Delhi 2012)
Answer:
When the refractive index of the liquid is equal to the refractive index of a glass of which the lens is made.
Question 7.
Write the relationship between the angle of incidence ‘i’, angle of prism ‘A’ and angle of minimum deviation for a triangular prism. (CBSE Delhi 2013)
Answer:
2i = A + δm
Question 8.
Why can’t we see clearly through the fog? Name the phenomenon responsible for it. (CBSE Al 2016)
Answer:
Because it scatters light. Scattering of light.
Question 9.
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light? Give reason. (CBSE AI 2017)
Answer:
It decreases as δm ∝ \(\frac{1}{λ}\)
Question 10.
The objective lenses of two telescopes have the same apertures but their focal lengths are in the ratio 1: 2. Compare the resolving powers of the two telescopes. (CBSE AI 2017C)
Answer:
Same as resolving power does not depend upon the focal length of lenses.
Question 11.
An object is kept in front of a concave lens. What is the nature of the image formed? (CBSE Delhi 2017C)
Answer:
Virtual and erect.
Question 12.
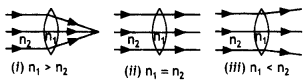
The refractive index of the material of a concave lens is n1. It is immersed in a medium of refractive index n2. A parallel beam of tight is incident on the lens. Trace the path of the emergent rays when n2 > n1.
Answer:
The path of rays is as shown
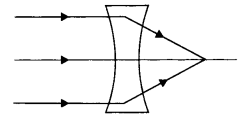
Question 13.
A convex lens made of glass of refractive index μL is immersed in a medium of refractive index μm. How will the lens behave when μL < μm?
Answer:
The lens will continue to behave as a convex lens.
Question 14.
The image of an object formed by a lens on the screen is not in sharp focus. Suggest a method to get clear focusing of the image on the screen without disturbing the position of the object, the lens or the screen.
Answer:
Limit the field of view of the lens by using a blackened glass having a small circular hole in the middle.
Question 15.
In the figure given below, the path of a parallel beam of light passing through a convex lens of refractive index ng kept in a medium of refractive index nm is shown. Is (i) ng = nm or (ii) ng > nm, or (iii) ng < nm?
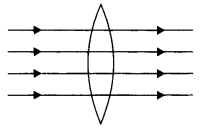
Answer:
As the rays of light do not suffer any deviation, therefore ng = nm.
Question 16.
In the figure path of a parallel beam of light passing through a convex lens of refractive index ng kept in a medium of refractive index, nm is shown. Is (i) ng = nm or (ii) ng > nm, or (iii) ng < nm?
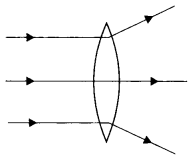
Answer:
As the rays of light diverge, therefore ng < nm.
Question 17.
The refractive index of the material of a concave lens is μ1. It is immersed in a medium of refractive index μ2. A parallel beam of light is incident on the lens. Trace the path of emergent rays when μ2 < μ1.
Answer:
The path of rays is as shown below.
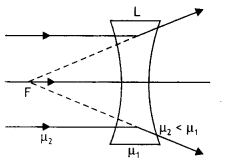
Question 18.
Suppose that the lower half of the concave mirror’s reflecting surface is covered with an opaque (non-reflective) material. What effect will this have on the image of an object placed in front of the mirror?
Answer:
The image of the whole object will be formed. However, as the area of the reflecting surface has been reduced the intensity of the image will below (in this case, half).
Question 19.
For the same value of angle of incidence, the angles of refraction in three media A, B and C are 15°, 25° and 35° respectively. In which medium would the velocity of light be minimum? (CBSE Al 2012)
Answer:
Medium A.
Question 20.
When red light passing through a convex lens is replaced by the light of blue colour, how will the focal length of the lens change? (CBSE AI 2013C)
Answer:
It will decrease.
Question 21.
A biconvex lens made of a transparent material of refractive index 1.25 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason. (CBSE AI 2014)
Answer:
The diverging lens as its focal length will become negative.
Question 22.
A concave lens of refractive index 1.5 is immersed in a medium of refractive index 1.65. What is the nature of the lens? (CBSE Delhi 2015)
Answer:
It will behave as a convex lens.
Question 23.
Why can’t we see clearly through a fog? Name the phenomenon responsible for it. (CBSE AI 2016)
Answer:
Because it scatters light. Scattering of light.
Question 24.
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light? Give reason. (CBSE AI 2017)
Answer:
It decreases as δm ∝ \(\frac{1}{λ}\)
Question 25.
The objective lenses of two telescopes have the same apertures but their focal lengths are in the ratio 1: 2. Compare the resolving powers of the two telescopes. (CBSE AI 2017C)
Answer:
Same as resolving power does not depend upon the focal length of lenses.
Question 26.
An object is kept in front of a concave lens. What is the nature of the image formed? (CBSE Delhi 2017C)
Answer:
Virtual and erect.
Question 27.
A convex lens is held in water. What change, if any, do you expect In its focal length?
Answer:
Focal Length of the given Lens increases in accordance with tens maker’s formula
\(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
This is because wμg aμg
Question 28.
Violet light is incident on a converging lens of focal length f. State with reason, how the focal length of the lens will change 1f the violet light is replaced by a red light.
Answer:
As μr < μv hence in accordance with the relation
\(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) focal Length of Lens for red colour will be more.
Question 29.
What is the minimum value of the refractive index of the prism shown in the figure below?
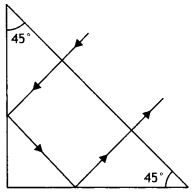
Answer:
μ = \(\frac{1}{\sin i_{c}}=\frac{1}{\sin 45^{\circ}}=\frac{1}{\sqrt{2}}\)
Question 30.
How does the resolving power of a telescope change on decreasing the aperture of its objective lens? Justify your answer.
Answer:
As the resolving power of a telescope is \(\frac{D}{1.22λ}\) hence on decreasing the aperture of its objective lens, the resolving power of the telescope decreases in the same ratio.
Question 31.
What will happen to a ray of light incident normally on the interface of air and glass?
Answer:
It will pass un-deviated into the glass.
Question 32.
What is the speed of light in glass having a refractive index of 1.5?
Answer:
Speed of light in glass v = c/n = 3 × 108 / 1.5 = 2 × 108 m s-1
Question 32.
Light of wavelength 600 nm in air enters a medium of refractive index 1.5. What will be its frequency in the medium?
Answer:
Frequency does not change when light moves from one medium into another. Therefore frequency of light
v = \(\frac{c}{\lambda}=\frac{3 \times 10^{8}}{600 \times 10^{-9}}\) = 5 × 1014 Hz
Question 34.
How does the focal length of a convex lens change if monochromatic red light Is used instead of monochromatic blue
light?
Answer:
Focal Length increases, i.e. fr > fv.
Question 35.
Two thin lenses of power + 5 D and – 3 D are in contact. What Is the focal length of the combination?
Answer:
Here P = P1 + P2 = + 5 – 3 = + 2 D
Hence f = 1/P = ½ m = + 50 cm.
Question 36.
Use the maker’s formula to write an expression for the (relative) refractive index, μ, of the material in terms of its focal length, f and the radii of curvature, r1 and r2, of Its two surfaces.
Answer:
The formula is \(\frac{1}{f}\) = (μ – 1)\(\left(\frac{1}{r_{1}}-\frac{1}{r_{2}}\right)\)
Question 37.
Two thin lenses of power – 4 D and 2 D are placed in contact coaxially. Find the focal length of the combination. (CBSE Ai 2012C)
Answer:
Total power P = – 4 + 2 = – 2 D
Now f = 1/P = 1/ -2 = – 0.5 m
Question 38.
A convex lens is placed In contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens? (CBSE Delhi 2014)
Answer:
20 cm
Question 39.
The focal length of a biconvex lens is equal to the radius of curvature of either face. What is the refractive index of the material of the lens? (CBSEAI 2015)
Answer:
1.5
Using \(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
Given R1 = R
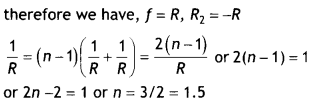
Question 40.
An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the ens are reversed? (NCERT Exemplar)
Answer:
No, the reversibility of the Lens does not change the lens formula.
Ray Optics and Optical Instruments Important Extra Questions Short Answer Type
Question 1.
The aperture of the objective lens of an astronomical telescope is doubled. How does it affect
(i) the resolving power of the telescope and
(ii) the intensity of the image? (CBSE Sample Paper 2018-19)
Answer:
The resolving power of a telescope is given by the expression \(\frac{D}{1.22λ}\).
(i) When the aperture of the objective lens is increased, the resolving power of the telescope increases in the same ratio.
(ii) The intensity of the image is given by the expression β ∝ D2, thus when the aperture is doubled, the intensity of the image becomes four times.
Question 2.
How does the resolving power of a compound microscope change on (a) decreasing the wavelength of light used, and (b) decreasing the diameter of the objective lens?
Answer:
The resolving power of a microscope is given by the expression RP = \(\frac{2 n \sin \theta}{\lambda}\)
(a) If the wavelength of the incident tight is decreased, the resolving power of the microscope increases.
(b)There is no effect of the decrease in the diameter of the objective on the resolving power of the microscope.
Question 3.
The layered lens shown in the figure is made of two kinds of glass. How many and what kinds of images will be produced by this lens with a point source placed on the optic axis? Neglect the reflection of light at the boundaries between the layers.

Answer:
Two images will be formed as the lens may be thought of, as two separate lenses of different focal lengths. The images will be surrounded by bright halos.
Question 4.
Monochromatic light is refracted from air into a glass of refractive index n. Find the ratio of wavelengths of the incident and refracted light.
Answer:
Using the relation λ1n1 = λ2n2 we have
\(\frac{\lambda_{1}}{\lambda_{2}}\) = n
Question 5.
Draw a labelled ray diagram to show the image formation in a compound microscope.
Answer:
The labelled diagram is as shown.
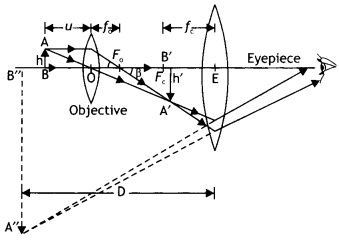
Question 6.
A ray of light while travelling from a denser to a rarer medium undergoes total internal reflection. Derive the expression for the critical angle in terms of the speed of light in the two media.
Answer:
Snell’s law can be used to find the critical angle. Now Snell’s law, when the ray moves from denser medium ‘b’ to rarer medium ‘a’, is given by

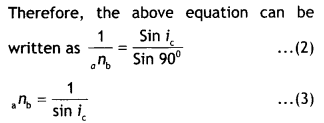
Now we know that n = \(\frac{c}{v}\) , substituting in the above relation we have
\(\frac{c}{v}=\frac{1}{\sin i_{c}}\) or sin ic = \(\frac{v}{c}\)
Question 7.
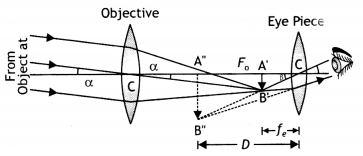
Draw a labelled diagram for a refracting type astronomical telescope. How will its magnifying power be affected by increasing for its eyepiece (a) the focal length and (,b) the aperture? Justify your answer. Write two drawbacks of refracting type telescopes. (CBSE Sample Paper 2018-19)
Answer:
The labelled diagram of the telescope is as shown in the figure.
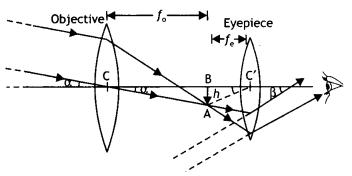
(a) The magnifying power of a telescope is given by M = \(\frac{f_{0}}{f_{\mathrm{e}}}\). If the focal length of the eyepiece is increased, it will decrease the magnifying power of the telescope.
(b) Magnifying power does not depend upon the aperture of the eyepiece. Therefore there is no change in the magnifying power if the aperture of the eyepiece is increased.
Drawbacks:
- Large-sized lenses are heavy and difficult to support.
- Large-sized lenses suffer from chromatic and spherical aberration.
Question 8.
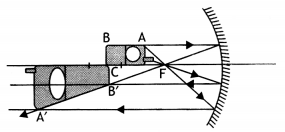
Draw a labelled ray diagram of a Newtonian type reflecting telescope. Write any one advantage over refracting type telescope.
Answer:
The labelled diagram is shown below.
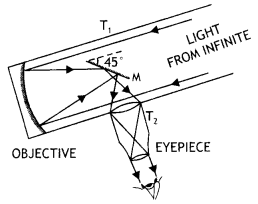
Due to the large aperture of the mirror as compared to a lens the image formed is much brighter than that formed by a refracting type telescope.
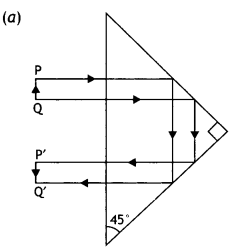
Question 9.
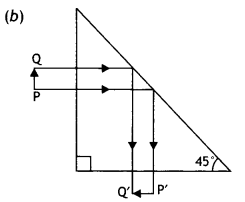
A right-angle crown glass prism with a critical angle of 41° is placed between the object PQ in two positions as shown in figures (a) and (b). Trace the path of rays from P and Q passing through the prisms in the two cases.
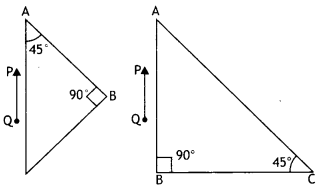
Answer:
The path of rays is as shown.
Question 10.
Write two conditions necessary for total internal reflection to take place.
Answer:
(a) The incident ray should travel from the denser to the rarer medium.
(b) The angle of incidence, in the denser medium, should be greater than the critical angle for the given pair of media.
Question 11.
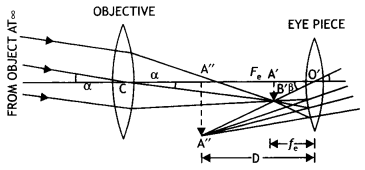
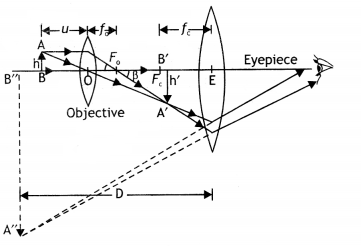
(a) Explain the working of a compound microscope with the help of a labelled diagram.
Answer:
A compound microscope is an instrument used to see highly magnified images of tiny objects.
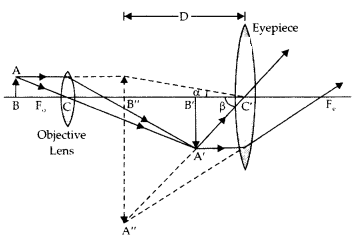
Working:
Let a tiny object AB be placed in front of the objective lens at a distance more than F0. Its real and enlarged image is formed at A ‘ B ‘. The image A’ B’ acts as an object for the eyepiece and forms the final image at A” B “,
i.e. at a distance D, the least distance of distinct vision.
(b) Write the considerations that you keep in mind while choosing lenses to be used as eyepiece and objective in a compound microscope. (CBSE 2019C)
Answer:
The objective and eyepiece should have a short focal length for large magnification.
Question 12.
Explain the working of a refracting telescope with the help of a labelled diagram. What are the main limitations of this type of telescope and how are these overcome in a reflecting telescope? (CBSE 2019C)
Answer:
Refracting telescope
Working:
When the rays of light are made to incident on the objective from a distant object, the objective forms the real and inverted image at its focal plane. The lens is so adjusted that the final image is formed at least distance of distinct vision or at infinity.
Limitations:
- Large-sized lenses are needed which are expensive.
- Large-sized lenses suffer from spherical aberration and distortions.
Reflecting telescope (To overcome limitations):
- Reflecting telescopes are free from chromatic aberration and spherical aberration is very small.
- They are less heavy and easier to support.
Question 13.
Explain why the colour of the sky is blue.
Answer:
As sunlight travels through the earth’s atmosphere, it gets scattered (changes its direction) by the atmospheric particles. Light of shorter wavelengths is scattered much more than light of longer wavelengths. (The amount of scattering is inversely proportional to the fourth power of the wavelength. This is known as Rayleigh scattering.)
Hence, the bluish colour predominates in a clear sky, since blue has a shorter wavelength than red and is scattered much more strongly. In fact, violet gets scattered even more than blue, having a shorter wavelength. But since our eyes are more sensitive to blue than violet, we see the sky blue.
Question 14.
Why does the sun look reddish during sunrise and sunset?
Answer:
At sunset or sunrise, the sun’s rays have to pass through a larger distance in the atmosphere (Figure). Most of the blue and other shorter wavelengths are removed by scattering. The least scattered light reaching our eyes, therefore, the sun looks reddish. This explains the reddish appearance of the sun near the horizon.
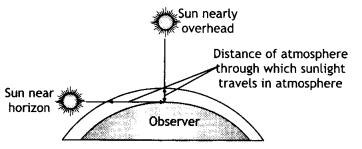
Question 15.
What are the two ways of adjusting the position of the eyepiece while observing the final image in a compound microscope? Which of these is usually preferred and why?
Answer:
The two ways
(a) Final image formed at least distance of distinct vision.
(b) Final image formed at infinity.
The second one is usually preferred as it helps the observer to observe the final image with his/her eye in a relaxed position.
Question 16.
Write the relation between the angle of incidence (i), the angle of emergence (e), the angle of the prism (A) and the angle of deviation (δ) for rays undergoing refraction through a prism. What is the relation between ‘i’ and ‘e’ for rays undergoing minimum deviation? Using this relation obtain an expression for the refractive index (μ) of the material of the prism in terms of ‘A’ and angle of minimum deviation.
Answer:
The relation is i + e = A + δm
In the minimum deviation position ∠i = ∠e
In the minimum deviation position we have A = r1 + r2 = r + r = 2r
or
r = A / 2
and i + i = A + δm
or
2i = A + δm
or
i = \(\frac{A+\delta_{m}}{2}\)
substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)
Question 17.
Draw a ray diagram showing the formation of the image by a concave mirror of an object placed beyond its centre of curvature. If the lower half of the mirror’s reflecting surface is covered, what effect will it have on the image? (CBSE AI 2011C)
Answer:
The required ray diagram is shown below.
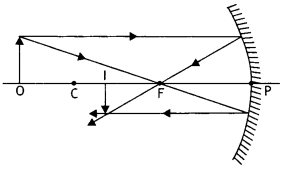
When the lower half of the mirror’s reflecting surface is covered, the intensity of the image will be reduced.
Question 18.
An object AB is kept in front of a concave mirror as shown in the figure.
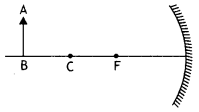
(a) Complete the ray diagram showing the image formation of the object.
(b) How will the position and intensity of the image be affected if the lower half of the mirror’s reflecting surface is painted black? (CBSE AI 2012)
Answer:
The completed ray diagram is as shown.
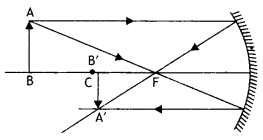
No change in the position of the image, but the intensity will decrease.
Question 19.
Draw a ray diagram to show the formation of the image by an astronomical telescope when the final image is formed at the near point. Answer the following, giving reasons
(a) Why the objective has a larger focal length and a larger aperture than the eyepiece?
(b) What would be the effect on the resolving power of the telescope if its objective lens is immersed in a transparent medium of the higher refractive index? (CBSE AI 2012C)
Answer:
The ray diagram is as shown.
(a) The objective lens has a large focal length and large aperture for large magnification and resolving power.
(b) The resolving power will increase as the wavelength of light used will decrease.
Question 20.
Two convex lenses of the same focal length but of aperture A1 and A, (A, < A1), are used as the objective lenses in two astronomical telescopes having identical eyepieces. What is the ratio of their resolving power? Which telescope will you prefer and why? Give reason. (CBSE Delhi 2011)
Answer:
The resolving power is directly proportional to the aperture. Therefore the ratio of their resolving power is RP = \(\frac{A_{1}}{A}\).
Since A1 > A therefore we will prefer the telescope with aperture A1 as it will gather a larger amount of light than the telescope of aperture A.
Question 21.
Which two of the following lens L1 L2 and L3 will you select as objective and eyepiece for constructing the best possible (a) telescope and (b) microscope. Give a reason to support your answer. (CBSE Delhi 2015C)
|
Lens |
Power |
Aperture |
| L1 | 6 D | 1 cm |
| L2 | 3 D | 8 cm |
| L3 | 10 D | 1 cm |
Answer:
(a) For telescope
- Objective lens L2: Because it has a large focal length and large aperture
- Eye lens L3: Because it has a small focal length and small aperture
(b) For Microscope
- Objective lens L3: Because it has a small aperture and small focal length
- Eye lens L3: because it has a large aperture and large focal length
Question 22.
Draw a ray diagram to show how a right-angled isosceles prism may be used to bend the path of light by 90°.
Write the necessary condition in terms of the refractive index of the material of this prism for the ray to bend by 90°. (CBSE Delhi 2016C)
Answer:
The ray diagram is as shown.
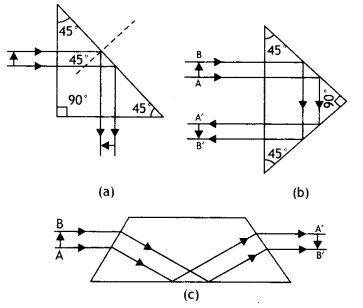
The angle of incidence in the denser medium should be greater than the critical angle for the given pair of media, i.e.
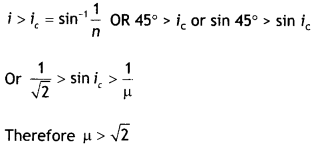
Question 23.
The image of a candle is formed by a convex lens on a screen. The lower half of the lens is painted black to make it completely opaque. Draw the ray diagram to show the image formation. How will this image be different from the one obtained when the lens is not painted black?
Answer:
The ray diagram depicting the image is shown
The image formed will be less bright as compared to that when half of the lens is not painted black. This is because every part of the lens forms the image. When the lower half is blackened, light from this portion will be blocked, hence the intensity of light in the image will be less.
Question 24.
A magician during a show makes a glass lens with n = 1.47 disappear in a trough of liquid. What is the refractive index of the liquid? Could the liquid be water?
Answer:
The refractive index of the liquid must be equal to 1.47 in order to make the lens disappear. This means n1 = n2. This gives 1 /f = 0 or f = ∞. The lens in the liquid will act as a plain sheet of glass. No, the liquid is not water, it could be glycerine.
Question 25.
Explain with reason, how the resolving power of an astronomical telescope will change, when
(a) frequency of the incident light on the objective lens is increased,
(b) the focal length of the objective lens is increased, and
(c) the aperture of the objective lens is halved?
Answer:
Resolving power of a telescope = \(\frac{D}{1.22 \lambda}\) hence
(a) on increasing the frequency of incident light, wavelength X decreases and consequently resolving power is increased.
(b) increase in focal length of the objective lens will have no effect on the resolving power, and
(c) if the aperture of the objective lens is halved, then resolving power is also halved.
Question 26.
Explain with reason, how the resolving power of a compound microscope will change when
(a) frequency of the incident light on the objective lens is increased,
(b) the focal length of the objective lens is increased, and
(c) the aperture of the objective lens is increased.
Answer:
Resolving power of a compound microscope RP = \(\frac{2 \mu \sin \theta}{\lambda}\), hence
(a) on increasing the frequency of incident light, its wavelength X decreases and consequently resolving power increases.
(b) on increasing the focal length of the objective lens, the value of sine and hence resolving power decreases.
(c) on increasing the aperture of the objective lens, the value of sin 0 and hence resolving power increases.
Question 27.
A convex lens of the focal length is kept in contact with a concave lens of focal length f2. Find the focal length of the combination. (CBSE AI 2013)
Answer:
For a convex lens +f1 and for a concave lens – f2, using the expression
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
or
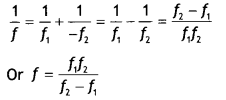
Question 28.
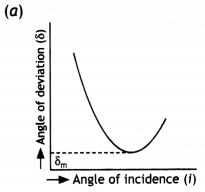
(a) The relation between the angle of incidence ‘i’ and the corresponding angle of deviation (δ), for a certain optical device, is represented by the graph shown in the figure. Identify this device. Draw a ray diagram for this device and use it for obtaining an expression for the refractive index of the material of this device in terms of an angle characteristic of the device and the angle, marked as δm, in the graph. (CBSE Al 2016C)
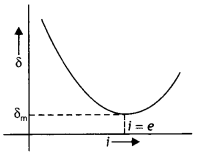
Answer:
(a) The device is a prism.
The relation is i + e = A + δm
In the minimum deviation position ∠i = ∠e
In the minimum deviation position we have A = r1 + r2 = r + r = 2r
or
r = A / 2
and i + i = A + δm
or
2i = A + δm
or
i = \(\frac{A+\delta_{m}}{2}\)
substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)
(b) The diagram is as shown.
Ray Optics and Optical Instruments Important Extra Questions Long Answer Type
Question 1.
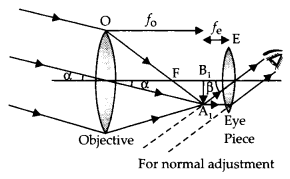
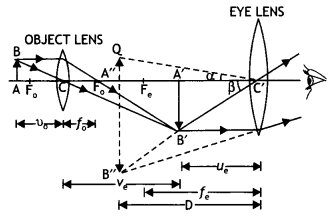
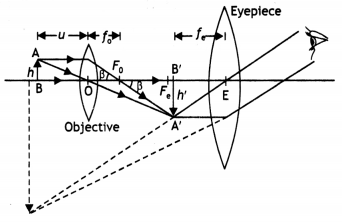
Draw a labelled ray diagram to show the image formation in a refracting type astronomical telescope. Obtain an expression for the angular magnifying power and the length of the tube of an astronomical telescope in its ‘normal adjustment’ position. Why should the diameter of the objective of a telescope be large?
Answer:
A labelled diagram of the telescope is shown in the figure.

The object subtends an angle at the objective and would subtend essentially the same angle at the unaided eye. Also, since the observers’ eye is placed just to the right of the focal point f’2, the angle subtended at the eye by the final image is very nearly equal to the angle β.
Therefore, M = \(\frac{\beta}{\alpha}=\frac{\tan \beta}{\tan \alpha}\) …(1)
From right triangles ABC and ABC’ as shown in figure, we have
tan α = \(\frac{\mathrm{AB}}{\mathrm{CB}}=\frac{-h}{f_{0}}\) and
tan β = \(\frac{\mathrm{AB}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{-h}{f_{\mathrm{e}}}\)
substituting the above two equations in equation (1), we have
M = \(\frac{\beta}{\alpha}=\frac{-h^{\prime}}{f_{e}} \times \frac{f_{0}}{-h^{\prime}}=\frac{f_{0}}{f_{e}}\)
The length of the telescope is the distance between the two lenses which is L = fo + fe The diameter of the objective of a telescope should be large so that it can collect more light and image of distant objects is formed clear.
Question 2.
Draw a ray diagram to show the formation of an erect image of an object kept in front of a concave mirror. Hence deduce the mirror formula. (CBSE 2019C)
Answer:
An object AB is placed between P and F. The course of rays for obtaining erect image A1B1 of object AB is shown in the figure.
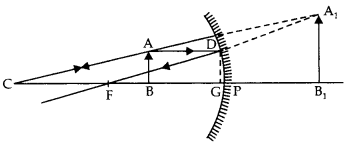
Draw DG ⊥ on the principal axis.
Triangles DGF and A1 B1C are similar

Since Point G is close to P, so GF = PF

Multiplying and dividing both sides by uvf, we get
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
Question 3.
(a) Define the term power of a lens. Write its SI units.
Answer:
The power of a lens is the reciprocal of its focal length in the metre.
i.e. P = \(\frac{1}{f(\text { in } m)}\)
S.I. unit of power of a lens is dioptre (D).
(b) Derive the expression for the power of two thin lenses placed coaxially in contact with each other. (CBSE 2019C)
Answer:
Power of two thin lenses in contact. Consider an object O placed at a distance u on the principal axis of the lens A. Rays of light starting from O forms, the image at I1
∴ \(\frac{1}{v_{1}}-\frac{1}{u}=\frac{1}{f_{1}}\) …(1)
Place lens B in contact with A. The image I1 will serve as a virtual object and forms a real image I.
∴ Again apply lens formula
\(-\frac{1}{v_{1}}+\frac{1}{v}=\frac{1}{f_{2}}\) …(2)
Adding (1) and (2), we have
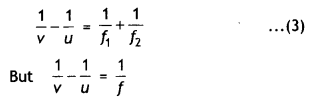
where f is the focal length of the combination
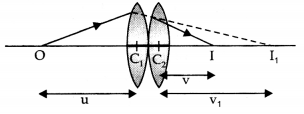
From (3), \(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
The total power of the lens combination is given by
P = P1 + P2
Question 4.
A biconvex lens of refractive index μ1 focal length ‘f and radius of curvature R is immersed in a liquid of refractive index μ2. For (i) μ2 > μ1, and (ii) μ2 < μ1, draw the ray diagrams in the two cases when a beam of light coming parallel to the principal axis is incident on the lens. Also, find the focal length of the lens in terms of the original focal length and the refractive index of the glass of the lens and that of the medium. (CBSE AI 2013C)
Answer:
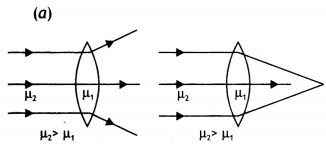
(b) Given: As the lens is equiconvex therefore R1 = R2 = R, aμg = μ1; aμ1 = μ2 fa = f, fL = ?
Using the expression
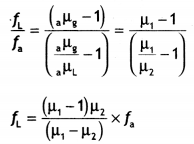
Question 5.
Write the conditions for observing a rainbow. Show, by drawing suitable diagrams, how one understands the formation of a rainbow. (CBSE AI 2014C)
Answer:
The conditions for observing a rainbow are that the sun should be shining in one part of the sky (say near the western horizon) while it is raining in the opposite part of the sky (say the eastern horizon). An observer can therefore see a rainbow only when his back is towards the sun.
Sunlight is first refracted as it enters a raindrop, which causes the different wavelengths (colours) of white light to separate. The longer wavelength of light (red) is bent the least while the shorter wavelength (violet) are bent the most. Next, these component rays strike the inner surface of the water drop and get internally reflected if the angle between the refracted ray and normal to the drop surface is greater than the critical angle (48°, in this case).
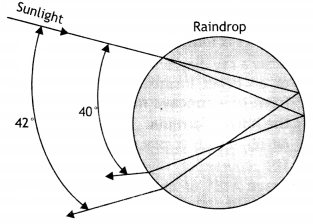
The reflected light is refracted again as it comes out of the drop as shown in the figure. It is found that the violet light, emerges at an angle of 40° related to the incoming sunlight and red light emerges at an angle of 42°. For other colours, angles lie in between these two values.
Question 6.
Explain the basic differences between the construction and working of a telescope and a microscope. (CBSE AI 2015)
Answer:
(a) In a telescope the objective has a large aperture and a large focal length, while in a microscope both the aperture and focal length of the objects are small (fe > fo). In a telescope, the eyepiece has a small aperture as compared to the objective, while in a microscope the eyepiece has a bigger aperture than the objective (fe < fo).
(b) A telescope increases the angle the object subtends at the eye thereby increasing its clarity by bringing it closer, while a microscope actually magnifies the object or a telescope magnifies distant objects, while a microscope magnifies nearby objects.
Question 7.
Why does white light disperse when passed through a glass prism?
Using the lens maker’s formula show how the focal length of a given lens depends upon the wavelength of light incident on it. (CBSE Delhi 2015C)
Answer:
It is because a glass prism offers a different refractive index to different wavelengths of light.
Lens maker’s formula is \(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\).
The refractive index depends upon wavelength as n ∝ \(\frac{1}{λ}\), therefore f ∝ λ.
Hence the focal length of a lens increases with the increase in the wavelength of light.
Question 8.
A thin converging lens has a focal length f in air. If it is completely immersed in a liquid, briefly explain, how the focal length of the lens will vary?
Answer:
The focal length of a converging lens is given by
\(\frac{1}{f}\) = (ang – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
where ang = refractive index of Lens with respect to air.
And In a given liquid medium the focal Length of the Lens is given by
\(\frac{1}{f_{m}}\) = (mng – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
Therefore the ratio of the totaL focal Length is
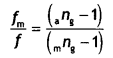
(a) If mng < ang then f is +ve and has a value greater than f, i.e. focal length of the lens increases when immersed in a given liquid medium.
(b) If mng >ang, then f is -ve, i.e. the lens will begin to behave as a diverging lens.
Question 9.
When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency. Explain why?
Answer:
Reflection and refraction arise through the interaction of incident light with the atomic constituents of matter. Atoms may be viewed as oscillators that take up the frequency of the external agency (light) causing forced oscillations. The frequency of light emitted by a charged oscillator equals its frequency of oscillation. Thus the frequency of scattered light equals the frequency of incident light.
Question 10.
The image of an object formed by the combination of a convex lens (of focal length f) and a convex mirror (of the radius of curvature R), set up as shown is observed to coincide with the object. Redraw this diagram to mark on it the position of the centre of curvature of the mirror. Obtain the expression for R in terms of the distances marked as ‘a’ and ‘d’ and focal length f of the convex lens. (CBSE Delhi 2016C)
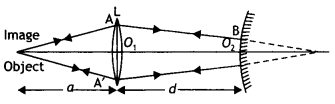
Answer:
The final image, formed by the combination, is coinciding with the object itself. This implies that the rays, from the object, are retracing their path, after refraction from the tens and reflection from the mirror. The (refracted) rays are, therefore, fatling normally on the mirror. It follows that the rays A B, and A’ B’, when produced, are meeting at the centre of curvature C of the mirror. Hence C is the centre of curvature of the mirror.
From the figure, we then see that for the convex lens we have
u = – a and v = + (d + R). If f is the focal length of the lens, we have
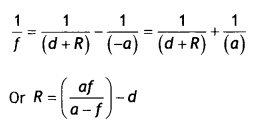
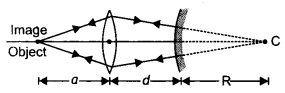
Question 11.
Define the magnifying power of a compound microscope when the final image is formed at infinity. Why must both the objective and the eyepiece of a compound microscope have short focal lengths? Explain. (CBSE Delhi 2017)
Answer:
It is defined as the ratio of the angle subtended on the eye by the final image when it lies at infinity to the angle subtended on the eye by the object when it lies at the least distance of distinct vision from the eye or the near point of the eye. The magnifying power of a microscope is given by
M = Me × Mo = \(\frac{L}{f_{0}} \times\left(1+\frac{D}{f_{e}}\right)\)
Since it depends inversely on the focal lengths of the objective and the eyepiece, therefore both have to be small to get a large magnification.
Question 12.
(a) Draw a ray diagram for the formation of the image by a compound microscope.
Answer:
The ray diagram is as shown.
(b) You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct a compound microscope?
| Lenses | Power(D) |
Aperture(cm) |
| L1 | 3 | 8 |
| L2 | 6 | 1 |
| L3 | 10 | 1 |
Answer:
The objective should have a short focal length and large aperture while the eyepiece should have a short focal length and small aperture. Thus for objective lens L3 should be used and for eyepiece lens, L2 should be used.
(c) Define the resolving power of a microscope and write one factor on which it depends. (CBSE AI 2017)
Answer:
The resolving power of a microscope is given by the expression
RP = \(\frac{2 \mu \sin \theta}{1.22 \lambda}=\frac{2 \mu v \sin \theta}{1.22 c}\)
It depends upon the wavelength/ frequency of the incident light.
Question 13.
Draw a labelled ray diagram of an astronomical telescope in the near point adjustment position. (CBSE Delhi 2019)
A giant refracting telescope at an observatory has an objective lens of focal length 15 m and an eyepiece of focal length 1.0 cm. If this telescope is used to view the Moon, find the diameter of the image of the Moon formed by the objective lens. The diameter of the Moon is 3.48 × 106 m, and the radius of the lunar orbit is 3.8 × 108 m.
Answer:
A Labelled ray diagram is as shown.
Given fo = 15 m, fe = 1.0 cm = 0.01 m, M = ? Dm = 3.48 × 106 m, r = 3.8 × 108 m,
Using M = \(\frac{f_{0}}{f_{e}}=\frac{15}{0.01}\) = 1500
The angle subtended by the moon at the objective of the telescope

Question 14.
(a) Amobilephoneliesalongtheprincipal axis of a concave mirror. Show with the help of a suitable diagram the formation of its image. Explain why magnification is not uniform.
Answer:
The image of the mobile phone formed by the concave mirror is shown in the below figure.
The part of the mobile phone that is at C will form an image of the same size only at C. In the figure, we can see that B’C = BC. The part of the mobile phone that lies between C and F will form an enlarged image beyond C as shown in the figure. It can be observed that the magnification of each part of the mobile phone cannot be uniform on account of different locations. That is why the image formed is not uniform.
(b) Suppose the lower half of the concave mirrors reflecting surface is covered with an opaque material. What effect this will have on the image of the object. Explain. (CBSE Delhi 2014)
Answer:
The intensity of the image will decrease while the whole image will be for.
Question 15.
(a) Draw a labelled ray diagram of a compound microscope, when the final image forms at the least distance of distinct vision.
(b) Why is its objective of short focal length and of short aperture compared to its eyepiece? Explain.
(c) The focal length of the objective is 4 cm while that of the eyepiece is 10 cm. The object is placed at a distance of 6 cm from the objective lens.
(i) Calculate the magnifying power of the compound microscope, if its final image is formed at the near point.
(ii) Also calculate the length of the compound microscope. (CBSE AI 2019)
Or
(a) With the help of a labelled ray diagram, explain the construction and working of a Cassegrain reflecting telescope.
(b) An amateur astronomer wishes to estimate roughly the size of the sun using his crude telescope consisting of an objective lens of focal length 200 cm and an eyepiece of focal length 10 cm. By adjusting the distance of the eyepiece from the objective, he obtains an image of the sun on a screen 40 cm behind the eyepiece. The diameter of the sun’s image is measured to be 6-0 cm. Estimate the sun’s size, given that the average earth-sun distance is 1.5 × 1011 m.
Answer:
(a) The diagram is as shown.
(b) The magnifying power of compound microscope m = m0 × me = \(\frac{L}{f_{o}}\left(1+\frac{D}{f_{e}}\right)\)
To have high magnifying power and high resolution, the focal length of the objective and its aperture should be short.
The focal length of the eyepiece is comparatively greater than the objective so an image formed by the objective lens may form within the focal length of the eyepiece and the final magnified image may be formed.
Aperture is short for higher resolution,
(c) Given uo = – 6 cm
For objective lens we have

(i) For magnifying power of compound microscope we have
m = \(\frac{v_{o}}{u_{o}}\left(1+\frac{D}{f_{e}}\right)=\frac{12}{6}\left(1+\frac{25}{10}\right)\) = 7
(ii) Length of the compound microscope L = v0 + ue = 12 + 7.14 = 19.14 cm
Or
(a) Cassegrain reflecting telescope consists of a large concave (primary) parabolic mirror having a hole in its centre. There is a small convex (secondary) mirror near the focus of the concave mirror. The eyepiece is placed near the hole of the concave mirror. The parallel rays from a distant object are reflected by the large concave mirror. These rays fall on the convex mirror which reflects these rays outside the hole. The final magnified image is formed at infinity.
The diagram is as shown.
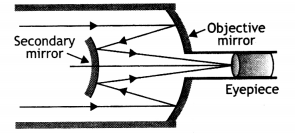
(b)
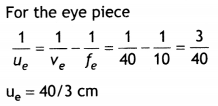
Magnification produced by the eye piece is
me = \(\frac{v_{e}}{u_{e}}=\frac{40}{40 / 3}\) = 3
Diameter of the image formed by the objective is
D = 6/3 = 2 cm
If D is the diameter of the sun then the angle subtended by it on the objective will be
α = \(\frac{D}{1.5 \times 10^{11}}\) rad
Now, angle subtended by the image at the objective = angle subtended by the sun
α = \(\frac{\text { size of image }}{f_{0}}=\frac{2}{200}=\frac{1}{100}\) rad
Therefore,
\(\frac{D}{1.5 \times 10^{11}}=\frac{1}{100}\)
D = 1.5 × 109
Question 16.
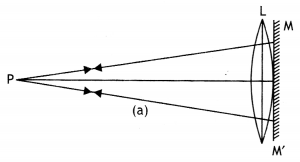
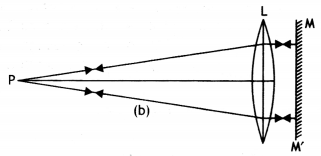
A convex lens is placed in contact with a plane mirror. An axial point object, at a distance of 20 cm from this combination, has its image coinciding with itself. What is the focal length of the convex lens?
Answer:
Figure (a) shows a convex lens L in contact with a plane mirror M. P is the point object, kept in front of this combination at a distance of 20 cm, from it. Since the image of the object is coinciding with the object itself, the rays from the object, after refraction from the lens, should fall normally on the mirror M, so that they retrace their path and form an image coinciding with the object itself.
This will be so, if the incident rays from P form a parallel beam perpendicular to M, after refraction from the lens. For clarity, M has been shown at a finite distance from L, in figure (b). For lens L, since the rays from P form a parallel beam after refraction, P must be at the focus of the lens. Hence the focal length of the lens is 20 cm.
Question 17.
A convex lens and a convex mirror (of the radius of curvature 20 cm) are placed co-axially with the convex mirror placed at a distance of 30 cm from the lens. For a point object, at a distance of 25 cm from the lens, the final image, due to this combination, coincides with the object itself. What is the focal length of the convex lens?
Answer:
The ray diagram is as shown.
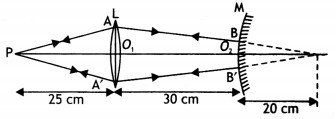
The final image, formed by the combination, is coinciding with the object itself. This implies that the rays, from the object, are retracing their path, after refraction from the lens and reflection from the mirror. The (refracted) rays are, therefore, falling normally on the mirror. It follows that the rays A B, and A’ B’, when produced, are meeting at the centre of curvature C of the mirror. Hence O2C = 20 cm, the radius of curvature of the mirror. From the figure, we then see that for the convex lens u = – 25 cm and v = + (30 + 20) cm = + 50 cm. If f is the focal length of the lens, we have
\(\frac{1}{50}-\frac{1}{(-25)}=\frac{1}{f}\)
or
f = 16.67 cm
Question 18.
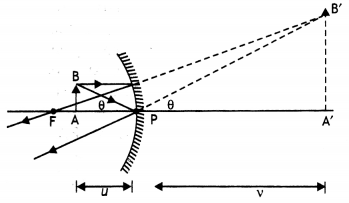
Derive a relation between focal length, image distance and object distance for a
concave mirror.
Answer:
Consider a concave mirror of small aperture, image distance and object distance for a Figure below shows two rays of light leaving the tip of the object. One of these rays passes through the centre of curvature C of the mirror, hitting the mirror head-on and reflecting back on itself. The second ray BP strikes the mirror at its pole P and reflects as shown obeying the laws of reflection. The image of the tip of the arrow is located at the point where these two rays intersect. Thus the image is formed between the focus and centre of curvature.
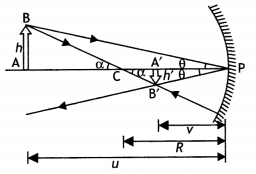
Consider the two right-angled triangles BAP and B’A’P
Now from triangle BAP using trigonometry, we have
tan θ = \(\frac{AB}{PA}\) …(1)

Therefore equation (7) becomes
\(\frac{\mathrm{PA}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PA}-\mathrm{PC}}{\mathrm{PC}-\mathrm{PA}^{\prime}}\)
By Cartesian sign conventions we have PA = -u, PA’ = -v and PC = – R, substituting in equation (8), we have
simplifying we have 2uv = vR + uR dividing both sides by uvR we have
\(\frac{1}{u}+\frac{1}{v}=\frac{2}{R}\) …(11)
but R = 2 f, where f is the focal length of the mirror. Therefore the above equation
reduces to \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
which is the required mirror formula.
Question 19.
With the help of a suitable ray diagram, derive a relation between the object distance (u) image distance v and radius of curvature (R) for a convex spherical surface, when a ray of light travels from rarer to denser medium. (CBSE Delhi 2011C)
Answer:
Let a convex spherical surface XPY separate a rarer medium of refractive index (n<sub>1</sub>) from a denser medium of refractive (n2). The real image of object 0 is formed by refraction from the convex spherical surface of radius of curvature R. The angle α β γ are shown in the figure.
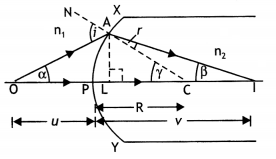
Let ∠AOP = α, ∠AIP = β and ∠ACP = γ.
From point A, drop AN perpendicular to the principal axis of the spherical refracting surface. From triangle AOC, we have
i = α + γ
Since the aperture of the spherical refracting surface is small, point A will be close to point P and hence angles α, β and γ will be small. As such, these angles may be replaced by their tangents.
Therefore, equation (1) may be written as
i = tanα + tanγ …(2)
From right angled triangles ΔALO and ΔALC, we have
tan α = \(\frac{AL}{LO}\) and tan γ = \(\frac{AL}{LC}\)
Substituting for tan α and tan γ in equation (2), we have
i = \(\frac{AL}{LO}\) + \(\frac{AL}{LC}\) …(3)
Again, as aperture of the refracting surface is small, point L will be close to point P, the pole of the refracting surface.
Therefore,
LO ≈ PO and LC ≈ PC
Therefore, equation (3) becomes
i = \(\frac{AL}{PO}\) + \(\frac{AL}{PC}\) …(4)
Now, from triangle ΔACI, γ = r + β
or
r = γ— β
Since angles γ and β are small, we have
r = tan γ— tan β …(5)
From right angled triangles ΔALC and ΔALI,
we have
tan γ = \(\frac{A L}{L C} \approx \frac{A L}{P C}\) and tan β = \(\frac{A L}{L I} \approx \frac{A L}{P I}\)
Substituting for tan β and tan γ in equation (5) we have
r = \(\frac{\mathrm{AL}}{\mathrm{PC}}-\frac{\mathrm{AL}}{\mathrm{PI}}\) …(6)
Now by Snell’s Law at point A we have
n1 sin i = n2 sin r
Since angles are small, therefore the above relation becomes
n1 i = n2 r …(7)
Substituting the values of i and r from equations (4) and (6) we have
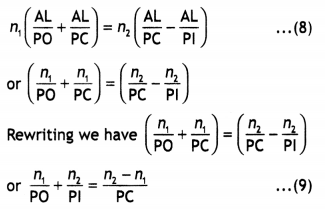
Applying new Cartesian sign conventions:
PO = – u (a distance of the object is against incident Light)
PI = + v (distance of image Is along incident Light)
PC = + R (a distance of the centre of curvature is along with incident Light) we have
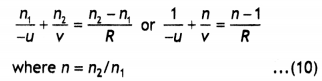
The above equation connects u, V and R to the absolute refractive indices of the material of the refracting surface and that of the rarer medium.
Question 20.
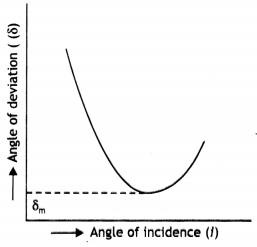
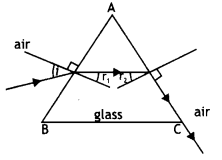
A ray of light Is an Incident on one face of a glass prism and emerges out from the other face. Trace the path of the ray and derive an expression for the refractive index of the glass prism. Also, plot a graph between the Angle of incidence and angle of deviation. (CBSE Delhi 201 IC)
Answer:
The graph is as shown
Consider a cross-section XYZ of a prism as shown in the figure. Let A be the angle of the prism. A ray PQ of monochromatic light is incident on face XY of the prism at an angle i. The ray is called the incident ray and the angle is called the angle of incidence. This ray is refracted towards the normal NQE and travels in the prism along QR. This ray is called the refracted ray at the face XY.
Let r1 be the angle of refraction at this surface. The refracted ray QR is incident at an angle r2 on the surface XZ. The ray QR again suffers refraction and emerges out of face XZ at an angle e along with RS. The ray is called the emergent ray and the angle e is called the angle of emergence. When the ray SR is extended backwards it meets the extended ray PQ at point D such that δ is the angle of deviation of the ray.
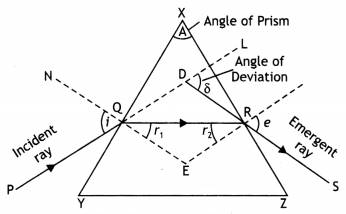
As seen from figure we have in triangle QDR that ∠DQR = i – r1 and
∠DRQ = e – r2. Therefore from triangle QDR we have
δ = ∠DQR + ∠DRQ = (i – r1) + (e – r2)
or
δ = (i + e) – (r1 + r2) …(1)
Now from the quadrilateral XQER, we have
A + E = 180° …(2)
In triangle QER we have r1 + r2 + e – 180° …(3)
From equations (2) and (3) we have
A = r1 + r2 …(4)
Substituting in equation (1) we have
δ = i + e – A
or
i + e = A + δ … (5)
The deviation produced by a prism depends upon (i) the angle of incidence (ii) the angle of prism and (Hi) the refractive index of the material of the prism. It is found that as the angle of incidence changes, the angle of deviation also changes.
A graph between the angle of incidence and the angle of deviation is shown in the figure above. As the angle of incidence increases, the angle of deviation first decreases becomes a minimum for a particular angle of incidence and then increases. The minimum value of the angle of deviation is called the angle of minimum deviation. It is denoted by δm. In this position the ray of light passes symmetrically through the prism, i.e. the refracted ray QR is parallel to the base of the prism. In this position, the angle of incidence is equal to the angle of emergence, i.e. i = e. Also in this position, the angle of refraction at the faces of the prism are equal, i.e. r1 = r2.
Substituting these values in equations (4) and (5) we have
A = r1 + r2 = r + r = 2r
or
r = A/2 …(6)
and i + i = A + δm
or
2i = A + δm
or
i = \(\frac{A+\delta_{m}}{2}\) …(7)
substituting for i and r in the expression for Snell’s law we have
μ = \(\frac{\sin i}{\sin r}=\frac{\sin \left[\frac{A+\delta_{m}}{2}\right]}{\sin \left(\frac{A}{2}\right)}\)
Question 21.
(a) Draw a ray diagram showing the image formation by a compound microscope. Obtain an expression for total magnification when the image is formed at infinity.
Answer:
The ray diagram is as shown.
(b) How does the resolving power of a compound microscope get affected, when
(i) the focal length of the objective is decreased.
(ii) the wavelength of light is increased? Give reasons to justify your answer. (CBSE AI 2015C)
Answer:
The resolving power of a microscope is given by the expression RP = \(\frac{2 n \sin \theta}{\lambda}\)
(i) There is no effect of the increase in the focal length of the objective on the resolving power of the microscope.
(ii) If the wavelength of the incident light is increased, the resolving power of the microscope also decreases.
Question 22.
An optical instrument uses eye-lens of power 12.5 0 and an object lens of power 50 D and has a tube length of 20 cm. Name the optical instrument and calculate its magnifying power, if it forms the final image at infinity. (CBSE Delhi 2017C)
Answer:
It is a compound microscope.
The ray diagram is as shown.
Let mo and me be the magnifications produced by the objective lens and eye lens respectively, the total magnifying power of the microscope
M = mo x me
Now mo = – \(\frac{v_{0}}{u_{0}}\)
Also, the magnifying power of the eyepiece when the final image is formed at infinity
me = \(\frac{D}{f_{e}}\)
Thus magnifying power of the microscope is
M = \(\frac{-v_{0}}{u_{0}} \times \frac{D}{f_{e}}\)
As a first approximation, ue ≈ fe and ve ≈ L = distance between objective and eyepiece (or length of microscope tube), then we have
M = \(\frac{-L}{f_{0}} \times \frac{D}{f_{e}}\)
Question 23.
Use the mirror equation to show that
(i) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Answer:
By mirror formula we have \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Therefore \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) and for concave mirror u and f both are having negative sign, i.e. f < 0 and u < 0.
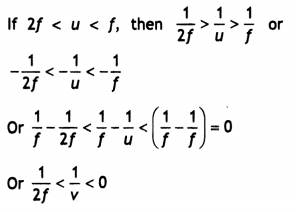
It means that v > 2f, having a negative sign. Thus, the image is real and lies beyond 2f.
(ii) a convex mirror always produces a virtual image independent of the location of the object.
Answer:
(Ii) For a convex mirror \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) but f is positive and u is negative, i.e. f >0 but u < 0.
Therefore, it is self-evident from the above relation that irrespective of the value of u, the value of v is aLways +ve. It means that the Imaged formed by the convex mirror is always virtual independent of the location of the object.
(iii) an object placed between the pole and the focus of a concave mirror produces a virtual and enlarged image. (CBSE AI 2011)
Answer:
As for a concave mirror f and u, both are negative, hence
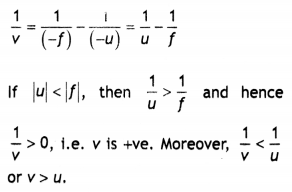
It means that for an object placed between the pole and principal focus of a concave mirror the image formed (as v is +ve) is virtual and magnification
m = \(\frac{1}{O}=\frac{|v|}{|u|}\) > 1, i.e. the image is an enlarged image.
Question 24.
(i) Obtain Lens makers formula using the expression \(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{\left(n_{2}-n_{1}\right)}{R}\), here the ray of light propagating from a rarer medium of refractive index (n1) to a denser medium of refractive index (n2) is incident on the convex side of spherical refracting surface of radius of curvature R.
(ii) Draw a ray diagram to show the image formation by a concave mirror when the object is kept between its focus and the pole. Using this diagram, derive the magnification formula for the Image formed. (CBSE DelhI 2011)
Answer:
(i) The course of rays through the Lens Is as shown. For refraction at the spherical surface XP1Y, we have
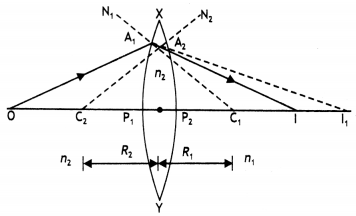
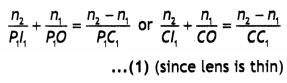
Consider the second surface XP2Y. Actually, the materiaL of the Lens does not extend beyond XP1Y. Therefore, before the refracted ray from A1 could meet the principal axis, it will suffer refraction at point A2 on the second face XP2Y and the Lightray will finally meet the principal axial. Such that l is the final image. Thus point lies the real Image of the virtual object I. Hence for refraction at the surface XP2Y we have

The above equation becomes
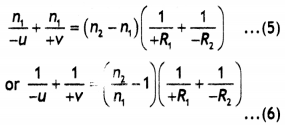
But n2/n1 = n, the absolute refractive index of the material of the lens, therefore the above equation takes the form
\(\frac{1}{v}-\frac{1}{u}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
But by lens formula we have \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
Therefore, from the above two equations we have
\(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) …(7)
This is the Lens maker’s equation or formula.
(ii) The ray diagram is as shown
Now from triangle BAP we have
tan θ = \(\frac{AB}{PA}\) …(1)
Also from triangle B’A’P, we have A’B’
tan θ = \(\frac{A^{\prime} B^{\prime}}{P A^{\prime}}\) …(2)
Comparing equations (1) and (2), we have
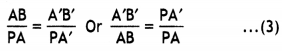
By Cartesian sign convention AB = h, A’B’ = h’, PA = – u and PA’= v . Substituting in equations (3) we have
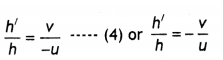
But \(\frac{h^{\prime}}{h}\) = m ( Linear magnification),
therefore
m = – \(\frac{\text { image distance }}{\text { object distance }}\)
Question 25.
(a) Two thin convex lenses L1 and L2 of focal lengths f1 and f2 respectively, are placed coaxially in contact. An object is placed at a point beyond the focus of lens L1. Draw a ray diagram to show the image formation by the combination and hence derive the expression for the focal length of the combined system.
Answer:
Consider two lenses A and B of focal length f1 and f2 placed in contact with each other. Let the object be placed at a point O beyond the focus of the first lens L1 as shown.
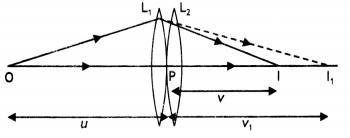
The first lens L1 produces an image at l1 Since image l2 is real, it serves as a virtual object for the second lens L2, producing the final image at l. Since the lenses are thin, we assume the optical centres of the lenses to be coincident. Let this central point be denoted by P.
For the image formed by the first lens L1, we get
\(\frac{1}{v_{1}}-\frac{1}{u}=\frac{1}{f_{1}}\) …(i)
For the image formed by the second lens L2, we get
\(\frac{1}{v}-\frac{1}{v_{1}}=\frac{1}{f_{2}}\) …(ii)
Adding equations (i) and (ii) we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\) …(iii)
If the two lens-system is regarded as equivalent to a single lens of focal length f, we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) …(iv)
Therefore from equations (iii) and (iv) we get
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
(b) A ray PQ incident on the face AB of a prism ABC, as shown in the figure, emerges from the face AC such that AQ = AR.
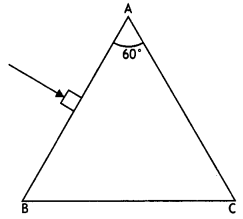
Draw the ray diagram showing the passage of the ray through the prism. If the angle of the prism is 60° and the refractive index of the material of the prism is \(\sqrt{3}\), determine the values of angle of incidence and angle of deviation. (CBSE AI 2015)
Answer:
The ray diagram is as shown
The prism, in this situation, is in the minimum deviation position, therefore we have
r = \(\frac{A}{2}=\frac{60}{2}\) = 30°
Hence n = \(\frac{\sin i}{\sin r}=\frac{\sin i}{\sin 30^{\circ}}\) = \(\sqrt{3}\)
This gives, i = 60°
Hence from
i = \(\frac{A+\delta_{m}}{2}\) we have
δm = 2i – A = 2 × 60° – 60° = 60°
Question 26.
(a) Plot a graph to show the variation of the angle of deviation as a function of the angle of incidence for light passing through a prism. Derive an expression for the refractive index of the prism in terms of angle of minimum deviation and angle of prism.
(b) What is the dispersion of light? What is its cause?
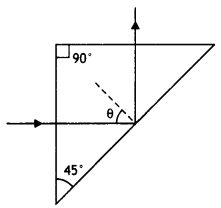
(c) A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in the figure. What must be the minimum value of the refractive index of glass? Give relevant calculations. (CBSE Delhi 2016)
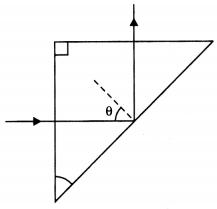
Answer:
For a prism we have
i + e = A + δ …(1)
From the graph between the angle of incidence and the angle of deviation it follows that as the angle of incidence increases, the angle of deviation first decreases becomes a minimum for a particular angle of incidence and then again increases. The minimum value of the angle of deviation is called the angle of minimum deviation. It is denoted by 5m. In this position the ray of light passes symmetrically through the prism, i.e. the refracted ray QR is parallel to the base of. the prism. In this position, the angle of incidence is equal to the angle of emergence, i.e. i = e. Also in this position, the angle of refraction at the faces of the prism are equal, i.e. r1 = r2. Substituting these values in equations (4) and (5) we have
A = r1 + r2 = r + r = 2r
or
r = A/2 …(2)
and
i + i = A + δm
or
2i = A + δm
or
i = \(\frac{A+\delta_{m}}{2}\) …(3)
Substituting for i and r in the expression for Snell’s law we have a speed of light in a vacuum
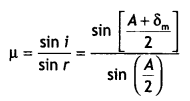
(b) The phenomenon of splitting a ray of white tight into its constituent colours (wavelengths) is catted dispersion.
Cause: It is because different wavelengths travel at different speeds In a medium other than vacuum.
(C) The diagram of the path of rays through the prism is as shown.
Here θ = 45° > ic
Now n = \(\frac{1}{\sin i_{c}}=\frac{1}{\sin 45^{\circ}}=\frac{1}{1 / \sqrt{2}}=\sqrt{2}\)
Therefore n > \(\sqrt{2}\)
Numerical Problems :
Formulae for solving numerical problems
- When Light travels from an optically denser medium to an optically rarer medium It bends away from the normal.
- When light travels from an optically rarer medium to an optically denser medium It bends towards from the normal. speed of Light in vacuum
- μ = \(\frac{\text { speed of light in vacuum }}{\text { speed of light in the medium }}\)
- μ = \(\frac{1}{\sin \theta_{c}}\)
- In minimum deviation position A = 2r or
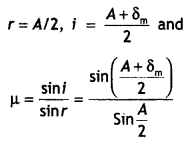
- Lens maker’s formula
\(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) - MagnifyIng power of a compound microscope
M = Me × Mo = \(\frac{L}{f_{0}} \times\left(1+\frac{D}{f_{e}}\right)\)
Question 1.
A convex lens made up of a glass of refractive index 1.5 is dipped, In turn, In
(a) a medium of refractive index 1.65,
Answer:
When dipped in the medium of refractive index 1.65, it will behave as a concave lens and when dipped in the medium of refractive index 1.33, it will behave as a convex lens.
(b) a medium of refractive index 1.33.
(i) Will it behave as a converging or a diverging lens in the two cases?
Answer:
Its focal length in another medium is given by
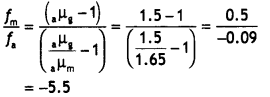
Thus fm = -5.5 fa, i.e. focal length increases and becomes negative.
(ii) How will Its focal length change In the two media? (CBSE AI 2011)
Answer:
Similarly
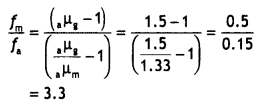
Thus fm = 3.3 fa, i.e. focal length increases.
Question 2.
A compound microscope uses an objective lens of focal length 4 cm and an eyepiece lens of focal length 10 cm. An object is placed at 6 cm from the objective lens. Calculate the magnifying power of the compound microscope. Also, calculate the length of the microscope. (CBSE Al 2011)
Answer:
fo = 4 cm, fe = 10 cm, uo = – 6 cm, M = ?, L = ?
Using
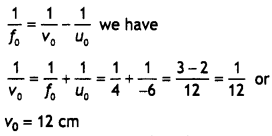
Hence angular magnification
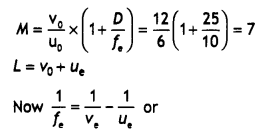
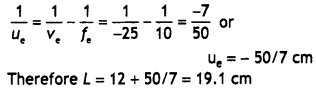
Question 3.
A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece lens of focal length 1 cm is used, find the angular magnification of the telescope.
If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.42 × 106 m and the radius of the lunar orbit is 3.8 × 108 m. (CBSE AI 2011, Delhi 2015)
Answer:
Given fo = 15 m, fe = 1.0 cm = 0.01 m, M = ?
Dm = 3.48 × 106 m, r = 3.8 × 108 m,
Using M = \(\frac{f_{0}}{f_{\mathrm{e}}}=\frac{15}{0.01}\) = 1500
The angle subtended by the moon at the objective of the telescope

Question 4.
A beam of light converges at a point P. A concave lens of focal length 16 cm is placed in the path of this beam 12 cm from P. Draw a ray diagram and find the location of the point at which the beam would now converge. (CBSE Delhi 2011C)
Answer:
The ray diagram is shown in the figure. In the absence of the concave lens the beam converges at point P. When the concave lens is introduced, the incident beam of light is diverged and now comes to focus at point Q. Thus for the concave lens P serves as a virtual object giving rise to a real Image at Q.
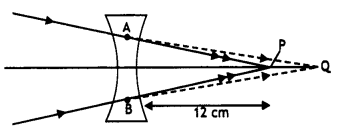
Here u = + 12 cm, f = – 16 cm, v = ?, Now for a lens
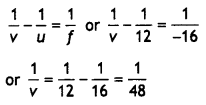
Hence v = 48 cm
i. e. the point at which the beam is focused is 48 cm from the lens.
Question 5.
Two convex lenses of focal length 20 cm and 1 cm constitute a telescope. The telescope is focused on a point that is 1 m away from the objective. Calculate the magnification produced and the length of the tube, if the final image Is formed at a distance of 25 cm from the eyepiece. (CBSE Delhi 2011 C)
Answer:
Given fo = 2o cm, fe = 1 cm, u = – 100 cm, M =?, y =?
Fora lens \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
or
\(\frac{1}{v}-\frac{1}{-100}=\frac{1}{20}\)
or
v = 25cm
Since the eye lens forms the image of the virtual object at the distance of distinct vision for the eye lens
v = – 25 cm, fe = 1 cm,
Now \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
or
\(\frac{1}{-25}-\frac{1}{u}\) = 1
or
u = – \(\frac{25}{26}\)cm
Now magnification produced by the object lens
mo = \(\frac{v}{u}=-\frac{25}{100}=-\frac{1}{4}\)
Magnification produced by the eye Lens
me = \(\frac{v}{u}=\frac{-25}{-25}\) × 26 = 26
Hence total magnification
M = mo × me = -1 /4 × 26 = – 6.5
Question 6.
(a) Under what conditions are the phenomenon of total internal reflection of light observed? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
(b) Three lenses of focal lengths +10 cm, -10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination. (CBSE Delhi 2019 C)
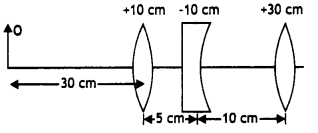
Answer:
(a) (i) Light travels from a denser medium to a rarer medium.
(ii) Angle of Incidence in the denser medium is more than the critical angle for a given pair of media.
For the grazing incidence n sin iC = l sin 90°
n = \(\frac{1}{\sin i_{c}}\)
(b) For convex lens f = + 10 cm
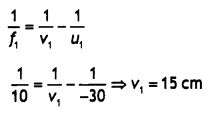
Object distance for concave lens u2 = 15 – 5 = 10 cm
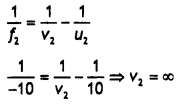
For third lens
\(\frac{1}{f_{3}}=\frac{1}{v_{3}}-\frac{1}{\infty}\) ⇒ v3 = 30 cm
Question 7.
A ray of light incident on an equilateral glass prism (μg = \(\sqrt{3}\)) moves parallel to the baseline of the prism inside it. Find the angle of Incidence for this ray. (CBSE Delhi 2012)
Answer:
Given A = 60°, μg = \(\sqrt{3}\), i = ?
Using the expression μ = \(\frac{\sin i}{\sin A / 2}\)
or
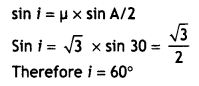
Question 8.
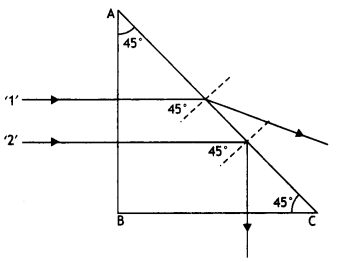
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays ‘1’ and ‘2’ are respectively 1.35 and 1.45. Trace the path of these rays after entering through the prism. (CBSE AI 2014)
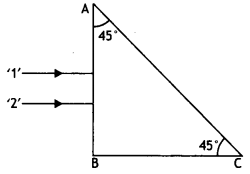
Answer:
The critical angle for the two rays is
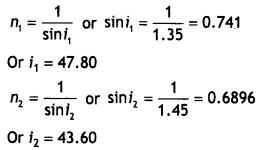
This shows that the angle of Incidence for ray ‘2’ Is greater than the critical angle. Hence it suffers total internal reflection, white ray ‘1’ does not. Hence the path of rays is as shown.
Question 9.
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept at 15 cm from each other. A point object lies 60 cm in front of the convex lens. Draw a ray diagram to show the formation of the image by the combination. Determine the nature and position of the image formed. (CBSE AI 2014)
Answer:
The ray diagram is as shown.
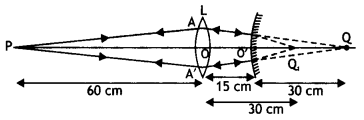
For the convex lens, we have
u1 = – 60 cm, f = + 20 cm, v = ?
Using lens formula we have
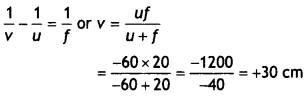
Had there been only the Lens, the image would have been formed at Q1, which acts as a virtual object for the convex mirror.
Therefore u2 = OQ1 – OO’ = 30 – 15 = 15 cm
Using mirror formuLa we have
\(\frac{1}{v_{2}}+\frac{1}{u_{2}}=\frac{2}{R}\)
or
\(\frac{1}{v_{2}}+\frac{1}{u_{15}}=\frac{2}{20}\)
Solving for v2 we have
v2 = 30cm
Hence the final image is formed at (Point Q) a distance of 30 cm behind the mirror.
Question 10.
A ray PQ is an incident normally on the face AB of a triangular prism refracting angle of 60°, made of a transparent material of refractive index 2 / \(\sqrt{3}\), as shown in the figure. Trace the path of the ray as it passes through the prism. Also, calculate the angle of emergence and angle deviation. (CBSE Delhi 2014C)
Answer:
Critical angle for glass
µ = \(\frac{1}{\sin i_{c}}\)
or
sin ic = \(\frac{1}{\mu}=\frac{\sqrt{3}}{2}\)= 0.866
or
ic = 60°
Now the ray is incident at an angle of 60° which is equal to the critical angle, therefore the ray graces the other edge of the prism
Therefore the angle of emergence is = 90°
Hence δ = 30°
This is as shown.
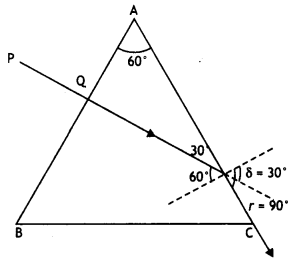
Question 11.
An object Is placed 15 cm In front of a convex lens of focal length 10 cm. Find the nature and position of the image formed. Where should a concave mirror of radius of curvature 20 cm be placed so that the final image is formed at the position of the object itself? (CBSE AI 2015)
Answer:
Given u = -15 cm, f = + 10 cm, v = ?
For lens we have
Nature of image-real, magnified Final image formed will be at the object itself only if the image formed by the lens is at the position of the centre of curvature of the mirror
∴ Distance of mirror from lens, D = 30 + R = 30 + 20 cm = 50 cm
Question 12.
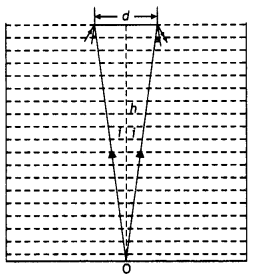
Define the critical angle for a pair of media. A point source of monochromatic light ‘S’ is kept at the centre of the bottom of a cylinder with the radius of 15 cm. The cylinder contains water (refractive index 4/3) to a height of 7.0 cm. Draw the ray diagram and calculate the area of the water surface through which the light emerges in the air. (CBSE Delhi 2015C)
Answer:
It the angle of incidence in the denser medium for which the angle of refraction in the rare medium is 90°.
Given h = 7 cm, A = πr² = ?, μ = 4/3 = 1.33
Due to total internal reflection light from the bulb will not come out of the entire surface of the water as shown.
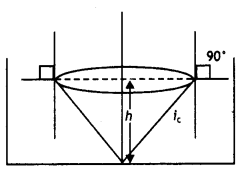
The angle of the cone through which tight will spread out is twice the critical angle.
Therefore the radius of the circular patch will be
Using the relation r= \(\frac{h}{\sqrt{\mu^{2}-1}}\) we have
r = \(\frac{7}{\sqrt{(1.33)^{2}-1}}\) = 7.98 cm
Therefore area of the surface of water through which light comes out
A = πr² = 3.14 × (7.98)² = 199.95 cm²
Question 13.
A ray PQ incident on the refracting face BA Is refracted in the prism BAC as shown In the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive Index of the material of prism is \(\sqrt{3}\), calculate angle θ. (CBSE AI 2016)
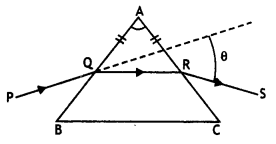
Answer:
Here As AQ = AR, therefore QR is parallel to BC, hence prism is in minimum deviation position
A = 60°, θ = δm = ?, n = \(\sqrt{3}\)
Solving θ = 60°
Question 14.
(i) A ray of light incident on face AB of an equilateral glass prism shows a minimum deviation of 30°. Calculate the speed of light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along with the face AC. (CBSE Delhi 2017)
Answer:
(i) Given
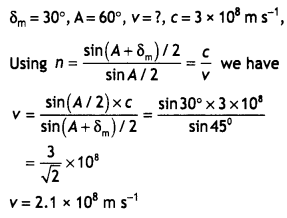
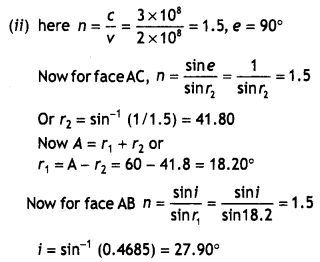
Question 15.
A small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index p up to a height h. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut off light from the bulb. (CBSE Sample Paper 2018-19)
Answer:
Let d be the diameter of the disc. The bulb shall be invisible if the incident rays from the bulb at 0 to the surface at d/2 are at the critical angle.
Let l be the angle of incidence
Then sin i = \(\frac{1}{μ}\) = tan i.
Now
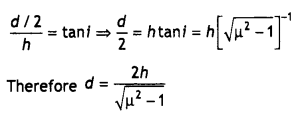
Question 16.
A ray of light is incident on a glass prism of refractive index μ and refracting angle A. If it just suffers total internal reflection at the other face, obtain an expression relating to the angle of incidence, angle of prism and critical angle.
Answer:
For a ray to just suffer total internal reflection at the second face of the prism r2 = ic
Now A = r1 + ic, therefore r1 = A – ic
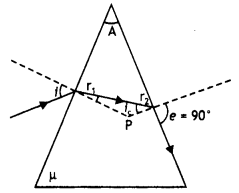
Now by Snells Law, we have
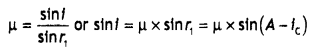
or
μ = \(\frac{\sin i}{\sin \left(A-1_{c}\right)}=\frac{1}{\sin i_{c}}\)
Question 17.
(a) Define, the refractive index of a medium.
(b) In the following ray diagram, calculate the speed of light In the liquid of unknown refractive index. (CBSE AI 2017C)
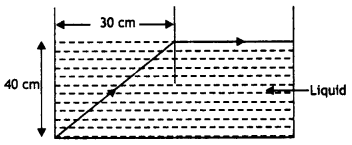
Answer:
(a) It is defined as the ratio of the speed of light in a vacuum to the speed of light in the given medium.
(b) The speed of Light can be found by using the formula
\(\frac{v}{c}=\frac{\sin 1}{\sin r}\)
or
v = \(\frac{\sin i}{\sin r}\) × c
From the diagram, we find that
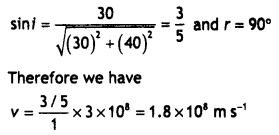
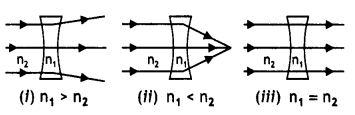
Question 18.
A concave lens made of material of refractive index n1 is kept In a medium of refractive index n2. A parallel beam of light is incident on the lens. Complete the path of the rays of light emerging from the concave lens If (i) n1 > n2 (ii) n1 < n2 and (iii) n1 n2
Answer:
The path of rays in the three cases is as shown.
Question 19.
A convex ten made of a material of refractive index n1 is kept in a medium of refractive index n2. A parallel beam of light is incident on the lens. Complete the path of rays of light emerging from the convex lens if (i) n1 > n2, (ii) n1 = n2, and (iii) n1 < n2.
Answer:
The path of the rays in the three cases is as shown.
Question 20.
Write the Lens Maker’s formula and use it to obtain the range of values of μ (the refractive index of the material of the lens) for which the focal length of an equi-convex lens, kept in air, would have a greater magnitude than that of the radius of curvature of its two surface. (CBSE Delhi 2016C)
Answer:
Lens maker’s formula is given by
\(\frac{1}{f}\) = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
For equiconvex Lens we have R1 = + R and
R2 = – R
Therefore we have
\(\frac{1}{f}\) = (n – 1)\(\frac{2}{R}\)
For f to be greater than R
2(n – 1) < 1
2n – 2 < 1
2n < 3
n < 1.5
Hence range is 1.0< n < 1.5
Question 21.
A ray of light passing from the air through an equilateral glass prism undergoes minimum deviation when the angle of Incidence is 3/4th of the angle of the prism. Calculate the sp..d of light In the prism. (CBSE AI 2017)
Answer:
Given A = 60°, i = 3/4 × 60 = 45°,
c = 3 × 108 m s-1,
Now δm = 2i – A
= 90 – 60 = 30°
Using the formula
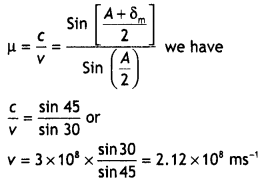
Question 22.
Calculate the value of the angle of Incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of the prism is \(\sqrt{2}\). (CBSE 2017C)
Answer:
The diagram is as shown.
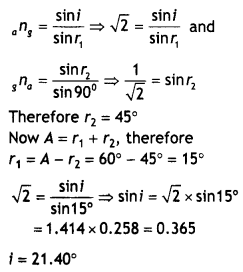
Question 23.
How is the working of a telescope different from that of a microscope?
The focal lengths of the objective and eyepiece of a microscope are 1.25 cm and 5 cm respectively. Find the position of the object relative to the objective in order to obtain an angular magnification of 30 in normal adjustment. (CBSE Delhi 2012)
Answer:
A microscope increases the size of the object whereas a telescope brings the object closer for better vision.
Given fo = 1.25 cm, fe = 5 cm, M = 30 cm, u = l
In normal adjustment final image is formed at infinity, therefore we have
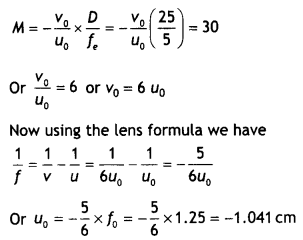
Question 24.
(a) Draw a labelled ray diagram showing the image formation of a distant object by a refracting telescope. Deduce the expression for its magnifying power when the final image is formed at infinity.
(b) The sum of focal lengths of the two lenses of a refracting telescope is 105 cm. The focal length of one lens is 20 times that of the other. Determine the total magnification of the telescope when the final image is formed at infinity. (CBSE AI 2014C)
Answer:
(a) For the diagram

From right triangles ABC and ABC’ as shown in figure, we have
tan α = \(\frac{\mathrm{AB}}{\mathrm{CB}}=\frac{-h}{f_{0}}\) and
tan β = \(\frac{\mathrm{AB}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{-h}{f_{\mathrm{e}}}\)
From the above we have we have
M = \(\frac{\beta}{\alpha}=\frac{-h}{f_{e}} \times \frac{f_{0}}{-h}=\frac{f_{0}}{f_{e}}\)
(b) L = 105 cm, fo = 20fe,
Now L = fo + fe = 21fe
Or
fe = 105/21 = 5 cm
Hence fo = 20 × fe 20 × 5 = 100 cm
Hence M = fo/fe = 100/ 5 = 20
Question 25.
(a) Explain with reason, how the power of a diverging lens changes when
(i) it is kept in a medium of refractive index greater than that of the lens.
(ii) Incident red light is replaced by violet light.
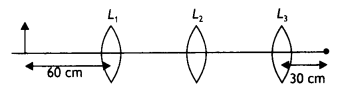
(b) Three lenses L1, L2, and L3 each of focal length 30 cm are placed coaxially as shown in the figure. An object is held at 60 cm from the optic centre of L1. The final image is formed at the focus of L3. Calculate the separation between (i) L1 and L2 and (ii) L2 and L3 (CBSE AI 2017C)
Answer:
(a) (i) The power of is given by the expression P = (n – 1)\(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) medium changes the power of the lens decreases as its focal length increases.
(ii) We know that f ∝ X, therefore a decrease in the wavelength from red to violet decreases the focal length and increases the power of the lens.
(b) Given f1 = f2 = f3 = 30 cm
For lens L1, u1 = 60 cm = 2f1, therefore the image will be formed at If on the other side of the lens L1.
Since the final image for lens L3 is formed at the focus, therefore the rays of light falling on lens L3 should come from infinity. This is possible if the image of L1 lies at the focus of L2.
Thus distance L1L2 = 60 + 30 = 90 cm
Also, distance L2L3 can have any value as the rays between L2 and L3 will be parallel.
Question 26.
Calculate the radius of curvature of an equi-concave lens of refractive Index 1.5, when It Is kept In a medium of refractive index 1.4, to have a power of -5 D?
OR
An equilateral glass prism has a refractive Index of 1.6 In the air. Calculate the angle of minimum deviation of the prism, when kept In a medium of refractive Index \(\frac{4 \sqrt{2}}{5}\). (CBSE Delhi 2019)
Answer:
Given nL = 1.5, nM = 1.4, P = -5 D
Focal length f \(\frac{1}{P}=\frac{1}{-5}=\frac{-100}{5}\) = 20 cm
Using the lens makers formula and putting
R1 = – R and
R2 = +R
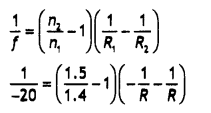
Solving for R, we get
R = 20/7 = 2.86cm
or
Given A = 60, n = 1.6, δm =?,nM = \(\frac{4 \sqrt{2}}{5}\)
Using the prism formula
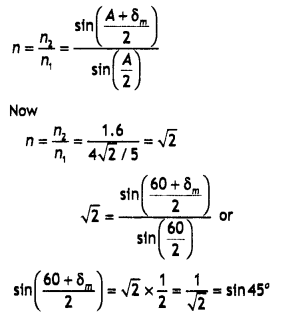
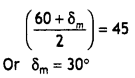
Question 27.
A ray of light passes through an equilateral glass prism, such that the angle of Incidence Is equal to the angle of emergence. If the angle of emergence is v times the angle of the prism, calculate the refractive index of the glass prism.
Answer:
Given the angle of prism A = 60°,
the angle of incidence i = angle of emergence ‘e’ and under this condition angle of deviation is minimum.
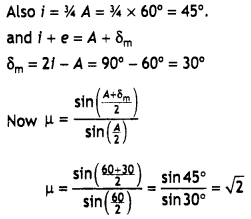
Question 28.
The magnifying power of an astronomical telescope In the normal adjustment position is 100. The distance between the objective and the eyepiece is 101 cm. Calculate the focal length of the objective and the eyepiece.
Answer:
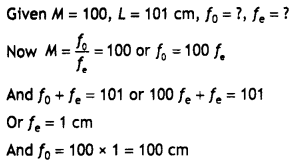
Question 29.
A double convex lens made of glass of refractive Index 1.5 has both radii of curvature of magnItude 20 cm. An object 2 cm high is placed at 10 cm from the lens. Find the position, nature and size of the image.
Answer:
Given n = 1.5 and for a double convex Lens R1 = + 20 cm and R2 = – 20 cm
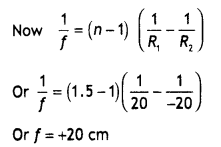
Now size of the object O = + 2 cm and u = – 1o cm
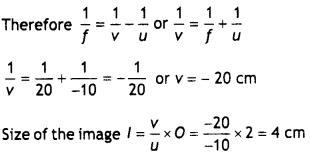
The image ¡s virtual and erect.
Question 30.
Three rays of light-red (R), green (G) and blue (B) are Incident on the face AB of a right-angled prism ABC. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively. Trace the path of the rays through the prism. How will the situation change if these rays were incident normally on one of the faces of an equilateral prism?
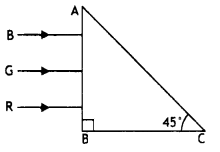
Answer:
The course of rays through the prism is as shown below.
Critical angle for a light ray is given by
sin ic = \(\frac{1}{n}\)
or
ic = sin-1\(\left(\frac{1}{n}\right)\)
Now critical angle for red ray (R)
iR = sin-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.39}\right)\) = 46°
Critical angle for green ray (G)
iG = sin-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.44}\right)\) = 44°
and Cnticat angLe for bLue ray (B)
iB = sin-1\(\left(\frac{1}{n}\right)\) = sin-1\(\left(\frac{1}{1.47}\right)\) = 42°52′
Thus the angle of incidence for blue and green rays inside the prism will be greater than the critical angle for these two colours. Therefore blue and green rays undergo total internal reflection. The angle of incidence for red colour is smaller than its critical angle; therefore it does not undergo total internal reflection. This is depicted in the figure below.
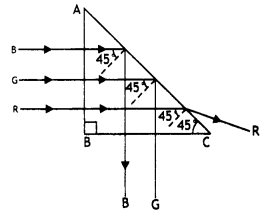
For an equilateral prism, the light rays pass through the prism suffering deviation. The angle of deviation δ = (n – 1) A. Hence, the deviation for red coloured ray will be the least and that for blue ray maximum. Paths of rays are shown in the figure below.
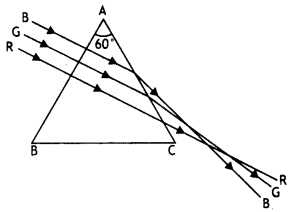
Question 31.
You are given three lenses of powers 0.5 D, 4 D, 10 D. State, with reason, which two lenses will you select for constructing a good astronomical telescope.
Calculate the resolving power of this telescope, assuming the diameter of the objective lens to be 6 cm and the wavelength of light used to be 540 nm.
Answer:
The focal lengths of the three lenses are
f1 = 1 /P1 = 1 / 0.5 = 2 m = 200 cm,
f2 = 1 /P2 = 1 / 4 = 0.25 m = 25 cm,
f3 = 1 /P3 = 1 /10 = 0. 1 m = 10 cm,
For an astronomical telescope, the objective should have a large focal length and the eyepiece should have a small focal length. Therefore for the objective, we will use the lenses of power 0.5 D and for the eyepiece the lens of power 10 D.
Given D = 6 cm = 0.06 m, λ = 540 nm = 540 × 10-9 m
Now resolving power
R.P. = \(\frac{D}{1.22 \lambda}=\frac{0.06}{1.22 \times 540 \times 10^{-9}}\) = 91074.6
Question 32.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different positions separated by 20 cm. Calculate the focal length of the lens.
OR
A convex lens of focal length 20 cm and a concave lens of focal length 15 cm are kept 30 cm apart with their principal axes coincident. When an object is placed 30 cm in front of the convex lens, calculate the position of the final image formed by the combination. Would this result change if the object were placed 30 cm In front of the concave tens? Give reason. (CBSE AI 2019)
Answer:
The image of an object can be obtained at two different positions of a convex lens for a fixed value of the distance between the object and the screen if values of u and v are interchanged in these two positions. This situation is as shown below.
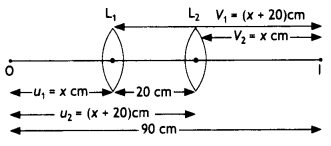
Here x + 20 + x = 90 cm or x = 35cm
Therefore, u = -35 cm, v = + 55 cm, f = ?
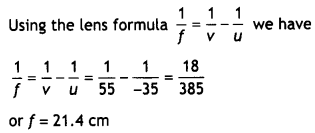
or
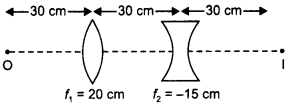
For image formed by a convex Lens
f1 = + 20 cm, u = – 30 cm
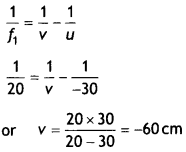
Therefore, u for concave Lens = 60 – 30 = + 30 cm and f2 = – 15 cm
Now for concave lens
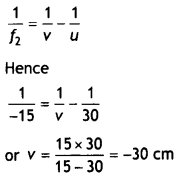
No, the result will not change as per the principle of reversibility.
Question 33.
For an equilateral glass prism, the minimum angle of deviation, for a parallel beam of monochromatic Incident light, is measured to be 30°. What is the refractive index of the glass used for making this prism?
If this prism were to be placed in a medium of refractive Index 1.414, how would a ray of light incident on one of its refracting faces pass through it? Draw the ray diagram for the same.
Answer:
Given A = 60°, δm = 30°, μ = ?
Using the relation
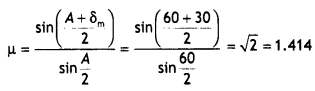
When this prism is placed in a medium of refractive index 1.414, it will behave like a plane glass piece as both the prism and the medium have the same refractive index.
The ray diagram is as shown.
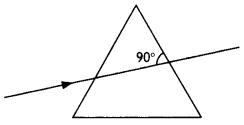
Question 34.
Find the position of the image formed by the lens shown in the figure.
Another lens is placed in contact with this lens to shift the image further away from the lens. What is the nature of the second lens?
Answer:
f = + 10 cm, u = – 30 cm, v =?
Using the lens equation we have
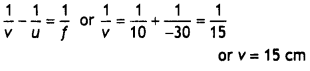
The second lens Is concave.
Question 35.
A beam of light of wavelength 400 nm is incident normally on a right-angled prism as shown. It is observed that the light just grazes along with the surface AC after falling on it. Given that the refractive index of the material of the prism varies with the wavelength as per the relation
μ = 1.2 + \(\frac{b}{\lambda^{2}}\) calculate the value of b and the refractive index of the prism material for a wavelength λ = 500 nm. [(Given θ = Sin-1 (0.625)]
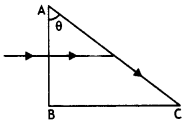
Answer:
The figure can be redrawn as shown below.
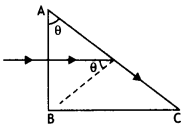
By symmetry angle, θ will be the critical angle.
Therefore
μ = \(\frac{1}{\sin \theta}=\frac{1}{0.625}\) = 1.6
Now the value of the constant b is obtained as follows:
μA = 1.2 + \(\frac{b}{\lambda^{2}}\)
or
1.6 = 1.2 + \(\frac{b}{(400)^{2}}\)
Solving for b we have b = 64000 nm2
Now for a wavelength λ = 500 nm the refractive index of the material of the prism is
μ = 1.2 + \(\frac{(64000)^{2}}{(500)^{2}}\) = 1.456
Question 36.
A convex lens, of focal length 20 cm, has a point object placed on its principal axis at a distance of 40 cm from It. A plane mirror Is placed 30 cm behind the convex lens. Locate the position of the image formed by this combination.
Answer:
We first consider the effect of the lens. For the Lens, we have
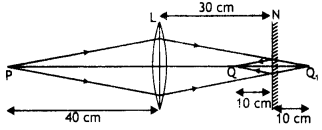
u = – 40 cm and f = + 20 cm
Using the lens formula, we get
\(\frac{1}{v}-\frac{1}{(-40)}=\frac{1}{20}\)
or
v = + 40 cm
Had there been the lens only the image would have been formed at Q1. The plane mirror M is at a distance of 30 cm from the lens L. We can, therefore, think of a Q1 as a virtual object, located at a distance of 10 cm, behind the plane mirror M. The plane mirror, therefore, forms a real image (of this virtual object Q1) at Q1, 10 cm in front of it. This is shown in the figure.
Question 37.
(i) Calculate the distance of an object of height h from a concave mirror of radius of curvature 20 cm, so as to obtain a real image of magnification 2. Find the location of the image also.
(ii) Using the mirror formula, explain why does a convex mirror always produce a virtual image. (CBSE Delhi 2016) Answer:
Given R = – 20 cm or f = – 10 cm, m = + 2 (real image), u = ?, v = ?
Using the relation m = \(\frac{f}{f-u}\) we have
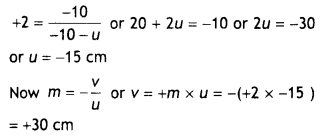
(b) For a convex mirror \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\) but f is positive and u is negative i.e., f > 0 but u < 0.
Therefore, it is self-evident from the above relation that irrespective of the value of u, the value of v is always +ve. It means that the image formed by a convex mirror is always virtual Independent of the location of the object.
Question 38.
A convex lens of focal length 20 cm and a concave mirror of focal length 10 cm are placed co-axially 50 cm apart from each other. An incident beam parallel to its principal axis is incident on the convex lens. Locate the position of the (final) image formed due to this combination.
Answer:
The incident beam, on lens L, is parallel to its principal axis. Hence the lens forms an image Q1 at its focal point, i.e. at a distance OQ1 (= 20 cm) from the lens. This image, Q1, now acts as a real object for the concave mirror. For the mirror, we then have: u = – 30 cm, and f = – 10 cm,
Hence using the mirror formula, we get
\(\frac{1}{v}+\frac{1}{(-30)}=\frac{1}{(-10)}\)
or
v = – 15 cm
The lens-mirror combination, therefore, forms a real image Q at a distance of 15 cm from M. The ray diagram is as shown in
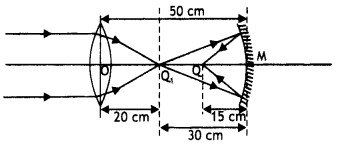
Question 39.
A convex lens of focal length 25 cm and a concave mirror of radius of curvature 20 cm are placed coaxially 40 cm apart from each other. An incident beam parallel to the principal axis is incident on the convex lens. Find the position and nature of the image formed by the combination. (CBSE Al 2016)
Answer:
The image of the object is formed at the focus of the convex lens, i.e. 25 cm. This image acts as an object for the concave mirror and ties at a distance (40 – 25) = 15 cm from the mirror.
Hence for the mirror
u = – 15 cm, v =? f = R/2 = 20/2 = 10 cm
Using mirror formula we have
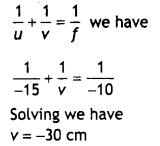
The image is formed in front of the mirror.
Question 40.
(i) A screen is placed at a distance of 100 cm from an object. The image of the object is formed on the screen by a convex lens for two different locations of the lens separated by 20 cm. Calculate the focal length of the lens used.
(ii) A converging lens is kept coaxially in contact with a diverging lens both the lenses being of equal focal length. What is the focal length of the combination? (CBSE AI 2016)
Answer:
(i) Given u + v= 100 or v= 100 – u
Using lens formula From lens first \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) we have

Or
f = 24 cm
(ii) f = infinity. \(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{-f_{2}}\) = 0
Question 41.
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. By rotating the prism, the angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light. The refracting angle of the prism is 60°. (NCERT)
Answer:
Given δm = 40°, aμg = ?, aμw = 1.33, A = 60°
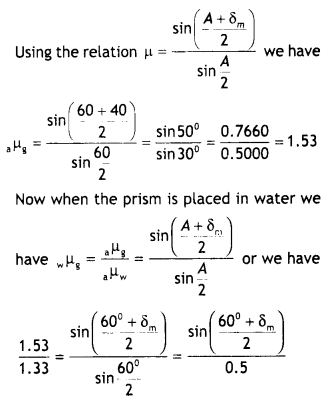
Solving for δm we have δm = 100°
Question 42.
A beam of light converges to a point P. A lens is placed in the path of the convergent beams 12 cm from P. At what point does the beam converge if the lens is
(i) a convex lens of focal length 20 cm,
Answer:
(i) Here u = 12 cm, f = + 20 cm and v = ?
Using the formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) we have
\(\frac{1}{v}=\frac{1}{12}+\frac{1}{20}=\frac{3+5}{60}=\frac{8}{60}\)
or
v = 7.5 cm
(ii) a concave lens of focal length 16 cm? (NCERT)
Answer:
Here u = 12 cm, f = – 16 cm and v =?
Using the formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)we have
\(\frac{1}{v}=\frac{1}{12}+\frac{1}{-16}=\frac{-3+4}{48}=\frac{1}{48}\)
or
v = 48 cm
Question 43.
A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (i) the least distance of distinct vision (25 cm), (ii) infinity? What is the magnifying power of the microscope in each case? (NCERT)
Answer:
Given f0 = 2.0 cm, fe = 6.25 cm, L = 15 cm, u0 = ?,
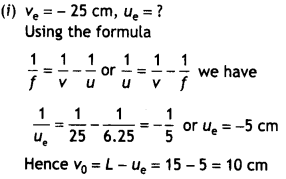
Now applying Lens formula for objective Lens we have \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u} \text { or } \frac{1}{u_{0}}=\frac{1}{v_{0}}-\frac{1}{f_{0}}\)


Question 44.
A small telescope has an objective lens of a focal length of 144 cm and an eyepiece of a focal length of 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece? (NCERT)
Answer:
Given fo = 144 cm, fe = 6.0 cm, M = ?,
L = fo + fe = ?
Using the formula M = \(\frac{f_{0}}{f_{e}}=\frac{144}{6}\) = 24 and
L = fo + fe = 144 + 6 = 150 cm
Question 45.
(a) A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope?
(b) If this telescope Is used to view the moon, what is the diameter of the Image of the moon formed by the objective lens? The diameter of the moon is 3.48 × 106 m, and the radius of lunar orbit Is 3.8 × 108 m. (NCERT)
Answer:
Given fo = 15 m, fe = 1.0 cm = 0.01 m, M = ?
Dm = 3.48 × 106 m, r = 3.8 × 108m,
(a) Using M = \(\frac{f_{0}}{f_{e}}=\frac{15}{0.01}\) = 1500
(b) AngLe subtended by moon at the objective of the teLescope
α = \(\frac{D_{m}}{r}=\frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}\)
Therefore angLe subtended by the image
β = M × α = 1500 × \(\frac{3.48 \times 10^{6}}{3.8 \times 10^{8}}\)
If I be the Linear size of the image then
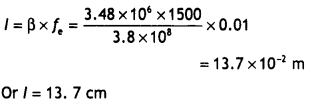
Question 46.
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524. (NCERT)
Answer:
Given A = 60°, i = ?, μ = 1.524
For a ray to just suffer total internal reflection at the second face of the prism r2 = ic
Now sin ic = \(\frac{1}{\mu}=\frac{1}{1.524}\) = 0.6562
or
ic = 41°
Now A = r1 + r2, therefore r1 = A – r2
r1 = 60 – 41 = 19°
Now by Snell’s law we have
μ = \(\frac{\sin i}{\sin r_{1}}\)
or
sin i = μ × sinr1 = 1.524 × sin 19°
or
i = 29.75° = 30°
Question 47.
A small telescope has an objective lens of a focal length of 140 cm and an eyepiece of a focal length of 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when
(a) the telescope is in normal adjustment (i.e. when the final image is at infinity.
Answer:
Given fo = 140 cm, fe = 5.0 cm, M = ?
For normal adjustment we have
M = \(\frac{f_{0}}{f_{e}}=\frac{140}{5}\) = 28
(b) the final image is formed at the least distance of distinct vision (25 cm) (NCERT)
Answer:
When the final image is formed at the least distance of distinct vision we have
M = \(\frac{f_{0}}{f_{e}}\left(1+\frac{f_{e}}{D}\right)=\frac{140}{5}\left(1+\frac{5}{25}\right)\) = 33.6
Question 48.
(a) The refractive index of glass is 1.5. What is the speed of light In a glass? (Speed of light in a vacuum is 3.0 × 108 ms-11 )
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
(a) Given μ = 1.5, c = 3.0 × 108 m s-1
v = \(\frac{c}{\mu}=\frac{3 \times 10^{8}}{1.5}\) = 2.0 × 108 ms-1
(b) No. The refractive index, and hence the speed of light in a medium, depends on wavelength. When no particular wavelength or colour of light is specified, we may take the given refractive index to refer to yellow colour or mean light. Now we know violet colour deviates more than red in a glass prism, i.e. μv > μR. Therefore, the violet component of white light travels slower than the red component.
Question 49.
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices μ1 > μ2 > μ3 are put in a beaker. The height of each liquid column is d3. A dot is made at the bottom of the beaker. For near-normal vision, find the apparent depth of the dot. (NCERT Exemplar)
Answer:
The situation is as shown.
Let the apparent depth be O1 for the object as seen from μ2, then
Apparent depth = real depth/μ
O1 = \(\frac{h / 3}{\mu_{1} / \mu_{2}}=\frac{\mu_{2} h}{3 \mu_{1}}\)
If seen from O3 the apparent depth O2 is
Apparent depth = real depth/μ
O2 = \(\frac{\left(h / 3+O_{1}\right)}{\mu_{2} / \mu_{3}}=\frac{\mu_{3}}{\mu_{2}}\left(\frac{h}{3}+\frac{\mu_{2}}{\mu_{1}} \frac{h}{3}\right)\)
Seen from outside the apparent height is
Apparent depth = real depth/μ
Question 50.
For a glass prism (μ = \(\sqrt{3}\)) the angle of minimum deviation Is equal to the angle of the prism. Find the angle of the prism. (NCERT Exemplar)
Answer:
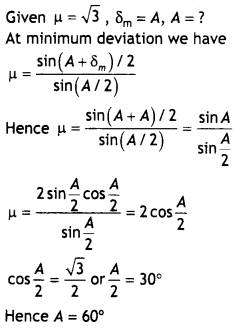
Question 51.
In many experimental set-ups, the source and screen are fixed at a distance say D and the lens Is movable. Show that there are two positions for the lens for which an image Is formed on the screen. Find the distance between these points and the ratio of the Image sizes for these two points. (NCERT Exemplar)
Answer:
The situation is shown.
If there was no cut then the object would have been at a height of 0.5 cm from the principal axis OO’. Consider the image for this case by lens formuLa we have
\(\frac{1}{v}=\frac{1}{u}+\frac{1}{f}=\frac{1}{-50}+\frac{1}{25}=\frac{1}{50}\)
Or
v = 50 cm
Hence magnification of the image is.
m = \(\frac{v}{u}=\frac{-50}{50}\) = -1
Thus the image would have been formed at 50 cm from the pole and 0.5 cm below the principal axis. Hence with respect to the X-axis passing through the edge of the cut lens, the co-ordinates of the image are (50 cm, -1 cm)