Constructions Class 10 Notes Maths Chapter 11

On this page, you will find Constructions Class 10 Notes Maths Chapter 11 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 11 Constructions will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 11 Notes Constructions

Constructions Class 10 Notes Understanding the Lesson

Division of a line segment internally in the given ratio.

Let AB be a line segment of certain length. We need a point P on AB dividing it internally in the ratio m : n
Steps of Construction: Let m = 4, n = 3.

• Draw a line segment AB of given length.
• Make an acute ∠BAX with AB
• Use a compass of any radius and mark 7(i.e. m + n) points A₁, A₂,…… , A₇
  such that AA₁ = A₁A₂ = A₂A₃ =………………= A₆A₇
  
  
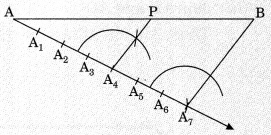
• Join BA₇
• Through the point A₄ [m = 4], draw a line parallel to BA₇ by making an angle equal to AA₇B at A₄ intersecting AB at P. Then AP : PB = 4 : 3.

Construction of a Triangle similar to a given Triangle as per given scale factor.
1. Scale Factor  \(\frac{m}{n}\)(where m < n)
Steps of construction: Let \(\frac{m}{n}=\frac{3}{4}\)

• Construct a triangle ABC by using given data.
• Make an acute angle ∠BAX below the base AB.
• Along AX, mark 4 points [the greater of 3 and 4 in \(\frac{3}{4}\)] as A₁, A₂,A₃, A₄ such that
  AA₁ = A₁A₂ = A₂A₃ = A₃A₄.
• Join A₄ B
  
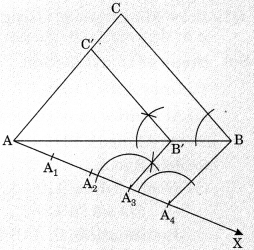
• From A₃, draw A_gB’ || A₄B, meeting AB at B’.
  From B’, draw B’C’ || BC, meeting AC at C’.

Thus, ΔAB’C’ is the required triangle each of whose sides is \(\frac{3}{4} \)of the corresponding side of ΔABC.

2. Scale Factor \(\frac{m}{n} \) (where m > n)
Steps of construction:
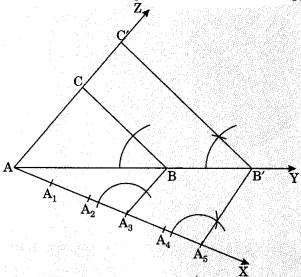
Let \(\frac{m}{n}=\frac{5}{3}\)

• Construct ΔABC using given data.
• Make an acute angle ∠BAX below the base AB. Extend AB to AY and AC to AZ.

• Along AX, mark 5 points [the greater of 5 and 3 in \(\frac{5}{3} \)
  such that AA₁ = A₁A₂ =………. = A₄A₅.
• Join A₃B.
• From A_g, draw A₅B’ || A₃B, meeting AY produced at B’.
• From B’, draw B’C’ || BC, meeting AZ produced at C’.
  Thus, ΔAB’C’ is the required triangle, each of whose sides is \(\frac{5}{3}\) of the corresponding side of ΔABC.

Construction of the pair of tangents from an external point to a circle.

Let O is the centre of the circle and a point A is external point to a circle.

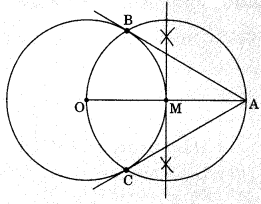
Steps of construction

• Join AO and bisect it. Let M be the mid-point of AO.
• Taking M as centre and MO as radius, draw a circle.
  Let it intersects the given circle at the points B and C.
• Join AB and AC.
  Thus, AB and AC are the required tangents.