ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test
Question 1.
Draw a straight line AB of length 8 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
Solution:
(i) Draw a line segment AB = 8 cm.
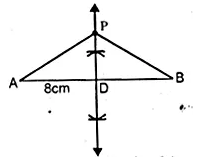
(ii) Draw the perpendicular bisector of AB intersecting AB at D.
∴ Every point P on it will be equidistant from A and B.
(iii) Take a point P on the perpendicular bisector.
(iv) Join PA and PB.
Proof: In ∆PAD and ∆PBD
PD = PD (common)
AD = BD (D is mid-point of AB)
∠PDA = ∠PDB (each 90°)
∴ ∆ PAD ≅ ∆ PBD (SAS axiom of congruency)
∴PA = PB (c.p.c.t.)
Similarly, we can prove any other point on the
perpendicular bisector of AB is equidistant from A and B.
Hence Proved.
Question 2.
A point P is allowed to travel in space. State the locus of P so that it always remains at a constant distance from a fixed point C.
Solution:
The point P is moving in the space and
it is at a constant distance from a fixed point C.
∴ Its locus is a sphere.
Question 3.
Draw a line segment AB of length 7 cm. Construct the locus of a point P such that area of triangle PAB is 14 cm².
Solution:
Base of ∆PAB = 7 cm
and its area = 14 cm²
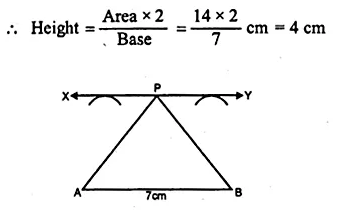
Now draw a line XY parallel to AB at a distance of 4 cm.
Now take any point P on XY
Join PA and PB
area of ∆PAB = 14 cm.
Hence locus of P is the line XY
which is parallel to AB at a distance of 4 cm.
Question 4.
Draw a line segment AB of length 12 cm. Mark M, the mid-point of AB. Draw and describe the locus of a point which is
(i) at a distance of 3 cm from AB.
(ii) at a distance of 5 cm from the point M. Mark the points P, Q, R, S which satisfy both the above conditions. What kind of quadrilateral is PQRS? Compute the area of the quadrilateral PQRS.
Solution:
Steps of Construction :
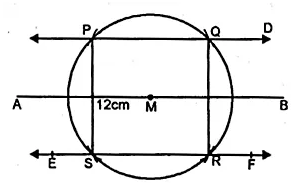
(i) Take a line AB = 12 cm
(ii) Take M, the midpoint of AB.
(iii) Draw straight lines CD and EF parallel to AB at a distance of 3 cm.
(iv) With centre M and radius 5 cm,
draw areas which intersect CD at P and Q and EF at R and S.
(v) Join QR and PS.
PQRS is a rectangle where the length PQ = 8 cm.
Area of rectangle PQRS = PQ x RS = 8 x 6 = 48 cm²
Question 5.
AB and CD are two intersecting lines. Find the position of a point which is at a distance of 2 cm from AB and 1.6 cm from CD.
Solution:
(i) AB and CD are the intersecting lines which intersect each other at O.
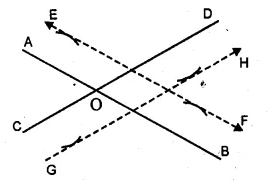
(ii) Draw a line EF parallel to AB and GH parallel to CD intersecting each other at P
P is the required point.
Question 6.
Two straight lines PQ and PK cross each other at P at an angle of 75°. S is a stone on the road PQ, 800 m from P towards Q. By drawing a figure to scale 1 cm = 100 m, locate the position of a flagstaff X, which is equidistant from P and S, and is also equidistant from the road.
Solution:
1 cm = 100 cm
800 m = 8 cm.
Steps of Construction :
(i) Draw the lines PQ and PK intersecting each other
at P making an angle of 75°.
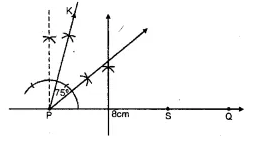
(ii) Take a point S on PQ such that PS = 8 cm.
(iii) Draw the perpendicular bisector of PS.
(iv) Draw the angle bisector of ∠KPS intersecting
the perpendicular bisector at X.
X is the required point which is equidistant from P and S
and also from PQ and PK.
Question 7.
Construct a rhombus PQRS whose diagonals PR, QS are 8 cm and 6 cm respectively. Find by construction a point X equidistant from PQ, PS and equidistant from R, S. Measure XR.
Solution:
Steps of Construction :
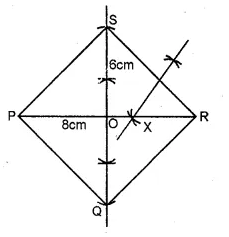
(i) Take PR = 8 cm and draw the perpendicular bisector
of PR intersecting it at O.
(ii) From O, out. off OS = OQ = 3 cm
(iii) Join PQ, QR, RS and SP.
PQRS is a rhombus. Whose diagonal are PR and QS.
(iv) PR is the bisector of ∠SPQ.
(v) Draw the perpendicular bisector of SR intersecting PR at X
∴ X is equidistant from PQ and PS and also from S and R.
On measuring length of XR = 3.2 cm (approx)
Question 8.
Without using set square or protractor, construct the parallelogram ABCD in which AB = 5.1 cm. the diagonal AC = 5.6 cm and the diagonal BD = 7 cm. Locate the point P on DC, which is equidistant from AB and BC.
Solution:
Steps of Construction :
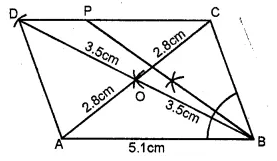
(i) Take AB = 5.1 cm
(ii) At A, with readius \(\\ \frac { 5.6 }{ 2 } \) = 2.8 cm
and at B with radius \(\\ \frac { 7.0 }{ 2 } \) = 3.5 cm,
draw two arcs intersecting each other at O.
(iii) Join AO and produce it to C such that
OC = AD = 2.8 cm and
join BO and produce it to D such that
BO = OD = 3.5 cm
(iv) Join BC, CD, DA
ABCD is a parallelogram.
(v) Draw the angle bisector of ∠ABC intersecting CD at P.
P is the required point which is equidistant from AB and BC.
Question 9.
By using ruler and compass only, construct a quadrilateral ABCD in which AB = 6.5 cm, AD = 4cm and ∠DAB = 75°. C is equidistant from the sides AB and AD, also C is equidistant from the points A and B.
Solution:
Steps of Construction :
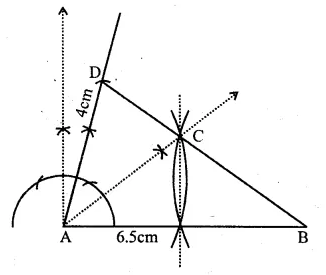
(i) Draw a line segment AB = 6.5 cm.
(ii) At A, draw a ray making an angle of 75° and cut off AD = 4 cm.
(iii) Draw the bisector of ∠DAB.
(iv) Draw perpendicular bisector of AB intersecting the angle bisector at C.
(v) Join CB and CD.
ABCD is the required quadrilateral.
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.