ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test
Question 1.
A student scored the following marks in 11 questions of a question paper : 3, 4, 7, 2, 5, 6, 1, 8, 2, 5, 7 Find the median marks.
Solution:
Arranging in the ascending order, 1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 8
Here, n = 11 i.e. odd,
The middle term = \(\\ \frac { n+1 }{ 2 } \) = \(\\ \frac { 11+1 }{ 2 } \) = \(\\ \frac { 12 }{ 2 } \) = 6th term
Median = 5
Question 2.
(a) Find the median of the following set of numbers : 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7 (1990)
(b)For the following set of numbers, find the median: 10, 75, 3, 81, 17, 27, 4, 48, 12, 47, 9, 15.
Solution:
(a) Arranging in ascending order :
0, 1, 2, 2, 3, 4, 5, 5, 5, 7, 8, 9
Here, n = 12 which is even

Question 3.
Calculate the mean and the median of the numbers : 2, 1, 0, 3, 1, 2, 3, 4, 3, 5
Solution:
Writing in ascending order 0, 1, 1, 2, 2, 3, 3, 3, 4, 5
Here, n = 10 which is even
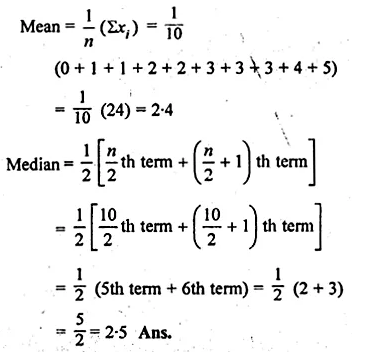
Question 4.
The median of the observations 11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24. Find the value of x and hence find the mean.
Solution:
Observation are :
11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47
n = 9
Median = \(\\ \frac { 9+1 }{ 2 } \) th term
i.e, 5th term = x + 4

Question 5.
The mean of the numbers 1, 7, 5, 3, 4, 4, is m. The numbers 3, 2, 4, 2, 3, 3, p have mean m – 1 and median q. Find
(i) p
(ii) q
(iii) the mean of p and q.
Solution:
(i) Mean of 1, 7, 5, 3, 4, 4 is m.
Here n = 6
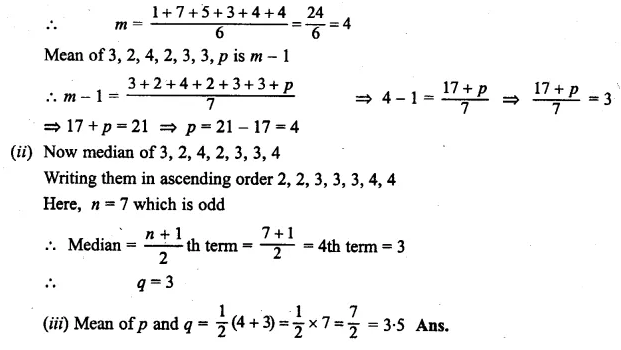
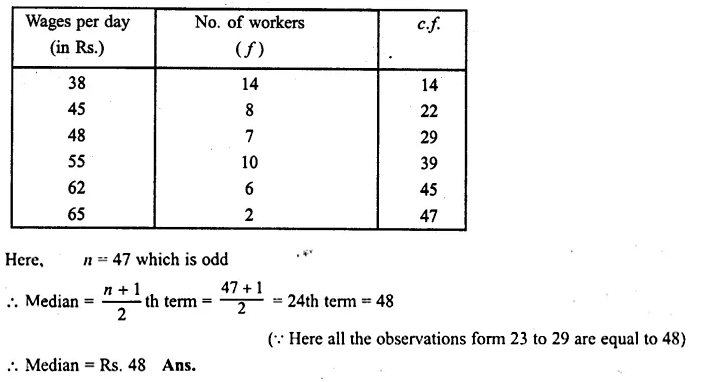
Question 6.
Find the median for the following distribution:

Solution:
Writing the distribution in cumulative frequency table:
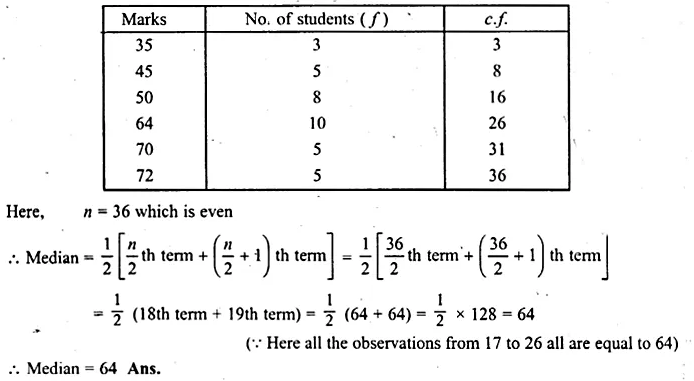
Question 7.
Find the median for the following distribution.

Solution:
Writing the distribution in cumulative frequency table :
Question 8.
Marks obtained by 70 students are given below :

Calculate the median marks.
Solution:
Arranging the variates in ascending order and in c.f. table.

Question 9.
Calculate the mean and the median for the following distribution :

Solution:
Writing the distribution in c.f. table :

Question 10.
The daily wages (in rupees) of 19 workers are
41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, 35.
Find
(i) the median
(ii) lower quartile
(iii) upper quartile range,
(iv) interquartile range.
Solution:
Arranging the observations in ascending order
21, 23, 25, 26, 27, 28, 29, 29, 30, 31, 31, 35, 35, 38, 41, 42, 45, 47, 53
Here n = 19 which is odd.
(i) Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 19+1 }{ 2 } \) = \(\\ \frac { 20 }{ 2 } \) = 10th term = 31
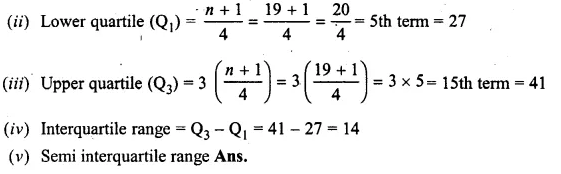
Question 11.
From the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range

Solution:
Writing frequency distribution in c.f. table :

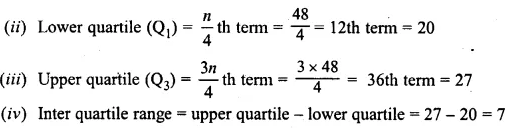
Question 12.
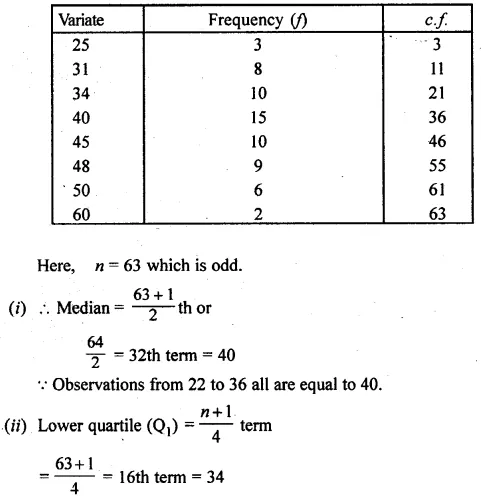
For the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile

Solution:
Writing the distribution in cumulative frequency (c.f.) table :
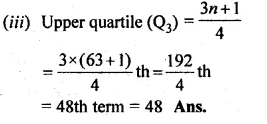
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2, drop a comment below and we will get back to you at the earliest.