NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.4.

Board CBSE
Textbook NCERT
Class Class 8
Subject Maths
Chapter Chapter 3
Chapter Name Understanding Quadrilaterals
Exercise Ex 3.4
Number of Questions Solved 6
Category NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.4

Question 1.
State whether True or False :
(a) All rectangles are squares
(b) All rhombuses are parallelograms
(c) All squares are rhombuses and also rectangles
(d) All squares are not parallelograms
(e) All kites are rhombuses
(f) All rhombuses are kites
(g) All parallelograms are trapeziums
(h) All squares are trapeziums.
Solution.
(b), (c), (f), (g), (h) are true;
others are false.

Question 2.
Identify all the quadrilaterals that have.
(a) four sides of equal length
(b) four right angles
Solution.
(a) Rhombus; square
(b) Square; rectangle

Question 3.
Explain how a square is
(i) a quadrilateral
(ii)a parallelogram
(iii) a rhombus
(iv) a rectangle.
Solution.
(i) a quadrilateral
A square is 4 sided, so it is a quadrilateral.

(ii) a parallelogram
A square has its opposite sides parallel; so it is a parallelogram.

(iii) a rhombus
A square is a parallelogram with all the 4 sides equal, so it is a rhombus.

(iv) a rectangle
A square is a parallelogram with each angle a right angle; so it is a rectangle.

Question 4.
Name the quadrilaterals whose diagonals :
(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal.
Solution.
(i) bisect each other
The names of the quadrilaterals whose diagonals bisect each other are parallelogram; rhombus; square; rectangle.

(ii) are perpendicular bisectors of each other
The names of the quadrilaterals whose diagonals are perpendicular bisectors of each other are rhombus; square.

(iii) are equal
The names of the quadrilaterals whose diagonals are equal are square; rectangle.

Question 5.
Explain why a rectangle is a convex quadrilateral.
Solution.
A rectangle is a convex quadrilateral because both of its diagonals lie wholly in its interior.

Question 6.
ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
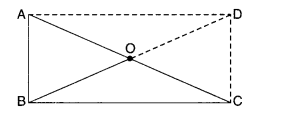
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.4 1
Solution.
Construction: Produce BO to D such that BO = OD. Join AD and CD.
Proof. AO = OC ∵ O is the mid-point of AC
BO = OD By construction
∴ Diagonals of quadrilateral ABCD bisect each other.
∴ Quadrilateral ABCD is a parallelogram.
Now, ∠ABC = 90° given
∴ ABCD is a rectangle.
Since the diagonals of a rectangle bisect each other, therefore,
O is the mid-point of AC and BD both. But AC = BD
∵ Diagonals of a rectangle are equal
∴ OA = OC =\(\frac { 1 }{ 2 } \)AC =\(\frac { 1 }{ 2 } \)BD = OB
⇒ OA = OB = OC.

We hope the NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.4 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.4, drop a comment below and we will get back to you at the earliest.