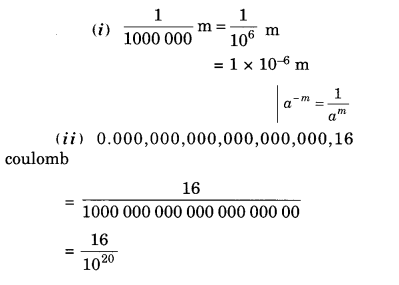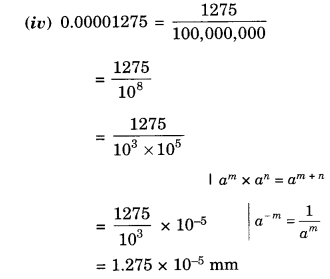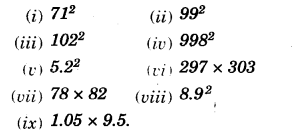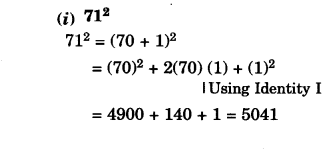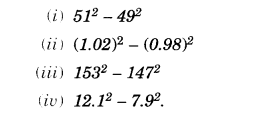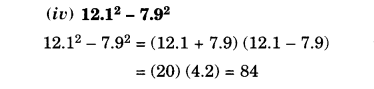Tag: NCERT Solutions for Class 8 Maths

NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.2.

• Playing with Numbers Class 8 Ex 16.1

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 16
Chapter Name	Playing with Numbers
Exercise	Ex 16.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.2

Question 1.
If 21y5 is a multiple of 9, where y is a digit, what is the value of y?
Solution.
Since 21y5 is a multiple of 9, its sum of digits 2 + 1+ y + 5 = 8+ y isa multiple of 9; so 8 + y is one of these numbers: 0, 9, 18, 27, 36, 45,… .
But since y is a digit, it can only be possible that 8 + y = 9. Therefore, y = 1.

Question 2.
If 31z5 is a multiple of 9, where z is a digit, what is the value of z?
You will find that there are two answers to the last problem. Why is this so?
Solution.
Since 31z5 is a multiple of 9, its sum of digits 3 + 1 + z + 5 = 9 + z isa multiple of 9; so 9 + z is one of these numbers: 0, 9, 18, 27, 36, 45, … .
But since z is a digit, it can only be possible that 9 + z = 9 or 18. Therefore, z = 0 or 9.

Question 3.
If 24x is a multiple of 3, where x is a digit, what is the value of x?
(Since 24x is a multiple of 3, its sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers: 0, 3, 6, 9, 12, 15, 18, … .
But since xis a digit, it can only be that 6 + x = 6 or 9 or 12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of four different values.)
Solution.
The solution is given with question.

Question 4.
If 31z5 is a multiple of 3, where z is a digit, what might be the values of z?
Solution.
Since 31z5 is a multiple of 3, its sum of digits 3 + 1 + z + 5 = 9 + z is a multiple of 3; so 9 + z is one of these numbers: 0, 3, 6, 9, 12, 15, 18, … .
But since z is a digit, it can only be possible that 9 + z = 9 or 12 or 15 or 18. Therefore, z = 0 or 3 or 6 or 9.

We hope the NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.3.

• Introduction to Graphs Class 8 Ex 15.1
• Introduction to Graphs Class 8 Ex 15.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 15
Chapter Name	Introduction to Graphs
Exercise	Ex 15.3
Number of Questions Solved	2
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.3

Question 1.
Draw the graphs for the following tables of values, with suitable scales on the axes.
(a) Cost of apples

(b) Distance travelled by a car

(i) How much distance the car cover during the period 7.30 a.m. to 8 a.m.?
(ii) What was the time when the car had covered a distance of 100 km since it starts?

(c) Interest on deposits for a year.

(i) Does the graph pass through the origin?
(ii) Use the graph to find the interest on? 2500 for a year.
(iii) To get an interest of ? 280 per year, how much money should be deposited?
Solution.
(a)

Scale:
On horizontal axis:         2 units = 1 apple
On vertical axis:              1 unit = ₹ 5
• Mark number of apples on the horizontal axis.
• Mark cost (in ?) on the vertical axis.
• Plot the points: (1, 5), (2, 10), (3, 15), (4, 20) and (5, 25)
• Join the points.
We get a linear graph.

(b)

Scale:
On horizontal axis:      2 units = 1 hour
On vertical axis:           2 units = 40 km
• Mark time (in hours) on the horizontal axis.
• Mark distances (in km) on the vertical axis.
• Plot the points (6 a.m., 40), (7 a.m., 80) (8 a.m., 120) and (9 a.m., 160).
• Join the points.
We get a linear graph.
(i) Distance covered during 7.30 a.m. to 8 a.m.
= 120 km – 100 km = 20 km
(ii) The time when the car had covered a distance of 100 km since its start was 7.30 a.m.

(c)
Scale:
On horizontal axis:       2 units = ₹ 1000
On vertical axis:            2 units = ₹ 80
• Mark deposit (in ₹ on the horizontal axis.
• Mark simple interest (in ₹) on the vertical axis.
• Plot the points (1000, 80), (2000, 160), (3000, 240) (4000, 320) and (5000, 400).
• Join the points.
We get a linear graph.
(i) Yes! The graph passes through the origin.
(ii) Interest on ₹ 2500 for a year = ₹ 200
(iii) To get an interest of ₹ 280 per year, ₹ 3500 should be deposited.

Question 2.
Draw a graph for the following:
(i)

Is it a linear graph?
(ii)

Is it a linear graph?
Solution.
(i)

Scale:
On horizontal axis:     1 unit = 1 cm
On vertical axis:          1 unit = 4 cm
• Mark side of the square (in cm) on the horizontal axis.
• Mark perimeter (in cm) on the vertical axis.
• Plot the points (2, 8), (3, 12), (3.5. 14) (5, 20) and (6, 24).
• Join the points.
Yes ; it is a linear graph.

(ii)

• Scale:
On horizontal axis: 2 units = 2 cm
On vertical axis: 1 unit = 2 cm
• Mark side of the square (in cm) on the horizontal axis.
• Mark area (in cm ) on the vertical axis.
• Plot the points (2, 4) (3, 9), (4, 16), (5, 25) and (6, 36).
• Join the points.
The graph we get is not linear.

We hope the NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.2.

• Introduction to Graphs Class 8 Ex 15.1
• Introduction to Graphs Class 8 Ex 15.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 15
Chapter Name	Introduction to Graphs
Exercise	Ex 15.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.2

Question 1.
Plot the following points on a graph sheet. Verify if they lie on a line.
(a) A(4, 0), B(4, 2), C(4, 6), D(4, 2.5)
(b) P(l, 1), Q(2, 2), R(3, 3), S(4, 4)
(c) K(2, 3), L(5, 3), M(5, 5), N(2, 5)
Solution.

(a) The points lie on a line.
(b) The points lie on a line.
(c) The points do not lie on a line.

Question 2.
Draw the line passing through (2, 3) and (3, 2). Find the coordinates of the points at which this line meets the x-axis and y-axis.
Solution.
The coordinates of the points at which this line meets the x-axis and y-axis are (5, 0) and (0, 5) respectively. See the graph given above.

Question 3.
Write the coordinates of the vertices of each of these adjoining figures.

Solution.
O → (0, 0)
A → (2,0)
B → (2, 3)
C → (0,3)

P → (4, 3)
Q → (6, 1)
R → (6, 5)
S → (4, 7)

K → (10, 5)
L → (7, 7)
M → (10, 8)

Question 4.
State whether True or False. Correct that is false.
(i) A point whose x-coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
(ii) A point whose y-coordinate is zero ‘ and x-coordinate is 5 will lie on y-axis.
(iii) The coordinates of the origin are (0, 0).
Solution.
(i) True
(ii) False; A point whose y-coordinate is zero and x-coordinate is 5 will lie on x-axis.
(iii) True

 

We hope the NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.4.

• Factorisation Class 8 Ex 14.1
• Factorisation Class 8 Ex 14.2
• Factorisation Class 8 Ex 14.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 14
Chapter Name	Factorisation
Exercise	Ex 14.4
Number of Questions Solved	21
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.4

Find and correct the errors in the following mathematical statements.
Question 1.
4(x – 5) = 4x – 5
Solution.
4(x – 5) = 4x – 20

Question 2.
x(3x + 2) = \({ 3x }^{ 2 }+2\)
Solution.
x(3x + 2) = \({ 3x }^{ 2 }+2x\)

Question 3.
2x + 3y = 5xy
Solution.
2x + 3y = 2x + 3y

Question 4.
x + 2x + 3x = 5x
Solution.
x + 2x + 3x = 6x

Question 5.
5y + 2y + y – 7y = 0
Solution.
5y + 2y + y – 7y – y

Question 6.
3x + 2x = \({ 5x }^{ 2 }\)
Solution..
3x + 2x = 5x

Question 7.
\({ \left( 2x \right) }^{ 2 } + 4(2x) + 7 = { 2x }^{ 2 } + 8x + 7 \)
Solution.
\({ \left( 2x \right) }^{ 2 } + 4(2x) + 7 = { 4x }^{ 2 } + 8x + 7 \)

Question 8.
\({ \left( 2x \right) }^{ 2 } + 5x = 4x + 5x = 9x \)
Solution.
\({ \left( 2x \right) }^{ 2 } + 5x = { 4x }^{ 2 } + 5x \)

Question 9.
\({ \left( 3x+2 \right) }^{ 2 } = { 3x }^{ 2 } + 6x + 4. \)
Solution.
\({ \left( 3x+2 \right) }^{ 2 } = { 9x }^{ 2 }+ 12x + 4. \)

Question 10.

Solution.

Question 11.
\({ \left( y-3 \right) }^{ 2 } = { y }^{ 2 } – 9 \)
Solution.
\({ \left( y-3 \right) }^{ 2 } = { y }^{ 2 } – 2(y)(3) + { 3 }^{ 2 }\)
= \({ y }^{ 2 } – 6y + 9 \)
and not equal to \({ y }^{ 2 } – 9 \)

Question 12.
\({ \left( z+5 \right) }^{ 2 } = { z }^{ 2 } + 25 \)
Solution.
\({ \left( z+5 \right) }^{ 2 } = { z }^{ 2 } + 2(z) (5) + { 5}^{ 2 }\)
= \({ z }^{ 2 } + 10z + 25 \)
and not equal to \({ z }^{ 2 } + 25 \)

Question 13.
\(\left( 2a+36 \right) \left( a-b \right) = { 2a }^{ 2 }-{ 3b }^{ 2 }\)
Solution.

Question 14.
\(\left( a+4 \right) \left( a+2 \right) = { a}^{ 2 } + 8 \)
Solution.

Question 15.
\(\left( a-4 \right) \left( a-2 \right) = { a}^{ 2 }-8 \)
Solution.

Question 16.
\(\frac { { 3x }^{ 2 } }{ { 3x }^{ 2 } } =0\)
Solution.
\(\frac { { 3x }^{ 2 } }{ { 3x }^{ 2 } } =1\) and not equal to 0

Question 17.
\(\frac { { 3x }^{ 2 }+1 }{ { 3x }^{ 2 } } =1+1=2\)
Solution.
\(\frac { { 3x }^{ 2 }+1 }{ { 3x }^{ 2 } } =\frac { { 3x }^{ 2 } }{ { 3x }^{ 2 } } +\frac { 1 }{ { 3x }^{ 2 } } \)
=\(1+\frac { 1 }{ { 3x }^{ 2 } }\) and not equal to 1 + 1 = 2

Question 18.
\(\frac { 3x }{ 3x+2 } =\frac { 1 }{ 2 } \)
Solution.
\(\frac { 3x }{ 3x+2 } =\frac { 3x }{ 3x+2 } \) and not equal to \(\frac { 1 }{ 2 }\)

Question 19.
\(\frac { 3 }{ 4x+3 } =\frac { 1 }{ 4x } \)
Solution.
\(\frac { 3 }{ 4x+3 } =\frac { 3 }{ 4x+3 } \) and not equal to \(\frac { 1 }{ 4x }\)

Question 20.
\(\frac { 4x+5 }{ 4x } =5\)
Solution.
\(\frac { 4x+5 }{ 4x } =\frac { 4x }{ 4x } +\frac { 5 }{ 4x } =1+\frac { 5 }{ 4x } \) and not equal to 5

Question 21.
\(\frac { 7x+5 }{ 5 } =7x\)
Solution.
\(\frac { 7x+5 }{ 5 } =\frac { 7x }{ 5 } +\frac { 5 }{ 5 } =\frac { 7x }{ 5 } +1\) and not equal to 7x

We hope the NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.4 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1.

• Factorisation Class 8 Ex 14.1
• Factorisation Class 8 Ex 14.2
• Factorisation Class 8 Ex 14.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 14
Chapter Name	Factorisation
Exercise	Ex 14.3
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.3

Question 1.
Carry out the following divisions:

Solution.

Question 2.
Divide the given polynomial by the given monomial:

Solution.

Question 3.
Work out the following divisions:

Solution.

Question 4.
Divide as directed.

Solution.

Question 5.
Factorise the expressions and divide them as directed.

Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.2.

• Direct and Indirect Proportions Class 8 Ex 13.1

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 13
Chapter Name	Direct and Indirect Proportions
Exercise	Ex 13.2
Number of Questions Solved	11
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.2

Question 1.
Which of the following are in inverse proportion?
(i) The number of workers on a job and the time to complete the job.
(ii) The time is taken for a journey and the distance traveled in a uniform speed.
(iii) Area of cultivated land and the crop harvested.
(iv) The time is taken for a fixed journey and the speed of the vehicle.
(v) The population of a country and the area of land per person.
Solution.
(i) The number of workers on jobs and the time to complete the job are in inverse proportion.
(ii) The time is taken for a journey and the distance traveled in a uniform speed are not in inverse proportion.
(iii) Area of cultivated land and the crop harvested are not in inverse proportion.
(iv) The time taken for a fixed journey and the speed of the vehicle are in inverse proportion.
(v) The population of a country and the area of land per person are in inverse proportion.

Question 2.
In a Television game show, the prize money of  1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners.

Solution.

Question 3.
Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.


(i) Are the number of spokes and the angles formed between the pairs of consecutive spokes in verse proportion?
(ii) Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.
(iii) How many spokes would be needed, if the angle between a pair of consecutive spokes is 40°?
Solution.
Let the angle (in degree) between a pair of consecutive spokes be \({ y }_{ 3 }\), \({ y }_{ 4 }\) and \({ y }_{ 5 }\) respectively. Then,

Question 4.
If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get, if the number of the children is reduced by 4?
Solution.
Suppose that each would get \({ y }_{ 2 }\) sweets.
Thus, we have the following table.

Question 5.
A farmer has enough food to feed 20 animals in his cattle for 6 days. How long would the food last if there were 10 more animals in his cattle?
Solution.
Suppose that the food would last for \({ y }_{ 2 }\) days. We have the following table:

Question 6.
A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If, he uses 4 persons instead of three, how long should they take to complete the job?
Solution.
Suppose that they take \({ y }_{ 2 }\) days to complete the job. We have the following table

Question 7.
A batch of bottles was packed in 25 boxes with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?

Solution.
Suppose that \({ y }_{ 2 }\) boxes would be filled. We have the following table:

Question 8.
A factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
Solution.
Suppose that \({ x }_{ 2 }\) machines would be required. We have the following table:

Question 9.
A car takes 2 hours to reach a destination by traveling at a speed of 60 km/h. How long will it take when the car travels at the speed of 80 km/h?
Solution.
Let it take \({ y }_{ 2 }\) hours. We have the following table:
sol.

Question 10.
Two persons could fit new windows in a house in 3 days.
(i) One of the persons fell ill before the work started. How long would the job take now?
(ii) How many persons would be needed to fit the windows in one day?
Solution.
(i) Let the job would take \({ y }_{ 2 }\) days. We have the following table:

Clearly, more the number of persons, lesser would be the number of days to do the job. So, the number of persons and number of days vary in inverse proportion.
So, 2 x 3 = 1 x \({ y }_{ 2 }\)
⇒ \({ y }_{ 2 }\) = 6
Thus, the job would now take 6 days.

(ii) Let \({ y }_{ 2 }\) persons be needed. We have the following table:

Clearly, more the number of persons, lesser would be the number of days to do the job. So, the number of persons and number of days vary in inverse proportion.
So, 3 x 2 = 1 x \({ y }_{ 3 }\)
⇒ \({ T }_{ 2 }\) = 6
Thus, 6 persons would be needed.

Question 11.
A school has 8periods a day each of 45 minutes duration. How long would each period be, if the school has 9 periods a day, assuming the number of school hours to be the same?
Solution.
Let each period be \({ y }_{ 2 }\) minutes long.
We have the following table:

We note that more the number of periods, lesser would be the length of each period. Therefore, this is a case of inverse proportion.
So, 8 x 45 = 9 x \({ y }_{ 2 }\)
⇒ \({ y }_{ 2 }=\frac { 8\times 45 }{ 9 } \)
⇒ \({ y }_{ 2 }\) = 40
Hence, each period would be 40 minutes long.

We hope the NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.2.

• Exponents and Powers Class 8 Ex 12.1

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 12
Chapter Name	Exponents and Powers
Exercise	Ex 12.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.2

Question 1.
Express the following numbers in standard form:
(i) 0.0000000000085
(ii) 0.00000000000942
(iii) 6020 000 000 000 000
(iv) 0.00000000837
(v) 31860000000
Solution.

Question 2.
Express the following numbers in usual form:

Solution.

Question 3.
Express the number appearing in the following statements in standard form:
(i) 1 micron is equal to \(\frac { 1 }{ 1000000 } \)m.
(ii) Charge of an electron is 0.000,000,000,000,000,000,16 coulomb.
(iii) Size of a bacteria is 0.0000005 m
(iv) Size of a plant cell is 0.00001275 m
(v) Thickness of a thick paper is 0.07 mm.
Solution.

Question 4.
In a stack there are 5 books each of thickness 20 mm and 5 paper sheets each of thickness 0.016 mm. What is the total thickness of the stack ?
Solution.
Total thickness of books
= 5 x 20 mm = 100 mm
Total thickness of paper sheets
= 5 x 0.016 mm = 0.080 mm
∴ Total thickness of the stack
= Total thickness of books + Total thickness of paper sheets
= 100 mm + 0.080 mm
= (100 + 0.080) mm
= 100.080 mm
= 1.0008 x \({ 10 }^{ 2 }\) mm.

We hope the NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.4.

• Mensuration Class 8 Ex 11.1
• Mensuration Class 8 Ex 11.2
• Mensuration Class 8 Ex 11.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 11
Chapter Name	Mensuration
Exercise	Ex 11.4
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.4

Question 1.
Given a cylindrical tank, in which situation will you find the surface area and in which situation volume?
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
Solution.
(a) Volume
(b) Surface area
(c) Volume.

Question 2.
The diameter of cylinder A is 7 cm, and the height is 14 cm. The diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has a greater surface area?

Solution.

Question 3.
Find the height of a cuboid whose base area is 180 \({ cm }^{ 2 }\) and volume is 900 \({ cm }^{ 3 }\).
Solution.
Height of the cuboid
= \(\frac { Volume\quad of\quad the\quad cuboid }{ Base\quad area\quad of\quad the\quad cuboid } \)
= \(\frac { 900 }{ 180 } \)
= 5 cm

Question 4.
A cuboid is of dimensions 60 cm x 54 cm x 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Solution.
A volume of the cuboid

Question 5.
Find the height of the cylinder whose volume is 1.54 \({ m }^{ 3 }\) and diameter of the base is 140 cm.
Solution.

Question 6.
A milk tank is in the form of a cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in liters that can be stored in the tank.
Solution.

Question 7.
If each edge of a cube is doubled,
(i) how many times will its surface area increase?
(ii) how many times will its volume increase?
Solution.
Let the original edge of the cube be a cm.
Then, its new edge = 2a cm

Question 8.
Water is pouring into a cuboidal reservoir at the rate of 60 liters per minute. If the volume of the reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.4 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.3.

• Visualising Solid Shapes Class 8 Ex 10.1
• Visualising Solid Shapes Class 8 Ex 10.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 10
Chapter Name	Visualising Solid Shapes
Exercise	Ex 10.3
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.3

Question 1.
Can a polyhedron have for its faces
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Solution.
(i) No
(ii) Yes
(iii) Yes

Question 2.
Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid).
Solution.
Possible, only if the number of faces is greater than or equal to 4.

Question 3.
Which are prisms among the following?


Solution.
We know that a prism is a polyhedron whose base and top faces are congruent and parallel and other (lateral) faces are parallelograms in shape. So, only (ii) and (iv) are prisms.

Question 4.
(i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Solution.
(i) The prisms and cylinder, both, have their base and top faces as congruent and parallel to each other. Also, a prism becomes a cylinder as the number of sides of its base becomes larger and larger.

(ii) The pyramids and cones are alike in the sense that their lateral faces meet at a point (called vertex). Also, a pyramid becomes a cone as the number of sides of its base becomes larger and larger.

Question 5.
Is a square prism same as a cube ? Explain.
Solution.
No; not always as it can be a cuboid also.

Question 6.
Verify Euler’s formula for these solids

Solution.
(i)
F = 7
V= 10
E = 15
F + V = 7 + 10 = 17
E + 2 = 15 + 2 = 17
So, F + V = E + 2
Hence, Euler’s Formula is verified,

(ii)
F = 9
V = 9
E = 16
F + V = 9 + 9 = 18
E + 2 = 16 + 2 = 18
So, F + V = E + 2
Hence, Euler’s Formula is verified

Question 7.
Using Euler’s formula find the unknown.

Solution.
(i)
F + V = E + 2
⇒ F + 6 = 12 + 2
⇒ F + 6 = 14
⇒ F = 14 – 6 = 8

(ii)
F + V = E + 2
⇒ 5 + V = 9 + 2
⇒ 5 + V = 11
⇒ V= 11-5 = 6

(iii)
F + V = E + 2
⇒ 20 + 12 = E + 2
⇒ 32 = E + 2
⇒ E = 32 – 2
⇒ E = 30

Question 8.
Can a polyhedron have 10 faces, 20 edges, and 15 vertices?
Solution.
Here F = 10
E = 20
V= 15
So, F + V = 10 + 15 = 25
E + 2 = 20 + 2 = 22
∵ F + V ≠ E + 2
∴ Such a polyhedron is not possible.

We hope the NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2.

• Visualising Solid Shapes Class 8 Ex 10.1
• Visualising Solid Shapes Class 8 Ex 10.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 10
Chapter Name	Visualising Solid Shapes
Exercise	Ex 10.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2

Question 1.
Look at the given map of a city.
Answer the following.
(a) Colour the map as follows: Bluewater, Red-fire station, Orange-Library, Yellow-schools, Green-Parks, Pink-Community Centre, Purple-Hospital, Brown-Cemetery.
(b) Mark a green X’ at the intersection of Road ‘C’ and Nehru Road, Green Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from Library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?

Solution.
(a) Please color yourself.
(b) See the above figure.
(c) See the above figure.
(d) City Park.
(e) Senior Secondary school.

Question 2.
Draw a map of your classroom using a proper scale and symbols for different objects.
Solution.
Please draw yourself.

Question 3.
Draw a map of your school compound using a proper scale and symbols for various features like playground main building, garden etc.
Solution.
Please draw yourself.

Question 4.
Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
Solution.
Please draw yourself.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5.

• Algebraic Expressions and Identities Class 8 Ex 9.1
• Algebraic Expressions and Identities Class 8 Ex 9.2
• Algebraic Expressions and Identities Class 8 Ex 9.3
• Algebraic Expressions and Identities Class 8 Ex 9.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	Algebraic Expressions and Identities
Exercise	Ex 9.5
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

Question 1.
Use a suitable identity to get each of the following products:


Solution.

Question 2.
Use the identity \((x+a)(x+b)={ x }^{ 2 }+(a+b)x+ab\) to find the following products:
(i) (x + 3) (x + 7)
(ii) (4x + 5) (4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) \((2{ a }^{ 2 }+9)(2{ a }^{ 2 }+5)\)
(vii) (xyz – 4) (xyz – 2).
Solution.

Question 3.
Find the following squares by using the identities.

Solution.

Question 4.
Simplify:

Solution.

Question 5.
Show that:

Solution.

Question 6.
Using identities, evaluate:

Solution.

Question 7.
Using \({ a }^{ 2 }-{ b }^{ 2 }=(a+b)(a-b)\), find

Solution.

Question 8.
Using \((x+a)(x+b)={ x }^{ 2 }+(a+b)x+ab\), find
(i) 103 x 104
(ii) 5.1 x 5.2
(iii) 103 x 98
(iv) 9.7 x 9.8
Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5, drop a comment below and we will get back to you at the earliest.