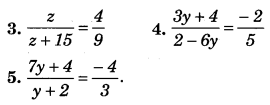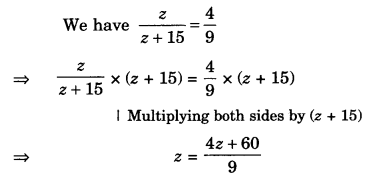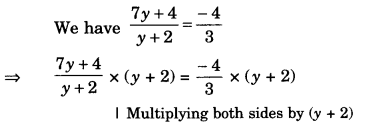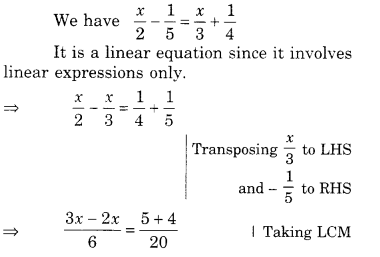NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.4.
- Practical Geometry Class 8 Ex 4.1
- Practical Geometry Class 8 Ex 4.2
- Practical Geometry Class 8 Ex 4.3
- Practical Geometry Class 8 Ex 4.5
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | Practical Geometry |
| Exercise | Ex 4.4 |
| Number of Questions Solved | 1 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.4
Question 1.
Construct the following quadrilaterals:
(i) Quadrilateral DEAR
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
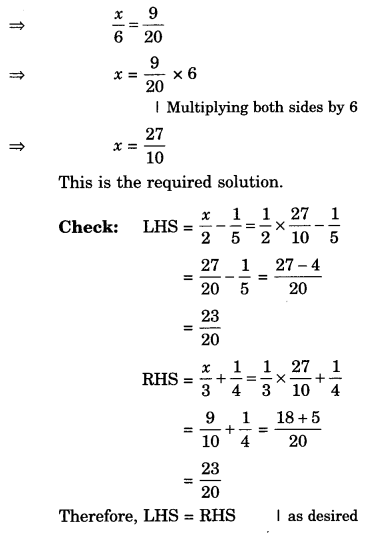
(ii) Quadrilateral TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 75°
∠U= 120°
Solution.
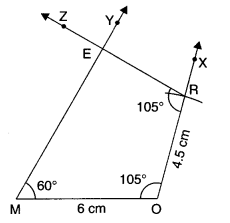
(i) Steps of Construction
- Draw DE = 4 cm.
- At E, draw ray EX such that ∠DEX = 60°.
- From ray EX, cut EA = 5 cm.
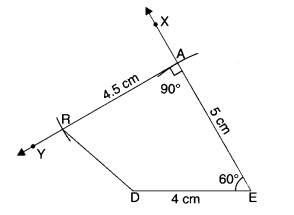
- At A, draw ray AY such that ∠EAY = 90°.
- Cut AR = 4.5 cm from ray AY.
- Join RD.
Then, DEAR is the required quadrilateral.
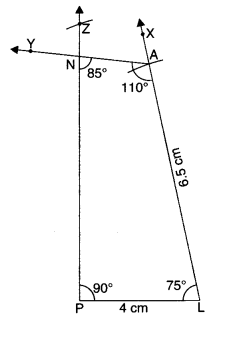
(ii) Steps of Construction
- Draw TR = 3.5 cm.
- At R, draw ray RX such that ∠TRX = 75°.
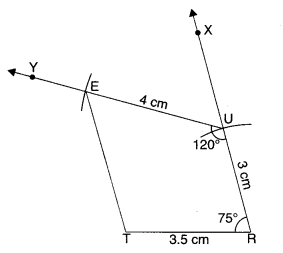
- Cut RU = 3 cm from ray RX.
- At U, draw ray UY such that ∠RUY = 120°.
- Cut UE = 4 cm from ray UY.
- Join ET.
Then, TRUE is the required quadrilateral.
We hope the NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.4 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.4, drop a comment below and we will get back to you at the earliest.