NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4.
- Squares and Square Roots Class 8 Ex 6.1
- Squares and Square Roots Class 8 Ex 6.2
- Squares and Square Roots Class 8 Ex 6.3
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | Squares and Square Roots |
| Exercise | Ex 6.4 |
| Number of Questions Solved | 9 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4
Question 1.
Find the square root of each of the following numbers by Division method:

Solution.
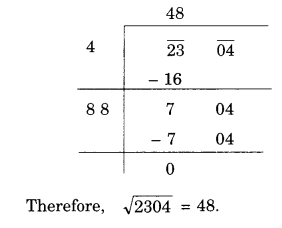
(i) 2304
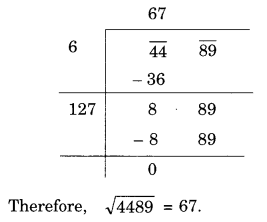
(ii) 4489
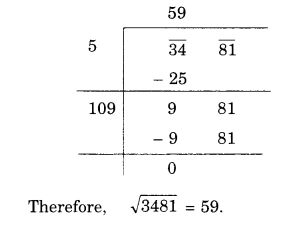
(iii) 3481
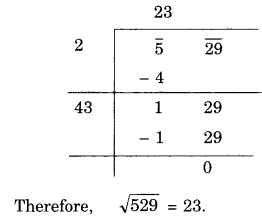
(iv) 529
(v) 3249
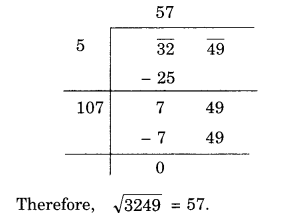
(vi) 1369
(vii) 5776
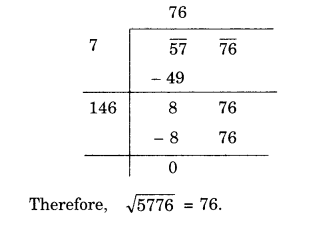
(viii) 7921
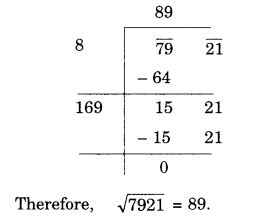
(ix) 576
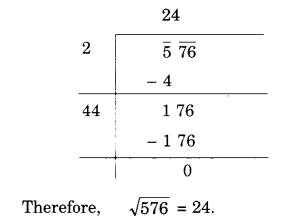
(x) 1024
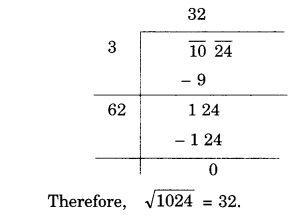
(xi) 3136
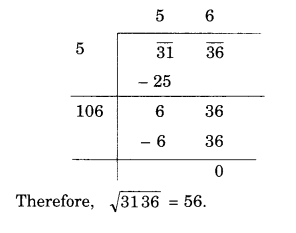
(xii) 900
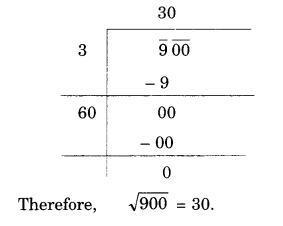
Question 2.
Find the number of digits in the square root of each of the following numbers (without any calculation):
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625.
Solution.
(i) 64
Number (n) of digits in 64 = 2 which is even.
∴ Number of digits in the square root of 64 \(\frac { n }{ 2 } =\frac { 2 }{ 2 } =1\)
(ii) 144
Number (n) of digits in 144 = 3 which is
∴ Number of digits in the square root of 144 \(\frac { n+1 }{ 2 } =\frac { 3+1 }{ 2 } =\frac { 4 }{ 2 } =2\)
(iii) 4489
Number (n) of digits in 4489 = 4 which is even.
∴ Number of digits in the square root of 4489 \(\frac { n }{ 2 } =\frac { 4 }{ 2 } =2\)
(iv) 27225
Number (n) of digits in 27225 = 5 which is odd.
∴ Number of digits in the square root of 27225 \(\frac { n+1 }{ 2 } =\frac { 5+1 }{ 2 } =\frac { 6 }{ 2 } =3\)
(v) 390625
Number (n) of digits in 390625 = 6 which is even.
∴ Number of digits in the square root of 390625 \(\frac { n }{ 2 } =\frac { 6 }{ 2 } =3\)
Question 3.
Find the square root of the following decimal numbers:
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Solution.
(i) 2.56

(ii) 7.29

(iii) 51.84
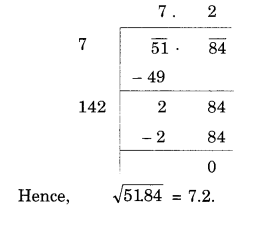
(iv) 42.25
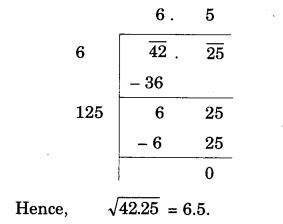
(v) 31.36
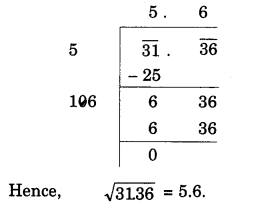
Question 4.
Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
Solution.
(i)402
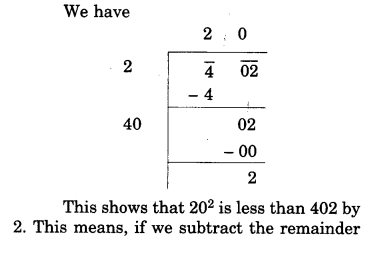
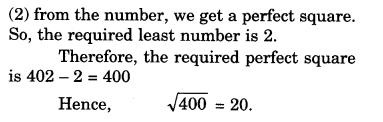
(ii) 1989

(iii) 3250

(iv) 825

(v) 4000

Question 5.
Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525
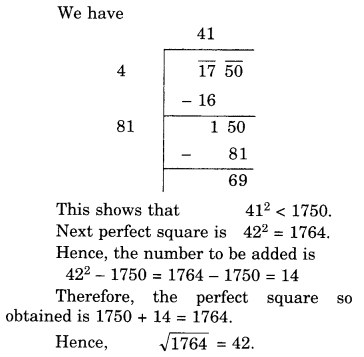
(ii) 1750
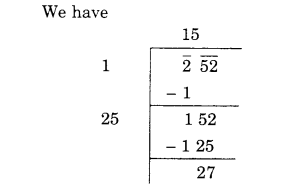
(iii) 252
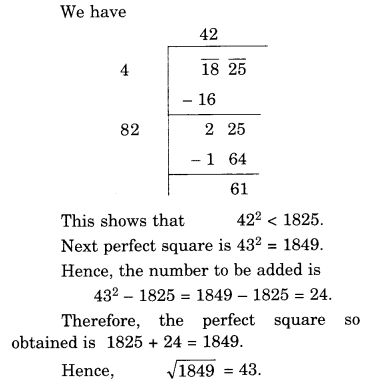
(iv) 1825
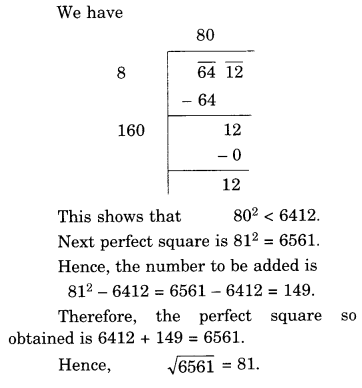
(v) 6412
Solution.
(i) 525

(ii) 1750
(iii) 252

(iv) 1825
(v) 6412
Question 6.
Find the length of the side of a square whose area is 441 \({ m }^{ 2 }\).
Solution.
Area of the square = 441 \({ m }^{ 2 }\)
∴ Length of the side of the square
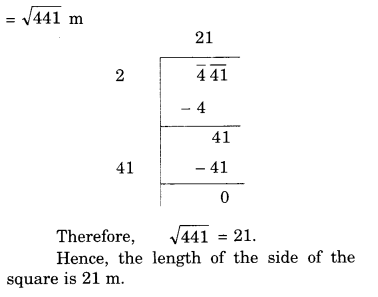
Question 7.
In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC
(b) If AC 13 cm, BC = 5 cm, find AB.
Solution.
(a) In the right triangle ABC,
∠B = 90°
Given
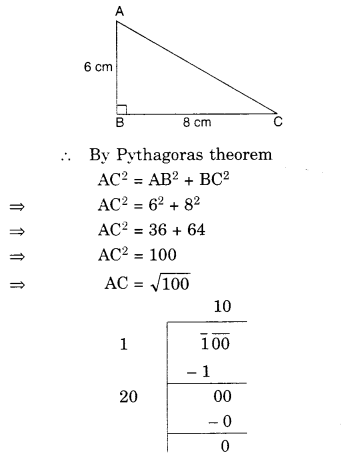
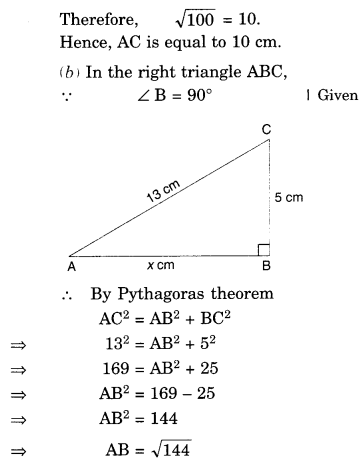

Question 8.
A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this.
Solution.
Let the number of rows be x.
Then the number of columns is x.

Question 9.
There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement?
Solution.
Let the number of rows be x.
Then the number of columns is x.

We hope the NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4 are part help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4 are part, drop a comment below and we will get back to you at the earliest.