NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2.

• Cubes and Cube Roots Class 8 Ex 7.1

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 7
Chapter Name	Cubes and Cube Roots
Exercise	Ex 7.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2

Question 1.
Find the cube root of each of the following numbers by prime factorisation method:
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Solution.
(i) 64

(ii) 512

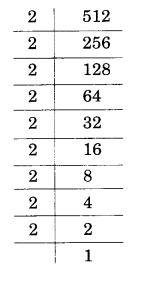
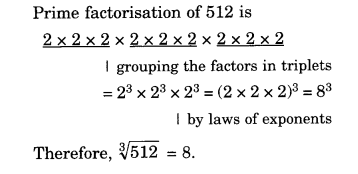
(iii) 10648

(iv) 27000

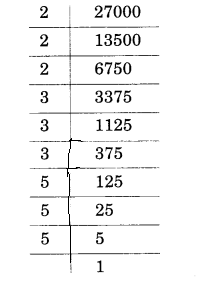
(v) 15625

(vi) 13824

(vii) 110592

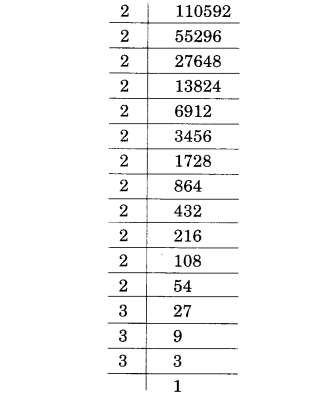
(viii) 46656

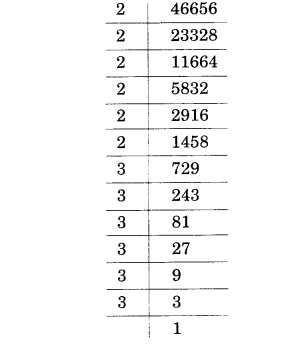
(ix) 175616

(x) 91125

Question 2.
State true or false:
(i) Cube of any odd number is even,
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution.
(i) False
(ii) True
(iii) False ⇒ \({ 15 }^{ 2 }\) = 225, \({ 15 }^{ 3 }\) = 3375
(iv) False ⇒ \({ 12 }^{ 3 }\) = 1728
(v) False ⇒ \({ 10 }^{ 3 }\) = 1000, \({ 99 }^{ 3 }\) = 970299
(vi) False ⇒ \({ 10 }^{ 3 }\) = 1000, \({ 99 }^{ 3 }\) = 970299
(vii) True ⇒ \({ 1 }^{ 3 }\) = 1; \({ 2 }^{ 3 }\) = 8

Question 3.
You are told that 1,331 is a perfect cube. Can you guess without factorization what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Solution.
By guess,
Cube root of 1331 =11
Similarly,
Cube root of 4913 = 17
Cube root of 12167 = 23
Cube root of 32768 = 32
EXPLANATIONS
(i)
Cube root of 1331
The given number is 1331.

Step 1. Form groups of three starting from the rightmost digit of 1331. 1 331
In this case, one group i.e., 331 has three digits whereas 1 has only 1 digit.
Step 2. Take 331.
The digit 1 is at one’s place. We take the one’s place of the required cube root as 1.
Step 3. Take the other group, i.e., 1. Cube of 1 is 1.
Take 1 as ten’s place of the cube root of 1331.
Thus, \(\sqrt [ 3 ]{ 1331 } =11\)

(ii)
Cube root of 4913
The given number is 4913.

Step 1. Form groups of three starting from the rightmost digit of 4913.
In this case one group, i.e., 913 has three digits whereas 4 has only one digit.
Step 2. Take 913.
The digit 3 is at its one’s place. We take the one’s place of the required cube root as 7.
Step 3. Take the other group, i.e., 4. Cube of 1 is 1 and cube of 2 is 8. 4 lies between 1 and 8.
The smaller number among 1 and 2 is 1.
The one’s place of 1 is 1 itself. Take 1 as ten’s place of the cube root of 4913.
Thus, \(\sqrt [ 3 ]{ 4913 } =17\)

(iii)
Cube root of 12167
The given number is 12167.

Step 1. Form groups of three starting from the rightmost digit of 12167.
12 167. In this case, one group, i. e., 167 has three digits whereas 12 has only two digits.
Step 2. Take 167.
The digit 7 is at its one’s place. We take the one’s place of the required cube root as 3.
Step 3. Take the other group, i.e., 12. Cube of 2 is 8 and cube of 3 is 27. 12 lies between 8 and 27. The smaller among 2 and 3 is 2.
The one’s place of 2 is 2 itself. Take 2 as ten’s place of the cube root of 12167.
Thus, A/12167 = 23.
Thus, \(\sqrt [ 3 ]{ 12167 } =23\).

(iv)
Cube root of 32768
The given number is 32768.

Step 1. Form groups of three starting from the rightmost digit of 32768.
32 768. In this case one group,
i. e., 768 has three digits whereas 32 has only two digits.
Step 2. Take 768.
The digit 8 is at its one’s place. We take the one’s place of the required cube root as 2.
Step 3. Take the other group, i.e., 32.
Cube of 3 is 27 and cube of 4 is 64.
32 lies between 27 and 64.
The smaller number between 3 and 4 is 3.
The ones place of 3 is 3 itself. Take 3 as ten’s place of the cube root of 32768.
Thus, \(\sqrt [ 3 ]{ 32768 } =32\).

 

We hope the NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2, drop a comment below and we will get back to you at the earliest.