NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 8 |
| Chapter Name | Comparing Quantities |
| Exercise | Ex 8.1 |
| Number of Questions Solved | 6 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1
Question 1.
Find ratio of the following:
(a) Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
(b) 5 m to 10 km
(c) 50 paise ₹ 5
Solution.
(a)
Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour
Ratio of the speed of cycle which is 15 km per hour to the speed of scooter which is 30 km per hour
= 15 km per hour : 30 km per hour = 15 : 30
= \(\frac { 15 }{ 30 } =\frac { 1 }{ 2 } \) or 1 : 2
(b)
5 m to 10 km
10 km = 10 x 1000 m = 10000 m
∴ Ratio of 5 m to 10 km
= 5 m : 10 km
= 5 m : 10000 m
= 5 : 10000
= \(\frac { 5 }{ 10000 } =\frac { 1 }{ 2000 } \) or 1 : 2000
(c)
50 paise to ₹ 5
₹ 5 = 5 x 100 = 500 paise
∴ Ratio of 50 paise to ₹ 5
= 50 paise : ₹ 5
= 50 paise : 500 paise
= 50 : 500
= \(\frac { 50 }{ 500 } =\frac { 1 }{ 10 } \) or 1 : 10
Question 2.
Convert the following ratios to percentages:
(a) 3: 4
(b) 2 : 3
Solution.
(a) 3: 4

(b) 2 : 3
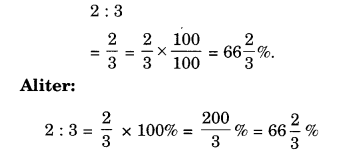
Question 3.
72% of 25 students are good in mathematics. How many are not good in Mathematics?
Solution.
Total number of students = 25
Students good in mathematics = 72%
∴ Students who are not good in mathematics
= (100 – 72)% = 28%
∴ Number of those students who are not good in mathematics
= 28% of 25
= \(\frac { 28 }{ 100 } \times 25=7\)
Hence, 7 students are not good in mathematics.
Question 4.
A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?
Solution.
∵ If 40 matches were won, then the total number of matches played = 100
∴ If 1 match was won, then the total number of matches played = \(\frac { 100 }{ 40 } \)
∴ If 10 matches were won, then the total number of matches played = \(\frac { 100 }{ 40 } \times 10=25\)
Hence, they played 25 matches in all.
Aliter: According to the question, 40% of (total number of matches) = 10
⇒ \(\frac { 40 }{ 100 } \) x (total number of matches) = 10
⇒ Total number of matches = \(\frac { 10\times 100 }{ 40 } \) = 25
Hence, they played 25 matches in all.
Question 5.
If Chameli had ₹ 600 left after spending 75% of her money, how much did she have in the beginning?
Solution.
Percentage of money left = (100 – 75)% = 25%
∵ If Chameli had ₹ 25 left, then the money she had in the beginning = 100
∴ If Chameli had ₹ 1 left, then the money she had in the beginning = \(\frac { 100 }{ 25 } \)
∴ If Chameli has ₹ 600 left, then the money she had in the beginning = \(\frac { 100 }{ 25 } \times 600=2400\)
Hence, the money she had in the beginning was ₹ 2400.
Aliter:
According to the question, 25% of total money = ₹ 600
⇒ \(\frac { 25 }{ 100 } \) x total money = ₹ 600
⇒ Total money = ₹ \(\frac { 600\times 100 }{ 25 } \) = ₹ 2400
Hence, the money she had in the beginning was ₹ 2400
Question 6.
If 60% of people in a city like a cricket, 30% like football and the remaining like other games then what percent of the people like other games? If the total number of people are 50 lakh, find the exact number who like each type of game.
Solution.
People who like other games = [100 – (60 + 30)]%
= (100 – 90)% = 10%.
Total number of people = 50 lakh
= 5000000
∴ Number of people who like cricket = 60% of 5000000
= 5000000 x \(\frac { 60 }{ 100 } \)
= 3000000 = 30 lakh
Number of people who like football = 30% of 5000000
= 5000000 x \(\frac { 30 }{ 100 } \)
= 1500000 = 15 lakh
Number of people who like the other games
= 10% of 5000000
= 5000000 x \(\frac { 10 }{ 100 } \)
= 5,00,000 = 5 lakh
We hope the NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1, drop a comment below and we will get back to you at the earliest.