NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.3 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.3.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | Triangles |
| Exercise | Ex 5.3 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.3
Question 1.
∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that
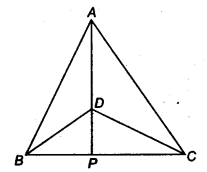
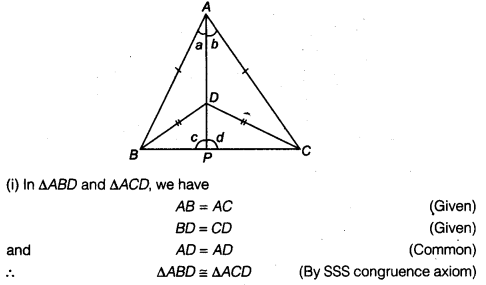
(i) ∆ABD = ∆ACD
(ii) ∆ABP = ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Solution:
Given ∆ABC and ∆DBC are two isosceles triangles having common
base BC, suchthat AB=AC and DB=OC.
To prove:
(i) ∆ABD = ∆ACD
(ii) ∆ABP = ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.

Question 2.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A
Solution:
In ∆ ABD and ∆ ACD, we have
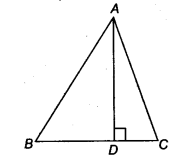
AB = AC (Given)
∠ADB = ∠ADC = 90° (∵ Given AD ⊥BC)
AD = AD (Common)
∴ ∆ ABD ≅ ∆ ACD (By RHS congruence axiom)
BD=DC (By CPCT)
⇒ AD bisects BC.
∠ BAD = ∠ CAD (By CPCT)
∴ AD bisects ∠A .
Question 3.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and OR and median PN of ∆PQR (see figure). Show that
(i) ∆ABC ≅ ∆PQR
(ii) ∆ABM ≅ ∆PQN
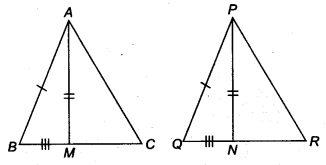
Solution:

Question 4.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:
In ∆BEC and ∆CFB, we have
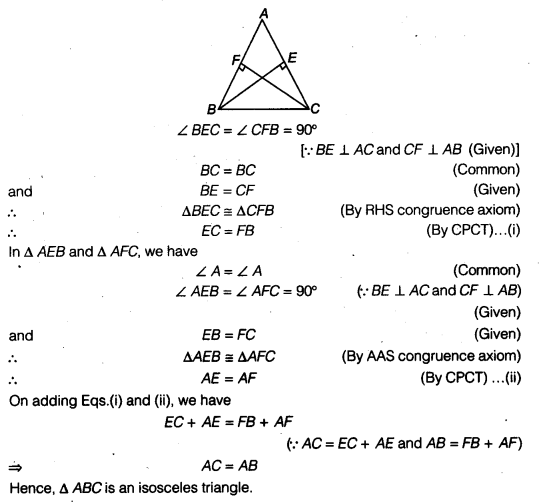
Question 5.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution:
In ∆ABP and ∆ACP, We have
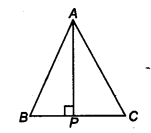
AB = AC (Given)
AP = AP (Common)
and ∠APB = ∠APC = 90° (∵ AP ⊥ BC)
∴ ∆ABP ≅ ∆ACP (By RHS congruence axiom)
⇒ ∠B = ∠C (By CPCT)
We hope the NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.3 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.3, drop a comment below and we will get back to you at the earliest.