RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1

RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios MCQS

Question 1.
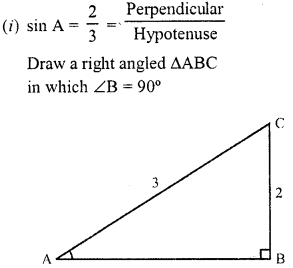
In each of the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.

Solution:
∴ Perpendicular BC – 2 units and
Hypotenuse AC = 3 units
By Phythagoras Theorem, in AABC,
(Hypotenuse)² = (Base)² + (Perpendicular)²
AC² = AB² + BC²
⇒ (3)² = (AB)² + (2)²
⇒ 9 = AB² + 4 ⇒ AB² = 9-4 = 5
AB = √5 units

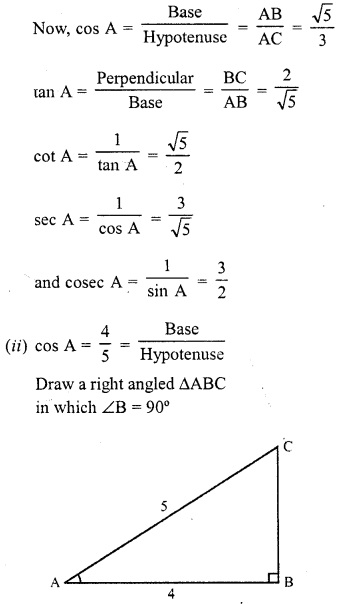
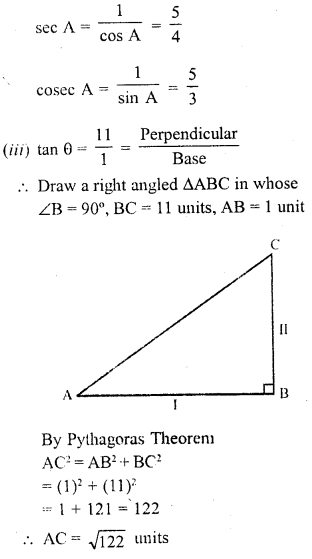
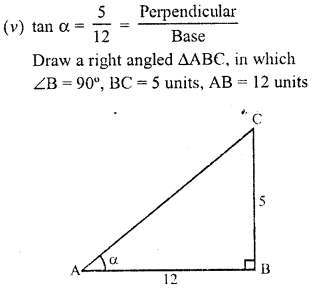
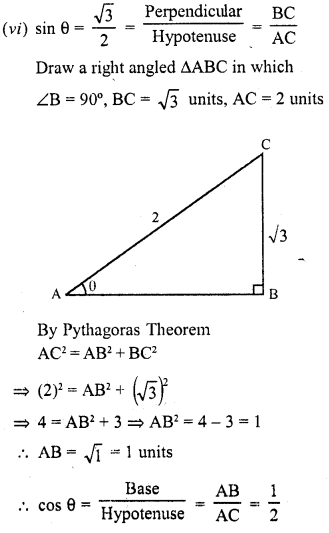
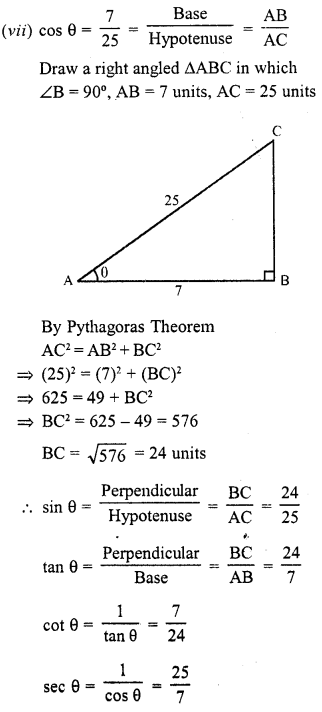
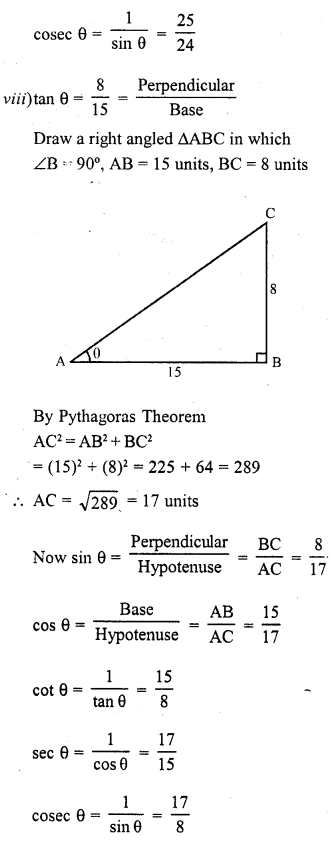
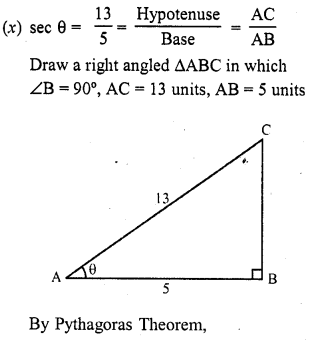
Question 2.
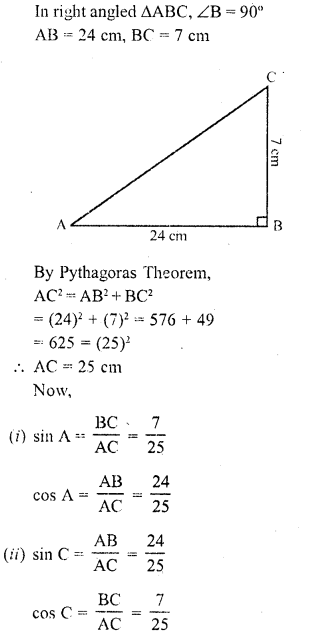
In a ΔABC, right angled at B, AB = 24 cm, BC = 7 cm. Determine
(i) sin A, cos A
(ii) sin C, cos C.
Solution:

Question 3.
In the figure, find tan P and cot R. Is tan P = cot R ?

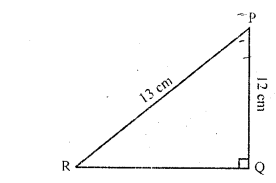
Solution:

Question 4.
If sin A = \(\frac { 9 }{ 41 }\), compute cos A and tan A.
Solution:

Question 5.
Given 15 cot A = 8, find sin A and sec A.
Solution:

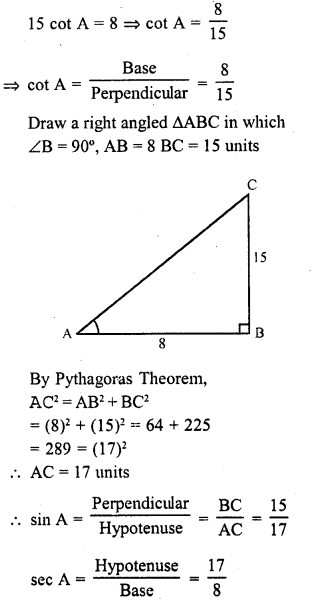
Question 6.
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
Solution:

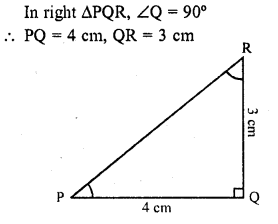
Question 7.
If cot 0 = \(\frac { 7 }{ 8 }\), evaluate :

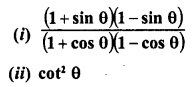
Solution:

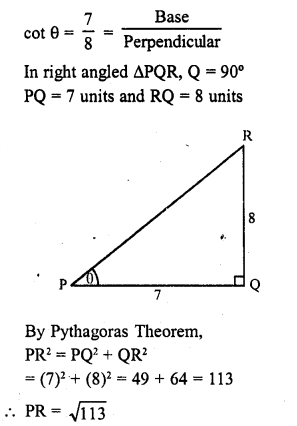
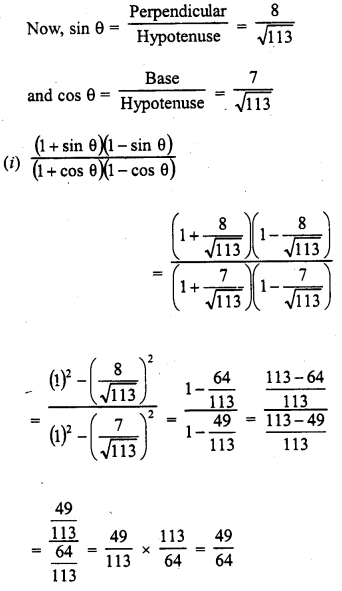
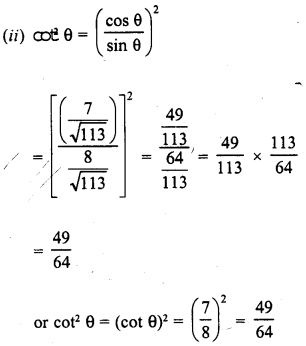
Question 8.
If 3 cot A = 4, check whether \(\frac { 1-{ tan }^{ 2 }A }{ 1+{ tan }^{ 2 }A }\) = cos² A – sin² A or not.
Solution:

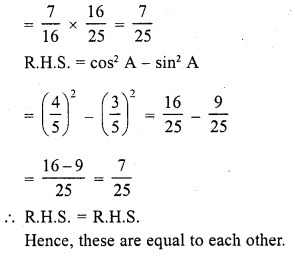
Question 9.
If tan θ = a/b , Find the Value of \(\frac { cos\theta +sin\theta }{ cos\theta -sin\theta }\).
Solution:

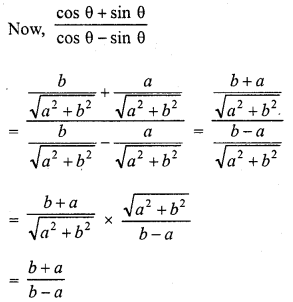
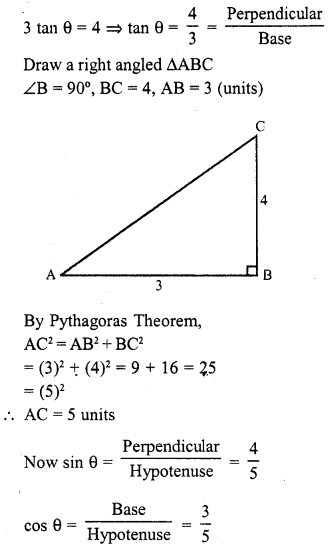
Question 10.
If 3 tan θ = 4, find the value of 4cos θ – sin θ \(\frac { 4cos\theta -sin\theta }{ 2cos\theta +sin\theta }\).
Solution:

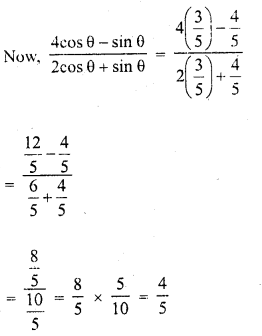
Question 11.
If 3 cot 0 = 2, find the value of \(\frac { 4sins\theta -3cos\theta }{ 2sin\theta +6cos\theta }\).
Solution:

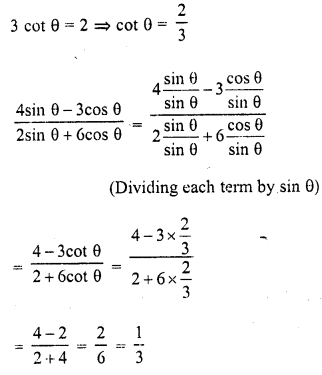
Question 12.
If tan θ = \(\frac { a }{ b }\), prove that

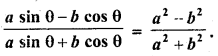
Solution:

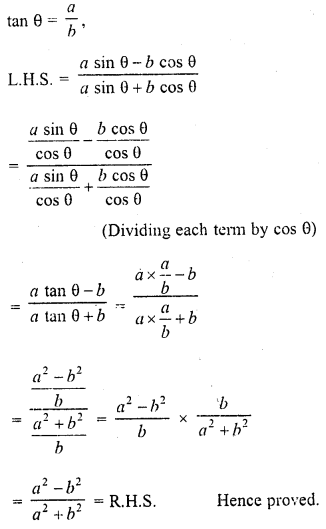
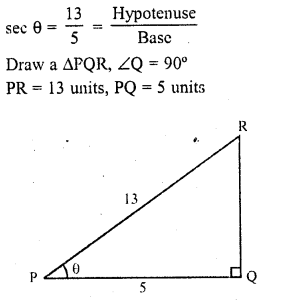
Question 13.
If sec θ = \(\frac { 13 }{ 5 }\), show that \(\frac { 2sins\theta -3cos\theta }{ 4sin\theta -9cos\theta }\) =3.
Solution:

Question 14.
If cos θ \(\frac { 12 }{ 13 }\), show that sin θ (1 – tan θ) \(\frac { 35 }{ 156 }\).
Solution:

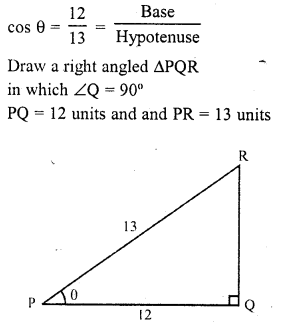
Question 15.

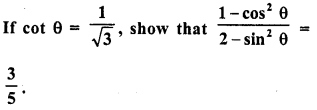
Solution:

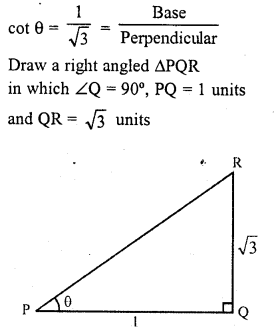
Question 16.

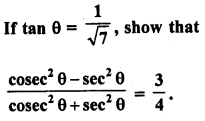
Solution:

Question 17.
If sec θ = \(\frac { 5 }{ 4 }\), find the value of \(\frac { sins\theta -2cos\theta }{ tan\theta -cot\theta }\).
Solution:

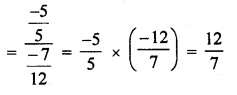
Question 18.

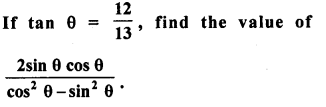
Solution:

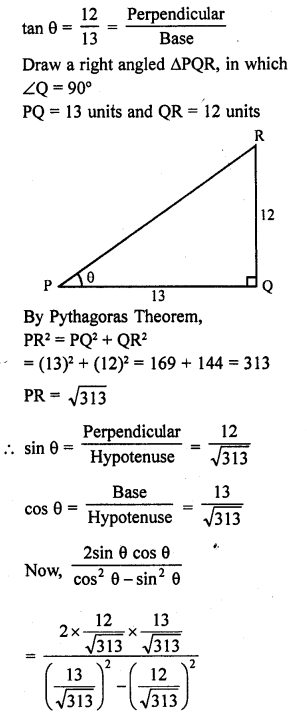
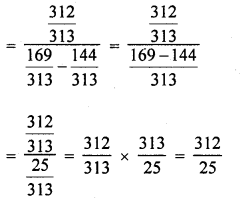
Question 19.

Solution:

Question 20.

Solution:

Question 21.
If tan θ = \(\frac { 24 }{ 7 }\), find that sin θ + cos θ.
Solution:

Question 22.
If sin θ = \(\frac { a }{ b }\), find sec θ + tan θ in terms of a and b.
Solution:

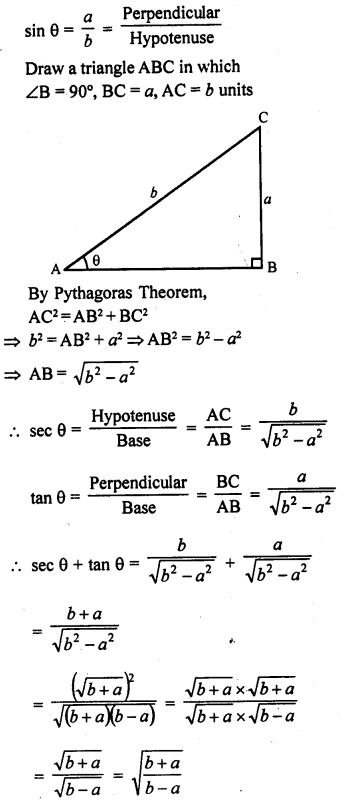
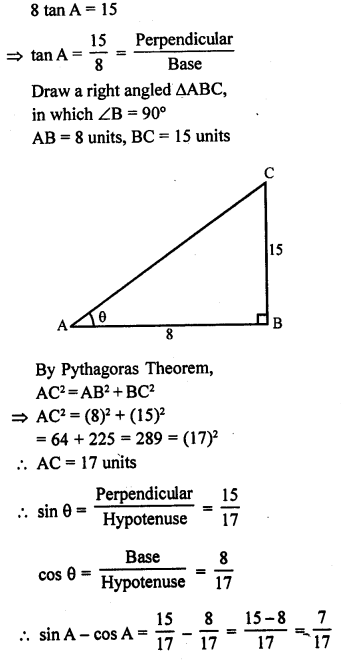
Question 23.
If 8 tan A = 15, find sin A – cos A.
Solution:

Question 24.

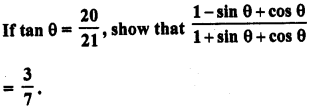
Solution:

Question 25.

Solution:

Question 26.
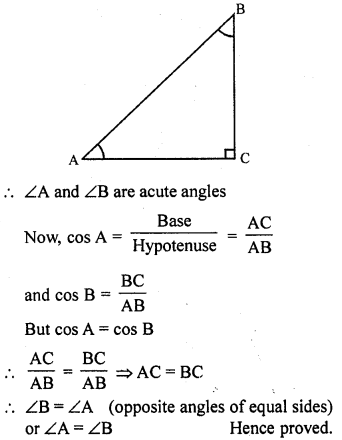
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
∠A and ∠B are acute angles and cos A = cos B
Draw a right angle AABC, in which ∠C – 90°

Question 27.
In a ∆ABC, right angled at A, if tan C =√3 , find the value of sin B cos C + cos B sin C. (C.B.S.E. 2008)
Solution:

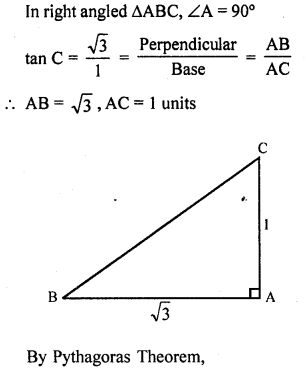
Question 28.
28. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = \(\frac { 12 }{ 5 }\) for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = \(\frac { 4 }{ 3 }\) for some angle θ.
Solution:
(i) False, value of tan A 0 to infinity.
(ii) True.
(iii) False, cos A is the abbreviation of cosine A.
(iv) False, it is the cotengent of angle A.
(v) Flase, value of sin θ varies on 0 to 1.

Question 29.

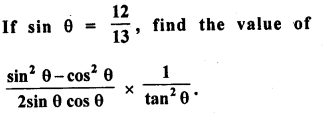
Solution:

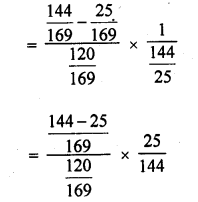
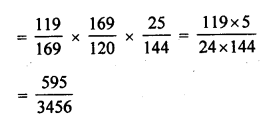
Question 30.

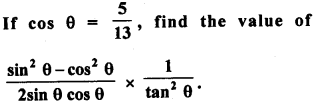
Solution:

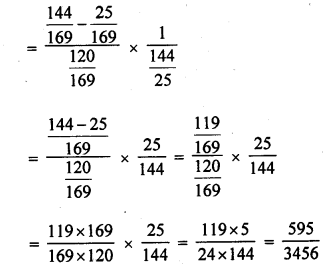
Question 31.

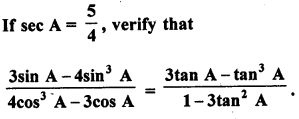
Solution:

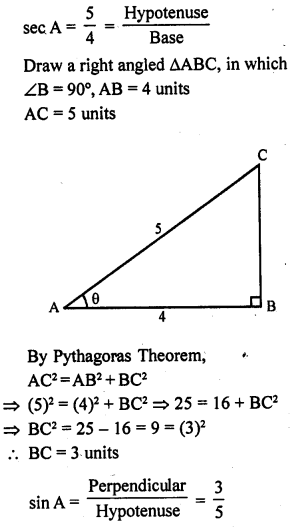
Question 32.
If sin θ =\(\frac { 3 }{ 4 }\), prove that

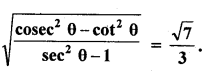
Solution:

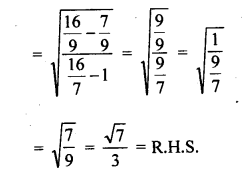
Question 33.

Solution:

Question 34.

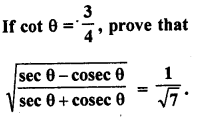
Solution:

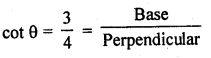
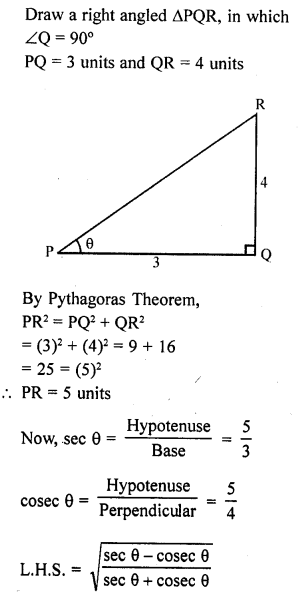
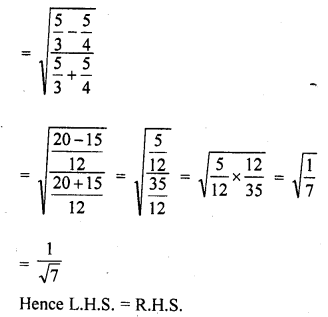
Question 35.
If 3 cos θ-4 sin θ = 2 cos θ + sin θ, find tan θ.
Solution:

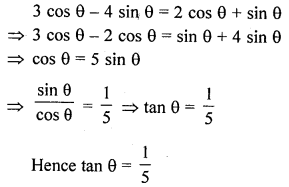
Question 36.
If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
Solution:
∠A and ∠P are acute angles and tan A = tan P Draw a right angled AAPB in which ∠B = 90°

 

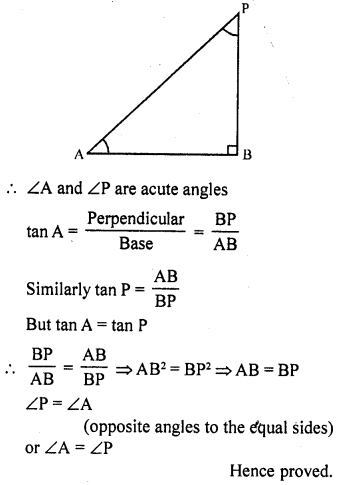
Hope given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.