RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS

Question 1.
A bucket has top and bottom diameters of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of ?1.20 per dm2. (Use % = 3.14)
Solution:
Upper diameter = 40 cm
and lower diameter = 20 cm
∴  Upper radius (r₁) = \((\frac { 40 }{ 2 } )\) = 20 cm
and lower radius (r₂) = \((\frac { 20 }{ 2 } )\) = 10 cm
Depth or height (h) = 12 cm
Volume of the bucket

Question 2.
A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm, and height 3 cm. Find the area of its whole surface and volume.
Solution:
Base diameter of frustum = 20 cm 20
∴  Radius (r₁) = \((\frac { 20 }{ 2 } )\) = 10 cm
and diameter of top = 12 cm

Question 3.
The slant height of the frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface of the frustum.
Solution:
Perimeter of the top of frustum = 18 cm

Question 4.
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
Solution:
Perimeter of the top of frustum = 44 cm

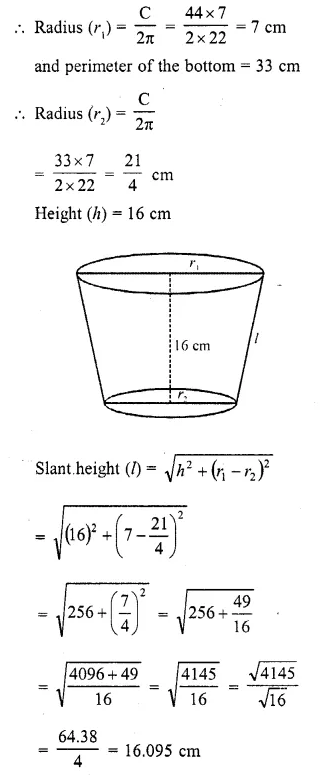
Question 5.
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7). (C.B.S.E. 2000)
Solution:

Question 6.
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be \((\frac { 1 }{ 125 } )\)  of the volume of the original cone, determine at what height above the base the section is made.
Solution:
Total height of the cone (h₁) = 20 cm
Let a cone whose height is h₂ is cut off Then height of the remaining portion (frustum)

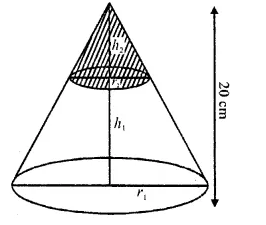
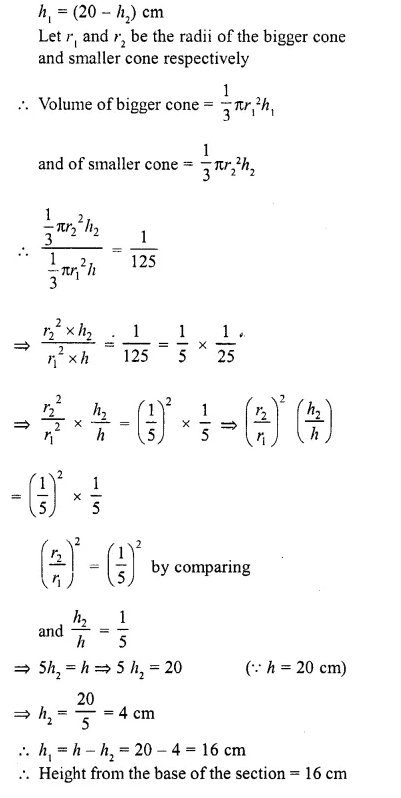
Question 7.
If the radii of the circular ends of a bucket 24 cm high are 5 cm and 15 cm respectively, find the surface area of the bucket.
Solution:
Height of the bucket (frustum) (A) = 24 cm
Radius of the top (r₁) = 15 cm 1
and radius of the bottom (r₂) = 5 cm

Question 8.
The radii of the circular bases of a frustum of a right circular cone are 12 cm and 3 cm and the height is 12 cm. Find the total surface area and the volume of the frustum.
Solution:
Height of the frustum (A) = 12 cm
Radius of the top (r₁) = 12 cm
and radius of the bottom (r₂) = 3 cm

Question 9.
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m, the height of the frutum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
Solution:
Radius of the bottom of the tent (r₁) = 13 m
and radius of the top (r₂) = 7 m
Height of frustum portion (h₁) = 8 m
Slant height of the conical cap (l₂) = 12 m
Let l₁ be the slant height of the frustum portion, then

Question 10.
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of ₹44 per litre which the container can hold. [NCERT Exemplar]
Solution:
Given that, height of milk container (h) = 16 cm
Radius of lower end of milk container (r) = 8 cm
and radius of upper end of milk container (R) = 20 cm

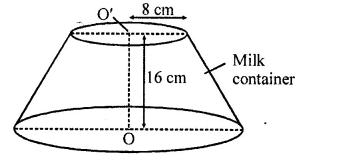
∴ Volume of the milk container made of metal sheet in the form of a frustum of a cone

Question 11.
A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container, at the rate of ₹25 per litre. (Use π = 3.14) [NCERT Exemplar]
Solution:

Question 12.
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm³ of water. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. (Use π = 3.14). [CBSE 2006C]
Solution:
Volume of frustum (bucket) = 12308.8 cm³
Upper radius (r₁) = 20 cm
and lower radius (r₂) = 12 cm

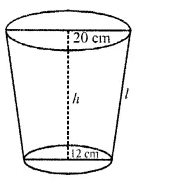
Question 13.
A bucket made of aluminium sheet is of height 20 cm and its upper and lower ends are of radius 25 cm and 10 cm respectively. Find the cost of making the bucket if the aluminium sheet costs Rs. 70 per 100 cm². (Use π = 3.14) (C.B.S.E. 2006C)
Solution:
Height of bucket (frustum) (h) = 20 cm
Upper radius (r₁) = 25 cm
and lower radius (r₂) = 10

Question 14.
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area. (C.B.S.E. 2005)
Solution:
Upper radius of frustum (r₁) = 3.3 cm
and lower radius (r₂) = 27 cm
Slant height (l) = 10 cm

Question 15.
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm respectively. Find the volume of the bucket. Also, find the cost of the bucket if the cost of metal sheet used is Rs. 20 per 100 cm². (Use π = 3.14) (CBSE 2008)
Solution:
Lower radius of bucket (r) = \((\frac { 16 }{ 2 } )\) = 8 cm
and upper radius (R) = \((\frac { 40 }{ 2 } )\) = 20 cm
Height (h) = 16

Question 16.
A solid is in the shape of a frustum of a cone. The diameter of the two circular ends are 60 cm and 36 cm and the leight is 9 ³cm. Find the area of its whole surface and the volume. [CBSE 2010]
Solution:
In a solid frustum upper diameter = 60 cm
∴ Radius (r₁) = \((\frac { 60 }{ 2 } )\) = 30 cm
Lower diameter = 36 cm 36
∴ Radius (r₂) = \((\frac { 36 }{ 2 } )\) = 18 cm
Height (h) = 9 cm

Question 17.
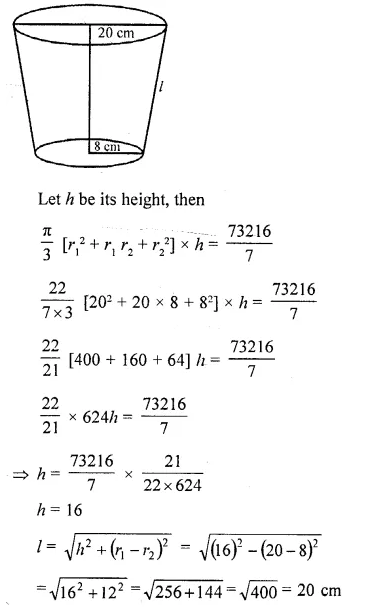
A milk container is made of metal sheet in the shape of frustum of a cone whose volucrn is 10459\((\frac { 3 }{ 7 } )\) cm³. The radii of its lower and upper circular ends are 8 cm and 20 cm respectively. Find the cost of metal sheet used in making the container at the rate of Rs. 1.40 per cm². (Use π = 22.7) [CBSE 2010]
Solution:
Volume of frustum = 10459\((\frac { 3 }{ 7 } )\) cm3 73216
= \((\frac { 73216 }{ 7 } )\) cm³
Lower radius (r₂) = 8 cm
and upper radius (r₁) = 20 cm

Question 18.
A solid cone of base radius 10 cm is cut into two parts through the mid-pint of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone. [CBSE 2013]
Solution:
Radius of solid cone (r) = 10 cm
Let total height = h
In ΔAOB,
C is mid point of AO and CD || OB

Question 19.
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of ₹10 per 100 cm². (Use π = 3.14). [CBSE 2013]
Solution:

Question 20.
In the given figure, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use π = 22/7 and \(\sqrt { 5 } \) = 2.236).  [ CBSE 2015]

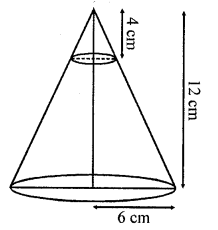
Solution:
Total height of cone = 12 cm
Radius of its base = 6 cm
A cone of height 4 cm is cut out
Height of the so formed frustum = 12 – 4 = 8 cm
Let r be the radius of the cone cut out

Question 21.
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
Solution:
Let the height and radius of the given cone be H and R respectively.
The cone is divided into two parts by drawing a plane through the mid point of its axis and parallel to the base.
Upper part is a smaller cone and the bottom part is the frustum of the cone.

Question 22.
A bucket, made of metal sheet, is in the form of a cone whose height is 35 cm and radii of circular ends are 30 cm and 12 cm. How many litres of milk it contains if it is full to the brim? If the milk is sold at ₹40 per litre, find the amount received by the person. [CBSE 2017]
Solution:
Radii of the bucket in the form of frustum of cone = 30 cm
and 12 cm Depth of the bucket = 35 cm

Question 23.
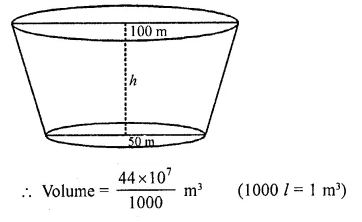
A reservoir in the form of the frustum of a right circular cone contains 44 x 10⁷ litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take : π = 22/7)
Solution:
A reservoir is a frustum in shape and its upper radius (r₁) = 100 m
Lower radius (r₂) = 50 m
and capacity of water in it = 44 x 10⁷ litres

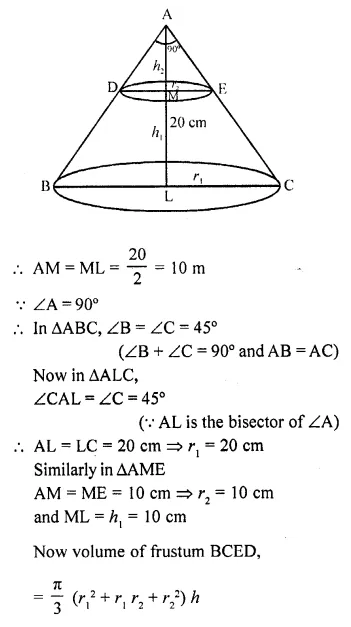
P.Q. A metallic right circular cone 20 cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to the base. If the frustum so obtained be drawn into a wire  \((\frac { 1 }{ 16 } )\)cm, find the length of the wire.

Solution: In the cone ABC, ∠A = 90°, AL ⊥ BC and = 20 cm
It is cut into two parts at the middle point M on the axis AL
AL bisects ∠A also

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.